一种再制造系统多目标缓冲区分配方法与流程

本发明属于机械再制造技术领域，涉及再制造系统缓冲区分配方法，尤其涉及一种再制造系统多目标缓冲区分配方法。

背景技术：

制造业是国民经济的主体，是立国之本、兴国之器、强国之基。在过去的一个世纪，制造业在为人类带来了前所未有的财富的同时，也消耗了大量的能源、资源并且成为污染环境的重要源头。因此，再制造应运而生。再制造是把到达使用寿命或即将被抛弃的产品通过修复和技术改造使其达到甚至超过原型产品性能的加工过程。再制造是物质循环利用的有效途径，是循环经济中再利用原则的具体体现，充分体现出了节能减排和环境友好的理念。

与传统制造系统不同的是，由于回收产品质量的不确定性，再制造系统的生产过程存在一系列的不确定性，导致再制造系统的生产运营管理更加复杂，对系统的性能优化提出了更高要求。生产过程具有以下类型的不确定性：回收产品到达时间和数量不确定、回收产品可再制造率的不确定、回收产品再制造时间加工时间的不确定、回收产品再制造加工工序的不确定、回收产品再制造数量和市场需求的不确定。

为实现生产利润的最大化，需要考虑回收产品的数量与再制造产品需求数量的平衡。因此，在生产管理上需要对回收产品的库存量和市场需求进行平衡。

在制造系统中，缓冲区是为保证生产线尽可能地处于流动状态而设置的，用来放置工件的存储区域。尽管缓冲区可以有效缓解不确定性对系统的冲击，但设定缓冲区需要额外的资金和空间投入、成本较高。因此，缓冲区看作整体时，如何使一定数量的缓冲区容量发挥最大效用，该问题被称为缓冲区分配问题。

目前，对再制造系统的缓冲区分配研究的文献并不多。Aksoy和Gupta首次以再制造系统为对象，选取再制造成本为目标，研究缓冲区分配问题。假设缓冲区有限且机器不可靠，利用排队论-分解-扩展方法求解系统性能，并提出一种近似缓冲区分配优化方法(Near Optimal Buffer Allocation Plan，NOBAP)。实验结果证明：NOBAP方法的性能具有很好的一贯性、鲁棒性和寻优性。Su在Aksoy和Gupta研究的基础上，采用质量分级将回收件分为高、低两个等级并规定高等级的回收件可以优先加工，实验证明：质量分级和设立优先级可以显著提高系统性能。但以上研究中未考虑进“返工”、“舍弃”、故障对缓冲区分配的影响，并且选择成本作为单个目标，无法直观观察到缓冲区配置对系统性能的影响。此外，NOBAP方法在优化缓冲区配置时，需要利用系统状态数据，尽管寻优效果良好但耗时较长。

当前缓冲区分配问题的研究有三大研究方向：(1)多目标缓冲区分配；(2)混合求解算法；(3)决策支持系统。这三大方向分别对应于缓冲区分配问题的三大解决要点：(1)更加全面直观地表现出系统性能；(2)更加快速、有效、鲁棒、适应性强地求解缓冲区容量分配这一NP-hard问题；(3)更加有力地推进缓冲区分配方法的实际应用。

技术实现要素：

发明目的：本发明提供一种再制造系统多目标缓冲区分配方法，可以解决再制造系统多目标缓冲区分配的问题，在收敛性、多样性以及运行时间方面效果良好。

技术方案：(1)建立再制造系统模型，所述再制造系统模型包括再制造生产线、库存及缓冲区，设再制造生产线包括M个工位，一个工位包括一台机器，所述缓冲区分为M个，缓冲区与所述工位相对应分配，设相应工位的缓冲区容量配置为K_i≥0，所述库存包括回收件库存、再制造件库存及废弃站库存，设回收件库存为W₀，再制造件库存为W_M+1，废弃站库存为W_M+2，建立回收件在系统中的随机路线，并用矩阵R表示：

式中，r_ij表示从W_i到W_j路径的概率；其中，r_ii表示工位i的返工概率；r_i(M+2)表示工位i的舍弃概率；

(2)将再制造生产线分解为M个独立节点，所述独立节点包括工位和对应缓冲区，在节点前添加一个虚拟节点构成扩展节点，设节点的容量为K_i+1，当回收件到达扩展节点时，检测节点此时包含的回收件数量，若回收件数量小于K_i+1，则回收件进入缓冲区；若回收件数量不小于K_i+1，则回收件无法进入缓冲区转而进入虚拟节点等待，连续检测节点，缓冲区出现空位时，虚拟节点中的回收件就进入缓冲区；

(3)由步骤(2)得缓冲区的状态共有K_i+2种，机器状态有正常和故障两种，但不存在机器故障且缓冲区有0个回收件的状态，则计算节点状态共有2K_i+3个，利用二分法求各节点状态的概率；

(4)根据回收件达到节点的概率，利用牛顿法求解节点到达率和产出率，如果牛顿法在迭代到达一定次数后，仍没有收敛，则选择利用二分法继续求解，在牛顿法中出现的最小区间端点作为初始端点；

(5)根据系统产出率、在制品库存以及舍弃率，求解系统最大化产出率和最小化再制造件库存；

(6)将禁忌搜索与多目标遗传算法-NSGAII相结合，形成多目标算法TS-NSGA II混合算法得到缓冲区的性能指标。

进一步的，步骤(1)中的回收件到达率、机器故障率、维修率及服务率均服从指数分布。

进一步的，在步骤(4)中，设节点i到达率为λ_i，产出率为TR_i，采用牛顿法计算：

式中：为虚拟节点堵塞概率；表示上游回收件到达率，α_i+β_i表示由于故障维修导致的回收件累积，r_iiTR_i表示返工回收件到达率；

根据上式构成关于λ_i的函数f(λ_i)，采用牛顿-二分法求解。

进一步的，在步骤(5)中，设最大化产出率为TR，设最小化在制品库存为WIP，根据步骤(4)得到的节点到达率和产出率计算系统最大化产出率和最小化再制造件库存计算公式为：

最大化产出率：

最小化在制品库存：

步骤(6)中得到缓冲区的性能指标的方法包括以下步骤：

定义n为当前计算的解序号，n＝1,2,3…NA；n_GA为NSGA II算法当前迭代次数，n_GA＝1,2,3…I_GA；I_GA为NSGA II算法的最大迭代次数，即NSGA II算法的终止条件；n_TS为禁忌搜索当前迭代次数，n_TS＝1,2,3…I_TS；I_TS为禁忌搜索的最大迭代次数，即禁忌搜索的终止条件；V＝(V₀,V₁,V₂,…V_M)为插板位置向量，与缓冲区配置向量一一对应，作为解的编码形式，每一个解对应于算法中一个个体，Vn表示第n个解；C₀为初始种群；Π_n为局部最优解；A(V)为领域解集；∏为全局最优解集；F₁为不存在更优个体的个体层级秩，该个体层级秩为1，个体的层级秩为一组个体中，所有更优个体的最低层级秩的下一级；

(61)初始化算法参数，随机产生包含NA个不同个体的初始种群C₀，令n_GA＝1；

(62)令n＝1；

(63)令n_TS＝1，V_n,n_TS＝V_n，初始化局部最优解集∏_n＝{V_n,n_TS}；

(64)生成领域解集A(V_n,n_TS)，评价其每一个解，给出层级秩和拥挤距离；再更新局部最优解集；选择符合禁忌表和特赦准则的A(V_n,n_TS)中最优解赋给V_n,n_TS+1，更新禁忌表；

(65)若n_TS<I_TS，则n_TS＝n_TS+1并转到(4)；否则继续(6)；

(66)若n<NA，则n＝n+1并转到(3)；否则评价∏_n中所有个体，将F₁中解赋给全局最优解集∏；

(67)若n_GA<I_GA，则继续进行(8)；否则跳过步骤(8)直接进行(9)；

(68)n_GA＝n_GA+1，输出每个个体禁忌算法结束时生成的解构成解集Cn_GA，经过交叉操作和变异操作后生成解集Cm。评价所有领域解集的每个解，给出层级秩和拥挤距离，并选择最优的NA个个体赋给Cn_GA。若Cn_GA中不足NA个个体，通过随机生成补齐，并转到(2)；

(69)输出全局最优解集∏。

进一步的，其特征在于，在步骤(6)中，建立禁忌表，所述禁忌表记录局部最优解的属性。

进一步的，其特征在于，在步骤(6)中，禁忌表的禁忌长度设为领域搜索解空间最大规模的10％。

有益效果：相比较现有技术，本发明提供一种再制造系统多目标缓冲区分配方法，该方法在收敛性、多样性以及运行时间方面均效果良好，能够有效解决多目标缓冲区分配问题。

附图说明

图1是一种再制造系统多目标缓冲区分配方法操作流程图；

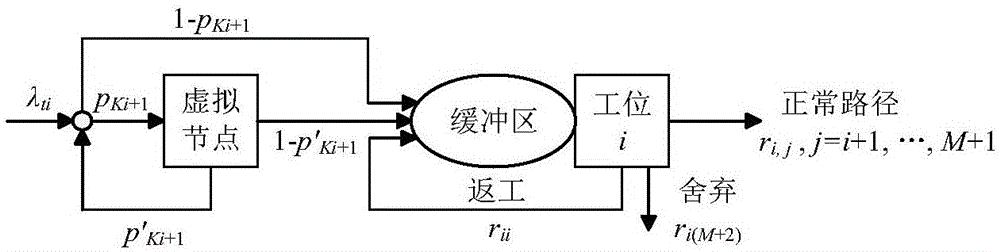
图2是扩展节点示意图；

图3是TS-NSGA II算法流程图；

图4是交叉操作流程图；

图5是变异操作流程图；

图6是5工位、中等规模缓冲区算法效果；

图7是5工位、大规模缓冲区算法效果。

具体实施方式

下面结合附图和具体实施方式，对本发明做进一步说明。

如图1所示，再制造系统多目标缓冲区分配方法操作流程包括以下步骤：

(1)建立再制造系统模型，所述再制造系统模型包括再制造生产线、库存及缓冲区，设再制造生产线包括M个工位，一个工位包括一台机器，所述缓冲区分为M个，缓冲区与所述工位相对应分配，设相应工位的缓冲区容量配置为K_i≥0，所述库存包括回收件库存、再制造件库存及废弃站库存，设回收件库存为W₀，再制造件库存为W_M+1，废弃站库存为W_M+2，假设工件到达服从指数分布e(λ_a)。此外，假定只有当工位处于工作状态时，机器才会发生故障。每台机器的故障率、维修率以及服务率均服从指数分布，参数分别为a_i、b_i和u_i，i＝1,2,…,M。回收件在系统中的随机路线用矩阵R表示。建立回收件在系统中的随机路线，并用矩阵R表示：

式中，r_ij表示从W_i到W_j路径的概率；其中，r_ii表示工位i的返工概率；r_i(M+2)表示工位i的舍弃概率；假设回收件库存中回收件已经过初步检测，不存在直接报废的可能且只考虑同工位返工，因此，r_ij＝0,{(i,j)|i>j,i,j＝1,2,…,M||i＝0,j＝M+1,M+2}。r_ii表示工位i的返工概率；r_i(M+2)表示工位i的舍弃概率。

另外，假设回收件库存中回收件无限提供，再制造件库存、废弃站容量无存储上限。每台机器一次只加工一个回收件。机器加工完工件，若工件对应缓冲区无空间，则工件堵塞在机器上。

(2)将再制造生产线分解为M个独立节点，所述独立节点包括工位和对应缓冲区，如图2所示，在节点前添加一个虚拟节点构成扩展节点，设节点的容量为K_i+1，当回收件到达扩展节点时，检测节点此时包含的回收件数量，若回收件数量小于K_i+1，则回收件进入缓冲区；若回收件数量不小于K_i+1，则回收件无法进入缓冲区转而进入虚拟节点等待，连续检测节点，缓冲区出现空位时，虚拟节点中的回收件就进入缓冲区；

设节点包含的回收件数量为s_i，设节点包含s_i件回收件的概率为则回收件到达扩展节点时进入缓冲区的概率为因此，回收件无法进入缓冲区转而进入虚拟节点的概率为回收件进入虚拟节点后等到缓冲区出现空位后进入缓冲区的概率为反之，被堵塞的概率为

(3)由步骤(2)得缓冲区的状态共有K_i+2种，机器状态有正常和故障两种，但不存在机器故障且缓冲区有0个回收件的状态，则可计算出节点状态共有2K_i+3个，利用二分法求各节点状态的概率；

(4)根据回收件达到节点的概率，利用牛顿法求解节点到达率和产出率，如果牛顿法在迭代到达一定次数后，仍没有收敛，则选择利用二分法继续求解，在牛顿法中出现的最小区间端点作为初始端点；

设节点i到达率为λ_i，产出率为TR_i，为虚拟节点堵塞概率，表示上游回收件到达率，α_i+β_i表示由于故障维修导致的回收件累积，r_iiTR_i表示返工回收件到达率。

式中：

z_i＝(λ_i+2μ_i)²-4λ_iμ_i

由于系统中存在返工，节点i的累积到达率与其产出率有关，根据上式构成关于λ_i的函数f(λ_i)。f(λ_i)是关于λ_i的一元多次方程，选择牛顿–二分法求解。首先利用牛顿法求解，取初值迭代格式为如果牛顿法在迭代到达一定次数后，仍没有收敛，则选择利用二分法继续求解，在牛顿法中出现的最小区间端点作为初始端点。

(5)根据系统产出率、在制品库存以及舍弃率，求解系统最大化产出率和最小化再制造件库存；

设最大化产出率为TR，设最小化在制品库存为WIP，根据步骤(4)得到的节点到达率和产出率计算系统最大化产出率和最小化再制造件库存计算公式为：

最大化产出率：

最小化在制品库存：

(6)将禁忌搜索与多目标遗传算法-NSGA II相结合，形成多目标算法TS-NSGA II混合算法得到缓冲区的性能指标，定义n为当前计算的解序号，n＝1,2,3…NA；n_GA为NSGA II算法当前迭代次数，n_GA＝1,2,3…I_GA；I_GA为NSGA II算法的最大迭代次数，即NSGA II算法的终止条件；n_TS为禁忌搜索当前迭代次数，n_TS＝1,2,3…I_TS；I_TS为禁忌搜索的最大迭代次数，即禁忌搜索的终止条件；V＝(V₀,V₁,V₂,…V_M)为插板位置向量，与缓冲区配置向量一一对应，作为解的编码形式，每一个解对应于算法中一个个体，Vn表示第n个解；C₀为初始种群；Π_n为局部最优解；A(V)为领域解集；∏为全局最优解集；F₁为不存在更优个体的个体层级秩，该个体层级秩为1，个体的层级秩为一组个体中，所有更优个体的最低层级秩的下一级；

具体步骤如图3所示，即：

(61)初始化算法参数，随机产生包含NA个不同个体的初始种群C₀，令n_GA＝1；

(62)令n＝1；

(63)令n_TS＝1，V_n,n_TS＝V_n，初始化局部最优解集∏_n＝{V_n,n_TS}；

(64)生成领域解集A(V_n,n_TS)，评价其每一个解，给出层级秩和拥挤距离；再更新局部最优解集；选择符合禁忌表和特赦准则的A(V_n,n_TS)中最优解赋给V_n,n_TS+1，更新禁忌表；

(65)若n_TS<I_TS，则n_TS＝n_TS+1并转到(4)；否则继续(6)；

(66)若n<NA，则n＝n+1并转到(3)；否则评价∏_n中所有个体，将F₁中解赋给全局最优解集∏；

(67)若n_GA<I_GA，则继续进行(8)；否则跳过步骤(8)直接进行(9)；

(68)n_GA＝n_GA+1，输出每个个体禁忌算法结束时生成的解构成解集Cn_GA，经过交叉操作和变异操作后生成解集Cm。评价所有领域解集的每个解，给出层级秩和拥挤距离，并选择最优的NA个个体赋给Cn_GA。若Cn_GA中不足NA个个体，通过随机生成补齐，并转到(2)；

(69)输出全局最优解集∏。

对算法中一些重要部分解释如下：

(a)编码与初始化种群

编码就是解的遗传基因表示，是算法在实施优化过程的首要问题，也是该算法是否能够成功应用的关键之一。本发明研究缓冲区分配问题，因此缓冲区配置向量为问题的解。为了更好地获得每个解的领域解集以及便于算法操作，本发明选择与缓冲区配置向量一一对应的插板位置向量V＝(V₀,V₁,V₂,…V_M)作为解的编码形式，每一个解对应于算法中一个个体。编码完成后，随机生成具有NA个不同个体组成的初始种群C₀。

(b)评价函数

本发明选用两个评价指标：最大化产出率和最小化在制品库存表征解的性能。已知的评价函数为但是根据该评价函数无法直观地看出解之间的优劣关系，因此选用NSGA II算法的层级秩和拥挤距离来评价一个解的好坏。

(c)领域搜索-禁忌算法

禁忌算法的特点在于其记忆功能，可以用禁忌表记录局部最优解的某些特征，并在下一次搜索中，根据禁忌表中的信息，避免选择或有选择地选择具有这类特征的解，以此保证搜索不同的有效路径，跳出局部最优。

a)领域结构

领域结构的设计直接关系到禁忌算法搜索结果的优劣，其设计原则有：一是领域解集应尽可能多地融入领域知识，保证寻优过程中优解的特征得以传递；二是使得领域规模尽可能小，减少算法单次循环花费的时间，提高算法效率；三是保证领域的连通能力，增强找到局部最优解的可能性。缓冲区分配问题中解为缓冲区配置向量本发明选用插板位置向量V＝(V₀,V₁,V₂,…V_M)进行编码。

根据两者之间的对应关系可知，如果任意一个插板i在满足其位置限制条件的情况下，将其进行前移或者后移仅会改变相邻两个缓冲区i和i+1的容量大小，移动后新的缓冲区配置与现有的缓冲区配置具有很高的相似性，正是领域解集应该具备的特征。假设第n个解V_n＝(V₀,V₁,V₂,…V_M)_n的领域解集为A(V_n)，令V_i(i＝1,2,…,M-1)前移一位或者后移一位构成新解，除去重复出现的解，所有新解构成A(V)。由此可知，领域解集的规模取值为[1,2M-2]，规模恰当。生成A(V_n)后，计算每个解的层级秩和拥挤距离，从而更新局部最优解Π_n。在禁忌搜索条件未满足时，根据禁忌表信息，选择最优解最为下一次禁忌算法迭代的初始解，更新禁忌表。

b)禁忌表与特赦准则

禁忌表的目的是避免迂回搜索并更好地探索领域解的其它区域。禁忌表由若干个禁忌对象构成。将解本身作为禁忌对象尽管比较容易理解，但在实际操作中往往很难实现。在缓冲区分配问题中，解的存储需要占据大量空间，并且需要频繁地检查候选解是否存在与禁忌表中，十分耗时。因此通常选用解的其它属性作为禁忌对象，其中，移动属性的应用最为广泛。本发明同样选择解的移动属性作为禁忌对象，设计为(V_i，D_i)，D_i＝-1表示位置V_i上的插板向前移动一位，D_i＝1表示位置V_i上的插板向后移动一位。

由于解的移动属性只能在一定程度上表征解本身的特征，因此会带来两个方面的问题，一是使得未访问过的解被误禁，二是应该禁的解没有添加进禁忌表。因此引入特赦准则，通过在必要时取消某一移动属性的禁忌状态来避免其被禁。本发明选择的特赦准则为：当某个禁忌对象优于领域最优解集时，对该禁忌对象解禁。

禁忌长度是指不考虑特赦准则的情况下禁忌对象在禁忌表中的任期，记为L。当新禁忌元素加入禁忌表时，最先加入的元素会被这个新元素替换。由于禁忌长度的大小会影响到算法的搜索进程，过小容易造成搜索迂回，过大会降低解的质量。因此需要根据问题特性和算法要求确定。本发明选择禁忌长度大小为领域搜索解空间最大规模的10％。

c)禁忌搜索终止条件

本发明选择常见的最大迭代次数作为禁忌搜索的终止条件，记为I_TS。

(d)交叉操作

如图4所示，从全局最优解中按交叉比例P_c随机选出n_c个体与其随后最优的个体进行交叉，共活动n_c个交叉后的个体，构成解集C_c。交叉操作的流程见图4。

(e)变异操作

如图5所示，从全局最优解中按比例P_m随机选出n_m个体。对每个个体，选取个体中某一插板，插入其它可插位置，获得新的个体。最终产生n_m个变异后的个体，构成解集C_m。变异操作的流程见图5。

(f)NSGA II算法的选择策略和终止条件

第n_GA+1次NSGA II算法迭代初始解从三个解集中抽取最优的NA个解构成，这三个解集分别是n_GA次NSGA II算法迭代禁忌算法得到的最终解集Cn_GA、交叉操作获得的解集C_c、变异操作获得的解集C_m。NSGA II算法的终止条件同样选择最大迭代次数，记为I_GA。

以5工位生产线(M＝5)为例，假设缓冲区总容量具有两个水平：具有中等规模的缓冲区和具有较大规模的缓冲区，分别取N＝{10,15}。此外，假设到达率λ_a为0.5，故障率α_i为0.005，维修率β_i为0.05，i＝1,2,…,M。路径向量R如下

最终选取的算法参数如下表：

每种缓冲区容量下，选用精确算法缓冲区分配的Pareto解集，根据图3所示的算法流程，NSGA II算法和TS-NSGA II算法重复运行4次，得到运行结果。

多目标优化算法的效果需要从最优解集的收敛性、分布性，以及算法的运行时间三个方面进行评价，评价过程如下：

(1)最优解集的收敛性

统计每种缓冲区容量下各算法的平均收敛性指标，见下表。

不同缓冲区容量下算法的收敛性指标

随着缓冲区总容量的增加，解空间规模变大，NSGA II算法以及TS-NSGA II算法找到的最优解数量都随之增加，但两者的递增速率趋势有所不同。可以看出TS-NSGA II算法比NSGAII算法更集中于局部搜索，但搜索广度不如NSGA II算法。然而，两种缓冲区容量条件下TS-NSGA II算法找到的Pareto解的数目比NSGA II算法多，并且其收敛指标均在0.1以下，说明尽管TS-NSGA II算法牺牲了一定程度的搜索范围，但是很好地平衡了TS算法的集中搜索能力和NSGA II算法的分布搜索能力，具有很好的收敛性，比NSGA II算法的寻优效果更好。

(2)最优解集的分布性

为描述两种多目标算法的分布性，绘制每种缓冲区总容量下各算法获得的最优解集的散点图，如图6和图7。图中，虚线是精确算法求得的Pareto最优边界的拟合曲线。

图6中最优解遍布Pareto最优边界，图7中除了异常点外，最优解同样遍布Pareto最优边界，说明NSGA II算法和TS-NSGA II算法获得的最优解集在足够靠近Pareto最优边界的同时，能够保证解的多样性并且不缩小边界范围。结果说明：NSGA II算法和TS-NSGA II算法所求最优解集分布性良好。

(3)算法运行时间

精确算法在计算小规模问题时，运行时间几乎可以忽略不计，具有明显优势。但对于中大规模问题，运行时间长，应当选用进化算法进行求解。尽管TS-NSGA II算法运行时间是NSGA II算法的2-4倍，但是每次运行时间都在30s以内。因此TS-NSGA II算法在运行时间不存在绝对劣势，可以接受。

本领域的普通技术人员将会意识到，这里所述的实施例是为了帮助读者理解本发明的原理，应被理解为发明的保护范围并不局限于这样的特别陈述和实施例。凡是根据上述描述做出各种可能的等同替换或改变，均被认为属于本发明的权利要求的保护范围。