基于金字塔模型的pansharpen融合优化方法与流程

本发明涉及卫星图像处理领域，特别是涉及一种基于金字塔模型的pansharpen融合优化方法。

背景技术：

卫星能够同时获取同一区域两种不同类型的影像：含有高分辨率信息的全色影像以及含有光谱信息的多光谱影像。由于多光谱影像缺少高分辨率信息，全色影像缺少光谱信息，因此上述两种影像自身都会限制遥感影像的使用范围。为了解决上述问题，融合应运而生。时至今日，影像融合的方法很多，但是现有方法很难很好的满足实际生产的需要，纹理畸变和光谱畸变是降低融合结果质量的普遍现象，尤其是随着卫星制造技术的发展，全色影像的光谱范围由传统的可见光谱段延伸到了近红外谱段，部分地物在近红外谱段和可见光谱段表现的光谱差异导致传统的真彩色影像融合方法将引入巨大的光谱畸变，例如将水域的颜色从蓝色变为黑色或者将植被区域的颜色由深绿色变为亮绿色，严重影响到了遥感影像后续的判读和侦查应用。为了满足实际生产的需要，亟需研制一种新的影像融合方法，克服上述的光谱畸变问题。

技术实现要素：

本发明提供一种基于金字塔模型的pansharpen融合优化方法，用于解决现有技术中造成影像融合过程中出现的植被和水域区域的光谱畸变问题，实现可见光影像的高精度真彩色融合处理。

本发明的技术解决方案是：一种基于金字塔模型的pansharpen融合优化方法，包括以下步骤：

步骤1：对全色影像和多光谱影像进行配准处理，并对多光谱影像进行上采样，使得多光谱影像的宽和高与全色影像保持一致；

步骤2：将步骤1中获取的全色影像建立全色影像三层金字塔结构、步骤1中获取的多光谱影像建立多光谱影像三层金字塔结构，然后对全色影像进行下采样，分别获取第一、二、三层金字塔结构对应的遥感影像，对多光谱影像进行下采样，分别获取第一、二、三层金字塔结构对应的遥感影像；

步骤3：分别计算得到全色影像、多光谱影像相同层金字塔结构对应的遥感影像的融合比例系数；

步骤4：对步骤3获得的全色影像、多光谱影像相同层金字塔结构对应的遥感影像的融合比例系数进行最小二乘迭代处理，得到最优的融合比例系数；

步骤5：利用步骤4获取的融合比例系数对步骤1结果中的全色影像和多光谱影像进行融合处理，获取最终的融合图像。

所述的步骤1中所述的对全色影像和多光谱影像进行配准处理的方法，包括如下步骤：

步骤11：对全色影像和多光谱影像分别进行分块处理；

步骤12：对步骤11进行分块处理得到的不同影像块采取SIFT算子提取同名点；

步骤13：构建全色影像和多光谱影像的仿射变换模型，并利用步骤12提取的同名点解算仿射变换模型参数；

步骤14：使用仿射变换模型对多光谱影像进行仿射变换处理，完成影像配准。

所述的步骤1中获取的全色影像建立全色影像三层金字塔结构的方法与步骤1中获取的多光谱影像建立多光谱影像三层金字塔结构的方法相同，对全色影像进行下采样，分别获取第一、二、三层金字塔结构对应的遥感影像与对多光谱影像进行下采样，分别获取第一、二、三层金字塔结构对应的遥感影像的方法相同，其中，将步骤1中获取的全色影像建立全色影像三层金字塔结构，然后对全色影像进行下采样，分别获取第一、二、三层金字塔结构对应的遥感影像的方法包括如下步骤：

步骤21：构建128像素*128像素,1024像素*1024像素,4096像素*4096像素大小的全色影像三层金字塔；

步骤22：分别计算全色影像三层金字塔中不同层的宽、高与步骤1得到的全色影像宽高的比例，并对应分别作为全色影像三层金字塔不同层的下采样比例系数；

步骤23：使用步骤22得到的下采样比例系数分别对步骤1得到的全色影像进行下采样处理，获取全色影像第一、二、三层金字塔结构对应的遥感影像。

所述的分别计算得到全色影像、多光谱影像相同层金字塔结构对应的遥感影像的融合比例系数的方法包括如下步骤：

步骤31：构建全色影像第j层金字塔结构对应的遥感影像、多光谱影像的光谱能量关系函数，j等于一或二或三；其中，光谱能量关系函数为P表示全色影像的某一个像素的灰度值，α_i表示谱段i对应的能量配比系数，M表示多光谱影像上对应的同名像素的灰度值，i表示多光谱的谱段个数；

步骤32：引入不等条件约束，保证光谱能量关系函数中待求解的参数α_i均大于0，进而得到不等条件约束方程；所述的不等条件约束方程包括不等条件约束、光谱能量关系函数；

步骤32：将全色影像、多光谱影像第j层金字塔结构对应的遥感影像所有像素的灰度值代入到方程中，进行迭代求解，得到第j层对应的光谱能量关系函数中待求解的参数α_i的解，遍历所有的j，得到所有层对应的光谱能量关系函数中待求解的参数α_i的解，并作为融合比例系数。

所述的对步骤3获得的全色影像、多光谱影像相同层金字塔结构对应的遥感影像的融合比例系数进行最小二乘迭代处理，得到最优的融合比例系数的方法为：将三组不同的融合比例系数代入到线性最小二乘模型中，将线性最小二乘模型的解作为最优的融合比例系数。

本发明与现有技术相比具有如下优点：

(1)本发明利用多光谱的谱段信息，构建全色和多光谱之间的能量配比关系，能够有效抑制影像中出现的光谱畸变现象；

(2)本发明通过引入不等条件约束方程，限定能量配比系数的大小，避免了融合过程中出现“黑洞”现象，导致纹理细节丢失；

(3)本发明通过引入金字塔模型，避免了大数据的迭代计算，节省了计算资源并提高了计算效率；

(4)本发明可以达到融合影像的细节保持度优于95％，光谱保真度优于98％，基本克服了光谱畸变的影响。

附图说明

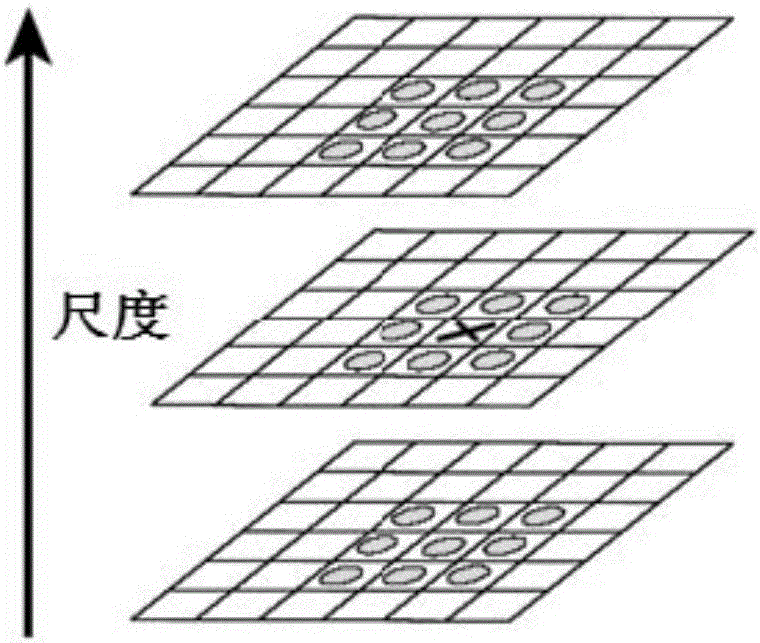
图1为SIFT算子DOG尺度空间局部极值检测示意图

图2为本发明的基于金字塔模型的pansharpen融合优化方法算法流程图。

具体实施方式

本发明提出了一种基于金字塔模型的pansharpen融合优化方法，该方法通过求取全色影像和多光谱影像之间的能量配比系数，有效的克服了传统影像融合方法中造成的现有遥感影像融合时出现的水域和植被区域较大的光谱畸变现象，同时该方法通过构建不等条件约束方程，约束能量配比系数的大小，从而确保融合结果中不会出现无效数据，从整体上提高了影像融合中细节保留度和光谱保真度，最后该方法引入金字塔模型，简化了计算复杂度，提高了计算效率。

如图2所示为基于金字塔模型的pansharpen融合优化方法算法流程，本发明的具体步骤如下：

步骤1：对全色影像和多光谱影像进行配准处理，并对多光谱影像进行上采样，使得多光谱影像的宽和高与全色影像保持一致。

i.利用SIFT算子提取同名点

SIFT特征算子高精度同名点提取方法主要包含两个部分：特征点提取，特征点匹配以及粗差剔除。

SIFT特征算子是基于多尺度空间理论来进行特征点提取的，为了有效的在尺度空间检测到稳定的关键点，SIFT算子提出了高斯差分尺度空间(DOG scale-space)。利用不同尺度的高斯差分核与图像卷积生成。

D(x,y,σ)＝(G(x,y,kσ)-G(x,y,σ))*I(x,y)＝L(x,y,kσ)-L(x,y,σ)

DOG算子计算简单，是尺度归一化的LOG算子的近似。为了寻找尺度空间的极值点，每一个采样点要和它所有的相邻点比较，看其是否比它的图像域和尺度域的相邻点大或者小。如图1所示，中间的检测点和它同尺度的8个相邻点和上下相邻尺度对应的9×2个点共26个点比较，以确保在尺度空间和二维图像空间都检测到极值点。

通过拟和三维二次函数以精确确定关键点的位置和尺度(达到亚像素精度)，同时去除低对比度的关键点和不稳定的边缘响应点(因为DOG算子会产生较强的边缘响应)，以增强匹配稳定性、提高抗噪声能力。

在获取了特征点后需要对不同影像的特征点进行匹配处理，本发明采用关键点特征向量的欧式距离来作为两幅图像中关键点的相似性判定度量。取全色图像中的某个关键点，并找出其与多光谱图像中欧式距离最近的前两个关键点，在这两个关键点中，如果最近的距离除以次近的距离少于某个比例阈值，则接受这一对匹配点，否则不接受这对匹配点，如此反复计算获取全部同名点的像素位置信息。

ii.构建仿射变换模型

仿射变换模型的公式如下所示：

式中,x、y表示多光谱影像上同名点的像素坐标，x'、y'表示全色影像上同名点的像素坐标，m₀₀、m₀₁、m₀₂、m₁₀、m₁₁、m₁₂表示仿射变换系数。

由于仿射变换系数有6个，因此至少要有4对同名点的像素位置关系才能进行系数解算处理。

iii.多光谱影像上采样处理

在获取了仿射变换系数后，可以对多光谱影像进行仿射变换处理。先构建几何关系格网，建立仿射变换结果与原始图像之间的几何关系，通过位置之间的关系将原始图像的灰度值填充到放射变换结果中，最后对多光谱影像进行上采样处理，上采样方法为将1个像素变为2*2的像素矩阵，且用该像素值填充像素矩阵。

步骤2：对步骤1中获取的配准影像分别建立三层金字塔，并通过下采样获取不同金字塔对应的灰度影像：

i.计算不同层宽高与配准后影像宽高的比例关系作为下采样比例

由于三层金字塔的大小分别为128*128，1024*1024，4096*4096，因此需要首先计算下采样的比例系数，才能从原始影像中获取不同层的缩略图，其中金字塔的大小是在考虑现有遥感影像的实际幅宽大小以及计算资源的大小基础上决定的，比例系数的计算公式如下：

x＝N/n,y＝M/m

式中，M和N表示原始影像的大小，m和n表示金字塔的大小，x和y表示下采样的比例系数。

ii.分别对配准后的全色影像和多光谱影像进行下采样处理：

利用上一步中获取的下采样比例系数，下采样方法为在X方向，x个像素合并为一个像素，Y方向上，y个像素合并为一个像素。

步骤3：构建不等条件约束模型，分别求取不同层金子塔模型下的融合比例系数。

i.构建全色影像和多光谱影像的能量配比函数：

考虑到全色影像的光谱范围涵盖了多光谱的可将光和近红外4个谱段的光谱范围，因此可以认为，在同样的拍摄模式下，即卫星载荷“五谱合一”器件的光学结构设计下，获取的全色影像和多光谱影像之间应该满足如下的线性函数关系：

式中，P表示全色影像的某一个像素的DN值，α表示能量配比系数，M表示多光谱影像上对应的同名像素的DN值，i表示多光谱的谱段个数。

ii.引入不等条件约束方程，保证配比函数中待求解参数均大于0：

为了求解能量配比函数中的参数，需要构建如下方程

式中，γ表示不等条件函数的比例系数。对其求偏微分，获取如下方程：

对上式进行离散化处理，获取如下方程：

式中，τ表示迭代间隔大小，N的最大值取值为n。通过上述迭代方程，即可求解能量配比函数中的参数值。

iii.用同样方式对不同层采取同样的迭代方式获取不同层的融合比例系数

步骤4：对获得的不同层比例系数进行最小二乘迭代处理，获取最优的融合比例系数。

将三个不同的融合系数代入到现行最小二乘模型中，获取全色影像和多光谱影像最优的能量配比关系参数，做为最终的融合系数。

本发明说明书中未作详细描述的内容属本领域技术人员的公知技术。