基于Spark内存计算大数据平台的OPTICS点排序聚类方法与流程

本发明涉及计算机数据挖掘、计算机信息处理技术领域。

背景技术：

随着计算机信息领域的飞速发展，大量的数据从生活的各个方面被收集起来，互联网上各种各样信息的规模也在成几何倍数的增大，从海量的数据中迅速分析从而提取隐藏在数据中的信息变得越来越重要。

聚类分析是数据分析的一个主要方法，聚类(clustering)是将数据对象进行分类的过程，使同一簇中的对象之间具有很高的相似度，而不同簇中的对象高度相异。与分类过程不同的是，聚类不依赖预先定义的类和类标号，同时聚类过程中的分类标准和类型数量均是未知的。近来聚类分析方法得到了相当多的关注。传统的聚类分析算法存在三个问题：第一，需要输入参数，但输入参数难以获取；第二，对输入参数特别敏感，参数设置的细微不同可能导致聚类的差别很大；第三，高维的数据集一般都具有非常倾斜的分布，全局密度参数不能刻画内置的聚类结构。

基于密度的聚类方法OPTICS(Ordering Point To Identify the Cluster Structure)是通过扩展传统的DBSCAN(Density-Based Spatial Clustering of Applications with Noise)算法，对数据集中数据对象通过计算基于密度的簇排序，从簇排序序列中提取有用的聚类信息的数据分析方法。OPTICS算法相对于传统的聚类算法，对输入参数不敏感。

随着数据量的增大和数据维度的增加，采用传统的串行方法难以应对百万条以上的数据集，通常会出现时间过长，内存溢出和宕机等问题，不能满足现实中工程的需要。Spark是一个基于内存的分布式计算系统，是由UC Berkeley AMPLab实验室开发的开源数据分析集群计算框架。拥有MapReduce的所有优点，与MapReduce不同的是，Spark将计算的中间结果数据持久地存储在内存中，通过减少磁盘I/O，使后续的数据运算效率更高。Spark的这种架构设计尤其适合于机器学习、交互式数据分析等应用。这些应用都需要重复地利用计算的中间数据。在Spark(基于内存计算框架)和Hadoop MapReduce(并行计算框架)的性能基准测试对比中，运行基于内存的logistic regression，在迭代次数相同的情况下，Spark的性能超出Hadoop MapReduce 100倍以上。两者之间在计算过程中也存在一些不同之处，比如MapReduce输出的中间结果需要读写HDFS，而Spark框架会把中间结果保存在内存中。这些不同之处使Spark在某些工作负载方面表现得更加优越，换句话说，Spark启用了内存分布数据集，除了能够提供交互式查询外，它还可以优化迭代工作负载，因此Spark能更好地适用于数据挖掘与机器学习等需要迭代的MapReduce的算法。而弹性分布式数据集(RDD，Resilient Distributed Datasets)是Spark框架的核心数据结构，它具备像MapReduce等数据流模型的容错特性，并且允许开发人员在大型集群上执行基于内存的计算。Spark将数据集运行的中间结果保存在内存中能够极大地提高性能，资源开销也极低，非常适合多次迭代的机器学习算法。

文章ZAHARIA M,CHOWDHURY M,FRANKLIN M J,et al.Spark:cluster computing with working sets[C]//Book of Extremes.2010:1765-1773.采用基于Spark大数据平台并行聚类方法，能够快速的处理大规模的数据集。Spark的核心是RDD(resilient distributed dataset)，是一个只读的，可分区的分布式数据集，这个数据集的全部或部分可以缓存在内存中，在多次计算间重用。传统的MapReduce虽然具有自动容错、平衡负载和可拓展性的优点，但是其最大缺点是采用非循环式的数据流模型，使得在迭代计算时要进行大量的磁盘IO操作。RDD正是解决这一缺点的方法。

技术实现要素：

本发明所要解决的技术问题是，针对现有技术在处理大批量数据时进行聚类容易内存溢出、时间过长和无法运行宕机等缺点，本发明提出一种基于Spark(基于内存计算平台)大数据平台的通过点排序识别聚类结构OPTICS(Ordering Points To Identify The Clustering Structure)算法，能够处理大批量的数据集，并可以在极短的时间内得到簇排序。能够有效的解决上述问题，并可以在不同层次观察导出内在的聚类结构，满足用户的期望输出。

本发明解决上述问题的技术方案是，提出一种基于内存计算Spark大数据平台的OPTICS算法，具体包括：读取大规模数据集，创建分布式数据集RDD，完成初始化操作；对数据结构进行并行划分，得到最优数据集分区；根据最优数据集分区生成的RDD，并行计算邻居样本数量和核心距离，对每个分区并行执行OPTICS(通过点排序识别聚类结构)算法可以得到每个分区的簇排序并持久化存储；通过簇排序给每个分区赋予簇号，合并分区，使每个样本得到全局的簇号。

本发明利用Spark分布式并行技术，找到数据结构的最优划分结构，并行计算得到每个分区的簇排序，通过OPTICS算法的簇排序，用户可以从不同层次结构观察数据集的内在聚类结构。本发明具体包括以下步骤：从分布式文件系统HDFS(Hadoop Distributed File System，Hadoop)上读入数据集，并创建一个Spark的上下文SparkContext(程序运行初始环境)对象，利用对象的抽象数据结构函数parallelize(DataSet)或textFile(DataSet URL)创建分布式数据集RDD，创建完成的分布式数据集可以被并行操作。把RDD中每个样本通过map()(每行数据执行同一操作的函数)函数转换为对应的自定义类Point(用来存储每个样本的各种信息)，Point类中存储有每个样本的值及其相关信息。可以输入聚类初始的半径ε和半径内最小的邻居数MinPts。

对RDD进行划分得到数据集的最优结构，具体可采用如下方法：

(1)通过RDD的行动函数(reduce()或者fold()(一种通过折叠RDD来计算整个RDD信息的函数))计算数据集的所有维度,得到维度数N(一般维度差异最大的有5个维度)，广播整个数据集。

(2)把RDD分成N个分区，每个分区能够获取到前面的广播变量，每个分区分别根据相关维度，各自生成树形结构。树的每个节点都是一个盒子(box类)，盒子有前边界和后边界及存储包括的样本数组。生成树形结构时，按照维度进行数据集的划分。首先按照维度将数据集等距离进行平分，形成两个盒子，这两个盒子再进行等距离平分，直到盒子的样本数据个数小于设定值或者盒子的前边界值减去后边界值小于2×ε。标记每个样本属于的盒子，或是否属于每个盒子的前后边界。标记每个样本与所属盒子的前后边界的关系。例如某个样本点到所属盒子的前边界线的距离小于ε，则为此盒子的前边界点，若到所属盒子的后边界线的距离小于ε，则为此盒子的后边界点。

(3)遍历所有分区的划分树，得到盒子数组。调用Spark平台所提供的累加变量，汇集所有分区盒子数组的情况，寻找到盒子数组划分均匀并且盒子数组长度最多的分区，得到最优分割分区。具体可采用如下方法：每个分区都获取自己分区的盒子数组的总长度L，每个分区的对应的盒子数组中样本个数最多的样本数M，盒子数组的平均样本数N，根据公式P＝N/M计算判断倾斜的标准。每个分区的L和P标准化，取L+P值最大的分区为最优分割分区，保存最优分割分区，去掉其余分区。保存的最优分割分区其内部的盒子数组就是最优划分结构的盒子数组。

进一步地，可根据最优分割分区的最优划分结构的盒子数组得到新的RDD，并计算样本邻居和样本点的核心距离，具体可包括如下方法：

(1)首先广播整个盒子数组(即把盒子数组分发到每台机器并存储一个副本,可理解为每个分区都会得到一个盒子数组的副本，减少大幅度任务计算的时间)，另外再单独把盒子数组生成为RDD结构，RDD每个分区分别获得序号相对应的盒子。例如RDD的0号分区获得盒子数组的0号盒子，依次类推。因为盒子数组和RDD的盒子本身储存的样本点都是一样，广播处理的话可加快计算的速度。

(2)每个RDD分区中的盒子分别与广播的盒子数组中其序号对应的盒子及其序号前后盒子进行计算样本邻居。例如0号分区与盒子数组的0号和1号盒子进行计算，1号分区与1号，0号和2号盒子进行计算，依次类推。因为每个盒子存储的都是大量的样本点，分区中的盒子与其序号对应的盒子进行计算样本点与样本点之间的距离，可得到一个样本点周围有哪些样本点是其邻居样本点。而分区中盒子与其序号对应前后的盒子计算点与点之间欧几里得距离是为了计算分区盒子中边界点和前后盒子中边界点是否是邻居关系。是否是邻居样本点的判断标准取决于用户设定的阈值。

(3)根据邻居样本点及与其目标样本点的欧几里得距离，根据如下公式(1)计算得到每个样本的核心距离。

core-dist_ε，MinPts(p)表示样本点P的核心距离，其中ε表示样本点P的邻域半径，MinPts表示使得样本点P成为核心样本点的最小邻居样本点个数，core-dist表示核心距离。

if|N_ε(p)|＜MinPts表示当样本点P周围的邻居样本点个数小于设定阈值个数MinPts时，其中，|N_ε(p)|表示样本点P周围的的邻居样本点个数。UNDEFINED表示此时P的核心距离无定义。

MinPts-th smallest distance to N_ε(p)表示使得样本点P周围至少有MinPts个邻居样本点的最小邻域半径，其中MinPts-th smallest distance表示满足MinPts邻居样本点个数最小半径距离。

根据公式(2)计算每个样本的可达距离：

其中，reachability-dist_ε,MinPts(o,p)表示样本点O到样本点P的可达距离，reachability-dist表示可达距离，Max(core-dist_ε，MinPts(p),dist(p,o))表示取样本点P的核心距离和样本点P和样本O的欧式距离中最大的一个，dist表示distance的欧几里得距离。

按照最优结构划分并计算距离得到每个分区中每个样本点(Point类)的邻居样本点，并把邻居样本点的序号存储到样本点(Point类)后，每个分区进行经典OPTICS(通过点排序识别聚类结构)算法，对所有样本的可达距离进行排序，每个分区得到簇排序，调用saveAsTextFile(“outpath”)(把RDD存储到hadoop分布式文件系统的函数)函数将簇排序持久化存储。每个分区的簇排序只能进行数据结构层面上观测作用，而为了得到每个样本点的最终簇号，需要输出聚类结果。所以根据每个分区的簇排序，可以依照用户的需求在不同层次结构上得到簇号，然后合并分区，输出聚类的结果。具体包括：

(1)根据用户输入的判断距离阈值B，从每个分区的簇排序中按顺序提取样本，首先先设定一个初始类别，如果该样本的可达距离不大于B则属于当前正在判定的类别。如果样本的可达距离大于B且核心距离大于B，则为噪声。如果样本的可达距离大于B且核心距离小于B，则属于下一个新的类别，则另起一个新的类别。

(2)生成全局合并簇号的Map(键值对应的数据存储结构)，保留每个分区的边界样本形成盒子边界数组，广播该数组。按每个分区的前边界点和数组序号对应的前一个盒子的后边界点进行循环，如果存在一对样本的距离小于给定B，则加入Map中。

(3)每个分区根据该Map合并簇号，并输出最终的聚类结果，如不符合期望公式，期望公式:已分配簇号的样本数/总样本数>＝0.8(阈值0.8可以根据用户的实际情况进行调整)，则可以返回步骤(1)，直到符合期望公式为止。

本发明提出了基于Spark平台的OPTICS算法，能够处理大批量的数据集，并可以在极短的时间内得到簇排序。用户可根据簇排序和自身的实际需求，得到最后的聚类结果。该方法能有效提高大规模数据的计算效率，更加符合数据量快速增长的实际应用场景，能够明显提高数据挖掘的效率，具有较好的实际应用价值且成本较低。

附图说明

图1基于Spark大数据平台的OPTICS聚类算法流程框图；

图2基于Spark大数据平台的数据分块部分的流程框图；

图3基于Spark大数据平台计算邻居数流程框图；

图4基于Spark大数据平台OPTICS聚类算法的流程框图；

图5基于Spark大数据平台合并分区部分流程框图；

图6按照分区维度对数据集进行划分过程示意图；

图7广播的盒子数组示意图例。

具体实施方式

RDD(弹性分布式数据集)是一种有容错机制的特殊集合，可以分布在集群的节点上，以函数式编辑操作集合的方式，进行各种并行操作，RDD为一个具有容错机制的特殊集合它提供了一种只读、只能有已存在的RDD变换而来的共享内存，然后将所有数据都加载到内存中，方便进行多次重用。RDD是分布式的，可以分布在多台机器上，进行计算，并且RDD是弹性的，计算过程中内存不够时它会和磁盘进行数据交换。而Spark技术因其是基于内存的计算，基于Spark的聚类方法大多采用对数据集先进行划分，在每个小块数据集上样本点先聚合成小类，再不断的合并小块数据集中的小类别，最后聚合得到最终的大类别。能够很好地解决Hadoop平台存在内存溢出、时间过长和无法运行宕机等缺点。

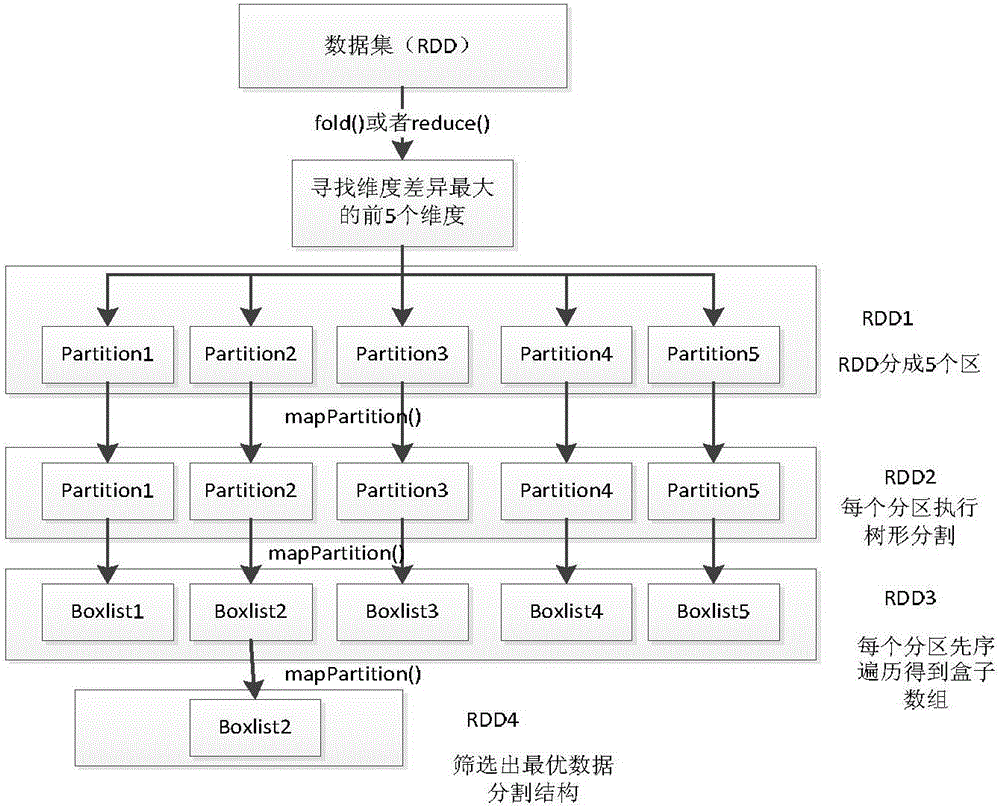
以下结合附图和具体实例对本发明的实施作进一步具体描述。图1为本发明基于Spark大数据平台的OPTICS聚类算法流程框图，创建分布式数据集RDD，寻找最优结构，完成对数据分块；计算每个点的邻居数，得到其核心距离；对每个分区并行执行OPTICS，获得簇排序；在分区内标记族号获取全局合并族号map，合并分区并输出聚类结果。具体包括如下步骤：

(1)数据分块阶段

如图2所示为基于Spark大数据平台的数据分块部分流程图。输入需要聚类的数据集，将其转换成Spark平台的分布式数据集RDD，并且完成初始化操作。首先根据输入的数据集创建一个SparkContext对象(SparkContext是程序的入口，负责连接Spark集群，创建RDD(分布式数据集)，累积量和广播量等)。然后调用对象的parallelize(DataSet)或textFile(DataSetURL)(数据集转换为RDD函数)创建分布式数据集，一旦创建完成，这个分布式数据集就可以被并行操作。即RDD＝sc.textFile(DataSetURL)；把当前的RDD中每个样本通过map()函数转换为对应的Point(自定义类包括样本点及其详细信息)类，Point类中存储每个样本的值及其相关的信息。

根据预先输入的聚类初始半径ε和半径内最小的邻居数MinPts，RDD开始寻找数据集的最优划分结构，把数据集的样本点合理均匀的划分到各个盒子中，并把数据集转换成一个包含所有样本点的盒子数组。通过RDD的行动函数(reduce()或者fold())计算得到数据集维度差异最大的所有N个维度，广播整个数据集到每一个分区中，每个区会得到整个数据集的一个副本，广播操作可大幅度减少计算的时间。将RDD分成N个分区，每个分区均能够获取到前面的广播变量，每个分区分别根据相关维度各自生成一种树形结构，树形结构的每个节点都是一个盒子(box类)，盒子有前边界和后边界及存储的样本数组。生成树时，按照分区所得到的维度进行数据集的划分。具体可采用如下方法：先平分广播时每个分区所得到的整个数据集副本形成两个盒子，将两个盒子的样本数据再进行平分，直到每个盒子的样本数据个数小于设定值或者盒子的前边界值减去后边界值小于2倍ε。标记每个样本点与所属盒子的前后边界的关系。例如某个样本点到所属盒子的前边界线的距离小于ε，则此盒子的前边界点，若到所属盒子的后边界线的距离小于ε，则此盒子的后边界点。

按每个分区遍历各自生成划分树。通过Spark的累加变量汇集所有分区的盒子数组情况，寻找盒子数组划分较均匀并且盒子数组长度较多的分区。具体可采用如下方法：根据盒子数组的长度L，所有分区的盒子数组中样本个数最多的盒子中的样本数M，求得数组平均盒子的样本数为N＝数据集的总样本数G/盒子数组的长度L，则判断倾斜标准值P＝N/M。标准化每个分区的L和P，L+P值最大的分区就是最优分割分区，保存最优分割分区，去掉其余分区。

(2)并行计算邻居阶段

图3所示为计算邻居数部分流程框图。对最优分割分区将盒子分配到对应的分区，盒子数组的0号盒子分到0号分区，1号盒子分到1号分区，依次类推，每个分区分别获得序号相对应的盒子，可得到每个分区都存储一个盒子的RDD，另外广播整个盒子数组到每一个分区中，每个分区都得到了一个完整的盒子数组的副本。每个分区的每个盒子都调取mapPartition()函数，mapPartition函数是每个分区的所有样本点一起调用一次，每个分区的盒子分别与广播的盒子数组中其序号对应的盒子的样本点及其序号前后盒子样本点进行计算欧几里得距离，然后每个盒子里的每个样本点都能得到邻居样本点。例如，1号分区的样本与盒子数组的1号盒子的样本计算欧几里得距离，1号分区的前边界样本与盒子数组的0号盒子的后边界样本点计算欧几里得距离，1号分区的后边界样本与盒子数组的2号盒子的前边界样本计算欧几里得距离，判断距离是否小于阈值，可得到是否是其邻居，依次类推。分区中盒子与其序号对应前后的盒子计算点与点之间距离是为了计算分区盒子中边界点和前后盒子中边界点是否是邻居关系，而是否是邻居样本点的判断标准取决于用户设定的阈值。每个分区根据邻居数及对应的距离，得到每个样本对应的核心距离。最后每个分区的每个样本点都会得到一系列的邻居样本点编号，保存在自身的Point类中。

可采用如下公式(1)计算每个样本的核心距离，

core-dist_ε,MinPts(p)表示对于样本点P的核心距离，其中ε表示样本点P的邻域半径，MinPts表示使得样本点P成为核心样本点的最小邻居样本点个数，core-dist表示核心距离。

if|N_ε(p)|＜MinPts表示当样本点P周围的邻居样本点个数小于设定阈值个数MinPts时，其中|N_ε(p)|表示样本点P周围的的邻居样本点个数。

UNDEFINED表示此时P的核心距离无定义。

MinPts-th smallest distance to N_ε(p)表示使得样本点P周围至少有MinPts个邻居样本点的最小邻域半径，其中MinPts-th smallest distance表示满足MinPts邻居样本点个数最小半径距离。

根据公式(2)计算每个样本的可达距离：

reachability-dist_ε,MinPts(o,p)表示样本点O到样本点P的可达距离，reachability-dist表示可达距离

Max(core-dist_ε,MinPts(p),dist(p,o))表示取样本点P的核心距离和样本点P和样本O的欧几里得距离中最大的一个，其中dist表示distance的欧几里得距离。

(3)OPTICS聚类阶段

如图4所示为OPTICS聚类算法的流程。每个分区的样本并行的执行OPTICS(通过点排序识别聚类结构)聚类算法，每个分区各自得到各个分区所有样本点的可达距离形成序列，称为分区可达序列。具体采用如下方法：

Step1:初始化：结果队列初始为空,全局邻居数组初始为空；

Step2:选择一个未处理样本点放入全局邻居数组:

Step3:如果全局邻居数组为空,返回Step 2,否则选择第一个对象p进行扩张:

Step3.1:如果p不是核心点,转Step 4；否则,对p的ε邻域内任一未处理的邻居q计算欧式距离:

Step 3.1.1:如果q已在全局邻居数组中且从p到q的可达距离小于此时q的可达距离,则更新q的可达距离,并根据q的新的可达距离，调整q到全局邻居数组中相应位置，以保证队列的有序性；

Step3.1.2:如果q不在全局邻居数组中,则根据p到q的可达距离将其插入有序队列；

Step 4:从全局邻居数组中删除p，并将p写入结果队列中,返回Step3。

最后每个分区的结果序列就是我们所求的簇排序，并调用saveAsTextFile(“outpath”)(将RDD序列化存储到分布式文件系统的函数)函数将聚类后的RDD做持久化存储，把每个分区的簇排序保存到HDFS上。

(4)合并分区及簇号阶段

根据每个分区的簇排序，可以依照用户的需求在不同层次结构上得到簇号，然后进行合并分区，输出聚类的结果。

根据用户输入的结果距离值B，从每个分区的簇排序中按顺序提取样本，先给出一个类别，如果该样本的可达距离不大于B则属于当前正在处理的类别，则把样本点所属的Point类的类别属性标记当前类别。如果可达距离大于B并且核心距离大于B，则把样本点所属的Point类的类别属性标记噪声。如果当可达距离大于B并且核心距离小于B，则把样本点所属的Point类的类别属性标记下一个新的类别。

将得到簇号的RDD调用map()函数，留下每个分区的前后边界点为分布式数据集RDD1，RDD1调用collect()(把RDD转换为数组的函数)函数把RDD1转换为数组并广播。然后RDD1通过mapPartition()(一个分区调用一次这个函数)与广播变量进行全局合并获得map(键值对形式数据储存结构)

如图5所示合并分区部分流程框图，根据RDD1的1号分区的前边界样本和广播变量的0号元素的后边界点计算map，map的方向由后指向前，向前合并簇号，把合并的簇号加入到map中。

每个分区所有样本点都根据Map(键值对形式数据储存结构)合并簇号，并输出最终的所有样本点的簇号，相同簇号的放在一起输出到文件中，最后将文件进行持久化的保存。

以下举例对本发明的实施作进一步说明。本实施例在以本发明技术方案为前提下进行实施，给出了详细的实施方式和具体的操作过程，但本发明的保护范围不限于下述的实施例。

假如有一数据集有10个样本，维度为2，数据集具体为{(1,3),(2,3),(1,2),(2,2),(3,3),(4,4),(5,4),(4,5),(5,5),(6,5)}，初始的聚类半径ε为1和半径内最小的邻居数MinPts为3。

首先读取这个数据集，并转换为分布式数据集RDD，再通过map()函数把数据集的每一个样本点转换为Point类，Point类中包括样本点和样本的相关信息(如样本的编号，是否为边界点，邻居数组，核心距离，可达距离，属于哪个盒子和是否被访问等)。

进入数据分块阶段，寻找维度差异最大的5个维度，通过reduce()或者fold函数进行分布式查找，数据集只有2维，则取数据集的所有维度进行查找最优的结构划分。先用collect函数把RDD转换数组并广播出去。将RDD分为两个parttion(分区)每个partition(分区)按照1个维度进行树形结构划分。树的每个节点都是一个盒子(box类)，盒子有前边界和后边界及存储包括的样本数组。

按照分区的维度对数据集进行划分，生成树状结构。首先将数据集的所有数据按照第一维度进行平分形成两个盒子，两个盒子的边界分别为(1,3.5)和(3.5,6)，所以此时{(1,3),(2,3),(1,2),(2,2),(3,3)}属于第一个盒子，其余的样本点属于第二个盒子，两个盒子的数据再按照第一维度进行平分，直到盒子中的样本数据个数小于设定值或者盒子的前边界值减去后边界值小于2倍ε，结束数据划分。标记每个数据样本属于这个盒子是否属于每个盒子的前后边界。例如(1,1)样本点到所属盒子的前边界线的值1的距离小于ε值1，则为此盒子的前边界点，而(2.2)样本点到所属盒子的后边界线值2.25的距离小于ε值1，则为此盒子的后边界点。

划分过程如图6所示，图6为按照分区维度对数据集进行划分过程示意图。(a)图按照第一维度生成划分树，第一次计算得到划分边界为1+6/2＝3.5,所以根节点的左孩子的盒子的边界为(1,3.5)，右孩子的边界为(3.5，6)，所有样本点按照边界分别归进两个盒子中。此后两个盒子再进行划分，当满足盒子的前后边界值之差小于两倍ε或者盒子中样本数量小于MinPts，停止分裂。(b)图是按照第二维度进行划分，划分出来的两个盒子边界范围(3，4)，(4,5)，第二次划分因盒子的前后边界值之差小于两倍ε，所以停止分裂。

此时两个分区都得到一个树形结构，通过树的先序遍历可各自得到一个盒子数组。因为在划分时是按等距离进行划分的，所以寻找到盒子数组划分样本点数量较均匀并且盒子数组长度较多的分区，并保留此分区，避免计算时数据倾斜。

具体可采用如下方法判断为，首先盒子数组的长度为L，每个分区的盒子数组中样本个数最多的盒子为a，盒子a中所有样本数有M个，求得数组平均盒子的样本数为N个和判断是否平均的标准值P＝N/M。再把每个分区的L和P标准化，L+P的值最大的分区就是最优的分割分区，保存这一分区，其余分区均去掉。通过累加变量可得到各个分区的盒子数组的具体信息，此时0号分区的盒子数组长度为4,1号分区为2，0号分区的样本数量最多盒子样本数为4,1号分区为5,0号分区的平均盒子样本数为:10/4＝2.5，1号分区为:10/2＝5。标准化后两个分区L+P值分别为1.625和1.5，所以0号分区的盒子数组是最优的划分结构，按照0号分区进行划分。

计算邻居阶段，此前得到4个盒子，每个盒子内部的样本点需标明是当前盒子的前边界点或后边界点或既是前边界点又是后边界点或内部点。先把这个盒子数组广播出去，减少计算时的计算开销。然后新建一个RDD把这个盒子数组放进去，0号分区放0号盒子，1号分区放1号盒子，依次类推。如图7所示为广播的盒子数组示意图。

每个分区调取mapPartition()函数分别与前面广播的盒子数组中其对应的盒子及其前后盒子进行计算距离并得到所有样本邻居的编号。1号分区的(3,3)样本与盒子数组的1号盒子的(3,3)样本进行计算欧几里得距离，1号分区的前边界样本(3,3)与盒子数组的0号盒子的后边界样本(2,3)和(2,2)进行计算欧几里得距离，1号分区的后边界样本(3,3)与盒子数组的2号盒子的前边界样本(4,4)和(4,5)进行计算距离并得到该样本点所有邻居的编号，保存在样本点的Point类中，依次类推。每个分区的每个样本点根据邻居数及对应的距离，得到每个样本对应的核心距离。

然后每个分区并行执行OPTICS算法，得到簇排序。根据用户键入的判断结果值1，可给每个分区的点标记上分区簇号，簇号结构为(分区号，分区内的簇号)，噪声则为(-1,-1)。

因1号分区的(3,3)样本的邻居为(2,3)，(3,3)小于MinPts,则为噪声点。而2号分区的样本(4,4)有(4，4)，(4，5)，(5,4)为邻居，则不是噪声点有簇号。

最后进入求合并map的阶段，如图5，先把不是边界点的样本去掉，本例中无内部点，所以全部都留下来。再用collect函数得到数组并广播出去。Map的格式为(分区号，分区簇号，噪声样本的编号)。如RDD的1号分区的前边界样本(3,3)和广播变量的0号元素的后边界样本(2,2)计算map，因为(3,3)是噪声样本，为了避免噪声样本过多，所以需保留噪声样本的编号，而不是噪声样本则不需要保留。通过计算这些边界点之间的距离，判断两个分区的边界点是否是邻居。如果是邻居则加入map中。如0号分区和1号分区可得到(1，(-1，-1)，4))->(0，(0,0)，-1)，map的方向由后指向前，向前合并簇号，加入到map中。最后可得map为{(1，(-1，-1)，4))->(0，(0,0)，-1)，(3，(3,0)，-1)->(2,(2,0),-1)}

最后，每个分区都执行mapPartition()，每个样本根据合并map可得到最终的簇号，最后整合为一个分区后输出结果。

我们可根据上图数据集可划分成两个簇。通过上述的方法得到的聚类结果能够快速将数据分类到不同的类或者簇，所以同一个簇中的对象有很大的相似性，而不同簇间的对象有很大的相异性，能够快速区分哪些是噪声，哪些是有价值的数据。例如，此数据集如果是用户在淘宝购物的行为数据，我们可以根据最后的聚类结果，把用户归结成两组购物喜好的用户，比如一组用户喜好买衣服，可以更多的在用户购物时推荐衣服，另一组用户喜好买裤子，则可以更多的在用户购物时推荐裤子等。我们可以通过聚类结果实际情况挖掘出更多有价值的信息。