基于最大切削力的铣削瞬时切削力预测方法与流程

本发明涉及一种瞬时切削力预测方法，特别涉及一种基于最大切削力的铣削瞬时切削力预测方法。

背景技术：

文献“申请公布号是CN104268343A的中国发明专利”公开了一种端铣切削的瞬时切削力预测方法。该方法在分析端铣切削过程的基础上，建立基于平均切削力的铣削瞬时切削力预测方程，其中平均切削力表示为每齿进给和切削力系数的关系式；然后通过实验和回归分析的方法计算得到切削力系数，接着建立切削力系数关于切削速度、每齿进给量、轴向切深和径向切深的二次多项式；最后将切削力系数多项式代入端铣瞬时切削力预测方程，获得瞬时切削力预测模型。文献所述方法中切削力系数是基于实验获得的平均切削力计算求得，因而所建的“切削力模型对铣削力的变化趋势有较好的反映，但在数值上仍有一定的偏差”，并且该方法不能准确预测铣削瞬时最大切削力，预测的最大切削力误差为12.73％-32.31％。

技术实现要素：

为了克服现有瞬时切削力预测方法难以准确地预测铣削瞬时切削力及瞬时最大切削力的不足，本发明提供一种基于最大切削力的铣削瞬时切削力预测方法。该方法首先通过几何分析法确定铣刀第j个刀齿参与切削的切削接触角上、下限及刀齿参与切削的条件，构建铣削瞬时切削力关于切削力系数的预测方程；然后通过切削实验获得不同切削条件下的最大切削力，求解切削力系数，进而构建切削力系数关于切削参数的三次多项式；最后将切削力系数多项式代入铣削瞬时切削力预测方程，获得铣削瞬时切削力预测模型。本发明在构建铣削瞬时切削力预测模型时，采用三次多项式表示切削力系数关于切削参数的复杂关系，其中切削力系数是通过实验获得的瞬时最大切削力计算求得，因而能够更准确地预测铣削瞬时切削力及瞬时最大切削力。

本发明解决其技术问题所采用的技术方案：一种基于最大切削力的铣削瞬时切削力预测方法，其特点是包括以下步骤：

步骤一、建立铣削瞬时切削力预测方程。

1.将铣刀参与切削的区域沿着Z轴分解成等同于铣刀前角放置的刀片，作用在第j个刀齿上刀片的切向微元切削力dF_tj(θ)、径向微元切削力dF_rj(θ)和轴向微元切削力dF_aj(θ)，微元切削力计算公式如下：

式中，j＝1，2，…，m，m为铣刀齿数，K_t为切向切削力系数，K_r为径向切削力系数，K_a为轴向切削力系数，t_cj(θ)是铣刀旋转角θ时的径向瞬时切削层厚度，dz是刀片微元切削时的切削宽度。t_cj(θ)通过下式计算：

t_cj(θ)＝f_zsinθ (2)

d_z计算公式如下：

式中，f_z为每齿进给量，R为铣刀半径，α为铣刀螺旋角。

2.通过坐标变换，把切向、径向和轴向的微元切削力转换为x方向、y方向和z方向上的切削力，其公式为：

3.由于铣刀刀齿的相对均匀分布，切削力随着铣削过程呈现周期性变化，因此只需分析铣刀旋转角θ在0到之间的瞬时切削力变化。

顺铣切削：当铣刀刀齿旋转角为θ时，第j个刀齿切削接触角的上限和下限为：

式中，θ₀为径向接触角的补角，m为铣刀齿数，δ为滞后角。

逆铣切削：当铣刀刀齿旋转角为θ时，第j个刀齿切削接触角的上限和下限为：

式中，Ω为径向接触角。

对于铣削过程，第j个刀齿参与切削的条件是θ_l<θ_u。

由于铣刀呈螺旋状，这使得铣刀与工件上相对应的两点存在相对移动，铣刀上的点总是落后于工件上的对应点，滞后的角度δ与铣刀轴向切削深度a_p的关系，δ表示为：

Ω为铣削过程中铣刀和工件间的径向接触角，其公式为：

式中，a_w为切削宽度。

4.当铣刀旋转角为θ时，作用在第j个刀齿x方向、y方向和z方向切削力分别为F_xj(θ)、F_yj(θ)和F_zj(θ)，通过对微元切削力积分求得：

5.作用在铣刀上切削力的计算。

当铣刀旋转角为θ时，铣刀x方向，y方向和z方向切削力分别为F_x(θ)、F_y(θ)和F_z(θ)，通过对每齿切削力求和获得：

6.综合以上公式，铣削瞬时切削力预测方程表示为：

步骤二、基于最大切削力的切削力系数求解。

1.首先进行四因素三水平全因子实验设计，接着进行切削实验或切削仿真分析，获取不同实验组合下X、Y、Z三个方向切削力的最大值。

2.通过分析实验或切削仿真获取的瞬时切削力，获取X、Y和Z三个方向切削力最大值时的铣刀旋转角θ_xmax、θ_ymax和θ_zmax。

3.将上述求得的铣刀旋转角代入式(11)，即求得切削力最大值F_xmax、F_ymax和F_zmax与切削力系数的关系式如下：

4.将从切削实验或切削仿真分析获取的最大切削力代入式(12)，通过求解方程得到不同切削参数组合下的切削力系数K_t、K_r和K_a。

步骤三、构建切削力系数关于切削参数三次多项式。

1.切削力系数为关于切削速度、进给量、径向切宽和轴向切深的函数。由于切削力系数和切削参数间的关系复杂，不能简单的用线性函数表示，因此采用三次多项式来表示切削力系数和切削参数间复杂的函数关系，其公式如下：

式中，x₁为v的倒数，x₂为每齿进给量f_z，x₃为轴向切深a_p，x₄为径向切宽a_w的倒数，a_x、b_x、c_x为三次多项式系数，x＝0、i、ij、ijk。

2.根据步骤二获取的不同实验切削参数组合下的切削力系数K_t、K_r和K_a，采用最小二乘法，对式(13)中的未知参数a_x、b_x、c_x进行求解，从而建立切削力系数关于切削参数的三次多项式。

步骤四、构建铣削瞬时切削力预测模型。

将切削力系数三次多项式代入式(11)，获得铣削瞬时切削力预测模型。

式中，切削力系数K_t、K_r和K_a计算公式如式(13)，切削接触角上限θ_u、下限θ_l计算公式如式(5)和式(6)。

本发明的有益效果是：该方法首先通过几何分析法确定铣刀第j个刀齿参与切削的切削接触角上、下限及刀齿参与切削的条件，构建铣削瞬时切削力关于切削力系数的预测方程；然后通过切削实验获得不同切削条件下的最大切削力，求解切削力系数，进而构建切削力系数关于切削参数的三次多项式；最后将切削力系数多项式代入铣削瞬时切削力预测方程，获得铣削瞬时切削力预测模型。本发明在构建铣削瞬时切削力预测模型时，采用三次多项式表示切削力系数关于切削参数的复杂关系，其中切削力系数是通过实验获得的瞬时最大切削力计算求得，因而能够更准确地预测铣削瞬时切削力及瞬时最大切削力，预测的最大切削力误差由背景技术的12.73％-32.31％下降为2.2％-6.7％。

下面结合附图和具体实施方式对本发明作详细说明。

附图说明

图1是本发明方法的铣刀刀片微元铣削区域示意图；

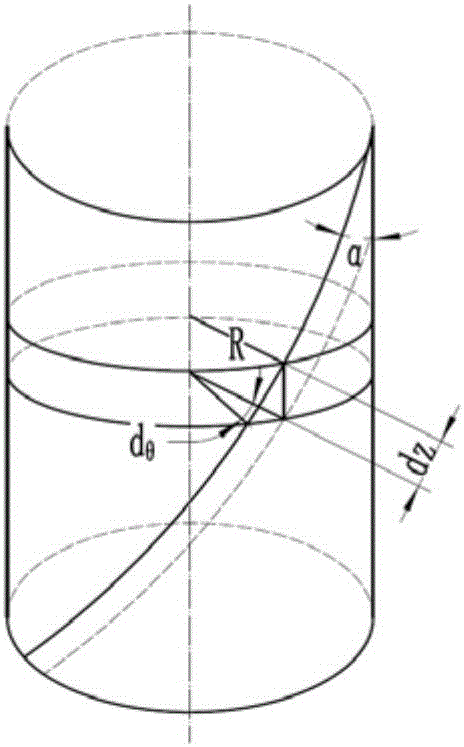
图2是本发明方法的铣刀旋转dθ时刀齿微元位置示意图；

图3是本发明方法的铣刀与工件顺铣切削接触示意图；

图4是本发明方法的铣刀与工件逆铣切削接触示意图；

图5是本发明方法的铣刀刀刃展开后角度示意图；

图6是本发明实施方式中第一组验证切削参数的预测瞬时切削力变化曲线；

图7是本发明实施方式中第一组验证切削参数的实验切削力变化曲线；

图8是本发明实施方式中第二组验证切削参数的预测瞬时切削力变化曲线；

图9是本发明实施方式中第二组验证切削参数的实验切削力变化曲线。

具体实施方式

参照图1-9。本发明基于最大切削力的铣削瞬时切削力预测方法具体步骤如下：

步骤一：铣削铝合金7050-T7451瞬时切削力预测方程建立。

1.将铣刀参与切削的区域沿着z轴分解成等同于铣刀前角放置的刀片，作用在第j个刀齿上刀片的切向微元切削力dF_tj(θ)、径向微元切削力dF_rj(θ)和轴向微元切削力dF_aj(θ)，微元切削力计算公式如下：

式中，j＝1，2，3，K_t为切向切削力系数，K_r为径向切削力系数，K_a为轴向切削力系数，t_cj(θ)是铣刀旋转角θ的径向瞬时切削层厚度，dz是刀片微元切削时的切削宽度。t_cj(θ)通过下式计算：

t_cj(θ)＝f_zsinθ (2)

d_z计算公式如下：

式中，f_z为每齿进给量，R为铣刀半径4mm，α为铣刀螺旋角30°。

2.通过坐标变换，把切向、径向和轴向的微元切削力转换为x方向、y方向和z方向上的切削力，其公式为：

3.由于铣刀刀齿的相对均匀分布，切削力随着铣削过程呈现周期性变化，因此只需分析铣刀旋转角θ在0到之间的瞬时切削力变化。

顺铣切削：当铣刀刀齿旋转角为θ时，第j个刀齿切削接触角的上限和下限为：

式中，θ₀为径向接触角的补角，m为铣刀齿数3，δ为滞后角。

逆铣切削：当铣刀刀齿旋转角为θ时，第j个刀齿切削接触角的上限和下限为：

式中，Ω为径向接触角。

对于铣削过程，第j个刀齿参与切削的条件是θ_l<θ_u。

由于铣刀呈螺旋状，这使得铣刀与工件上相对应的两点存在相对移动，铣刀上的点总是落后于工件上的对应点，滞后的角度δ与铣刀轴向切削深度a_p的关系，δ表示为：

Ω为铣削过程中铣刀和工件间的径向接触角，其公式为：

式中，a_w为切削宽度。

4.当铣刀旋转角为θ时，作用在第j个刀齿x方向、y方向和z方向切削力分别为F_xj(θ)、F_yj(θ)和F_zj(θ)，通过对微元切削力积分求得：

5.当铣刀旋转角为θ时，铣刀x方向，y方向和z方向切削力分别为F_x(θ)、F_y(θ)和F_z(θ)，通过对每齿切削力求和获得：

6.综合以上公式，铣削瞬时切削力预测方程表示为：

步骤二：通过切削实验获取切削力最大值，进而求解切削力系数。

1.切削实验条件：

1)切削实验平台：北京精雕JDLVG600_A10P型数控加工中心。

2)实验材料：美国ALCOA铝合金7050-T7451薄板。

3)铣刀：高速整体硬质合金立铣刀，立铣刀直径8mm，齿数3，螺旋角30°。

4)切削力测量系统：将工件固定在Kistler 9255B测力仪上面，测力仪放置在机床工作台上，测力仪连接Kistler 5070A电荷放大器，电荷放大器连接Kistler 5697A1数据采集器，数据采集器连接电脑。

2.实验设计：

为构建切削力系数关于切削参数的三次多项式，设计四因素三水平全因子实验。实验的因素水平见表1。

表1全因子实验因素水平表

3.实验结果：

根据81组不同的切削参数组合，进行顺铣切削实验，获取切削力最大值，见表2。

表2最大切削力

4.通过分析实验获取的瞬时切削力，获取X、Y和Z三个方向切削力最大值时的铣刀旋转角θ_xmax、θ_ymax和θ_zmax，其结果见表3。

表3切削力最大值时的铣刀旋转角

5.将上述求得的刀具旋转角代入式(11)，求得切削力最大值F_xmax、F_ymax和F_zmax与切削力系数的关系式如下：

6.将表2中最大切削力代入式(12)，计算得到不同实验切削参数组合下的切削力系数K_t、K_r和K_a，结果见表4。

表4切削力系数

步骤三：构建切削力系数关于切削参数的三次多项式。

构建切削力系数K_t、K_r和K_a关于切削参数的三次多项式如下：

式中，x₁为v的倒数，x₂为每齿进给量f_z，x₃为轴向切深a_p，x₄为径向切宽a_w的倒数，a_x、b_x、c_x为三次多项式系数，x＝0、i、ij、ijk。

根据表4中的切削力系数，采用最小二乘法，求得式(13)中的未知参数a_x、b_x、c_x，结果见表5，从而获得切削力系数多项式。

表5切削力系数K_t、K_r和K_a系数回归

步骤三：将切削力系数多项式代入式(11)，完成铣削瞬时切削力预测模型的构建，其模型如下：

式中，切削力系数K_t、K_r、和K_a计算如式(13)，式(13)中，a_x、b_x、c_x为多项式系数见表5，x＝0、i、ij、ijk。

步骤四：通过与切削实验结果对比分析，验证所构建的铣削瞬时切削力预测模型。

选取切削参数见表6，可根据切削力系数多项式(13)计算切削力系数K_t、K_r和K_a，接着将各参数代入式(14)顺铣瞬时切削力预测模型，即可获得铣削瞬时切削力F_x、F_y和F_z。

表6切削参数表

从图6和图8预测的瞬时切削力变化曲线以及图7和图9实验切削力变化曲线可以看出，所建的切削力预测模型能够较好的预测瞬时切削力，预测的瞬时最大切削力与实验的瞬时最大切削力的对比结果见表7，误差在2.2％-6.7％之间。

表7瞬时最大切削力

由此说明，本发明基于最大切削力的铣削瞬时切削力预测方法能够准确地预测铣削瞬时切削力及瞬时最大切削力。