一种输出中高频响应的车‑轨‑桥耦合振动频域模型的制作方法

本发明涉及一种输出中高频响应的车-轨-桥耦合振动频域模型，可应用于高架轨道交通车辆、轨道及桥梁结构中、高频振动响应的预测，模型输出的上述中高频响应可作为轨道交通环境振动及噪声预测的激励源，进而为研究轨道交通环境振动及噪声问题提供理论支持。

背景技术：

随着社会经济的发展和城市化进程的不断推进，交通问题日益突出。轨道交通作为一种大容量交通运输工具，能有效解决客流大密度出行问题，对经济发展的推动作用不容忽视。轨道交通高架线路由于建设周期短、费用低，具有很好的线路平顺性和稳定性，同时可以更为可靠地控制地基长期沉降等优点，在整个轨道交通线路中占有很大比例。但是，高架轨道交通车辆运行引起的环境振动问题及噪声辐射问题却在某种程度上降低了它的优势。随着人们生活水平的提高，公众对振动和噪声问题的容忍度不断降低，并由此引发了诸多社会问题。

轨道交通车辆在运行过程中，钢轨表面和车轮踏面之间的组合不平顺引起动态轮轨力，动态轮轨力向上传递给列车引起车辆振动，向下传递给轨道致使轨道结构振动，轨道结构的振动再经由轨道支承系统传递给桥梁结构，进而引发桥梁结构的振动和噪声辐射问题。因而，准确建立车-轨-桥耦合振动分析模型，探明车-轨-桥耦合系统中振动能量的产生和传递机理对控制高架轨道交通环境振动及噪声问题具有重要作用。

传统的对车-轨-桥耦合系统进行建模和动力分析时通常建立时域模型，但时域模型主要用于分析列车运行时桥梁结构的强度，关注的桥梁结构振动频率通常低于20Hz，然而，高架轨道交通环境振动问题关注的振动频率范围为1～80Hz，而高架轨道交通噪声问题关注的频率范围则更高，若采用时域方法建立车-轨-桥耦合振动分析模型，则输出的响应难以用于对轨道交通环境振动及噪声进行准确预测。

因此，提出一种输出中高频响应的车-轨-桥耦合振动频域模型至关重要，通过该模型计算输出的响应更适合于高架轨道交通环境振动及噪声预测，该方法能够揭示车-轨-桥结构振动和能量产生与传递的机理及影响规律，从而为有针对性的采取减振降噪措施提供理论依据。

技术实现要素：

本发明的目的是提出一种输出中高频响应的车-轨-桥耦合振动频域模型，解决传统的对车-轨-桥耦合系统进行建模和动力分析时通常建立时域模型，但时域模型主要用于分析列车运行时桥梁结构的强度，关注的桥梁结构振动频率通常低于20Hz，然而，高架轨道交通环境振动问题关注的振动频率范围为1～80Hz，而高架轨道交通噪声问题关注的频率范围则更高，若采用时域方法建立车-轨-桥耦合振动分析模型，则输出的响应难以用于对轨道交通环境振动及噪声进行准确预测的问题。

本发明解决其技术问题所采用的技术方案为：

一种输出中高频响应的车-轨-桥耦合振动频域模型，包括以下几个步骤：

第一步、选取车-轨-桥耦合振动仿真预测所包含的车辆参数、轨道结构参数、轮轨组合粗糙度谱、桥梁结构参数及行车速度参数；

第二步、根据步骤(一)所选的车辆参数，建立10个自由度的车辆模型，且沿纵向的1/2车体、1/2转向架和车轮均考虑为刚体，考虑车体和转向架的沉浮、点头自由度以及车轮的沉浮自由度；

通过逐一对各刚体应用D′Alembert原理，并根据车辆系统运动方程表达式：

其中，M、C和K分别为车辆系统的质量、阻尼和刚度矩阵，z为车辆系统的自由度向量，F为作用在车辆系统上的外力；

在频域求解车辆系统的稳态响应，令z＝Z(ω)e^iωt，可通过车辆运动方程求解车辆系统频域响应Z(ω)，进而根据位移导纳定义，可求得车轮位移导纳，其数学表达式为

式中F_j表示第j个轮轨接触点位置时的轮轨力，表示当轮轨力F_j作用于第j个轮轨接触点位置时第i个轮轨接触点处车轮的响应，N_w表示轮轨接触点的总数；导纳表示单位力作用于第j个轮轨接触点位置时第i个轮轨接触点处车轮的响应；钢轨上作用N_w个车轮，则车轮导纳可写成一个N_w×N_w的矩阵，其表达式为：

上式中，N_w即为轮轨接触点的总数；

第三步、再根据步骤(一)所选的轨道结构参数和桥梁结构参数，建立四层叠合梁模拟轨-桥耦合子系统；

第四步、然后根据步骤(一)所选轮轨组合粗糙度谱及车轮和钢轨的参数，建立轮轨相互作用模型，轮轨接触弹簧即为车轮粗糙度弹簧和轨道粗糙度弹簧串联得到，则其刚度满足

式中K_C为轮轨接触弹簧刚度，K_CR为轨道粗糙度弹簧刚度，K_CW为车轮粗糙度弹簧刚度；

即可得到轮轨接触弹簧导纳为α_C＝1/K_C

同时可得轮轨接触弹簧导纳矩阵为

第五步、根据车-轨-桥耦合模型涉及的多个轮轨耦合作用，建立轮轨耦合模型叠加法，根据叠加法原理，首先设定仅第一车轮(1)与轨道之间存在不平顺激励，产生的轮轨力称为主动力P₁₁，在第二车轮(2)、第三车轮(3)和第四车轮(4)与轨道接触点产生的力分别为被动力P₂₁、P₃₁和P₄₁，将轮轨接触点的第二轮轨接触点(6)、第三轮轨接触点(7)和第四轮轨接触点(8)分别视为主动激励点，类推可得到第k个轮轨接触点激励作用下的第j个接触点处的主动力与被动力，其计算表达式为：

式中P_jk表示当激励作用于k点时j点处产生的力，N_w为轮轨接触点的个数，F_wrj表示第j个轮轨接触点处的动态轮轨力；

因此可以得出轮轨作用力，以数学表达式以向量的形式表示为

F_wr＝{F_wrj} j＝1,2,...,N_w

式中：N_w为轮轨接触点的个数，F_wr表示各轮轨接触点的动态轮轨力向量，F_wrj表示第j个轮轨接触点处的动态轮轨力。

第六步、根据车轮模型轴距和定距的存在，不同轮轨接触点之间的激励出现时间滞后关系，其轮轨接触点的不平顺的数学表达式为

式中，Δ(ω)为N_w个轮轨接触点处的轮轨粗糙度向量，△₁(ω)为第1个轮轨接触点处的轮轨粗糙度值，i为虚数单位，ω为圆频率，t_i为第i个轮轨接触点与第1个轮轨接触点之间由于距离的存在产生的时间差。

第七步、根据步骤(二)得到的车轮导纳矩阵α^w、步骤(三)得到的轨道结构导纳矩阵α^R、步骤(四)得到的轮轨接触弹簧导纳矩阵α^C、步骤(五)得到多轮轨相互作用的动态轮轨力关系以及步骤(六)中的N_w个轮轨接触点处的不平顺向量Δ(ω)，可求得动态轮轨力，其数学表达式为

F_wr(ω)＝-(α^w+α^R+α^C)^-1Δ(ω)

式中，F_wr(ω)为各轮轨接触点处的动态轮轨力向量；α^w为车轮导纳矩阵；α^R为轨道的钢轨导纳矩阵；为轮轨接触导纳矩阵；Δ(ω)＝{△_j}，j＝1,2,...,N_w为轮轨接触点的轨道粗糙度向量。

第八步、将步骤(七)得到的动态轮轨力作为激励力，施加到步骤(二)中的车辆运动方程中及步骤(三)中的轨-桥耦合模型运动方程中进一步求得车辆、轨道结构及桥梁结构的频域位移响应Z(ω)。

第九步、根据速度及加速度与位移之间的关系式，进一步求得车辆、轨道结构及桥梁结构的速度及加速度频域响应；其数学表达式为：

式中，i为虚数单位，ω为圆频率，Z(ω)表示频率位移响应，表示频率速度响应，表示频率加速度响应。

采用本发明的技术方案，采用一种输出中高频响应的车-轨-桥耦合振动频域模型，首先，选取车-轨-桥耦合振动仿真预测参数，将其输入车-轨-桥耦合模型中，根据车辆动力学方程及轨道-桥梁耦合模型分别求解车轮导纳矩阵、轨道导纳矩阵，根据轮轨相互作用模型求解轮轨接触弹簧导纳矩阵；将求得的车轮导纳矩阵、轨道导纳矩阵和轮轨接触弹簧导纳矩阵代入动态轮轨力公式求得动态轮轨力；最后将求得的动态轮轨力代入车辆运动方程、轨道-桥梁耦合模型运动方程作为车辆模型和轨道-桥梁耦合模型的激励源，进一步求解动态轮轨力引起的车辆、轨道和桥梁结构频域动力响应；该方法能够揭示车-轨-桥结构振动和能量产生与传递的机理及影响规律，从而为有针对性的采取减振降噪措施提供理论依据。

与现有技术相比，本发明的有益效果是，从车-轨-桥耦合系统振动产生的机理出发，先求解动态轮轨力频谱，再以动态轮轨力作为激励求解车辆、轨道、桥梁结构的频域动力响应；研究关注的频段范围为20～500Hz，属于中高频段，输出的系统响应可用于进一步研究高架轨道交通环境振动和噪声问题，与现有常规的车-轨-桥耦合振动时域模型相比，一是更加准确地考虑了动态轮轨力的中高频激励影响；二是避开时域方法所须采用的分步积分，计算效率大大提高，同时频域结果保证了满足工程要求的计算精度；三是该预测模型适用性强，能应用与不同的车辆类型、轨道结构类型、桥梁结构类型。此外，由于该模型计算输出的响应可作为高架轨道交通环境振动和噪声问题的激励源，通过对该模型的参数研究，从而指导轨道形式选择及桥梁结构设计，对高架轨道交通环境振动及噪声控制具有重要理论意义。

综上所述，采用本发明的一种输出中高频响应的车-轨-桥耦合振动频域模型可以解决传统的对车-轨-桥耦合系统进行建模和动力分析时通常建立时域模型，但时域模型主要用于分析列车运行时桥梁结构的强度，关注的桥梁结构振动频率通常低于20Hz，然而，高架轨道交通环境振动问题关注的振动频率范围为1～80Hz，而高架轨道交通噪声问题关注的频率范围则更高，若采用时域方法建立车-轨-桥耦合振动分析模型，则输出的响应难以用于对轨道交通环境振动及噪声进行准确预测的问题。

附图说明

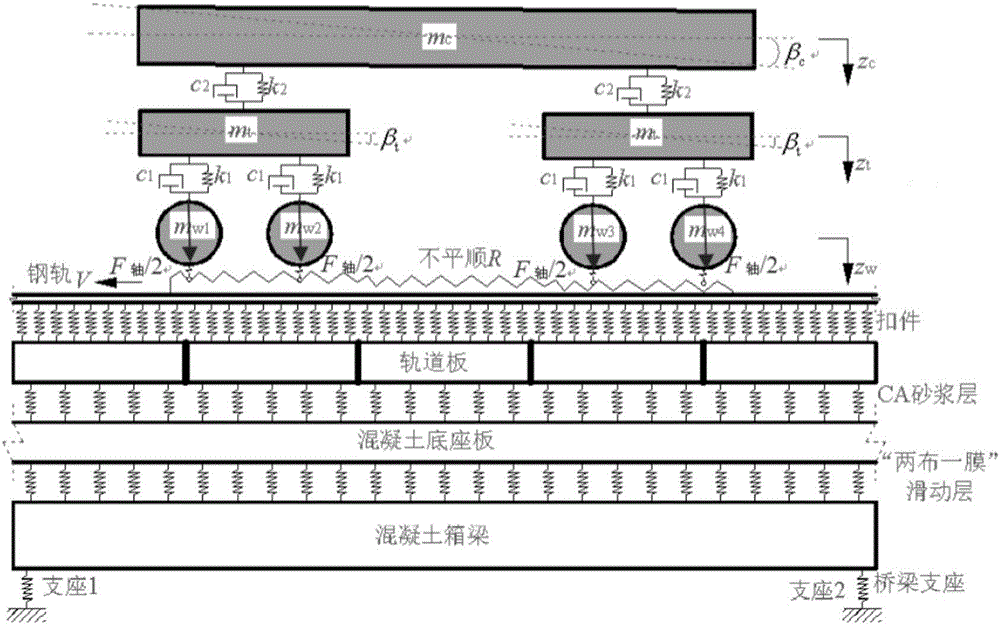
图1为本发明的车-轨-桥耦合振动分析模型；

图2为本发明的四层叠合梁模拟的轨-桥耦合模型；

图3为本发明的Remington轮轨相互作用模型；

图4为本发明的多车轮作用情况下的轮轨耦合模型叠加法；

图5为本发明的车-轨-桥耦合模型建模流程图；

图6为本发明的列车过桥照片；

图7为本发明的直线桥梁段CRTSⅡ型板式无砟轨道横截面示意图；

图8为本发明的32m双线混凝土简支箱梁典型横截面图；

图9为本发明的京沪高铁实测轨道不平顺谱；

图10为本发明的第一车轮位置处作用单位力时的车轮导纳；

图11为本发明的第二车轮位置处作用单位力时的车轮导纳；

图12为本发明的第三车轮位置处作用单位力时的车轮导纳；

图13为本发明的第四车轮位置处作用单位力时的车轮导纳；

图14为本发明的第一车轮位置处作用单位力时的轨道结构导纳；

图15为本发明的第二车轮位置处作用单位力时的轨道结构导纳；

图16为本发明的第三车轮位置处作用单位力时的轨道结构导纳；

图17为本发明的第四车轮位置处作用单位力时的轨道结构导纳；

图18为本发明的各轮轨接触点处的动态轮轨力幅值和相位；

图19各车速下车辆加速度幅值对比；

图20各车速下桥梁跨中加速度的幅值对比；

图21为F轴/2示意图。

具体实施方式

下面结合附图和实施例对本发明的技术方案作进一步说明。

如图1～21所示，一种输出中高频响应的车-轨-桥耦合振动频域模型，包括以下几个步骤：

第一步、选取车-轨-桥耦合振动仿真预测所包含的车辆参数、轨道结构参数、轮轨组合粗糙度谱、桥梁结构参数及行车速度参数；

第二步、根据步骤(一)所选的车辆参数，建立10个自由度的车辆模型，且沿纵向的1/2车体、1/2转向架和车轮均考虑为刚体，考虑车体和转向架的沉浮、点头自由度以及车轮的沉浮自由度；

通过逐一对各刚体应用D′Alembert原理，并根据车辆系统运动方程表达式：

其中，M、C和K分别为车辆系统的质量、阻尼和刚度矩阵，z为车辆系统的自由度向量，F为作用在车辆系统上的外力；

在频域求解车辆系统的稳态响应，令z＝Z(ω)e^iωt，可通过车辆运动方程求解车辆系统频域响应Z(ω)，进而根据位移导纳定义，可求得车轮位移导纳，其数学表达式为

式中，F_j表示第j个轮轨接触点位置时的轮轨力，表示当轮轨力F_j作用于第j个轮轨接触点位置时第i个轮轨接触点处车轮的响应；导纳表示单位力作用于第j个轮轨接触点位置时第i个轮轨接触点处车轮的响应；若钢轨上作用N_w个车轮，则车轮导纳可写成一个N_w×N_w的矩阵，其表达式为：

式中，N_w即为轮轨接触点的总数；

第三步、再根据步骤(一)所选的轨道结构参数和桥梁结构参数，建立四层叠合梁模拟轨-桥耦合子系统；

第四步、然后根据步骤(一)所选轮轨组合粗糙度谱及车轮和钢轨的参数，建立轮轨相互作用模型，轮轨接触弹簧即为车轮粗糙度弹簧和轨道粗糙度弹簧串联得到，则其刚度满足

式中K_C为轮轨接触弹簧刚度，K_CR为轨道粗糙度弹簧刚度，K_CW为车轮粗糙度弹簧刚度；

即可得到轮轨接触弹簧导纳为α_C＝1/K_C

同时可得轮轨接触弹簧导纳矩阵为

式中，为N_w阶单位阵。

第五步、根据车-轨-桥耦合模型涉及的多个轮轨耦合作用，建立轮轨耦合模型叠加法，根据叠加法原理，首先设定仅第一车轮1与轨道之间存在不平顺激励，产生的轮轨力称为主动力P₁₁，在第二车轮2、第三车轮3和第四车轮4与轨道接触点产生的力分别为被动力P₂₁、P₃₁和P₄₁，将轮轨接触点的第二轮轨接触点(6)、第三轮轨接触点(7)和第四轮轨接触点(8)分别视为主动激励点，类推可得到N_w个轮轨接触点时，第k个轮轨接触点激励作用下的第j个轮轨接触点处的总轮轨力，其计算表达式为：

式中N_w为轮轨接触点个数，P_jk表示当激励作用于k点时j点处产生的相互作用力，F_wrj表示第j个轮轨接触点处的动态轮轨力；

因此可以得出轮轨作用力，以数学表达式以向量的形式表示为

F_wr(ω)＝{F_wrj} j＝1,2,...,N_w

式中F_wr(ω)表示N_w个轮轨接触点的动态轮轨力向量；

第六步、由于车轮模型轴距和定距的存在，不同轮轨接触点之间的激励存在时间滞后关系，各轮轨接触点粗糙度的数学表达式为

式中Δ(ω)表示各个轮轨接触点处的轮轨粗糙度向量，△₁(ω)表示第1个轮轨接触点处的轮轨粗糙度值，为虚数单位，ω为圆频率，t_i为第i个轮轨接触点与第1个轮轨接触点间距离产生的时间差。

第七步、根据步骤(二)得到的车轮导纳矩阵α^w、步骤(三)得到的轨道结构导纳矩阵α^R、步骤(四)得到的轮轨接触弹簧导纳矩阵α^C、步骤(五)得到多轮轨相互作用的动态轮轨力关系以及步骤(六)中的N_w个轮轨接触点处的不平顺向量Δ(ω)，可求得动态轮轨力F_wr(ω)，其数学表达式为

F_wr(ω)＝-(α^w+α^R+α^C)^-1Δ(ω)

式中，F_wr(ω)动态轮轨力向量；α^w为车轮导纳矩阵；α^R为轨道的钢轨导纳矩阵；α^C＝I_Nw×Nwα_c为轮轨接触导纳矩阵，Δ(ω)＝{△_j}，j＝1,2,...,N_w为轮轨接触点的轨道不平顺向量。

第八步、将步骤(七)得到的动态轮轨力作为激励力，施加到步骤(二)中的车辆运动方程中及步骤(三)中的轨-桥耦合模型运动方程中进一步求得车辆、轨道结构及桥梁结构的频域位移响应Z(ω)。

第九步、根据速度及加速度与位移之间的关系式，进一步求得车辆、轨道结构及桥梁结构的速度及加速度频域响应。其数学表达式为：

式中，i为虚数单位，ω为圆频率，Z(ω)表示频率位移响应，表示频率速度响应，表示频率加速度响应。

试验时以某客运专线高速列车通过32m混凝土简支箱梁桥为例，高速列车过桥如图6所示，给出本发明方法对车-轨-桥耦合振动仿真预测的具体过程。

(1)确定车-轨-桥耦合振动仿真预测参数，主要为列车类型(CRH380A)及相关参数。如表1所示、轨道结构类型(CRTSⅡ型版式无砟轨道如图7所示)、桥梁结构类型(32m混凝土简支箱梁如图8所示)及相关参数如表2所示、轮轨粗糙度谱参数(采用京沪高铁实测轨道谱如图9所示)、车辆运行速度(350km/h)。

其参数如下表所示：

表1 车辆动力学参数(单根钢轨上支承的车辆)

表2 4层叠合梁模拟的轨道-桥梁耦合模型动力学参数

(2)将车辆模型参数如表1所示，代入车辆运动方程首先求出车轮导纳矩阵，得到车轮导纳如图10～13所示。

(3)将轨-桥耦合模型参数如表2所示，代入轨-桥耦合振动方程求出轨道结构导纳矩阵，得到轨道结构导纳如图14～17所示。

(4)将车轮、钢轨参数代入轮轨接触弹簧导纳计算式，求得轮轨接触弹簧导纳矩阵。

(5)将车轮导纳矩阵、轨道结构导纳矩阵和轮轨接触弹簧导纳矩阵以及轮轨粗糙度谱参数代入动态轮轨力计算式，求出轮轨接触点处的动态轮轨力，如图18所示。

(6)将上一步求得的动态轮轨力作为激励力输入车辆运动方程和轨-桥耦合运动方程，进而求得车辆系统动力响应如图19所示和桥梁结构动力响应如图20所示。

其具体计算方法包括如下步骤：

(1)明确车-轨-桥耦合振动频域模型预测参数，所述预测参数包括车辆参数、轨道结构参数、轮轨组合粗糙度谱、桥梁结构参数及行车速度；如下表所示：

表1 车辆动力学参数(单根钢轨上支承的车辆)

表2 4层叠合梁模拟的轨道-桥梁耦合模型动力学参数

(2)根据步骤(1)所选的车辆参数，建立如图21所示单根钢轨上作用如图1所示10个自由度的车辆模型，沿纵向的1/2车体、1/2转向架和车轮均考虑为刚体，考虑了车体和转向架的沉浮、点头自由度以及车轮的沉浮自由度。

通过逐一对各刚体应用D’Alembert原理，可得车辆系统运动方程为：

其中，M、C和K分别为车辆系统的质量、阻尼和刚度矩阵，z为车辆系统的自由度向量，F为作用在车辆系统上的外力，其具体表达式如下

z＝{z_c β_c z_t1 β_t1 z_t2 β_t2 z_w1 z_w2 z_w3 z_w4}^T (2)

F＝{0 0 0 0 0 0 -F_wr1 -F_wr2 -F_wr3 -F_wr4}^T (3)

M＝diag(m_c,I_c.m_b,I_b,m_b,I_b,m_w,m_w,m_w,m_w) (4)

以上车辆模型共考虑了10个独立自由度，分别为z_c,β_c,z_t1,β_t1,z_t2,β_t2,z_w1,z_w2,z_w3,z_w4，其中z代表沉浮自由度、β代表点头自由度，下标c代表车体，t1和t2分别代表前后两个转向架，w1～w4分别代表4个车轮。m_c、m_t和m_w分别为1/2车体、1/2转向架和车轮质量，I_c、I_t分别为1/2车体和1/2转向架的点头转动惯量，k₁、k₂、c₁和c₂分别为车辆一系、二系悬挂系统刚度、阻尼系数，L_t为车辆定距之半，L_w分车辆轴距之半，L_c为车辆钩到钩的距离。

在频域求解车辆系统的稳态响应，令z＝Z(ω)e^iωt，可通过车辆运动方程求解车辆系统频域响应Z(ω)。如图1所示有4个轮轨接触点时，根据位移导纳定义，可求得车轮位移导纳为

式中，表示当轮轨力F_j作用于第j个轮轨接触点位置时，第i个轮轨接触点处车轮的响应；导纳表示单位力作用于第j个轮轨接触点位置时，第i个轮轨接触点处车轮的响应。如图1所示有4个轮轨接触点时，则车轮导纳可写成一个4×4的矩阵

(3)根据步骤(1)所选的轨道结构参数和桥梁结构参数，建立四层叠合梁模拟模拟轨-桥耦合子系统，如图2所示。四层叠合梁由上到下分别模拟钢轨、轨道板、底座板和桥梁，各层梁之间通过弹性支承进行联结，共包括四层弹性支承，由上到下分别表示扣件层、CA砂浆层、“两布一膜”滑动层和桥梁支座。为方便描述，钢轨、轨道板、底座板和箱梁的单位长度质量、抗弯刚度和损耗因子分别记为m、EI和η，并以下标“r”、“s”、“d”和“b”分别表示钢轨、轨道板、底座板和箱梁；跨度L范围内有n_s块长度为L_s的轨道板，不计相邻轨道板间距；弹性支承弹簧刚度、损耗因子和间距分别记为k、η和d，并以下标“f”、“c”、“h”和“bs”分别表示钢轨扣件、CA砂浆层、“两布一膜”滑动层和桥梁支座，需指出的是d_bs表示桥梁支座距离箱梁最近梁端距离(沿纵向)；每块轨道板上部和下部的离散弹簧数目分别记为N_sf和N_sc，每跨箱梁跨度L范围内的扣件、CA砂浆层、“两布一膜”滑动层和桥梁支座离散弹簧总数分别记为n_f、n_c、n_h和n_bs，则应满足n_f＝n_s×N_sf和n_c＝n_s×N_sc。根据轨道结构的几何参数，其应满足关系式L＝n_s×L_s和L_s＝N_sf×d_f＝N_sc×d_c。

建立如图2所示的xoz坐标系，坐标原点o位于叠合梁单元左端端点处。钢轨扣件弹簧的坐标记为x_fi，i＝1,…，n_f；CA砂浆层弹簧的坐标记为x_ci，i＝1,…，n_c；“两布一膜”滑动层弹簧的坐标记为x_hi，i＝1,…，n_h；桥梁支座弹簧的坐标记为x_bsi，i＝1,…，n_bs。第h块轨道板上部和下部弹簧的局部坐标分为记为和h＝1,…,n_s；i＝1,…,N_sf；j＝1,…,N_sc。对于扣件总体坐标系坐标x_fm与局部坐标系坐标当m＝(h-1)×N_sf+n时，坐标x_fm和对应同一个钢轨扣件；对于CA砂浆层弹簧总体坐标系坐标x_cm与局部坐标系坐标当m＝(h-1)×N_sc+n时，坐标x_cm和对应同一个CA砂浆层弹簧。

对轨道结构中各层叠合梁分别取出进行分析，各层叠合梁的垂向振动位移响应与其上作用的荷载激励有关，根据叠加原理，各层梁体的垂向振动响应由各荷载激励引起的振动响应叠加得到。结合导纳法的思想，钢轨、轨道板、底座板和桥梁的垂向位移响应可分别表示为

式(9)～(12)中，G_r(x,x_P)、G_s(x,x_P)、G_d(x,x_P)和G_b(x,x_P)分别表示钢轨、轨道板、底座板和桥梁在x_P处作用单位1的激励时x处的位移响应，即为各层梁体的位移导纳函数；F为钢轨上作用的外荷载激励；P_fi表示钢轨下部第i个扣件的扣件力；分别表示第h块轨道板上部的第j个扣件力和下部的第k个CA砂浆层弹性支承力；P_ci、P_hi分别表示底座板上部的第i个CA砂浆层弹性支承力和下部的第i个滑动层弹性支承力；P_bsi表示桥梁下部的第i个支座反力。

钢轨扣件力P_fi或CA砂浆层弹性支承力P_ci或滑动层弹性支承力P_hi和桥梁支座反力P_bsi可由其自身复刚度与其变形量的乘积求得。

对于钢轨扣件力，当i＝(h-1)×N_sf+j时，P_fi和对应同一扣件的扣件力，可表示为

式中，i＝1,2,…,n_f；h＝1,2,…，n_s；j＝1,2,…，N_sf。

对于CA砂浆层弹性支承力，当i＝(h-1)×N_sc+k时，P_ci和对应同一CA砂浆层弹性支承力，可表示为

式中，i＝1,2,…,n_c；h＝1,2,…，n_s；k＝1,2,…，N_sc。

滑动层弹性支承力P_hi可表示为

P_hi＝k_h(1+iη_h)[Z_d(x_hi)-Z_b(x_hi)]，i＝1,2,…,n_h (15)

桥梁支座反力P_bsi可表示为

P_bsi＝k_bs(1+iη_bs)Z_b(x_bsi)，i＝1,…,n_bs (16)

由式(9)～式(12)求出式(13)～式(16)中钢轨、轨道板、底座板和桥梁在各弹性支承点处的位移响应，可表示为

将式(17)～(23)代入式(13)～(16)后可得到

i＝1,2,…,n_f且i＝(h-1)×N_sf+j，h＝1,2,…，n_s，j＝1,2,…，N_sf

i＝1,2,…,n_c且i＝(h-1)×N_sc+k,h＝1,2,…，n_s,k＝1,2,…，N_sc

将式(24)等号右端第2～4项移到方程左端，同时将式(25)～(27)等号右端项均移到方程左端，经整理将各方程合并写成矩阵形式得

[A(ω)]{P}＝{U} (28)

式中，[A(ω)]为由钢轨、轨道板、底座板和桥梁的位移导纳以及钢轨扣件、CA砂浆层、滑动层和支座的刚度、阻抗参数等构成的(n_f+n_c+n_h+n_bs)×(n_f+n_c+n_h+n_bs)维动柔度矩阵；{P}为由钢轨扣件力、CA砂浆层弹性支承力、滑动层弹性支承力和桥梁支座反力等组成的(n_f+n_c+n_h+n_bs)维待求列向量；{U}为外荷载激励引起的各层叠合梁各弹性支承处的(n_f+n_c+n_h+n_bs)维位移响应，其中仅前n_f个元素非0，为FG_r(x_fi,x_F)，i＝1,2,…,n_f，其余元素为0。

由式(28)求出轨道桥梁耦合系统中各弹性支承力及支座反力列向量{P}，将其代入式(9)计算钢轨上任意位置处由外荷载F作用引起的位移响应Z_r(x_i)。该响应与外荷载F的比值即为轨-桥耦合系统的位移导纳，记为

上式中，表示钢轨上x_j处单位力，引起钢轨上x_i处的位移响应。当i＝j时，为钢轨位移点导纳，当i≠j时，为钢轨位移传递导纳。

如图1所示有4个轮轨接触点时，则轨道结构的钢轨位移导纳矩阵为

(4)根据步骤(1)所选轮轨组合粗糙度谱及车轮和钢轨等的参数，建立轮轨相互作用模型，如图3所示，轮轨接触弹簧即为车轮粗糙度弹簧和轨道粗糙度弹簧串联得到，则其刚度满足

式中，K_C为轮轨接触弹簧刚度，K_CR为轨道粗糙度弹簧刚度，K_CW为车轮粗糙度弹簧刚度。

轮轨接触弹簧导纳即为α_C＝1/K_C

如图1所示有4个轮轨接触点时，则可得轮轨接触弹簧导纳矩阵为

α^C＝I_4×4α_C (32)

(5)如图1所建立的车-轨-桥耦合模型涉及多个轮轨耦合作用，建立轮轨耦合模型叠加法示意图，如图4所示。由图4可知，根据叠加法原理，首先设定仅车轮1与轨道之间存在不平顺激励，由其产生的轮轨力称为主动力P₁₁，在其余车轮2、3、4与轨道接触点产生的力称为被动力P₂₁、P₃₁、P₄₁，此处的P_jk表示当激励作用于k点时j点处产生的力。同理，将轮轨接触点2、3、4分别视为主动激励点，可得到各轮轨接触点激励作用下的各接触点处的主动力与被动力。通过叠加，可得到各轮轨接触处总的轮轨作用力

轮轨作用力以向量的形式表示，有

F_wr＝{F_wrj} j＝1,2,3,4 (34)

(6)由于车轮模型轴距和定距的存在，不同轮轨接触点之间的激励出现时间滞后关系，图4模型中4个轮轨接触点的不平顺可表示为

Δ(t)＝{△₁(t-t₁) △₂(t-t₂) △₃(t-t₃) △₄(t-t₄)}^T (35)

式中，设定t₁＝0，则t₂＝2l_w/V，t₃＝2l_b/V，t₄＝2(l_b+l_w)/V为各车轮与车轮1之间的时间差。其中，V为车速，l_w和l_b分别为车轮轴距和定距之半。

假设时域的轨道不平顺为△(t)＝△(ω)e^iωt，则可得

(7)根据步骤(2)得到的车轮导纳矩阵α^w、步骤(3)得到的轨道结构导纳矩阵α^R、步骤(4)得到的轮轨接触弹簧导纳矩阵α^C、步骤(5)得到多轮轨相互作用的动态轮轨力关系以及步骤(6)中的N_w个轮轨接触点处的不平顺向量Δ(ω)，可求得动态轮轨力为

F_wr＝-(α^w+α^R+α^C)^-1Δ (37)

式中，α^w为车轮导纳矩阵；α^R为轨道的钢轨导纳矩阵；α^C＝I_4×4α_c为轮轨接触导纳矩阵，Δ＝{△_j}，j＝1,2,3,4为轮轨接触点的轨道不平顺向量。

(8)将步骤(7)得到的轮轨力作为激励力，施加到步骤(2)中的车辆运动方程中及步骤(3)中的轨-桥耦合模型运动方程中进一步求得车辆、轨道结构及桥梁结构的频域位移响应Z(ω)。

(9)根据速度及加速度与位移之间的关系式，进一步求得车辆、轨道结构及桥梁结构的速度及加速度频域响应。

其中，i为虚数单位，ω为圆频率，Z(ω)、和分别表示频率位移响应、频率速度响应和频率加速度响应。

与现有技术相比，本发明的有益效果是，从车-轨-桥耦合系统振动产生的机理出发，先求解动态轮轨力频谱，再以动态轮轨力作为激励求解车辆、轨道、桥梁结构的频域动力响应；研究关注的频段范围为20～500Hz，属于中高频段，输出的系统响应可用于进一步研究高架轨道交通环境振动和噪声问题，与现有常规的车-轨-桥耦合振动时域模型相比，一是更加准确地考虑了动态轮轨力的中高频激励影响；二是避开时域方法所须采用的分步积分，计算效率大大提高，同时频域结果保证了满足工程要求的计算精度；三是该预测模型适用性强，能应用与不同的车辆类型、轨道结构类型、桥梁结构类型。此外，由于该模型计算输出的响应可作为高架轨道交通环境振动和噪声问题的激励源，通过对该模型的参数研究，从而指导轨道形式选择及桥梁结构设计，对高架轨道交通环境振动及噪声控制具有重要理论意义。

以上内容是结合具体的优选实施方式对本发明所作的进一步详细说明，不能认定本发明的具体实施只局限于这些说明。对于本发明所属技术领域的普通技术人员来说，在不脱离本发明构思的前提下，还可以做出若干简单推演或替换，都应当视为属于本发明的保护范围。