基于蚁群算法的火力分配方法与流程

本发明属于战斗机火力控制技术领域，特指一种基于蚁群算法的火力分配方法。

背景技术：

空战中的火力分配(Weapon-target Assignment,WTA)是指，在综合考虑执行的战斗任务、空战态势以及敌我双方战斗机与导弹性能等因素的基础上，将我方一定数目的某种型号导弹分配给敌方每一架战机的过程。空战态势瞬息万变，需要快速得到优化的火力分配方案。然而，火力分配是一个动态的多变量、多约束组合优化问题，具有对抗性、主动性、不确定性等特性，用传统方法难以解决。近年来出现了人工智能(AI)、专家系统(ES)、人工神经网络(ANN)、模糊空战系统、优化理论(图论、多目标决策、遗传算法等)、信息论(如粗糙集)等方法，可用于火力分配求解，但依然存在可行解空间受限、难以找到最优解、收敛过慢等问题难以解决。

蚁群算法是近年来颇受关注的一种新型模拟进化算法，是目前公认可以有效解决组合优化问题的智能算法之一。该算法具有自组织、正反馈等特点，能够将复杂的组合优化问题映射到低层次的蚂蚁的简单行为。因此，利用蚁群算法解决火力分配这种多变量、多约束的组合优化问题，以利用其正反馈的特性来搜索得到最佳的火力分配方案，是一种可行的空战火力分配求解思路。但是经典蚁群算法还存在诸如前期信息素匮乏、容易陷入局部最优、对大空间问题收敛较慢等方面不足，还不能直接应用到空战火力分配中来。

技术实现要素：

为了解决现有技术的不足，本发明的目的在于提出一种基于蚁群算法的火力分配方法。本发明着眼于蚁群算法的更新机制、路径选择机制和信息素区间机制三个方面，结合经典蚁群系统(Ant Colony System，ACS)与最大-最小蚁群系统(MAX-MIN Ant System，MMAS)算法的思想，对蚁群算法进行改进，使得改进蚁群算法的前期进化趋势更加合理、收敛速度更快并且能够更好地避免陷入局部最优。而且本发明面向火力分配提出的改进蚁群算法不仅可用于空战火力分配，还可望用于其他组合优化问题，如地面坦克群的进攻作战、海上战舰编队作战中的火力分配等决策问题。

本发明首先根据敌我双方交战态势建立空战威胁度模型和火力分配决策模型；其次在模型求解方面，针对经典蚁群算法的不足进行算法改进，设计适合解决空战火力分配的优化算法。

一种基于蚁群算法的火力分配方法，包括以下步骤：

第一步，建立空战火力分配模型，包括空战威胁度模型和火力分配决策模型。

首先评估蓝方战机对红方威胁度，基于此，以预期对蓝方战机打击效果最大化和红方所受威胁最小化为目标，进行火力分配。

设红方N架战机与蓝方K架战机进行空战对抗，其中红方战机与蓝方战机速度、导弹攻击范围、雷达探测范围、机动能力等性能不同，且红方的预警机能够准确识别蓝方战机的型号、速度以及空间位置；设R_i为第i架红方战机，B_j为第j架蓝方战机，为R_i的轴线方向，为R_i的飞行速度，ε_ji为B_j相对于R_i的离轴角，为B_j的轴线方向，为B_j的飞行速度，ε_ij为R_i相对于B_j的离轴角，LOS为双方的视线方向，D_ij为R_i与B_j之间距离。

(1)根据以上空战态势，分别针对角度威胁、距离威胁、速度危险和能力威胁进行建模，然后在此基础上建立蓝方对红方的整体空战威胁度模型。

(1.1)角度威胁函数：

式中S_ij¹表示B_j对R_i的角度威胁度，与R_i和B_j的离轴角之差成正比；其中0°＜ε_ij,ε_ji≤180°，-1≤S_ij¹≤1；当R_i离轴角为180°，B_j离轴角为0°，即B_j在正后方追击R_i时，B_j对R_i的角度威胁度为1。

(1.2)距离威胁函数：

式中表示蓝方导弹的攻击距离，表示蓝方雷达的最大探测距离；

当红方战机位于蓝方攻击范围时，距离威胁度值取最大值1；当红方战机处于蓝方雷达探测距离以外时，距离威胁度取最小值0。

(1.3)速度威胁函数：

式中表示红方战机速度，表示蓝方战机速度。当红方较蓝方的速度越大，则B_j对R_i的速度威胁度越小。

(1.4)能力威胁函数:

首先通过文献得到空战能力公式为：

C＝[ln B+ln(∑A₁+1)+ln(∑A₂)]ε₁ε₂ε₃ε₄ (4)

式中B为战机的机动性能参数；A₁是火力攻击能力参数；A₂为其雷达探测能力衡量参数；ε₁是飞行员的操控能力系数；ε₂是战机生存能力系数；ε₃是战机航程范围系数；ε₄是战机电子对抗能力系数。C的值可以根据飞机型号查表得出。

为便于数据分析，通过各种典型战机能力指数的比较，定义能力威胁函数为：

其中，C_i表示红方战机的空战能力，C_j表示蓝方战机的空战能力。

例如假设红方某型号战机的空战能力为17.9，蓝方战机空战能力为15.8、18.8、17.9、13.6，可以得到蓝方各战机对红方该战机的能力威胁度大小分别为：0.25、0.75、0.5、0.25。

(1.5)结合以上威胁函数的设定可得蓝方战机B_j对红方战机R_i的空战威胁度为：

S_ij＝ω₁S_ij¹+ω₂S_ij²+ω₃S_ij³+ω₄S_ij⁴ (6)

其中0＜ω_i＜1为权重，且∑ω_i＝1。

蓝方战机B_j对整个红方编队的威胁度为：

公式(7)得到的整体威胁度将用来确定对该敌机(即蓝方战机)具体分配的导弹数量。

(2)火力分配决策模型

空战中红方将对蓝方发射一定数量的导弹，火力分配决策模型的目标即为所有导弹化解蓝方的威胁度之和达到最大。

设R_i携带的导弹数量为M_i，对B_j分配的导弹数量为：

其中S_j为蓝方战机B_j对整个红方编队的威胁度。

火力分配决策模型为：

s.t

其中Ω表示所有攻击方案构成的解空间；X_ij表示红方战机携带的第i枚导弹是否用于攻击蓝方战机j，X_ij取值为0或1，1时表示红方战机携带的第i枚导弹用于攻击蓝方战机j，否则为0；k为实际用于攻击目标的导弹数量。

第一个约束条件表示红方每架战机导弹发射数量不超过其载弹量；第二个约束条件表示蓝方每架战机最多被分配公式(8)中求出的导弹数量；第三个约束条件表示任一架蓝方战机都可以被攻击多次，但一枚导弹仅可以攻击一架蓝方战机；第四个约束条件表示，红方发射的导弹总数等于红方带弹总数与蓝方总共需被分配导弹数两者的较小值。

第二步，基于改进的蚁群算法解决空战火力分配的优化问题

将空战火力分配过程模拟成一个蚁群网络。将红方战机的每一发导弹都看作是一个红方的节点，将蓝方每架战机需要分配的导弹看作是一个蓝方的节点。

(2.1)设置种群中蚂蚁数量为：

m＝N_r+ΣE_j (10)

其中N_r为红方携带的导弹总数，E_j为第j架蓝方战机上分配的导弹数量。

(2.2)将m只蚂蚁随机地放置在红方战机的导弹上，并设置各路径上初始信息素浓度均为1。

(2.3)m只蚂蚁按照伪随机概率选择规则选择蓝方应当分配导弹的位置，蚂蚁在移动过程中的规则如下：

规则一：蚂蚁只能够移动到蓝方战机导弹分配数量不足的位置，蓝方每架战机分配的导弹数量不能超过设定的分配数量，红方战机最多发射携带导弹的剩余数。

规则二：红方战机上的每只蚂蚁每次只能到达一个目标点，即每枚导弹只能攻击一个目标。

规则三：每只蚂蚁各自进行目标选择，互不干扰。每只蚂蚁在到达当前允许分配的一个目标后，同样以伪随机概率选择规则返回红方战机位置，此时蚂蚁的移动目标为红方剩余的导弹位置。接着进行下一枚导弹的目标选择，直到完成N_r枚导弹的目标分配。

进一步地，蚂蚁进行目标选择时按照如下伪随机概率选择规则进行：

其中j′为下一个需要访问的节点；J为q＞q₀时，下一个待访问节点，访问J节点的概率p_ij由如下状态转移概率来进行选择(在算法实现中用轮盘赌法的思想依据选择概率p_ij对目标进行选择)：

式中：

J_k(i)为第k只蚂蚁在已访问节点i后仍需要访问的节点集合；

τ(i,s)为当前导弹i与分配位置s之间的信息素浓度；

η(i,s)为启发函数，取为蓝方目标对红方的威胁度，某架蓝方战机对整个红方编队的威胁越大，选择对其进攻的概率越大；

α为信息启发因子，用来衡量路径上信息素的影响程度，取α＝3；

β为期望启发因子，用来衡量蓝方对红方威胁度的影响程度，取β＝0.3；

q₀为初始设定的参数，通过做实验对比分析，取q₀＝0.3；

allowed_k＝{1,2,…,n}-tabu，代表蚂蚁k接下来可以选择的目标点。

在进行目标选择时，存在红方载弹量有限，对蓝方分配导弹数目一定的约束，因此蚂蚁k在从i到j的目标选择时需要检查红方战机i的导弹是否有剩余，蓝方战机j是否还需要分配导弹。

规则四：所有蚂蚁在结束一次循环之后，需要进行信息素的更新，并且每只蚂蚁在各自循环中的最优路径上产生新的信息素，每只蚂蚁产生新的信息素的同时考虑路径上信息素的耗散或挥发。

具体信息素更新方式如下：

τ(i,j)＝(1-ρ₁)·τ(i,j)+ρ₁·Δτ(i,j) (13)

式中：

Δτ(i,j)为最优路径(i，j)上的信息素增量；

S_ij为最优路径上蓝方对红方的威胁度；

ρ₁为信息素在每次循环过程中的挥发系数，通过实验对比分析取ρ₁＝0.6；

ρ₂为比例系数，取ρ₂＝0.2。

设置每条路径的信息素浓度的上限为τ_max(t)，下限为τ_min(t)。更新每条路径信息素的上下限的准则是：若该路径上信息素高于τ_max(t)，则该路径信息素取为τ_max(t)；若该路径上信息素低于τ_min(t)，则取为τ_min(t)。

本发明采用基于改进蚁群算法的火力分配决策方法，相比以往技术方法，具有以下明显优点：

(1)相比经典蚁群算法，本发明改变了路径选择规则、信息素更新规则，并且在每条路径上增加了的信息素浓度区间限定规则，使改进后的蚁群算法能够更好地发挥正反馈机制，从而收敛更快，且易于避免搜索陷入局部最优。

(2)相比其他算法实现，例如粒子群算法、遗传算法等，通过对比发现：本发明较粒子群算法更适合解决此类复杂离散问题，避免出现过早收敛的现象；本发明不存在遗传算法的“基因漂变”现象，能够通过改进避免陷入局部最优。

附图说明

图1本发明实施例中的空战态势示意图。

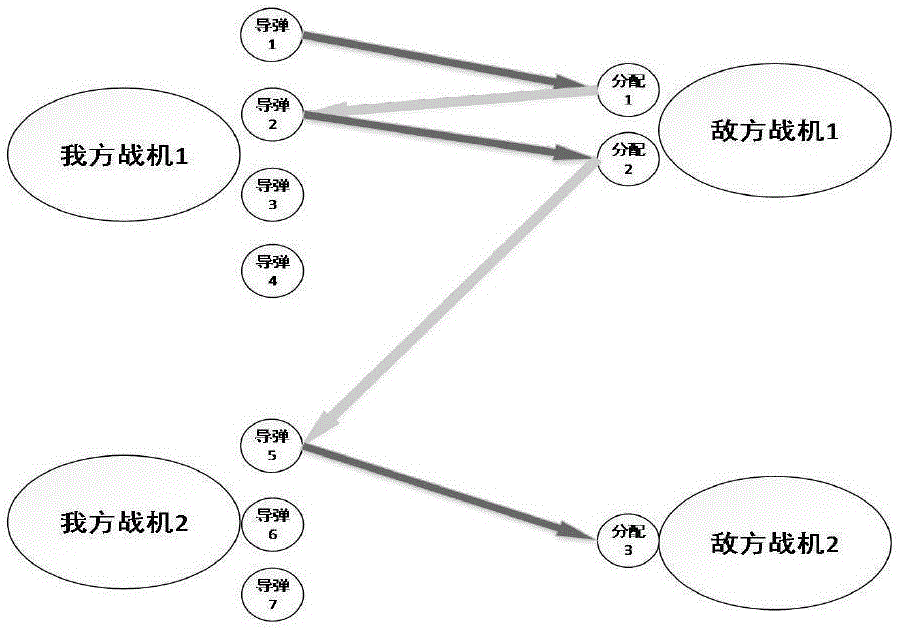
图2本发明实施例中的空战网络示意图。

图3为本发明基于改进蚁群算法求解空战火力分配的伪代码

图4本发明实施例中的实现流程图。

具体实施方式

为使本发明的目的、技术方案和优点更加清楚，下面将结合附图对本发明实施方式作进一步地详细描述。

一种基于蚁群算法的火力分配方法，包括以下步骤：

第一步，建立空战火力分配模型，包括空战威胁度模型和火力分配决策模型。

首先评估蓝方战机对红方威胁度，基于此，以预期对蓝机打击效果最大化和红方所受威胁最小化为目标，进行火力分配。

设红方N架战机与蓝方K架战机进行空战对抗，其中红方战机与蓝方战机战机速度、导弹攻击范围、雷达探测范围、机动能力等性能不同，且红方预警机能够准确识别蓝方战机的型号、速度以及空间位置等基本信息。如图1为用于威胁度建模的空战态势示意图，图1中设R_i为第i架红方战机，B_j为第j架蓝方战机，为R_i的轴线方向，为R_i的飞行速度，ε_ji为B_j相对于R_i的离轴角，为B_j的轴线方向，为B_j的飞行速度，ε_ij为R_i相对于B_j的离轴角，LOS为双方的视线方向，D_ij为R_i与B_j之间距离。

(1)根据以上空战态势，分别针对角度威胁、距离威胁、速度危险和能力威胁进行建模，然后在此基础上建立蓝方对红方的整体空战威胁度模型。

(1.1)角度威胁函数：

式中S_ij¹表示B_j对R_i的角度威胁度，与R_i和B_j的离轴角之差成正比；其中0°＜ε_ij,ε_ji≤180°，-1≤S_ij¹≤1；当R_i离轴角为180°，B_j离轴角为0°，即B_j在正后方追击R_i时，B_j对R_i的角度威胁度为1。

(1.2)距离威胁函数：

式中表示蓝方导弹的攻击距离，表示蓝方雷达的最大探测距离；

当红方战机位于蓝方攻击范围时，距离威胁度值取最大值1；当红方战机处于蓝方雷达探测距离以外时，距离威胁度取最小值0。

(1.3)速度威胁函数：

式中表示红方战机速度，表示蓝方战机速度。当红方较蓝方的速度越大，则B_j对R_i的速度威胁度越小。

(1.4)能力威胁函数:

首先通过文献得到空战能力公式为：

C＝[ln B+ln(∑A₁+1)+ln(∑A₂)]ε₁ε₂ε₃ε₄ (18)

式中B为战机的机动性能参数；A₁是火力攻击能力参数；A₂为其雷达探测能力衡量参数；ε₁是飞行员的操控能力系数；ε₂是战机生存能力系数；ε₃是战机航程范围系数；ε₄是战机电子对抗能力系数。C的值可以根据飞机型号查表得出。

为便于数据分析，通过各种典型战机能力指数的比较，定义能力威胁函数为：

其中，C_i表示红方战机的空战能力，C_j表示蓝方战机的空战能力。

例如假设红方某型号战机的空战能力为17.9，蓝方战机空战能力为15.8、18.8、17.9、13.6，可以得到蓝方各战机对红方该战机的能力威胁度大小分别为：0.25、0.75、0.5、0.25。

(1.5)结合以上威胁函数的设定可得蓝方战机B_j对红方战机R_i的空战威胁度为：

S_ij＝ω₁S_ij¹+ω₂S_ij²+ω₃S_ij³+ω₄S_ij⁴ (20)

其中0＜ω_i＜1为权重，且∑ω_i＝1。

蓝方战机B_j对整个红方编队的威胁度为：

公式(21)得到的整体威胁度将用来确定对该敌机具体分配的导弹数量。

(3)火力分配决策模型

空战中红方将对蓝方发射一定数量的导弹，火力分配决策模型的目标即为所有导弹化解蓝方的威胁度之和达到最大。

设R_i携带的导弹数量为M_i，对B_j分配的导弹数量为：

其中S_j为B_j对红方编队的整体威胁度。

火力分配决策模型为：

s.t

其中Ω表示所有攻击方案构成的解空间；X_ij表示红方战机携带的第i枚导弹是否用于攻击蓝方战机j，X_ij取值为0或1，1时表示红方战机携带的第i枚导弹用于攻击蓝方战机j，否则为0；k为实际用于攻击目标的导弹数量。

第一个约束条件表示红方每架战机导弹发射数量不超过其载弹量；第二个约束条件表示蓝方每架战机最多被分配公式(22)中求出的导弹数量；第三个约束条件表示任一架蓝方战机都可以被攻击多次，但一枚导弹仅可以攻击一架蓝方战机；第四个约束条件表示，红方发射的导弹总数等于红方带弹总数与蓝方总共需被分配导弹数两者的较小值。

下面介绍本发明提供的一种空战火力分配的蚁群算法规则，即一种改进的蚁群算法。

蚁群算法引入了正反馈并行机制，具有较强的自适应性、鲁棒性、优良的分布式计算机制、易于与其他算法结合等全新的特性，在求解TSP问题、job-shop调度问题、分配问题时得到了很好的结果。为解决空战中的火力分配问题，本发明在基本蚁群算法的基础上作如下改进。

(1)路径选择规则

为避免搜索的停滞，路径选择时采用确定性选择和随机性选择相结合，并且在搜索过程中动态调整状态转移概率。具体的路径选择规则如下式：

其中j′为下一个需要访问的节点；J为q＞q₀时，下一个待访问节点，访问J节点的概率p_ij由如下状态转移概率来进行选择(在算法实现中用轮盘赌法的思想依据选择概率p_ij对目标进行选择)：

式中：

J_k(i)为第k只蚂蚁在已访问节点i后仍需要访问的节点集合；

τ(i,s)为当前导弹i与分配位置s之间的信息素浓度；

η(i,s)为启发函数，取为蓝方目标对红方的威胁度，某架蓝方机对红方机群威胁越大，选择对其进攻的概率越大；

α为信息启发因子，用来衡量路径上信息素的影响程度，取α＝3；

β为期望启发因子，用来衡量蓝方对红方威胁度的影响程度，取β＝0.3；

q₀为初始设定的参数，通过做实验对比分析，取q₀＝0.3；

allowed_k＝{1,2,…,n}-tabu，代表蚂蚁k接下来可以选择的目标点。

q为[0,1]之间的一个按均匀分布产生的随机数；q₀为设定的参数(1≤q₀≤1)。当随机数q小于等于q₀时，将选择当前信息素浓度最高的路径作为下一移动节点；当随机数q小大于q₀时，按照路径选择概率公式得到各节点的转移概率，按照概率的大小进行选择移动(算法中用轮盘赌法思想实现)。

上述路径选择机制为自适应伪随机概率选择规则，具体的路径选择实际上由随机数q大小确定。

(2)最优路径信息素更新规则

在进行信息素更新时，仅对当前循环中的最优路径进行信息素更新，强化正反馈的作用。更新规则如下：

τ(i,j)＝(1-ρ₁)·τ(i,j)+ρ₁·Δτ(i,j) (26)

式中，L_gb为当前循环中得到的最短路径长度；ρ₁为(0,1)之间的参数，其意义相当于基本模型中出现过的信息素挥发系数；ρ₂为常数。

(3)信息素浓度区间限定规则

为了避免搜索过程中出现局部停滞现象，在第t次迭代中，在每条路径上设置信息素区间[τ_min(t),τ_max(t)]。由于每次迭代过程中，路径上增加的信息素最大值为ρ₂·L_gb，因此每次迭代都需要更新路径的信息素浓度区间，同时τ_max(t)与信息素挥发率(1-ρ)成反比。第t次迭代过程中的区间公式如下：

在迭代过程中，路径上的信息素浓度一旦大于τ_max(t)就强制取为τ_max(t)，一旦小于τ_min(t)就取为τ_min(t)。

第二步，基于上述改进的蚁群算法解决空战火力分配的优化问题。

将空战火力分配过程模拟成一个蚁群网络。将红方战机的每一发导弹都看作是一个红方的节点，将蓝方每架战机需要分配的导弹看作是一个蓝方的节点，如图2所示。

图2中蓝红双方分别派出两架战机进行作战，红方战机1携带超视距导弹4枚，红方战机2携带3枚。假设根据威胁度模型得到，对蓝方战机1应当分配2枚导弹，对蓝方战机2分配1枚导弹。由此建立空战网络：蚂蚁从红方导弹上出发到达蓝方战机需要分配导弹位置，再根据同样的策略虚拟一条路径回到红方导弹上，直到红方导弹用完或者对蓝方分配完成。图2所示分配方案为：红方战机1发射2枚导弹攻击蓝方战机1，红方战机2发射1枚导弹攻击蓝方战机2。计算所有导弹化解的蓝方威胁度进行求和，得到该方案化解蓝方总威胁度的值，找出所有方案中化解蓝方威胁度最大的方案，即为最优火力分配方案。

不失一般性，基于上述改进的蚁群算法解决空战火力分配的优化问题的实现步骤如下：

(2.1)设置种群中蚂蚁数量为：

m＝N_r+∑E_j (30)

其中N_r为红方携带的导弹总数，E_j为第j架蓝方战机上分配的导弹数量。

(2.2)将m只蚂蚁随机地放置在红方战机的导弹上，并设置各路径上初始信息素浓度均为1。

(2.3)m只蚂蚁按照伪随机概率选择规则选择蓝方应当分配导弹的位置，蚂蚁在移动过程中的规则如下：

规则一：蚂蚁只能够移动到蓝方战机导弹分配数量不足的位置，蓝方每架战机分配的导弹数量不能超过设定的分配数量，红方战机最多发射携带导弹的剩余数。

规则二：红方战机上的每只蚂蚁每次只能到达一个目标点，即每枚导弹只能攻击一个目标。

规则三：每只蚂蚁各自进行目标选择，互不干扰。每只蚂蚁在到达当前允许分配的一个目标后，同样以伪随机概率选择规则返回红方战机位置，此时蚂蚁的移动目标为红方剩余的导弹位置。接着进行下一枚导弹的目标选择，直到完成N_r枚导弹的目标分配。

进一步地，蚂蚁进行目标选择时按照如下伪随机概率选择规则进行：

其中j′为下一个需要访问的节点；J为q＞q₀时，下一个待访问节点，访问J节点的概率p_ij由如下状态转移概率来进行选择(在算法实现中用轮盘赌法的思想依据选择概率p_ij对目标进行选择)：

式中：

J_k(i)为第k只蚂蚁在已访问节点i后仍需要访问的节点集合；

τ(i,s)为当前导弹i与分配位置s之间的信息素浓度；

η(i,s)为启发函数，取为蓝方目标对红方的威胁度，某架蓝方机对红方机群威胁越大，选择对其进攻的概率越大；

α为信息启发因子，用来衡量路径上信息素的影响程度，取α＝3；

β为期望启发因子，用来衡量蓝方对红方威胁度的影响程度，取β＝0.3；

q₀为初始设定的参数，通过做实验对比分析，取q₀＝0.3；

allowed_k＝{1,2,…,n}-tabu，代表蚂蚁k接下来可以选择的目标点。

在进行目标选择时，存在红方载弹量有限，对蓝方分配导弹数目一定的约束，因此蚂蚁k在从i到j的目标选择时需要检查红方战机i的导弹是否有剩余，蓝方战机j是否还需要分配导弹。

规则四：所有蚂蚁在结束一次循环之后，需要进行信息素的更新，并且每只蚂蚁在各自循环中的最优路径上产生新的信息素，每只蚂蚁产生新的信息素的同时考虑路径上信息素的耗散或挥发。

具体信息素更新方式如下：

τ(i,j)＝(1-ρ₁)·τ(i,j)+ρ₁·Δτ(i,j) (33)

式中：

Δτ(i,j)为最优路径(i，j)上的信息素增量；

S_ij为最优路径上蓝方对红方的威胁度；

ρ₁为信息素在每次循环过程中的挥发系数，通过实验对比分析取ρ₁＝0.6；

ρ₂为比例系数，取ρ₂＝0.2。

设置每条路径的信息素浓度的上限为τ_max(t)，下限为τ_min(t)。更新每条路径信息素的上下限的准则是：若该路径上信息素高于τ_max(t)，则该路径信息素取为τ_max(t)；若该路径上信息素低于τ_min(t)，则取为τ_min(t)。通过这种方式对路径上信息素浓度区间进行设定，能有效避免局部路径信息素浓度过高而导致搜索陷入局部最优。

参照图3给出了本发明基于改进蚁群算法求解空战火力分配的伪代码。参照图4示出了本发明基于改进蚁群算法的火力分配方法的流程图，包括以下步骤：

第一步：获取红蓝双方有关数据，调用空战火力分配数学模型，计算相关威胁度。

第二步：参数初始化。

第三步：将m只蚂蚁平均放置在红方战机上。

第四步：各蚂蚁所代表的分配方案中对当前蓝机弹药携带数量减1。

第五步：分布在红方导弹上的蚂蚁根据伪随机概率选择规则进行可行解搜索，蚂蚁移动至相应蓝机位置，对应蓝机所需分配导弹数量减1。以策略返回红方剩余导弹位置。

第六步：计算第k只蚂蚁化解蓝方的威胁度，得到最佳方案，更新最优路径信息素浓度。

第七步：更新信息素浓度区间。

第八步：转到第三步，直到循环终止条件NC>NC_max。

第九步：输出最佳分配方案。

以上包含了本发明优选实施例的说明，这是为了详细说明本发明的技术特征，并不是想要将发明内容限制在实施例所描述的具体形式中，依据本发明内容主旨进行的其他修改和变型也受本专利保护。本发明内容的主旨是由权利要求书所界定，而非由实施例的具体描述所界定。