一种光学相干层析成像系统中相位解缠的方法与流程

本发明属于光电成像技术领域，尤其涉及一种光学相干层析成像系统中相位解缠的方法。

背景技术：

精确的相位信息提供的有价值的信息可用于在物体探测和成像方面。到目前为止，相位图像被广泛用在干涉孔径雷达，核磁共振成像，条纹投影轮廓术，数字全息，显微成像以及光学相干层析等领域。光学相干层析因为分辨率高，可实时三维成像而被广泛应用在生物医学成像中。然而，对于各种血管成像的流体研究，相位图由于测量长度超过一个波长而出现缠绕现象，因此解决相位的不连续性是必要的问题。

为了解决相位缠绕问题，人们在过去已经提出各种方法，这些方法大致可分为：路径跟踪法，最小范数法，网络流法，多波长法以及其他方法。就光学相干层析成像系统中，目前只有一个方法被报道，该方法属于第四种方法，具体来说就是通过合成一个较长的波长来避免这种缠绕现象出现，但是该方法的应用对象是细胞表面成像，所处理的数据仅仅是在x-y平面的信息，没有包含所有深度z方向的信息，故而该方法的通行性较差。

为了重新解决这个问题，我们在由学者Costantini提出网络法的基础上提出了一种鲁棒性较好的相位解缠方法。Costantini提出的网络流法假设真实相位的梯度图像与经过缠绕算子作用在缠绕相位的梯度后的图像之间的误差值是2π的整数倍(这里的梯度图像是指经过x和y方向求导后的图像)，然而对于实际系统的相位图，带有噪声的像素点已经偏离原有的数值，所以带有整数倍的约束关系是不适用于实验中的相位图。因此，基于该假设的不合理性，本文提出了一种适用范围更广的网络流法。

技术实现要素：

为解决相位图像的不连续问题，本发明提供一种光学相干层析成像系统中相位解缠的方法。由于缠绕相位梯度图与真实相位梯度图的差别在于相位跳跃边界的梯度值不一样，将缠绕相位梯度图进行再次缠绕，可得到与真实相位梯度图等价的恢复相位梯度图。

一种光学相干层析成像系统中相位解缠的方法，其基本步骤包括：

步骤一：对输入的缠绕相位图在图像平面坐标系下的x与y方向分别进行求导，得到缠绕相位图x和y方向的缠绕相位梯度图；

步骤二：缠绕相位梯度图经缠绕算子解缠作用后得到恢复相位梯度图，则真实相位梯度图与恢复相位梯度图各个像素点之间的误差表示如下：

其中，(i,j)代表像素点的位置，e₁(i,j)、e₂(i,j)分别为恢复相位梯度图与真实相位梯度图在x和y方向的各个像素点误差；Δφ₁(i,j)、Δφ₂(i,j)分别为x和y方向的真实相位梯度图各个像素点梯度值；分别为x和y方向的缠绕相位梯度图各个像素点梯度值；W为缠绕算子，也即对缠绕相位梯度图进行2π取模操作；

步骤三：将恢复相位梯度图与真实相位梯度图的相邻四个像素点的误差表示为：

e₁(i,j+1)-e₁(i,j)-e₂(i+1,j)+e₂(i,j)＝R(i,j) (2)

其中右边R(i,j)为：

步骤四：以方程(2)为约束条件，通过求解方程(3)的最小值，计算误差e₁(i,j)与e₂(i,j)的值；

其中e₁(i,j)∈R、e₂(i,j)∈R，其中R为实数，且c₁(i,j)、c₂(i,j)为依据Costantini学者提出网络流法中的设置权重；然而在实际系统的相位图中，e₁(i,j)、e₂(i,j)是由于噪声引起的，带有噪声的像素点已经偏离原有的数值，具有不确定性，将其假设为2π的整数倍是不合理的；因此在本发明中，e₁(i,j)、e₂(i,j)可以取任何数值，没有任何约束条件；

步骤五：将步骤四的e₁(i,j)与e₂(i,j)的值代入方程(1)，得到解缠后的真实相位梯度图各个像素点梯度值Δφ₁(i,j)和Δφ₂(i,j)；

步骤六：对真实相位梯度图各个像素点梯度值Δφ₁(i,j)与Δφ₂(i,j)进行路径积分，得到估计真实相位图。

步骤七：计算估计真实相位图在非缠绕区域曲线与缠绕相位图缠绕曲线之间的常数偏移量，取该常数偏移量的中值，对路径积分后的估计真实相位图进行常数纠正，最终得到恢复偏移的真实相位图，解决相位不连续性的问题。

有益效果：

(1)本发明利用缠绕算子对缠绕相位梯度图进行处理，并假设真实相位梯度图与恢复相位梯度图之间的误差可以取任意数值，没有约束条件，很好的解决光学相干成像系统中相位缠绕问题，得到的解缠图与真实图像较为接近，表现出相位的连续性，无缠绕的效果。同时本发明方法还获得了较低的时间成本。

(2)本发明提出的误差项可以取任意值的合理假设，使其能对任一像素点进行处理，也即能补偿由噪声带来的误差。本发明方法无论在哪组噪声水平，都获得了最小的噪声放大系数，有很强的抗噪声能力和较强的鲁棒性，且在解缠过程中具有削弱噪声的能力。

附图说明

图1(a)为本发明光学相干层析成像系统中的透明细管的相位图像；图1(b)为本发明相位图中第110行的相位数值的曲线图；

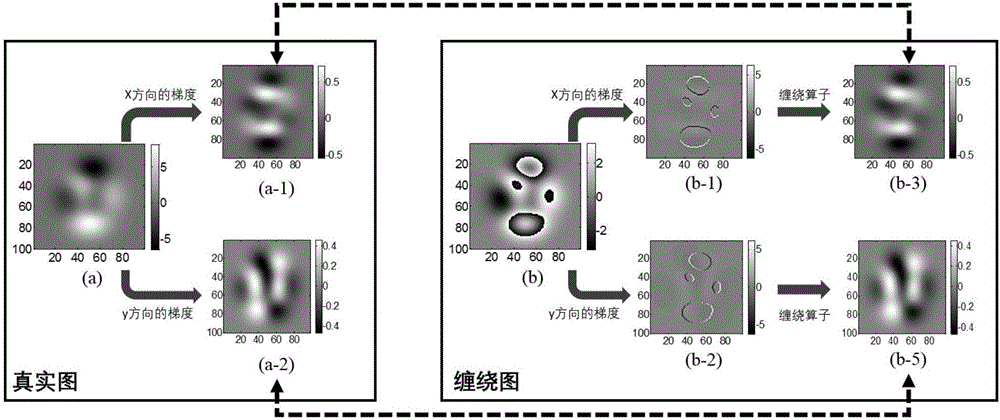
图2为本发明真实图的梯度与缠绕图的梯度之间关系图；图2(a)为真实的相位图；图2(a-1)为真实相位图在x方向上梯度图像；图2(a-2)为真实相位图在y方向上梯度图像；图2(b)为缠绕相位图；图2(b-1)为缠绕图在x方向上梯度图像；图2(b-2)为缠绕图在y方向上梯度图像；图2(b-3)为图2(b-1)经过缠绕算子作用后的图像；图2(b-4)为图2(b-2)经过缠绕算子作用后的图像；

图3为本发明路径积分过程中恢复相位的过程；

图4为本发明提出的解缠方法与常用解缠方法在不同随机脉冲噪声水平下的解缠效果的对比；图4(a)模拟的真实相位图；图4(b)加入不同噪声水平的真实相位图；图4(c)缠绕算子作用在图4(b)后的缠绕相位图；图4(d)最小二乘法的解缠图像；图4(e)路径独立方法的解缠图像；图4(f)网络流法的解缠图像；图4(g)本发明提出的方法的解缠图像。

图5为本发明的不同方法对不同随机脉冲噪声水平的缠绕图像处理结果的三个指标的对比图；三个评价指标分别为：均方根误差RMSE1，噪声放大系数NAD，程序运行时间Time；图5(a)均方根误差RMSE1的比较曲线；图5(b)噪声放大系数NAD的比较曲线；图5(a)程序运行时间Time的比较曲线；

图6为本发明提出的解缠方法与常用解缠的方法的对比效果；图6(a)图1中的相位图，即图1(a)；图6(b)路径跟踪的经典方法的解缠图像；图6(c)傅里叶变换的最小二乘法的解缠图像；图6(d)合成波长方法的解缠图像；图6(e)路径独立方法的解缠图像；图6(f)网络流法的解缠图像；图6(g)本发明提出的方法的解缠图像；图6(h)路径跟踪中经典方法的残差图；图6(i)傅里叶变换的最小二乘法的残差图；图6(j)合成波长方法的残差图；图6(k)路径独立方法的残差图；图6(l)网络流方法的残差图；图6(m)本发明所提出方法的残差图。

图7为本发明的从一维角度看不同方法解缠结果的效果图；选择图6(a)中第110行的相位值进行比较。

具体实施方式

下面结合附图对本发明方法的实施方式做详细说明。

由于缠绕相位梯度图与真实相位梯度图的差别在于相位跳跃边界的梯度值不一样，将缠绕相位梯度图进行再次缠绕，可得到与真实相位梯度图等价的恢复相位梯度图。如图2所示，图2(a-1)和图2(a-2)分别是真实相位图2(a)在x和y方向的两个梯度图像。由于真实的相位图是一个连续图像，所以，从视觉角度来看，图2(a-1)和图2(a-2)的数值分布在很小的区间范围之内。对于缠绕图像图2(b)的两个梯度图像图2(b-1)和图2(b-2)，它们在相位跳跃处有很大的梯度值。在对应位置上，这些大梯度数值相对于真实图的梯度多了2π或-2π这样一个数值，因此通过对缠绕图的梯度图进行缠绕算子操作(对其2π取模操作)，可将多出的梯度相位值消去，也即将跳跃处的梯度恢复到真实图的梯度。

一种光学相干层析成像系统中相位解缠的方法，其具体步骤包括：

步骤一、首先，光学相干层析成像系统对透明细管(牛奶液体在其流动)进行成像，得到细管及其中流体的相位图像(图1(a))。图1(b)展现了图1(a)中第110行相位数值的变化曲线，从图中可以看到，相位在210列的位置，相位从-π跳跃到π，然后在600列左右的位置，相位又从π跳跃到-π，因而相位限定在(-π,π]范围之内。另外，从图1(a)可以看出，相位图有很多脉冲噪声，因此恢复相位是一个很有挑战的问题。

步骤二、得到缠绕相位图后，求得该图像在x和y方向的两个梯度图像，然后再使用缠绕算子对两个梯度图进行处理，同时由于实际系统中的缠绕相位图存在噪声，真实相位梯度图与经缠绕算子作用过后的恢复相位梯度图之间的存在误差：

接着计算恢复相位梯度图与真实相位梯度图的相邻四个点的误差，也即

e₁(i,j+1)-e₁(i,j)-e₂(i+1,j)+e₂(i,j)＝R(i,j) (2)

其中右边R(i,j)为：

然后以方程(2)为约束条件求取方程(3)的最小值从而得到每个像素点的误差e₁(i,j)与e₂(i,j)的数值；

其中e₁(i,j)∈R、e₂(i,j)∈R，其中R为实数，且c₁(i,j)、c₂(i,j)为依据Costantini学者提出网络流法中的设置权重；然而在实际系统的相位图中，e₁(i,j)、e₂(i,j)是由于噪声引起的，带有噪声的像素点已经偏离原有的数值，具有不确定性，将其假设为2π的整数倍是不合理的；因此在本发明中，e₁(i,j)、e₂(i,j)可以取任何数值，没有任何约束条件；最后将计算得到的e₁(i,j)与e₂(i,j)的值代入方程(1)，得到真实相位梯度图。

步骤三、得到真实相位梯度图后，可采用路径积分得到恢复相位。但是，对于噪声较大的缠绕图来说，直接将积分后的图像作为恢复相位，会使得恢复相位相对于真实相位有一个常数偏移量。为了说明该问题，这里以一维数据进行描述，如图3所示。图中解缠的曲线在非缠绕区域，相对于缠绕曲线有一个偏移量，而实际情况，两者应该重合才是。当求其两者曲线的差值时，很明显看到在相位非缠绕区域，该偏移量是一个常数值，因此本发明通过取这条差值曲线的中值，即可得到该偏移量。这样对积分后的相位进行一个常数纠正，就可以得到比较合理的恢复偏移的真实相位图。

步骤四、步骤二至三完成了整个解缠过程，为了说明本发明方法的优势，这里选择如下常用的五种解缠方法(路径跟踪中的经典方法，傅里叶变换的最小二乘法，合成波长方法，路径独立的方法，网络流方法)对模拟缠绕图进行测试比较。由于路径跟踪方法需要强度图像，以及合成波长方法需要从实际系统中得到多个相位图，而此步骤中的模拟图无法满足这些要求，所以在模拟实验中只选择三种方法进行比较。

为了定量化的比较各种方法的解缠效果，这里引入三个指标：第一个指标是真实的相位图与恢复的相位图之间的均方根误差

其中φ_i,j为恢复相位在(i,j)位置处的相位值，I_i,j为真实相位在(i,j)位置处的相位值，m和n分别为相位的宽度和高度；第二个指标是噪声放大系数(Noise amplification degree,NAD)

其中L_i,j为带有噪声的真实相位在(i,j)位置处的相位值。该指标比较的是恢复相位与带噪声的真实相位与真实图像的接近程度。因此，一个好解缠方法的NAD值应该是小于或等于1的；第三个指标是程序的运行时间。解缠时间是必须考虑的，因为高成本的时间对于实际系统中的缠绕图来说是无法接受的。

图4显示了不同方法对10％至90％的噪声水平下的缠绕图的解缠结果。从视觉来看，在10％和20％的噪声下，最小二乘法和网络流法得到了较好的解缠结果，但是更高噪声下的解缠结果是极差的。对于路径独立方法，无论是哪组缠绕图像，解缠结果都是极为不合理的，这可能是由于该方法在解缠过程中，降噪技术对相位梯度进行过分的降噪处理，导致相位发生了严重的变形。而从比较结果来看，本发明提出方法得到了最好的解缠图像，并且从图像的视觉来看，该方法竟也能在60％的高噪声水平下得到令人满意的解缠图像。另外，仔细对于网络流方法与本发明的方法，可以看出，在噪声为10％和20％的情况，它们的解缠结果是类似的，而高噪声情况下，网络流的解缠图像出现了很多明显的线条，但是本发明的方法却能很好的避免这个问题，这其中的原因在于开始的假设。由于网络流方法假设误差项是2π的整数陪，但事实上，噪声是不确定的，所以该假设的引入会使得在一些像素点的相位值比实际上的数值多一点或者少一点，这样经过大量的像素点的累计，明显的线条就出现在解缠图像上了。与之相反的，本发明的解缠图上，不仅没有明显的线条，而且可以发现，解缠的图像图4(g)与带有噪声的真实图像图4(b)相比，具有更低的噪声，因此本发明方法的另一个优点就是在解缠过程中，能削弱噪声的强度。事实上，这种削弱噪声的优势也是来自于误差项可以取任意值的合理假设，因为该假设能对任一像素点进行处理，也就是说它能补偿由噪声带有的误差。为了更直观的比较各个方法，图5显示了上述三个指标的曲线。从曲线的趋势来看图5(b)，本发明方法无论在哪组噪声水平，都获得了最小的NAD数值，并且该数值基本保持在0.42附近，可见本发明方法能在一定程度上削弱噪声。从图5(a)来看，在噪声水平低于80％，本发明方法也获得了最小的均方根误差RMSE1，这也反映了本发明方法的解缠图和真实的图像是比较接近的。对于时间的比较曲线图5(c)，尽管本发明方法的时间成本不是最低，但是总的来说，还是可以接受的。

步骤五、为了验证本发明方法对实际缠绕图像的处理的结果，这里选择了光学相干层析系统中的相位图像作为解缠对象。为了对比描述，这里选择了上文提及的五种解缠方法。另外，考虑到实际系统中无法生成真实图像最为参考，因此，这里选择了两个指标来评估各个解缠方法。第一个指标是：缠绕图像与缠绕算子作用在恢复相位图像后的缠绕图的均方根误差

其中E_i,j为当解缠图像接近真实图像时，那么E_i,j也就接近于0，因此一个优秀的解缠方法的RMSE2应该是接近于0的；第二个指标是解缠时间。

图6显示了五种方法的解缠结果的对比。从图6(b)至图6(g)的对比来看，除了本发明的方法，其他方法的解缠结果都是非常糟糕的。另外从图6(h)-图6(m)的残差图中每个像素点的E_i,j值，也可以明显的看到，只有本发明方法的残差图的数值是最接近于0的。图7显示了第110行相位值曲线，从曲线的变化趋势来看，本发明的解缠曲线要更优于其他五种方法。仔细分析本发明解缠曲线，可以看到在非相位缠绕区域，解缠曲线与缠绕曲线基本重合；在缠绕区域，解缠曲线与缠绕曲线的趋势是一致的，总的来说，解缠曲线基本与缠绕曲线维持同步的波动趋势。表1列出六种方法的均方根误差RMSE2和解缠时间。从对比结果来看，本发明提出的方法的均方根误差是最小的。对于解缠时间，本发明的解缠时间虽然不是最短的，但是相对于网络流法是比较短的，因此该方法的解缠时间还是可接受的。

从模拟相位图与光学相干层析中的相位图的测试结果来看，本发明方法均获得了满意的结果。该方法在解缠过程中解决相位不连续性的同时，也能削弱噪声强度，因此该方法具有对噪声较强的鲁棒性和解决相位不连续性问题的特点。

表1本发明提及的五种方法的均方根误差RMSE2和程序运行时间对比

自此，就实现了光学相干层析成像系统中相位解缠。

该方法得到的解缠图像在非缠绕区域，与缠绕图像基本一致；在缠绕区域，与缠绕相位的趋势一致相同。因此该方法能很好的解决光学相干层析成像系统中相位不连续的问题，扩展了相位信息的应用范围。

当然，本发明还可有其他多种实施例，在不背离本发明精神及其实质的情况下，熟悉本领域的技术人员当可根据本发明作出各种相应的改变和变形，但这些相应的改变和变形都应属于本发明所附的权利要求的保护范围。