一种基于遗传蚁群融合算法的数字微流控芯片灾难性故障测试方法与流程
本发明涉及数字微流控芯片测试技术,具体是一种基于遗传蚁群融合算法的数字微流控芯片灾难性故障测试方法。
背景技术:
数字微流控芯片常用于临床检测、医药工程等对可靠性要求高的领域,因此需要对数字微流控芯片进行全面且高效的测试,保证其可靠性。数字微流控芯片的故障可分为灾难性故障和参数性故障,灾难性故障又可细分为绝缘体击穿、相邻电极短路、电极板断路等故障。灾难性故障对芯片的破坏性是致命的,会导致芯片上实验液滴的完全停滞,使芯片无法正常工作。因此,对灾难性故障的测试是数字微流控芯片测试工作中特别重要的一步。
数字微流控芯片的灾难性故障测试原理为:利用测试液滴遍历数字微流控芯片的阵列单元,若无故障,则测试液滴在遍历后能够到达数字微流控芯片上的废液池,若存在故障,则会导致测试液滴在数字微流控芯片上的停滞,测试液滴无法到达数字微流控芯片上的废液池。废液池处有检测液滴是否到达的检测电路,若检测电路检测到测试液滴的到达,则说明数字微流控芯片无故障,否则,说明存在故障。测试液滴遍历数字微流控芯片的阵列单元的不同路由次序就形成了不同的测试路径,测试路径越短则测试花费的时间就越少,测试效率越高。另外,测试算法本身的复杂度越低、收敛性越好,则测试算法的执行效率越高,更有利于算法的在实际工作中的执行。
目前,针对数字微流控芯片的灾难性故障,已有多种测试方法,如汉密尔顿回路测试法、欧拉回路测试法、并行扫描测试法、内建自测试法、分区子阵列合并调度测试法、基于蚁群算法的搜索测试路径的方法等。在这些方法中,汉密尔顿回路测试法、分区子阵列合并调度测试法无法检测出相邻电极短路故障;并行扫描测试法、内建自测试法只适用于规则矩形阵列的数字微流控芯片的测试,且在线测试效率较低;欧拉回路测试法在应用大规模芯片测试时算法复杂度较高且在线测试效率较低;基于蚁群算法的搜索测试路径的方法,测试模型的建立步骤较繁琐,且单一的蚁群算法收敛性较差,在应用大规模芯片测试时效率较低。
技术实现要素:
本发明目的是针对技术中的不足,而提供一种基于遗传蚁群融合算法的数字微流控芯片灾难性故障测试方法。这种测试方法不但能改善单一蚁群算法收敛性差的问题,而且提高测试算法的执行效率,并且能快速求得测试路径,这种测试方法能够检测出相邻电极短路故障,且兼容规则与非规则阵列芯片的测试,更有利于应用于大规模芯片的测试。
实现本发明目的的技术方案是:
一种基于遗传蚁群融合算法的数字微流控芯片灾难性故障测试方法,与现有技术不同的是,包括以下步骤:
S1.建立数字微流控芯片的灾难性故障测试模型:根据数字微流控芯片的阵列单元结构,建立数字微流控芯片的灾难性故障测试模型,所述模型为:
(1)把数字微流控芯片的阵列单元抽象为无向图G(V,E)的顶点V,相邻阵列单元之间的连接关系抽象为无间图G(V,E)的边E,得到无间图模型G(V,E),并建立其对应的邻接矩阵A;
(2)对无向图模型G(V,E)中的所有顶点V进行编号,令每个顶点的编号对应为该顶点在邻接矩阵A中的行号,从编号最小的顶点开始,依次搜索与当前顶点相关联的边,并对搜索到的边从小到大进行编号;
(3)将无向图模型G(V,E)中的边E抽象为无向图模型G′(V′,E′)的顶点V′,并令顶点V′的编号一一对应G(V,E)中边E的编号,将无向图模型G(V,E)中边E之间的邻接关系抽象为无向图模型G′(V′,E′)的边E′,建立无向图模型G′(V′,E′)及其对应的邻接矩阵B;
(4)采用改进的Floyd方法计算无向图模型G′(V′,E′)中任意两顶点间的最短路径,以两顶点间的最短路径作为两顶点间边的权值,构造一个完全连通图模型G″(V″,E″),以此完全连通图模型G″(V″,E″)作为数字微流控芯片灾难性故障测试的模型;
S2.得到初步测试路径并设置最大最小蚁群算法的初始信息素上下界和信息素初始值:根据数字微流控芯片灾难性故障测试模型G″(V″,E″),采用遗传算法得到初步测试路径,并根据初步测试路径设置最大最小蚁群算法的初始信息素上下界和信息素初始值,其中,初始信息素上下界和信息素初始值具体设置公式为:
其中,τmax(0)、τmin(0)分别为初始信息素上界和下界,是遗传算法求得的初步测试路径中最短测试路径的长度,Pbest表示蚁群算法收敛时构造最优解的概率,avg等于m/2,m是最大最小蚁群算法中设置的蚂蚁数量,ρ是信息素残留系数,τij(0)为任意路径(i,j)上的信息素初值,u表示从遗传算法求得初步测试路径中选择最短的u个测试路径,是遗传算法求得的初步测试路径中的一个测试路径k的长度;
S3.搜索最终测试路径并输出结果:根据数字微流控芯片灾难性故障测试模型G″(V″,E″)和步骤S2得到的初始信息素上下界和信息素初始值,采用最大最小蚁群算法搜索最终测试路径,蚁群算法迭代完成后,输出最终测试路径,其中,最大最小蚁群算法的目标函数为:
其中,为最终测试路径中两个相邻路由节点v″i和v″i+1之间的距离权值,路由节点v″i和v″i+1即为数字微流控芯片灾难性故障测试模型G″(V″,E″)中的两个顶点。
所述步骤S1中的改进Floyd方法为:
在计算无向图G′(V′,E′)中任意两顶点v′i和v′j之间最短路径时,先对待插入的节点v′r进行路长比较,如果dir≥dij或drj≥dij,dij代表两个顶点之间的距离,则说明插入节点v′r后,v′i经过v′r到达v′j的路径不会比原来两顶点之间的路径短,于是不再计算dir+drj,直接进行下一节点的搜索,且无向图G′(V′,E′)中顶点v′i到v′j的距离与v′j到v′i的距离对称相等,若已计算v′i到v′j的距离,则不需再计算v′j到v′i的距离,这样做减少了计算量。
所述步骤S2中遗传算法的染色体编码方案采用十进制整数编码,以初步测试路径的一个路由节点次序作为一条染色体,且染色体编码的起始位代表数字微流控芯片上液滴源所在的位置,编码末位代表数字微流控芯片上废液池所在的位置。
所述步骤S2中的遗传算法的选择算子采用适应度比例方法,交叉算子采用顺序交叉法,变异算子采用逆转变异方法,且染色体起始位和末位不参与交叉操作和变异操作。
所述步骤S3中的最大最小蚁群算法在搜索最终测试路径时,按照伪随机比例规则搜索最终测试路径的节点,具体地,蚂蚁按照下面的公式搜索最终测试路径的节点:
其中,q0∈(0,1)是常数,q∈(0,1)是随机数,τij(t)表示t时刻节点v″i和v″j间的信息素,ηij(t)表示启发信息,ηij(t)=1/dij,dij为数字微流控芯片灾难性故障测试模型G″(V″,E″)中两节点v″i和v″j间的距离,α和β分别表示影响信息素和启发信息的相对强弱的两个参数。
所述步骤S3中最大最小蚁群算法的信息素更新策略为:只允许每次迭代后的最短测试路径增加信息素,具体地,信息素按照下面的公式更新:
其中,ρ是信息素残留系数,Δτij(t)表示路径(i,j)上的信息素增量。f(Sbest)为本次最大最小蚁群算法迭代中最短测试路径的长度Lls或当前全局最短测试路径的长度Lgs。
所述步骤S3中的最大最小蚁群算法的信息素上下界采用动态更新策略,具体地,信息素上下界更新公式如下:
其中,τmax(t)、τmin(t)为t时刻信息素的上下界,Lls为本次最大最小蚁群算法迭代后最短测试路径的长度。
所述步骤S3中采用最大最小蚁群算法搜索最终测试路径时,为了防止液滴之间的意外融合,测试液滴需要满足静态约束条件和动态约束条件。
这种测试方法不但改善了单一蚁群算法收敛性差的问题,而且提高了测试算法的执行效率,并且能快速求得测试路径。这种测试方法能够检测出相邻电极短路故障,且兼容规则阵列与非规则阵列数字微流控芯片,更有利于应用于大规模数字微流控芯片的灾难性故障测试。
附图说明
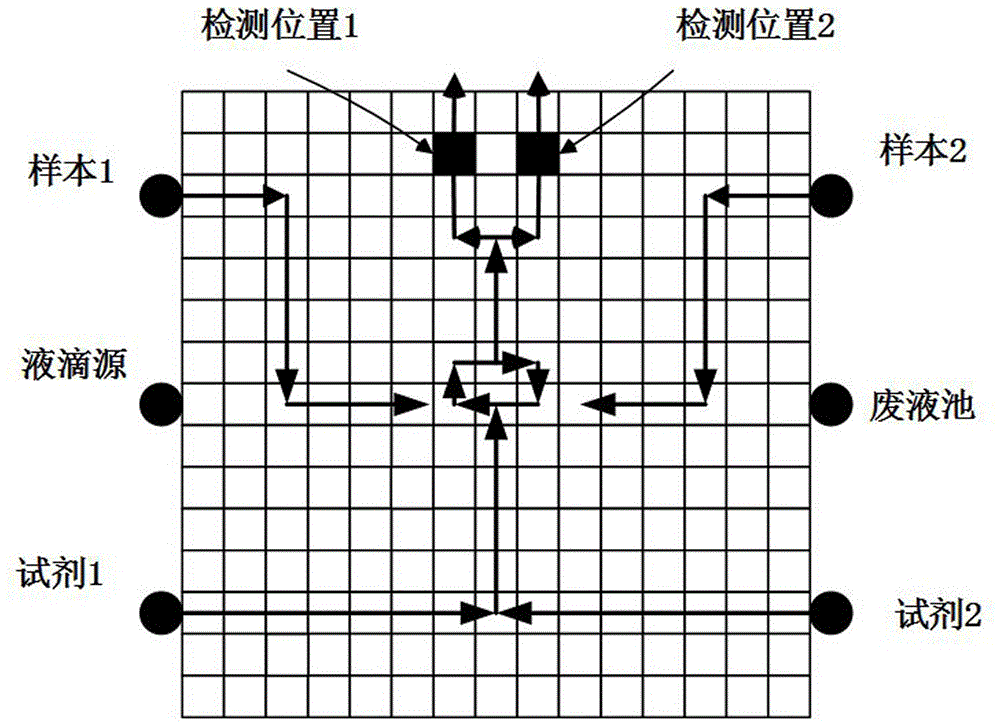
图1为实施例多元生化实验的数字微流控芯片的结构示意图;
图2为一个3×3规则阵列数字微流控芯片的灾难性故障测试模型转换示意图;
图3为数字微流控芯片上液滴之间的约束条件示意图;
图4为实施例方法应用于多元生化实验数字微流控芯片的灾难性故障测试的方法收敛示意图;
图5为实施例方法与欧拉回路法、蚁群测试算法分别应用于多元生化实验数字微流控芯片的灾难性故障测试所花费的测试时间对比示意图;
图6为实施例方法的流程示意图。
具体实施方式
下面结合附图和实施例对本发明内容作进一步的阐述,但并不是对本发明的限定。
实施例:
参照图6,一种基于遗传蚁群融合算法的数字微流控芯片灾难性故障测试方法,包括以下步骤:
S1.建立数字微流控芯片的灾难性故障测试模型:根据数字微流控芯片的阵列单元结构,建立数字微流控芯片的灾难性故障测试模型,所述模型为:
(1)把数字微流控芯片的阵列单元抽象为无向图G(V,E)的顶点V,相邻阵列单元之间的连接关系抽象为无向图G(V,E)的边E,得到无向图模型G(V,E),并建立其对应的邻接矩阵A;
(2)对无向图模型G(V,E)中的所有顶点V进行编号,令每个顶点的编号对应为该顶点在邻接矩阵A中的行号,从编号最小的顶点开始,依次搜索与当前顶点相关联的边,并对搜索到的边从小到大进行编号;
(3)将无向图模型G(V,E)中的边E抽象为无向图模型G′(V′,E′)的顶点V′,并令顶点V′的编号一一对应G(V,E)中边E的编号,将无向图模型G(V,E)中边E之间的邻接关系抽象为无向图模型G′(V′,E′)的边E′,建立无向图模型G′(V′,E′)及其对应的邻接矩阵B;
(4)采用改进的Floyd方法计算无向图模型G′(V′,E′)中任意两顶点间的最短路径,以两顶点间的最短路径作为两顶点间边的权值,构造一个完全连通图模型G″(V″,E″),以此完全连通图模型G″(V″,E″)作为数字微流控芯片灾难性故障测试的模型;
如图1所示的多元生化实验的数字微流控芯片,该数字微流控芯片有一个测试液滴源和一个废液池,图中的箭头方向为实验液滴的移动路径,检测位置1和2是检测实验液滴反应结果的位置,为了对其进行灾难性故障测试,需要测试液滴从液滴源出发遍历整个数字微流控芯片后到达废液池,为了防止液滴之间的意外融合,测试液滴之间需要满足静态约束条件和动态约束条件,该数字微流控芯片阵列单元数为225个,数量较大,因此为了对测试模型转化的过程进行直观的说明,参照图2的3×3规则阵列的数字微流控芯片,具体为:
(1)把3×3规则阵列的数字微流控芯片的阵列单元抽象为无向图模型G(V,E)中的顶点V,阵列单元的相邻关系抽象为边E,得到如图2中所示的无向图模型G(V,E),并建立与无向模型G(V,E)对应的邻接矩阵A;
(2)对图2所示的无向图模型G(V,E)中顶点V进行编号,顶点的编号对应为顶点在邻接矩阵A的行号,从编号最小的顶点开始,依次搜索与当前顶点相关联的边,并对搜索到的边从小到大进行编号,如图2所示无向图模型G(V,E)中边E的编号为“1”到“12”;
(3)将无向图模型G(V,E)中的边E抽象为将无向图模型G′(V′,E′)的顶点V′,将无向图模型G(V,E)中边E之间的邻接关系抽象为无向图模型G′(V′,E′)的边E′,得到无向图模型G′(V′,E′),所述无向图模型G(V,E)中边E之间的邻接关系为:若无向图模型G(V,E)中的两条边有共同顶点,说明这两条边是邻接的,则其对应的无向图模型G′(V′,E′)中的顶点之间存在一条边,如附图2所示将无向图G(V,E)中编号为“11”和“12”的边抽象为无向图G′(V′,E′)的顶点,编号为“11”和“12”的两条边存在共同的顶点,则其抽象为图G′(V′,E′)中的两个顶点之间存在一条边;
(4)最后根据无向图模型G′(V′,E′),利用改进的Floyd方法计算G′(V′,E′)中任意两顶点间的最短路径,以两顶点之间最短路径作为两顶点间边的权值,构造一个完全连通图模型G″(V″,E″),以此完全连通图模型G″(V″,E″)作为数字微流控芯片灾难性故障测试的模型。如图2所示的3×3规则阵列数字微流控芯片转化的完全连通图G″(V″,E″)中有12个顶点,则其对应条边,由于边数太多无法直观画出来,故测试模型转换中没有给出完全连通图G″(V″,E″)的具体图形。
上述步骤S1中数字微流控芯片灾难性故障测试模型的转换方法适用于所有规则和非规则阵列的数字微流控芯片。
S2.得到初步测试路径并设置最大最小蚁群算法的初始信息素上下界和信息素初始值:根据数字微流控芯片灾难性故障测试模型G″(V″,E″)采用遗传算法得到初步测试路径,并根据初步测试路径设置最大最小蚁群算法的初始信息素上下界和信息素初始值,其中,初始信息素上下界和信息素初始值具体设置公式为:
其中,τmax(0)、τmin(0)分别为初始信息素上界和下界,是遗传算法求得的初步测试路径中最短测试路径的长度,Pbest表示蚁群算法收敛时构造最优解的概率,avg等于m/2,m是最大最小蚁群算法中设置的蚂蚁数量,ρ是信息素残留系数,τij(0)为任意路径(i,j)上的信息素初值,u表示从遗传算法求得初步测试路径中选择最短的u个测试路径,是遗传算法求得的初步测试路径中的一个测试路径k的长度;
具体为:
在遗传算法迭代完成后,从遗传算法求得的初步测试路径中,选择其中较短的初步测试路径来计算最大最小蚁群算法的初始信息素上下界和信息素初始值,本实施例应用于多元生化实验数字微流控芯片的灾难性故障测试中,相关参数的优选的方案为:遗传算法的迭代次数设为150次,种群的染色体数量N设为50,迭代完成后在求得的50条初步测试路径中取前u=30条最短的初步测试路径来形成初始信息素上下界和信息素初始值,取ρ=0.92,Pbest=0.05,蚂蚁的数量m=30;
S3.搜索最终测试路径并输出结果:根据数字微流控芯片灾难性故障测试模型G″(V″,E″)和步骤S2得到的初始信息素上下界和信息素初始值,采用最大最小蚁群算法搜索最终测试路径,蚁群算法迭代完成后,输出最终测试路径,其中,最大最小蚁群算法的目标函数为:
其中,为最终测试路径中两个相邻路由节点v″i和v″i+1之间的距离权值,路由节点v″i和v″i+1即为数字微流控芯片灾难性故障测试模型G″(V″,E″)中的两个顶点。
所述步骤S1中的改进Floyd方法为:
在计算无向图G′(V′,E′)中任意两顶点v′i和v′j之间最短路径时,先对待插入的节点v′r进行路长比较,如果dir≥dij或drj≥dij,dij代表两个顶点之间的距离,则说明插入节点v′r后,v′i经过v′r到达v′j的路径不会比原来两顶点之间的路径短,于是不再计算dir+drj,直接进行下一节点的搜索,且无向图G′(V′,E′)中顶点v′i到v′j的距离与v′j到v′i的距离对称相等,若已计算v′i到v′j的距离,则不需再计算v′j到v′i的距离,这样做减少了计算量。
具体的,改进后的Floyd方法的流程如下:
S2-1)从无向图模型G′(V′,E′)中编号最小的顶点开始,搜索任意一对顶点v′i与v′j之间,是否存在另一个顶点v′r,使v′i经过v′r到v′j的距离比当前v′i到v′j的距离短,若是则更新v′i与v′j之间的距离,否则继续搜索下一节点;比较距离时,可以对待插入的节点v′r先进行路长比较,如果dir≥dij或drj≥dij(dij代表两个顶点之间的距离),则说明插入节点v′r后,v′i经过v′r到达v′j的路径不会比原来两点之间的路径短,则直接进行下一节点的搜索;
S2-2)更新任意两顶点之间的距离权值之后,得到一个完全连通图G″(V″,E″)的邻接矩阵C。在算法迭代过程中,由于v′i到v′j的距离与v′j到v′i的距离相等,若已更新v′i到v′j的距离,则不需再计算v′j到v′i的距离,可以提高Floyd方法的效率。
所述步骤S2中遗传算法的染色体编码方案采用十进制整数编码,以测试路径的一个路由节点次序作为一条染色体,且染色体编码的起始位代表数字微流控芯片上液滴源所在的位置,编码末位代表数字微流控芯片上废液池所在的位置,染色体十进制整数编码的方案为:
将测试模型G″(V″,E″)中顶点的十进制编号作为染色体的基因的编码,如附图2中所示的G″(V″,E″)中顶点编号为从“1”到“12”,则可以编码染色体为(1-2-3-4-5-6-7-8-9-10-11-12)或任意其他情况的顶点编号的排列组合。
所述步骤S2中的遗传算法的选择算子采用适应度比例方法,交叉算子采用顺序交叉法,变异算子采用逆转变异方法,且染色体起始位和末位不参与交叉操作和变异操作,交叉操作和变异操作流程如下:
S2-3)利用遗传算法求解测试路径时,每一次迭代需要采用适应度比例方法从种群N中选择M/2(M≥N)对染色体进行交叉操作。具体的,个体k被选择的概率为:
fk=1/Lk
其中,fk为适应度函数,为染色体Xk代表的测试路径中两个相邻节点xi和xi+1之间的距离,N为种群的染色体数量;本实施例中,M的一种优选值为80,N设为50。
S2-4)染色体选择完成后,采用顺序交叉法对选择的M/2对染色体进行交叉操作,且测试路径的起点和终点代表液滴源和废液池,不参与交叉操作。本实施例中,附图1所示数字微流控芯片阵列单元之间连接边的数量为420,数量较大,不便于直观说明交叉的具体操作。不失一般性,以10个基因的染色体为例,来直观地说明顺序交叉法的交叉过程如下:
①随机在父串上选择一个交叉区域,如两父串和交叉区域为:
X1=x0x1x2|x3x4x5x6|x7x8x9
X2=x0x8x4|x7x6x2x1|x3x5x9
②将X2的交叉区加到X1中起点x0后面,同样将X1的交叉区加到X2中起点x0后面,可得:
X′1=x0|x7x6x2x1|x1x2x3x4x5x6x7x8x9
X′2=x0|x3x4x5x6|x8x4x7x6x2x1x3x5x9
③依次删除X′1和X′2中与交叉区相同的基因,得到最终的子串:
X″1=x0x7x6x2x1x3x4x5x8x9
X″2=x0x3x4x5x6x8x7x2x1x9
S2-5)交叉操作完成后,采用逆转变异方法对染色体进行变异操作;同样,以10个基因的染色体为例进行说明:如染色体(x0x1x2x3x4x5x6x7x8x9)在区间x2x3和区间x6x7处发生断裂,断裂片段又以反向顺序插入,于是逆转后的染色体变为(x0x1x2x6x5x4x3x7x8x9)。
S2-6)变异操作完成后,将种群中的个体按适应度从大到小排序,从大到小选择N个适应度高的个体,作为下一次迭代的种群;迭代次数加1,并判断是否达到设置的迭代次数,若达到则终止遗传算法,否则,进入下一次遗传算法的循环,直至迭代完成。
所述步骤S3中的最大最小蚁群算法在搜索最终测试路径时,按照伪随机比例规则搜索最终测试路径的节点,具体地,蚂蚁按照下面的公式搜索最终测试路径的节点:
其中,q0∈(0,1)是常数,q∈(0,1)是随机数,τij(t)表示t时刻节点v″i和v″j间的信息素,ηij(t)表示启发信息,ηij(t)=1/dij,dij为数字微流控芯片灾难性故障测试模型G″(V″,E″)中两节点v″i和v″j间的距离,α和β分别表示影响信息素和启发信息的相对强弱的两个参数。
蚂蚁搜索最终测试路径节点的具体过程如下:
蚂蚁在选择下一节点时,先随机生成q,若q≤q0,则选择使[τil(t)]α[ηil(t)]β值最大的节点j否则按概率公式选择下一个路由节点,按照公式计算每个节点被选择的概率后,按照“轮盘赌”的方式选择下一测试节点,即概率值越高被选择的可能性越大。l∈allowedk表示节点l在可选的集合中,蚂蚁选择此节点后就从allowedk集合中删除此节点,防止测试液滴的重复遍历,提高测试效率。
本例中,最大最小蚁群算法的相关参数的优选设置方案如下:
蚂蚁数量m=30,伪随机比例规则中的q0=0.1,信息素启发系数α=1.2,启发因子系数β=3.0,信息素残留系数ρ=0.92,收敛于最优解的概率Pbest=0.05,蚁群算法迭代次数设为1850。
步骤S3中最大最小蚁群算法的信息素更新策略为:只允许每次迭代后的最短测试路径增加信息素,具体地,信息素按照下面的公式更新:
其中,ρ是信息素残留系数,Δτij(t)表示路径(i,j)上的信息素增量。f(Sbest)为本次最大最小蚁群算法迭代中最短测试路径的长度Lls或当前全局最短测试路径的长度Lgs。
所述f(Sbest)的具体设置方案为:在蚁群算法搜索测试路径时,每次迭代后都采用本次迭代中最短测试路径的长度Lls的值更新信息素,在固定的迭代次数选择使用当前全局最短测试路径的长度Lgs。本实施例中每迭代50次就使用一次前全局最短测试路径的长度Lgs的值。
所述步骤S3中最大最小蚁群算法的信息素更新策略为:只允许每次迭代后的最短测试路径增加信息素,具体地,信息素按照下面的公式更新:
其中,ρ是信息素残留系数,Δτij(t)表示路径(i,j)上的信息素增量。f(Sbest)为本次最大最小蚁群算法迭代中最短测试路径的长度Lls或当前全局最短测试路径的长度Lgs。
所述步骤S3中的最大最小蚁群算法的信息素上下界采用动态更新策略,具体地,信息素上下界更新公式如下:
其中,τmax(t)、τmin(t)为t时刻信息素的上下界,Lls为本次最大最小蚁群算法迭代后最短测试路径的长度。
所述步骤S3中采用最大最小蚁群算法搜索最终测试路径时,为了防止液滴之间的意外融合,测试液滴需要满足静态约束条件和动态约束条件,液滴之间的静态约束条件和动态约束条件说明如下:如图5所示,黑色实心圆表示液滴,“×”表示此单元此时刻t不能被测试液滴访问,静态约束条件是指液滴周围直线相邻和对角相邻的单元上,同一时刻t不能同时存在其他液滴,即为了防止液滴间的意外融合,液滴之间需要保持一定的距离,用公式表示如下:
或
动态约束条件是指液滴下一时刻移动的位置不能与其他液滴相邻,用公式可表示为:
根据实验液滴的移动路径和约束条件可以确定任意时刻t不能被测试液滴访问的单元的集合,记为禁忌表tab(t)。在利用最大最小蚁群算法搜索测试路径中的节点时,若某时刻t选择的路由节点j处于禁忌表tab(t)中,则表示此节点当前不可访问,查询此节点被禁止的时间,设为等待时间twait;按照伪随机比例规则重新搜索新的节点x,将当前节点i到原选择节点j的距离权值加上等待时间twait的权值与当前节点i到新节点x的距离权值作比较,若到达新节点x距离权值较小,则测试液滴向新节点x移动,否则测试液滴在当前节点i等待原选节点j被激活,选择节点j。
步骤S3中采用最大最小蚁群算法搜索最终测试路径时,当蚁群算法迭代次数到达设定值后,输出求得最终测试路径。本实施例中最大最小蚁群算法迭代1850次后,输出求得的最终测试路径,并根据求得的最终测试路径计算测试花费的单位时间,测试路径越长则测试花费的单位时间越多,测试路径越短则测试花费的单位时间越少。测试花费的单位时间越少,说明测试效率越高。其中,单位时间为测试液滴从一个单元移动到相邻单元花费的时间,本实施例中,如图1所示的多元生化实验的数字微流控芯片的单位时间具体为62.5ms。
按照上述步骤对图1所示的数字微流控芯片进行灾难性故障测试仿真,测试算法在Visual studio 2012环境下采用C++编程实现,得到的测试方法收敛示意图如图4所示,图4的横坐标为迭代次数,纵坐标为单位时间;图5中纵坐标为单位时间,横坐标为不同的测试方法;由图5可知,本实施例的测试算法的测试花费时间明显优于欧拉回路法,比蚁群算法的测试花费时间仅多1个单位时间。但是,单一的蚁群算法一般在迭代1350次左右收敛,由图4可知,本实施例的方法在950次左右算法收敛,相比单一的蚁群算法收敛性提了29%,方法的收敛性更好,在保证了测试花费时间较低的情况下,能够快速地求得较优的测试路径。
由于汉密尔顿回路测试法、分区子阵列合并调度测试法无法检测出相邻电极短路故障,并行测试和自建自测试法只能用于规则阵列的芯片测试,这些测试方法缺少全面性、兼容性,本实施例的测试方法不与这些测试方法作比较。
- 还没有人留言评论。精彩留言会获得点赞!