并联机器人工作空间的求解方法与流程

本发明涉及并联机器人技术领域，具体涉及一种求解并联机器人工作空间的方法。

背景技术：

并联机器人(也称并联机构)应用领域包括：运动模拟器、虚拟轴机床、微操作机器人、并联力传感器、空间飞行器的对接装置、天文望远镜的姿态控制器等等。在所有这些应用中，都离不开对并联机构工作空间的研究。工作空间是衡量机器人性能的重要指标，所有并联机器人都需要更为精确和详尽的工作空间描述。

并联机器人的工作空间是指其末端执行器的工作区域，是衡量机器人性能的重要指标之一。并联机器人工作空间的求解方法主要有两类：解析法和数值法。解析法的代表为几何法，它利用曲面包络原理求解各支链空间边界，再利用曲面求交获得实际工作空间，但是这种方法求解复杂难以实现。数值法是在空间中进行扫描，利用机构的逆解获得当前位姿对应的结构参数，以边界约束条件为判定依据从而获得所有边界点的方法，但是传统的数值方法并不能反映运动平台具有一定姿态调整能力下的工作空间。

因此，如何对传统的数值方法进行改进，以反映运动平台具有一定姿态调整能力下的工作空间。

技术实现要素：

本发明要解决的技术问题是提供一种求解并联机器人工作空间的方法，且该方法能够反映运动平台具有一定姿态调整能力下的工作空间。

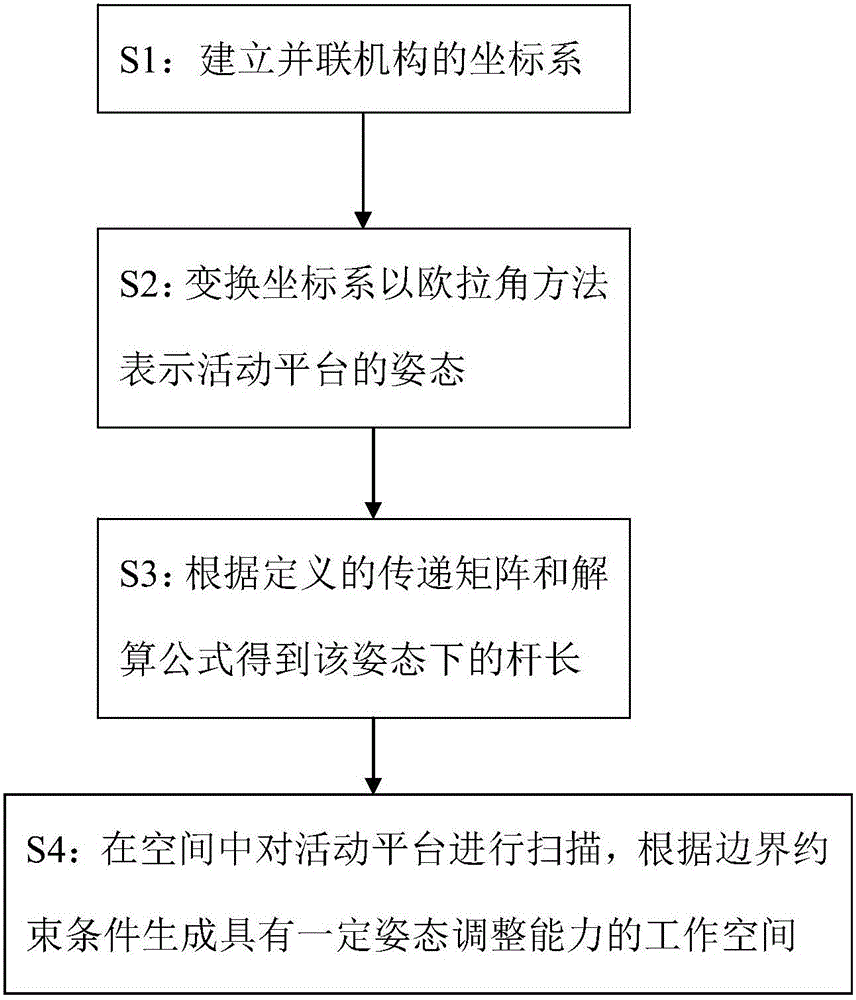
为解决上述技术问题，一种求解并联机构工作空间的方法，其特征在于，所述方法包括：步骤一：建立并联机构的坐标系，定义出并联机构的活动平台坐标系{P}:O_p-X_pY_pZ_p和并联机构的固定平台坐标系{B}:O_b-X_bY_bZ_b；步骤二：变换坐标系以欧拉角表示活动平台的姿态；步骤三：在以欧拉角方法表示活动平台的姿态下，根据定义的传递矩阵和解算公式得到该姿态下的并联机构的杆长；步骤四：对活动平台进行空间扫描，根据边界约束条件生成具有一定姿态调整能力的工作空间。

优选的，所述步骤二包括将活动平台坐标系{P}:O_p-X_pY_pZ_p的当前姿态用初始与固定平台坐标系{B}:O_b-X_bY_bZ_b重合的坐标系进行三次有顺序的旋转。

优选的，三次旋转的顺序为：(1)绕{P}坐标系的Z_p轴旋转角ψ，ψ为最终Z_p在{B}中X_bY_b平面内的投影与X_b的夹角；(2)绕{P}坐标系的Y_p轴旋转角θ，θ为最终Z_p在{B}中与Z_b的夹角；(3)最后再绕{P}坐标系的Z_p轴旋转角φ。

优选的，所述步骤三中的传递矩阵具体公式为

其中，φ、θ、ψ为欧拉角中的自旋角、章动角和进动角。

优选的，所述步骤三中的解算公式具体为

优选的，所述步骤四中的边界约束条件具体指杆长极值。

优选的，所述杆长极值包括杆长极大值和杆长极小值。

优选的，所述步骤四中空间扫描的扫描方式，采用柱坐标的极角和极径的方式在空间中进行扫描，直至探测出空间中所有的边界。

优选的，所述步骤四的具体流程为：利用柱坐标系的方式构造扫描空间，在高度上以微小步长将搜索空间分割为若干个平行的扫面平面；在每个扫面平面上以极坐标的方式，使活动平台中心点坐标的极径和极角分别从0开始逐渐增大；由步骤三计算得到每个扫描点对应位置的各个杆长长度l'；根据杆长约束条件l_min≤l_i≤l_max判断是否仍在工作空间范围内，若超出的话记录边界点；依次搜索出各个扫描截面上的边界曲线，进而得到整个工作空间。

优选的，在每个扫面点添加灵活姿态角判断的扫描，即令章动角θ为特定值，进动角ψ从0°到360°进行姿态扫描，为了限制运动平台自身的转动，令进动角等于自旋角的负数，即ψ＝-φ。

本发明提出的求解并联机构工作空间的方法解算效率高，能够得到活动平台具有一定姿态调整能力下的工作空间，对于并联机构的设计和应用具有一定的指导意义。

下面结合附图和具体实施方式对本发明作进一步详细的说明。

附图说明

图1(a)是本发明第一实施例并联机构的俯视示意图；

图1(b)是图1(a)实施例并联机构的侧视示意图；

图2是求解并联机构的工作空间的流程图；

图3是第一实施例中活动平台姿态欧拉角表示方法示意图；

图4是第一实施例中活动平台工作空间扫描示意图。

具体实施方式

机器人的工作空间是机器人操作器的工作区域,它是衡量机器人性能的重要指标之一。在并联机器人设计中,工作空间是重要的指标,它决定着并联机器人的整体尺寸。

本发明以6自由度并联机器人为例，图1(a)是本发明实施例并联机构的俯视示意图，图1(b)是本发明实施例并联机构的侧视示意图。并联机构100包括固定平台10和活动平台20，固定平台10和活动平台20之间用六根可伸缩的杆件(A1B1,A2B2,A3B3,A4B4,A5B5,A6B6)相连接。固定平台10与杆件之间用球铰连接，活动平台与杆件之间也用球铰连接。在图1中，A1、A2、A3、A4、A5、A6分别表示活动平台20上的球铰连接，分别分布在半径为r的圆上。在图1中，B1、B2、B3、B4、B5、B6分别表示固定平台10上的球铰连接，分别分布在半径为R的圆上。六根杆件上分别装有直线电机作为驱动器,当杆件伸缩时,活动平台20便可以得到不同的位置和姿态。

图2为求解上述6自由度并联机器人的工作空间的流程图，下面结合具体实施例对其进行说明。

步骤S1:建立并联机构的坐标系，固定平台10的坐标系{B}:O_b-X_bY_bZ_b和活动平台20的坐标系{P}:O_p-X_pY_pZ_p。在该步骤中定义出活动平台20和固定平台10的坐标系表达方法。

继续参考图1，以固定平台10为原点建立空间直角坐标系{B}:O_b-X_bY_bZ_b，相应地，活动平台20所对应的空间直角坐标系为{P}:O_p-X_pY_pZ_p。在该并联机构等效模型中，A1、A2、A3、A4、A5、A6分别表示活动平台20上的球铰连接，分别分布在半径为r的圆上。B1、B2、B3、B4、B5、B6分别表示固定平台10上的球铰连接，分别分布在半径为R的圆上。其中，h为等效并联机构模型活动平台20距离固定平台10的高度，l_i为等效并联机构模型中杆件的杆长(i＝1,2,..6)。

步骤S2:变换坐标系以欧拉角方法表示活动平台20的姿态。通过变换坐标系以欧拉角表示活动平台20的姿态，再根据定义的传递矩阵和解算公式得到该姿态下的杆长。

变换坐标系的具体方法如下所示：将活动平台20的坐标系{P}:O_p-X_pY_pZ_p的当前姿态用初始与固定平台10的坐标系{B}:O_b-X_bY_bZ_b重合的坐标系通过三次有顺序的旋转而来。三次旋转的顺序为：(1)绕{P}坐标系的Z_p轴旋转角ψ，ψ为最终Z_p在{B}中X_bY_b平面内的投影与X_b的夹角；(2)绕{P}坐标系的Y_p轴旋转角θ，θ为最终Z_p在{B}中与Z_b的夹角；(3)最后再绕{P}坐标系的Z_p轴旋转角φ。ψ、θ和φ分别是是欧拉角中的进动角、章动角和自旋角。欧拉角的具体位置如图3所示。

步骤S3:在以欧拉角方法表示活动平台20的姿态下，根据定义的传递矩阵和解算公式得到该姿态下的杆长。具体求取杆长的过程如下所述：设活动平台20的坐标系原点O_P沿在固定平台10的坐标系X_b、Y_b、Z_b轴的移动量为x_p、y_p、z_p，欧拉角分别是ψ、θ和φ，则有如下关系：

式中：为A₁～A₆在固定平台10的坐标系{B}:O_b-X_bY_bZ_b下的坐标矢量，为A₁～A₆在活动平台20的坐标系{P}:O_p-X_pY_pZ_p下的坐标矢量，{P}:O_p-X_pY_pZ_p相对于{B}:O_b-X_bY_bZ_b的旋转变换矩阵为T：

各杆长l'的计算公式为：

步骤S4：在空间中对活动平台20进行扫描，根据边界约束条件生成具有一定姿态调整能力的工作空间。边界约束条件即为杆长极值，包括杆长的极大值和极小值。扫描方式采用柱坐标的极角和极径的方式在空间中进行扫描，直至探测出空间中所有的边界。具体的示意如图4所示，具体的流程描述如下：

步骤S41：利用柱坐标系的方式构造扫描空间，在高度上以微小步长将搜索空间分割为若干个平行的扫面平面；

步骤S42：在每个扫面平面上以极坐标的方式，使活动平台20中心点坐标的极径和极角分别从0开始逐渐增大；

步骤S43：由步骤S3中的式3计算得到每个扫描点对应位置的6个柔性支链长度l'。根据杆长约束条件l_min≤l_i≤l_max判断是否仍在工作空间范围内，若超出的话记录边界点。依次搜索出各个扫描截面上的边界曲线，进而得到整个工作空间。

在上述步骤中，优选的，为了限制活动平台20自身的转动，令进动角等于自旋角的负数，即ψ＝-φ。优选的，为了得到一定灵活姿态角的工作空间，在每个扫面点添加灵活姿态角判断的扫描，即令进动角ψ从0°到360°进行姿态扫描。

本发明提出的求解并联机构工作空间的方法通过用欧拉角表示运动平台的姿态，不仅使得解算效率高，也能够得到活动平台20具有一定姿态调整能力下的工作空间，对于并联机构的设计和应用具有一定的指导意义。

以上所述仅为本发明的实施方式，对于本领域的一般技术人员，依据本发明实施例的思想，在具体实施方式及应用范围上均会有改变之处，综上所述，本说明书内容不应理解为对本发明的限制。