一种采用随机数机制的动态可信度量方法与流程

本发明涉及可信计算领域中对动态可信度量，具体涉及一种采用随机数机制的动态可信度量方法。

背景技术：

为了解决计算机中高层应用存在的可信度和安全性度量的问题，许多学者已经提出了不少出色且符合可信计算标准的动态可信度量模型，并从一个或者多个角度检测和度量应用层上各类实体内的数据和行为的安全性，进而判断该实体是否可信。然而，部分模型的研究思路存在角度过于片面，计算结果集合{trust,suspicious,malicious}的判定条件不明确，计算方式过于复杂而导致时间性能降低等问题。

当前的可信计算领域中对动态可信度量的研究已经取得了相当大的进展，并且衍生出了不少第三方基本技术虽有差异但可信计算理论一致的优秀的动态可信度量模型。例如，一种经典的基于客户端/服务器的动态可信度量模型中，客户端发送一项服务请求给服务器端，而服务器在接收到这项请求后返回一个随机数值给客户端，当客户端获取到服务器端的响应之后，从TPM的PCR寄存器中提取出系统和应用的完整性度量值，采用shal摘要算法与随机数值一并签名返回给服务器端，最后，服务器采用一定的方式对完整性度量值做出检测，从而判断出应用的可信程度。

另有一种动态可信度量模型，它封装了比较常见的不安全的实体行为，从而形成了一个巨大的功能列表EL，这个列表就是作为处理多数不安全行为的方针和依据。

此外，还有一种非常依赖于硬件支持的动态可信度量模型，它从可信计算平台的可信根开始，自顶向下广度优先遍历整棵结点树，对每一个结点做一一检测，通过这种硬件层的检测方法来支撑起上层应用的动态可信度量。

当然，还有其它许多出色的动态可信度量模型，实际上，多数度量模型离不开PCR寄存器对动态可信度量的完整性度量值进行存储，完整性数据的存储包括完整性度量值本身的存储和哈希链接表的存储，前者被保存在磁盘上，后者则保留在PCR寄存器中，作为指向完整性度量值的指针或者索引，这样做的一个好处是降低内存的消耗，因为完整性度量值并不直接入驻内存。除此之外，匹配在动态可信度量模型也用得非常多，例如，完整性度量值和完整性标准摘要值的比较，当前实体行为和EL表中记录的实体行为的配对，比较的结果同样也是作为判定可信程度的依据。

以上各种方法的缺点分别在于：

就基于客户端/服务器的动态可信度量模型来讲，它的侧重点还是偏向于服务器对客户端的安全性检测，也就是这种模型中，客户端并没有携带任何动态可信度量的方法，它过分强调了降低甚至减少客户端对服务器的攻击，但却忽视了如何让源头(客户端)直接识别并消除不可信的行为，这样做的坏处是客户端越来越劣质，而服务器的品质却越来越高，而且每一次请求/响应所带来的时间和空间上的消耗是明显大于客户端自身去对自己的行为做检测所带来的消耗的，显然，这种做法在当下并不可取。再者，通过指针来操纵动态可信度量值，其危险性的存在也是不容忽视的。

而基于EL表的检测方式，在当今的动态可信度量模型中通常是一个必要的模块，它的处理方式非常简单，也容易应用，但最大的缺点就是，如果缺乏必要的方式来更新表内的行为，那么EL表将无法识别最新甚至复杂程度更高的不安全实体行为，那么最终的结果是这种动态可信度量的方式也会被淘汰。此外，EL表的判定仅有可信和恶意的判定，缺乏对某些更特殊的情况的判定，这种角度来看，它对计算结果的判定也是不完善的。

而比较依赖于可信根的度量方式实际上是从静态可信度量模型演化而来的，它作为动态可信度量模型的基础模块，和硬件配合非常良好，计算效率也非常高。然而，依据Dempster-Shafer原理中的信任衰减原则和信任聚合原则，这种广度优先遍历的搜索方式会导致数据在传递过程中发生损耗，那么检测结果的准确性也会大打折扣，单独依赖这种检测方式也是不可取的。

技术实现要素：

为了就客户端应用本身进行检测，避开请求/响应带来的性能消耗，同时，在传统的可信计算平台和EL表等的支撑下，以扩展出来的数据安全性校检区的作为补充，以随机数发生器作为模拟的平台，以概率计算理论作为可信计算的工具，通过将数据清晰的划分为可信，可疑和恶意三种状态，并结合给出的一系列判定规则，将数据的安全性判定作为一个必要的条件，从而在一定程度上判明实体的可信程度。

本发明的目的通过如下技术方案实现。

一种采用随机数机制的动态可信度量方法，包括如下步骤：

在可信计算平台上扩展出的数据校检模块即数据校检区，并在数据校检区的基础上引入随机数发生器RAND()，用于随机模拟流通于实体内的在任意动态时刻产生的数据，产生的数据包括可信的、恶意的和可疑的；紧接着，结合一系列判定规则，去检测和判明当前的执行实体的可信度，从确定实体是否能以预期的方式达到预期的目标；所述一系列判定规则包括微观实体行为序列理论，数据安全映射规则，基于概率计算的动态可信度量规则和判定结果改变规则中的一种以上。

进一步地，数据校检区包括安全数据通过区、不安全数据校验区、可疑数据校验区和恶意数据校验区；将数据校检区补充到传统的可信计算平台上，得到了扩展后的可信计算平台。

进一步地，所述随机数发生器RAND()用于模拟产生在应用程序内流通的数据，随机数发生器的两个重要性质：

(1)、当RAND()不用于模拟实体内流通数据时，其本身产生的数据是没有任何意义的；

(2)、当RAND()用于模拟实体内流通的数据时，RAND()产生的数据将具有了类别之分，即模拟了流通在实体内的安全数据、可疑数据和恶意数据。

进一步地，所述随机数模拟是让随机数发生器RAND()与一个给定的应用程序关联起来，成为应用程序内的数据流通者，并在每时每刻产生实体内流通的数据，而这些数据因为关联而有了安全、可疑和恶意的分类，进而实现了数据模拟。

进一步地，借助扩展可信计算平台上的数据校检模块，动态度量当前实体的数据的安全性，进而判定实体的可信程度，将随机数发生器的种子设为当前时间，以体现实体不可信的发生时随机变化的，这时的随机数发生器可以表示为RAND(Seed(Current))。

进一步地，所述数据校检模块中，将数据划分为可疑数据和非可疑数据这两类，非可疑数据包括安全数据和恶意数据两类，对于可疑数据，用a[modify(a)]表示可疑数据，表示a可能发生意外改写，用表示非可疑数据，表示a没有被改写的可能，这样数据便做好了初步的分类；假设数据的安全性范围是Safety＝[s1,s2]。此后，数据分类就可以细化了，进而得到了提出扩展可信计算平台时的数据分类，显然是安全的，是恶意的,就是在前面做初次分类的时候提到的非可疑数据，则非可疑数据实现了安全与恶意的细化分类，而仍用a[modify(a)]来表示可疑数据。

所述进一步地，一系列判定规则中的判定结果改变规则是：在做好了数据分类之后，引入数据安全性映射的定义和表达，数据安全性映射是以当前实体的行为序列中某一动态时刻下的子行为数据集合为定义域，以数据安全性认证集合ST＝{safe,suspicious,malicious}为值域的特殊映射，数据安全性集认证集合与数据的分类有着一一对应的关系，则得到数据安全性映射的数学表示为：

另外，数据安全性映射应当与系统的监控区域建立起关联，这种关联建立的目的是为了妥善处理可疑数据，经过映射而被判定为可疑的数据，需要将其转移至监控区动态监视其动态改变，如果数据或数据组被改写并由数据安全性映射判定为安全数据，则可脱离监控区并转移至实体内流通，如果被判定为恶意数据，则撤销该数据的流通，恶意数据本身也将死亡于系统的监控区域或移入恶意数据校检区。

进一步地，所述恶意数据包括原本就是恶意的数据和经过监控区域的监控得知的由可疑数据转移而来的恶意数据，关联到一个随机数发生器，则有如下表达式：

malicious data＝RAND(Seed(Current))|malicious+(suspicious→malicious)，式中，malicious data的是恶意数据集合，RAND(Seed(Current))是随机数发生器的一个实例，表示以当前系统时间产生的随机数，这是一个变量，|后面的内容表示取值,malicious表示经过一次检测就被判定为恶意的数据值，suspicious->malicious表示经过一次检测不能判断为恶意数据，但在系统运行时被转化为恶意数据的可疑数据值，+表示并集，表示这两种情况都属于随机数发生器产生恶意数据的情况；

设数据安全性映射启动的次数为n，用一个计数器count()来记录恶意数据产生的次数，结合古典概型的理论，样本空间的基本事件总数为N(S)＝n，产生恶意数据这一事件的所包含的基本事件总数为:

count(maliciousdata)＝count(RAND(Seed(Current))|malicious+(suspicious→malicious))

伯努利大数定律指出，如果μ是n次独立试验中事件A发生的次数，且事件A在每次试验中发生的概率为P，则对任意正数ε，有：

因此，在该模型中，当n很大的时候，可以用频率表示概率，并可得知恶意数据产生的概率为：

P＝P(malicious data)＝count(malicious data)/n。

进一步地，系统(任何需要进行可信度量的计算机系统或者计算机应用程序)策略的制定者在可执行文件列表中写入每个可执行文件的预期容错概率P0，在传统的将可执行文件的完整性度量值和完整性标准摘要值比对的基础之上，并假设除数据之外的影响因素不存在，利用概率比对来得到可执行文件，或者说应用程序的可信度，并得到如下的动态可信度量规则，设当前运行的实体为A，则：

G(A)表示对实体的动态可信度量值，P是经过实验计算出来的恶意数据的概率，P0是一个计算机系统允许接受的容错概率的最大值，如果P<P0，判定系统不可信，即malicious，否则可信，即trust。

与现有技术相比，本发明具有如下优点和技术效果：

1、由于概率P是在可执行文件经过大量次数的运行之后得到的，它将会被写入可执行文件列表，这样，当某个恶意文件不小心被启动的时候，可以通过P和P₀的比较，即P＞P₀,跳过传统动态可信度量模型的繁琐计算过程，提高度量的效率。

2、该模型重视客户端应用的主动测量，减少了请求/响应机制下不必要的时间消耗。

3、在数据安全性校检区的引入和判定方面，亦是对EL表结果判定简单化这一缺点的改进。

4、此模型理论上仍需要借助硬件条件的支持，但它基本上摆脱了静态可信度量模型作为底层支撑，因而也不会存在数据在传递过程中的消耗问题。

附图说明

图1为实例中数据校检区的区域划分示意图。

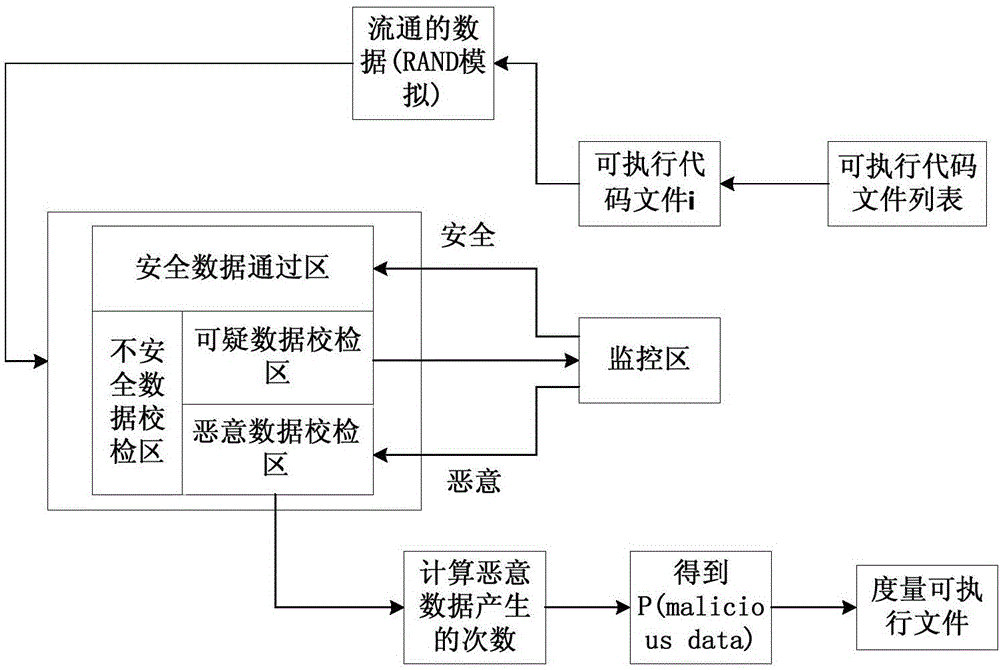
图2为实例中动态可信度量模型架构图。

具体实施方式

以下结合附图和实例对本发明的具体实施作进一步说明，但本发明的实施和保护不限于此，需指出的是，以下若有未特别详细说明之处，均是本领域技术人员可参照现有技术实现的。

对数据校检模块的引入应当基于对数据的分类，从大的方面来讲，计算机系统中的数据可以分为安全数据和不安全数据，不安全数据可进一步细分为可疑数据和恶意数据，这两类不安全数据是动态可信度量的“眼中钉”，它们都需要被及时处理以保证当前应用程序的安全运行。基于这种分类，将数据校检模块做出一个大致的划分，并将数据校检区补充到传统的可信计算平台上，得到了扩展后的可信计算平台，如图1所示。

而随机数发生器RAND()可用于模拟产生在应用程序内流通的数据，对于一个给定的实体来说，其中的数据完全符合之前提到的数据分类标准，即安全，可疑和恶意，在此给出随机数发生器的两个重要性质，这两个性质将指出随机数发生器和应用程序数据，或者说是和实体数据之间的模拟和对应关系。

RAND()的性质：

(1)、当RAND()不用于模拟实体内流通数据时，其本身产生的数据是没有任何意义的；

(2)、当RAND()用于模拟实体内流通的数据时，RAND()产生的数据将具有了类别之分，即模拟了流通在实体内的安全数据，可疑数据和恶意数据。

有了随机数发生器的性质之后，就可以给出在动态可信度量中应用的随机数模拟的概念了。所谓随机数模拟，就是让随机数发生器RAND()与一个给定的应用程序关联起来，成为应用程序内的数据流通者，并在每时每刻产生实体内流通的数据，而这些数据因为关联而有了安全，可疑和恶意的分类，进而实现了数据模拟。

前面已经提到，在排除数据以外的因素的条件下，动态可信度量的研究方法，更具体的说，是借助扩展可信计算平台上的数据校检模块，动态度量当前实体的数据的安全性，进而判定实体的可信程度，为了把动态和随机体现的更加全面，需要将随机数发生器的种子设为当前时间，以体现实体不可信的发生时随机变化的，这时的随机数发生器可以表示为RAND(Seed(Current))。

在提出扩展可信计算平台的概念的时候，就已经提到了数据可以划分为安全，可疑和恶意三类，可疑数据作为一种中间类型的数据自有其独特的意义，将可疑数据定义为与安全数据相似但却附带着修改行为的数据，附带着修改行为的意思就是当前这个数据虽然正常但是很有可能在被使用的时候发生修改，而修改的结果也无法预知，需要在监控区进行进一步的监控和判断。依据可疑这一中间角色，先将数据划分为可疑数据和非可疑数据这两类，毫无疑问，非可疑数据理应包括安全数据和恶意数据两类，对于可疑数据，用a[modify(a)]表示可疑数据，表示a可能发生意外改写，用表示非可疑数据，表示a没有被改写的可能，这样数据便做好了初步的分类。假设数据的安全性范围是Safety＝[s1,s2]。此后，数据分类就可以细化了，进而得到了在提出扩展可信计算平台时的数据分类，显然是安全的，是恶意的,就是在前面做初次分类的时候提到的非可疑数据，则非可疑数据实现了安全与恶意的细化分类，而仍用a[modify(a)]来表示可疑数据。

在做好了数据分类之后，就可以引入数据安全性映射的定义和表达了。数据安全性映射是以当前实体的行为序列中某一动态时刻下的子行为数据集合为定义域，以数据安全性认证集合ST＝{safe,suspicious,malicious}为值域的特殊映射，数据安全性集认证集合与数据的分类有着一一对应的关系，则可以得到数据安全性映射的数学表示为：

另外，数据安全性映射应当与系统的监控区域建立起关联，这种关联建立的目的是为了妥善处理可疑数据，经过映射而被判定为可疑的数据，需要将其转移至监控区动态监视其动态改变，如果数据或数据组被改写并由数据安全性映射判定为安全数据，则可以脱离监控区并转移至实体内流通，如果被判定为恶意数据，则撤销该数据的流通，恶意数据本身也将死亡于系统的监控区域或移入恶意数据校检区，这种关联在其它的动态可信度量模型中也经常用到，称为判定结果改变规则。

就数据分类的规则，数据安全性映射函数和判定结果改变规则来看，恶意数据应当包括原本就是恶意的数据和经过监控区域的监控得知的由可疑数据转移而来的恶意数据，关联到一个特定的随机数发生器，则有如下表达式：

malicious data＝RAND(Seed(Current))|malicious+(suspicious→malicious)

设数据安全性映射启动的次数为n，用一个计数器count()来记录恶意数据产生的次数，结合古典概型的理论，样本空间的基本事件总数为N(S)＝n，产生恶意数据这一事件的所包含的基本事件总数为:

count(maliciousdata)＝count(RAND(Seed(Current))|malicious+(suspicious→malicious))

伯努利大数定律指出，如果μ是n次独立试验中事件A发生的次数，且事件A在每次试验中发生的概率为P，则对任意正数ε，有：

因此，在该模型中，当n很大的时候，可以用频率表示概率，并可得知恶意数据产生的概率为：

P＝P(malicious data)＝count(malicious data)/n

到了这一步，还需要让系统策略的制定者在可执行文件列表(软件功能列表FL)中写入每个可执行文件的预期容错概率P0，在传统的将可执行文件的完整性度量值和完整性标准摘要值比对的基础之上，并假设除数据之外的影响因素不存在，利用概率比对来得到可执行文件，或者说应用程序的可信度，并得到如下的动态可信度量规则，设当前运行的实体为A，则：

动态可信度量模型架构如图2所示。

实验结果：本实例模型用一个简单的模拟实验来说明，具体到某一特定的上层应用可以制定出更加具体而复杂的可信度量策略，假设某一应用(这里不给出其功能)只接收正数，且一般的数据接收范围是(0，9)，小于0的数默认为恶意数据，可能出现的篡改行为假设为整型数据的字符化，此篡改行为将会被判定为可疑行为，由此接收的数据认定为可疑数据(一般其范围将大于9)，并需要由监控区进一步判定和处理，另外假设动态可信度量的标准概率为0.08，由于恶意数据产生的概率是大量实验得到的结果，这里仅通过一段动态时间内的100次实验来模拟说明，按照前面的计算公式，得到的实验结果如表1所示。

表1动态可信度量模拟实验结果

由表1可知，假设某一应用只接收正数，且一般的数据接收范围是(0，9)，小于0的数默认为恶意数据，可能出现的篡改行为假设为整型数据的字符化，此篡改行为将会被判定为可疑行为，由此接收的数据认定为可疑数据(数字字符的编码值一般大于9，但其表面上看与整型数据一样)，并需要由监控区进一步判定和处理，另外假设动态可信度量的标准容错概率为0.08，由于恶意数据产生的概率是大量实验得到的结果，这里仅通过一段动态时间内的100次实验来模拟说明，表中的前三行表示系统运行中的某三个时刻的过程，以第一行为例，当前随机发生器RAND()产生的数据为6，并且当前随机数发生器已经产生了11次数据了(即表示前面已经经过10次模拟，并且遭遇了一次攻击并将其截获)，数据(6)将进入运行的实体内流通，它在范围(0，9)内，属于安全数据，再来看最后一行，经过了大量实验(前面已经假设100次)，实时攻击频率为0.13，根据伯努利大数定律，以概率取代频率，就可得知0.13大于标准的标准容错概率0.08，可判定实体不可信。