基于PERT的项目进度跟踪调整方法及系统与流程

本发明涉及基于PERT的项目进度跟踪调整方法及系统。
背景技术：
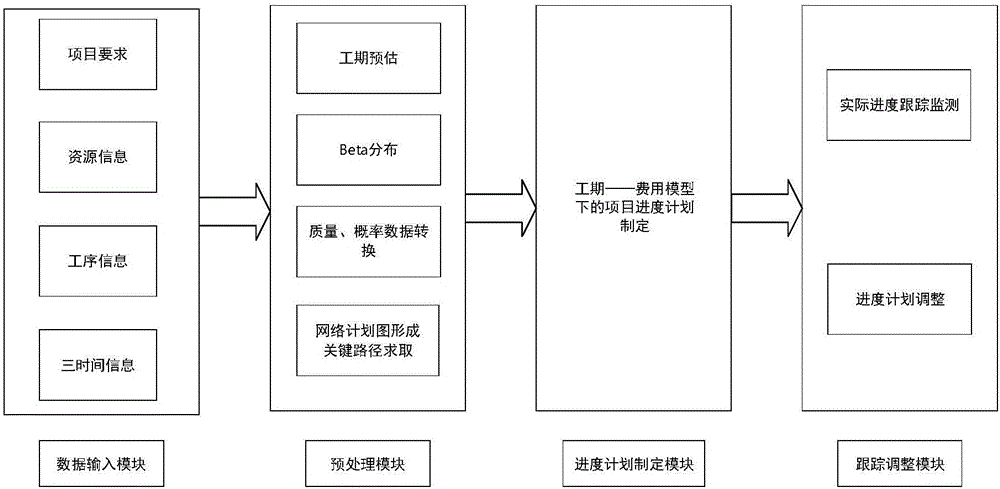
：随着现今项目业主对项目施工方要求越来越高，项目施工方为了保证项目按要求完成，必须制定合理的项目进度计划，另外实时跟踪项目的实际进度并及时纠偏调整。项目的计划制定和调整不可分割，但在现有方法或技术中，集中于对项目初期计划的制定，而调整计划多为启发式并依赖于施工方的经验，缺乏与计划制定的联动系统。在项目进度计划制定的方法中，PERT(计划评审技术)有着广泛应用。PERT是考虑了工期不确定性的网络计划制定及评价技术。其应用于施工项目进度计划制定的基本流程为，根据施工项目各工序间逻辑关系绘成网络图；在明确业主的项目工期期望后，对各工序工期进行预估，一般假设工期服从β分布，可利用三时估计法求出该分布；最后，以网络图中期望工期之和最大的路径或工序间总时差等于0的路径作为关键路径，得出进度计划。进一步可计算关键路径上各工序的机动时间，用来在项目后续进行中应对进度偏离。PERT存在对时间参数预估尺度把握不准而造成进度计划制定与实际进度偏差较大，以及未考虑资源约束对三个时间取值影响的技术问题。此外，项目进度的调整方法主要是对工序间时差或机动时间的利用。在大型施工项目中，由于施工网络图结构的复杂性，在进度的跟踪调整时，进度计划方法大都采取启发式方法调整机动时间，效率低下，合理性较差，缺少对项目整体的考虑。技术实现要素：针对经典PERT存在的上述不足，本发明提出基于PERT的项目进度跟踪调整方法及系统；在保留预估工期服从β分布的假设下，基于时间参数的意义和实际情况，对时间参数的选取尺度进行了明确；并将资源约束作为预估工期对应的概率指标结合到最乐观时间的取值中，体现了对工期分配的限制；最后，结合约束理论松弛资源约束的思想并考虑质量要素，建立费用——工期线性模型，形成了满足质量要求、尽量提前完工、实现费用最低同时具有较高完工概率的基于改进时间参数预估的PERT进度计划制定。基于PERT的项目进度跟踪调整方法，所述方法由计算机程序控制计算机设备来完成，所述计算机设备包括存储器、处理器及存储在存储器上并可在处理器上运行的计算机程序；所述处理器执行所述计算机程序时实现以下步骤：数据输入步骤，录入项目基本信息，项目基本信息包括：对项目的质量要求转换概率要求、工序划分与工序逻辑关系、项目物料信息、三时估计法预估的三个时间信息；预处理步骤，处理预估的时间参数得到对应β累计概率分布参数、将数据录入中对项目的质量要求转换概率要求，利用β累计概率分布函数形成项目进度要求，即各工期约束，利用数据中工序信息形成施工网络计划图并得到关键路径；项目进度制定步骤，依据工期—费用模型的求解结果安排进度计划；跟踪调整步骤，对项目实际进度进行实时监控，对发生偏离的实际进度进行及时调整。基于PERT的项目进度跟踪调整方法，所述方法由计算机程序控制计算机设备来完成，所述计算机设备包括存储器、处理器及存储在存储器上并可在处理器上运行的计算机程序；所述处理器执行所述计算机程序时实现以下步骤：步骤(1)：录入施工项目的基本信息；对施工项目各工序时间参数采用改进的PERT中的三时估计法对三个时间进行预估，并录入预估结果；改进的PERT三时估计法中对应的三个时间是指：考虑资源分配的最乐观时间a、最悲观时间b和最可能时间m；数据录入完毕后执行预处理操作，选取按最悲观时间b计算的总工期最大的一条施工路径作为关键路径；所述基本信息包括工序划分和工序逻辑关系；步骤(2)：利用步骤(1)预估的三个时间以及三个时间固定概率拟合β累计概率分布函数：根据各工序固定概率P＝[P(a),P(m),P(b)]及其所对应的预估工期t＝[a,m,b]，拟合出β累计概率分布函数且使其拟合方差Δε最小，进而得到拟合出的β累计概率分布参数r和s；步骤(3)：依据最悲观和最乐观时间对完工概率的限制P(ai)≤Pi≤P(bi)，对项目保证质量情况下的完工概率要求Pi≥PQi，将P(ai)、P(bi)和分别代入步骤(2)的β累计概率分布函数中一一对应求解t(ai)、t(bi)和形成工期约束，并结合项目管理部门对机动时间N的要求构建费用—工期线性优化模型，求解在最悲观时间上可压缩工期；步骤(4)：在步骤(3)所得到最悲观时间上可压缩工期xi后，计算计划进度；工程项目按所述计划进度指导施工；步骤(5)：进入跟踪调整模块，对实际进度进行监测；步骤(6)：判断实际进度与计划进度偏差是否大于设定值；若否，则返回步骤(5)；若是就记录发生变动处工序序号为K；步骤(7)：根据实际施工资源的变动修正P(a)值，根据修正后概率P＝[P(a),P(m),P(b)]，重新预估a、m、b的值；步骤(8)：判断总工序的数目n是否大于K；若是就进入步骤(9)；若否表示项目处于最后验收工序阶段，限定在工序最后验收工序阶段上发生的偏离仅作一次调整：修正机动时间N值、重新预估修正工序n单位时间压缩费用Cn值；获取优化进度计划值，跟踪调整运行结束；步骤(9)：判断关键路径上可压缩工期总和是否小于N，若是就修正N值，且重新预估修正ci值，返回步骤(2)；若否，直接返回步骤(2)。所述步骤(1)中改进的PERT中的三时估计法对三个时间进行预估，第i个工序的最乐观时间ai为考虑资源分配的最少时间，按照完工概率P(ai)进行估算。Oi：第i个工序占用的资源数，资源指施工资源，例如不同工种的专业施工队；R：工程项目总资源数；P(ai)∈(0,1)；最可能时间m按照完工概率P(m)＝0.5进行估算；最悲观时间b按照完工概率P(b)＝0.95进行估算。所述步骤(2)的β累计概率分布函数：r和s：累计概率分布模型未知形状参数；拟合方差Δε：所述步骤(3)的对项目保证质量情况下的完工概率要求下限：其中，PQi为业主对项目保证质量情况下的完工概率要求下限；Qi：施工质量的要求，可划分为多档次，如质量要求极高则设置Qi＝0.95、质量要求高Qi＝0.85、质量要求一般Qi＝0.75；ωi：质量完工概率间转换系数；费用—工期线性优化模型：约束条件包括工序工期可压缩水平的约束、保证质量下的可压缩工期约束和机动时间约束：xi≤t(bi)-t(ai)；其中，C：项目因压缩工期产生的总费用；Ci：工序i单位时间压缩费用，通过预估得到；xi：在最悲观时间上可压缩工期；t(ai)：最乐观时间的工期概率P(ai)对应于β累计概率分布下的工期；t(bi)：最悲观时间的工期概率对应于β累计概率分布下的工期；tQi：业主对项目保证质量的情况下完工概率要求下限PQi对应β累计概率分布下的工期；N：工程机动时间，用以应对突发或偏离计划的情况，根据实际进度调整。所述步骤(4)的计划进度的计算公式为：Hi＝bi-xi将计算得到的Hi值作为计划进度。所述步骤(8)及步骤(9)中，机动时间N值的修正根据实际进度调整，但必须满足以下两个条件：满足业主工期要求T，即为保证机动性，机动时间N值小于等于关键路径上最大可压缩工期和的80％，即基于PERT的项目进度跟踪调整系统，包括：存储器、处理器及存储在存储器上并可在处理器上运行的计算机程序；所述处理器包括：数据输入模块，用于录入项目基本信息，项目基本信息包括：对项目的质量要求转换概率要求、工序划分与工序逻辑关系、项目物料信息、三时估计法预估的三个时间信息；预处理模块，用于处理预估的时间参数得到对应β累计概率分布参数、将数据录入中对项目的质量要求转换概率要求，利用β累计概率分布函数形成项目进度要求，即各工期约束，利用数据中工序信息形成施工网络计划图并得到关键路径；项目进度制定模块，用于依据工期—费用模型的求解结果安排进度计划；跟踪调整模块，用于对项目实际进度进行实时监控，对发生偏离的实际进度进行及时调整。本发明的有益效果：1本发明可实现对工序三个时间参数的科学预估与项目进度计划的合理制定；2本发明可实现与计划制定形成联动的项目进度的实时跟踪调整；3本发明中进度计划制定和跟踪调整不受施工网络图结构的复杂程度影响。附图说明图1为本发明系统结构图图2为本发明的总体流程图；图3为进度计划制定算例流程图；图4为进度计划制定算例下经典PERT与改进方法进度衡量指标概率对比图。具体实施方式下面结合附图与实施例对本发明作进一步说明。本发明系统结构如图1所示。结构分为数据输入模块、预处理模块、进度计划模块以及跟踪调整模块。图2为本发明的总体流程图，图3为进度计划制定算例流程图，如图所示。实现基于改进时间参数预估的PERT进度计划制定方法的具体步骤如下：1)对某项目单代号网络计划图的各工序工期按最悲观工期b进行预估，选取总工期最大的一条施工路径作为关键路径，将得到的关键路径表示为1→2→3→4→5，关键工序流程图如图3所示，路径的节点标号表示的活动内容组成；2)对图3的进度计划制定算例流程图中的5个工序节点的另外两个时间值即最乐观a、最可能时间m也需进行预估；3)利用三个时间固定概率拟合β累计分布函数，即根据各工序固定概率P＝[P(a),P(m),P(b)]及其所对应的预估工期t＝[a,m,b]，在本发明算例中分别为(t1,P1)、(t2,P2)、(t3,P3)、(t4,P4)、(t5,P5)分别拟合出各工序的β分布且使其拟合方差Δε1、Δε2、Δε3、Δε4、Δε5最小，进而得到拟合出的β分布参数。算例估算时间、概率参数：表1三时间估算参数表节点编号P(a)taP(m)tmP(b)tb10.75330.5250.954020.37580.5100.951830.625140.5120.952040.625210.5180.95305030.550.959拟合得出的β累计分布参数：表2β累计分布参数表节点编号rs11.73111.311421.45741.431931.81281.558241.81281.5582510.26295.1974e+06其中，r、s：累计概率分布模型未知形状参数4)将估计出的三个时间及得到的β分布数据带入费用—工期线性模型求解在最乐观时间上可压缩工期：约束条件包括工序工期可压缩水平的概率约束、质量约束、管理部门所要求提前完工的工期约束：xi≤t(bi)-t(ai)xi≤t(bi)-tQi其中，Ci：工序i单位时间压缩费用，预估得到；xi：在P(bi)对应的时间bi基础上工序i的可压缩工期；t(ai)：最乐观时间的工期概率P(ai)对应于β累计概率分布下的工期；t(bi)：最悲观时间的工期概率对应于β累计概率分布下的工期；业主对项目保证质量的情况下完工概率要求PQi对应β累计概率分布下的工期；Qi：质量要求；ωi：质量完工概率间转换系数；N：机动时间。对费用—工期线性优化模型中参数设定：表3费用—工期线性优化模型中参数表5)在算例中5个工序都求解出压缩工期xi后，利用xi求解进度计划Hi，进度计划求解公式：Hi＝bi-xi进度计划结果：表4进度计划结果6)本发明中发明方法的进度计划结果对比经典PERT进度计划结果：表5进度计划效果对照表本发明中发明方法得到的进度计划的完工概率与经典PERT进度计划得到的进度计划完工概率的比较如图4。通过算例比较结果显示：本发明方法中各工序H的和为92，经典PERT中各工序m的和为70，∑H明显大于∑m，在符合进度要求的同时留有了缓冲区N以供应对突发情况；而且H对应β概率分布中的概率多数情况下大于μ的概率，更符合对关键工序的完工预期；概率为0对应的计算工期，在经典PERT中略大于本发明方法中的计算值，但都贴近0；概率为1对应的计算工期，在经典PERT中明显大于改进方法中的计算值，且超出b较多，而本发明方法中的计算值较接近b，本发明方法更符合工期估计实际情况；本发明方法的计算方差远小于经典PERT中的计算方差。上述虽然结合附图对本发明的具体实施方式进行了描述，但并非对本发明保护范围的限制，所属领域技术人员应该明白，在本发明的技术方案的基础上，本领域技术人员不需要付出创造性劳动即可做出的各种修改或变形仍在本发明的保护范围以内。当前第1页1 2 3