用于实时应用的具有同时边缘伪像去除的二维离散傅里叶变换的制作方法

本发明涉及用于配置现场可编程硬件以去除二维离散傅里叶变换(2ddft)中的边缘效应或级数终止错误的方法和系统。本申请通过引用2015年7月20日提交的美国临时申请no.62/194,689的全部内容而并入于此。

背景技术：

离散傅立叶变换(dft)是具有广泛应用的最常用和最重要的函数之一，所述应用包括但不限于数字通信系统、图像处理、计算机视觉、生物医学成像以及从2d数据重建3d(例如，层析成像)密度。傅立叶图像分析通过将空域中的复卷积运算转换成频域中的简单乘法来简化计算。由于计算复杂性，dft经常成为针对需要高吞吐量和近实时运算的应用的计算约束。1965年首次提出的cooley-tukey快速傅里叶变换(fft)算法(nplno.1)将dft的复杂度从o(n²)降低到针对1ddft的o(nlogn)。然而，在2ddft的情况下，1dfft必须以二维方式进行计算，从而将复杂度增加至o(n²logn)，由此使2ddft成为实时机器视觉应用(nilno.2)的显著瓶颈。

存在2ddft的几个资源高效、高吞吐量实现。这些实现中的很多都是基于软件的，并且已经针对通用处理器(gpp)上的高效性能进行了优化，这样的示例有：intelmkl(nplno.3)、fftw(nplno.4)以及spiral(nplno.5)。关于gpp的实现可以容易地适应多种情况。然而，gpp消耗更多的功率，并且对于实时嵌入式应用不是理想的。也已经提出了几种基于专用集成电路(asic)的实现(nplno.6)，但因为不容易修改，因此asic实现不是图像处理系统快速成型的经济有效的解决方案。由于固有的并行性和重配置性，现场可编程门阵列(fpga)是用于加速fft计算的有吸引力的目标，因为fpga充分利用了fft算法本身的并行性质。在过去的几年中，已存在几个基于高吞吐量fpga实现。这些实现中的大多数依赖于通过行和列分解(rcd)来重复调用1dfft，并有效使用外部存储器(nplno.2、no.7及no.8)。它们中的许多实现了实时或近实时的性能(即，对于标准512×512图像来说，大于或等于每秒23帧)。

在计算2ddft时，假定图像是周期性的，但通常不是这种情况。图像的这种非周期性导致傅里叶变换中的伪像，这已知为边缘伪像或级数终止错误(seriesterminationerror)。这些伪像在频域中呈现为几个高幅度系数的十字，如在nplno.9和no.10中所见。这种边缘伪像可以传递至后续处理阶段，并可能导致对生物医学应用结果的严重误解。目前的2dfftfpga实现都没有直接解决这个问题。这些伪像通常在预处理期间，利用镜像、窗口化、补零或后处理(例如，过滤技术)而加以去除。这些技术通常是计算密集型的，涉及图像大小的增加，并且往往也倾向于修改该变换。最常见的方法是通过在角落像素处渐变(ramp)图像来缓慢衰减边缘。渐变通常通过变迹函数来实现，诸如tukey(锥形余弦)或hamming窗口的，其平滑地将强度降低至零。这种方法可以通过将窗口函数存储在查寻表(lut)中，并在计算fft之前将其与图像流相乘，而作为预处理操作在fpga上实现(nplno.10)。尽管这种方法对于小图像来说计算量不是很大，但它会不经意地从图像中去除必要信息，如果该图像与几个其它图像一起被进一步处理以重建被用于诊断或其它判定关键应用的最终图像，那么其可能会造成严重后果。另一种常见方法是将图像从n×n镜像成2n×2n。这样做会使图像变成周期性的，从而去除边缘伪像。然而，这不仅将图像大小增加了四倍，而且使变换变得对称，这产生不准确的相位分量。

大部分以前的基于rcd的2dfftfpga实现有两个主要的设计挑战：1)1dfft实现需要具有合理的高吞吐量并且资源高效；和2)外部dram需要具有高带宽并且被有效寻址，因为图像通常很大，并且在行和列1dfft运算之间需要中间存储。

在计算1d、2d或多维fft的同时去除边缘伪像强加了额外的设计挑战，而不管使用什么方法。然而，这些伪像必须在其中伪像可能被传播至下一级处理的应用中去除。

引文列表

非专利文献

npl1:cooley,jamesw.,andjohnw.tukey.analgorithmforthemachinecalculationofcomplexfourierseries.mathematicsofcomputation19.90(1965):297-301.

npl2:kee,h.,bhattacharyya,s.s.,petersen,n.,&kornerup,j.resource-efficientaccelerationof2-dimensionalfastfouriertransformcomputationsonfpgas.distributedsmartcameras,2009.icdsc2009.thirdacm/ieeeinternationalconferenceon.ieee,2009.

npl3:wang,endong,etal.intelmathkernellibrary.high-performancecomputingontheintelxeonphi.springerinternationalpublishing,2014.167-188.

npl4:frigo,matteo,andsteveng.johnson.fftw:anadaptivesoftwarearchitectureforthefft.acoustics,speechandsignalprocessing,1998.proceedingsofthe1998ieeeinternationalconferenceon.vol.3.ieee,1998.

npl5:puschel,markus,etal.spiral:codegenerationfordsptransforms.proceedingsoftheieee93.2(2005):232-275.

npl6:lenart,thomas,matsgustafsson,andviktorowall.ahardwareaccelerationplatformfordigitalholographicimaging.journalofsignalprocessingsystems52.3(2008):297-311.

npl7:uzun,isaservan,abbesamira,andahmedbouridane.fpgaimplementationsoffastfouriertransformsforreal-timesignalandimageprocessing.vision,imageandsignalprocessing,ieeproceedings-.vol.152.no.3.iet,2005.

npl8:yu,chi-li,etal.multidimensionaldftipgeneratorforfpgaplatforms.circuitsandsystemsi:regularpapers,ieeetransactionson58.4(2011):755-764.

npl9:he,dajun,andqibinsun.apracticalprint-scanresilientwatermarkingscheme.ieeeicip(1).2005.

npl10:bailey,donaldg.designforembeddedimageprocessingonfpgas.johnwileyandsons,2011:323-324.

npl11:moisan,lionel.periodicplussmoothimagedecomposition.journalofmathematicalimagingandvision39.2(2011):161-179.

npl12:hast,anders.robustandinvariantphasebasedlocalfeaturematching.patternrecognition(icpr),201422ndinternationalconferenceon.ieee,2014.

npl13:galerne,bruno,yanngousseau,andjean-michelmorel.randomphasetextures:theoryandsynthesis.imageprocessing,ieeetransactionson20.1(2011):257-267.

npl14:hovden,robert,etal.periodicartifactreductioninfouriertransformsoffullfieldatomicresolutionimages.microscopyandmicroanalysis21.02(2015):436-441.

npl15:kehtarnavaz,nasser,andsidharthmahotra.fpgaimplementationmadeeasyforapplieddigitalsignalprocessingcourses.acoustics,speechandsignalprocessing(icassp),2011ieeeinternationalconferenceon.ieee,2011.

npl16:elliott,chance,etal.nationalinstrumentslabview:aprogrammingenvironmentforlaboratoryautomationandmeasurement.journaloftheassociationforlaboratoryautomation12.1(2007):17-24.

npl17:caesar,greg,andmarkwetzel.pxiexpress:extendingbackplanesto6gbyte/swhilemaintainingbackwardscompatibility.autotestcon,2005.ieee.ieee,2005.

npl18:nationalinstrumentstechnicaldocument[online],devicespecificationsnipxie-7976r,niflexriofpgamoduleforpxiexporess.2014,available:http://www.ni.com/pdf/manuals/374545a.pdf(accessedon:16thjanuary,2015)

npl19:jung,hyunuk,andsoonhoiha.hardwaresynthesisfromcoarse-graineddataflowspecificationforfasthw/swcosynthesis.proceedingsofthe2ndieee/acm/ifipinternationalconferenceonhardware/softwarecodesignandsystemsynthesis.acm,2004.

npl20:eonicpowerfftasic[online].available:http://www.eonic.com/

npl21:kee,hojin,etal.systematicgenerationoffpga-basedfftimplementations.acoustics,speechandsignalprocessing,2008.icassp2008.ieeeinternationalconferenceon.ieee,2008.

技术实现要素：

技术问题

如上所述，去除边缘伪像的现有技术需要大计算资源，诸如大内存使用和许多1ddft例程调用，或者不能以方便实现的方式有效且充分地去除边缘伪像。至今，没有高效且有效的技术可用于去除用于实时应用的2d离散傅立叶变换的边缘伪像。

本发明的目的是提供一种用于实时去除2d离散傅里叶变换中的边缘伪像的高效且有效的方案和系统。

本发明的另一目的是提供一种可容易在2dfftfpga(现场可编程门阵列)中实现的、用于实时去除2d离散傅里叶变换中的边缘伪像的高效且有效的方案。

本发明的另一目的是提供一种包括其中实现了用于实时去除2d离散傅里叶变换中的边缘伪像的高效且有效的方案的fpga的2dfft系统。

问题的解决方案

为实现这些和其它优点并且根据本发明的目的，如具体实施和广泛描述的，在一个方面，本发明提供了一种对对象图像数据执行二维离散傅立叶变换的方法，该方法要在一个或更多个数字处理器中执行，该方法包括：步骤(a)，从所述对象图像数据提取边界图像数据；步骤(b)，通过对所述对象图像数据的每一行执行一维快速傅里叶变换并且对所述对象图像数据的每一列执行一维快速傅立叶变换，对所述对象图像数据执行二维快速傅立叶变换；步骤(c)，对所提取的边界图像数据执行简化的二维快速傅立叶变换处理，而不逐列执行一维快速傅立叶变换，以导出平滑分量的快速傅立叶变换，所述步骤(c)包括：仅对所提取的边界图像数据中的第一列矢量执行一维快速傅立叶变换；利用缩放的列矢量导出所提取的边界图像数据中的剩余列的快速傅立叶变换；以及对所提取的边界图像数据中的每一行执行一维快速傅立叶变换；以及步骤(d)，通过从由步骤(b)执行的所述对象图像数据的二维快速傅立叶变换减去在步骤(c)中导出的所述平滑分量的快速傅立叶变换，导出被去除了边缘伪像的所述对象图像数据的周期性分量的快速傅立叶变换。在该方法中，步骤(b)和步骤(c)可以并行处理。

在该方法中，所述一个或更多个处理器可以包括主计算机和连接至该主计算机的一个或更多个现场可编程门阵列(fpga)，并且步骤(a)和步骤(d)可以由所述主计算机执行，而步骤(c)和步骤(d)可以由一个或更多个fpga并行执行。

在另一方面，本发明提供了一种用于对对象图像数据执行二维离散傅立叶变换的系统，该系统包括：主计算机；以及通过总线连接至所述主计算机的一个或更多个现场可编程门阵列(fpga)，其中，所述主计算机从所述对象图像数据提取边界图像数据，其中，所述一个或更多个fpga(i)通过对所述对象图像数据的每一行执行一维快速傅里叶变换并且对所述对象图像数据的每一列执行一维快速傅立叶变换，对所述对象图像数据执行二维快速傅立叶变换，其中，所述一个或更多个fpga(ii)对所提取的边界图像数据执行简化的二维快速傅立叶变换处理而不逐列执行一维快速傅立叶变换，以导出平滑分量的快速傅立叶变换，所述处理包括：仅对所提取的边界图像数据中的第一列矢量执行一维快速傅立叶变换；利用缩放的列矢量导出所提取的边界图像数据中的剩余列的快速傅立叶变换；以及对所提取的边界图像数据中的每一行执行一维快速傅立叶变换，并且其中，所述主计算机通过从所执行的所述对象图像数据的二维快速傅立叶变换减去所导出的所述平滑分量的快速傅立叶变换，导出被去除了边缘伪像的所述对象图像数据的周期性分量的快速傅立叶变换。在这个系统中，所述主计算机可以被配置成控制所述一个或更多个fpga，使得(i)和(ii)并行处理。

在另一方面，本发明提供了一种用于对n维图像数据执行n维快速傅立叶变换的方法，其中，n是大于2的整数，该方法包括：将所述n维图像数据划分成多个二维图像数据；以及对所述多个二维图像数据中的每个二维图像数据执行根据上面阐述的用于对对象图像数据执行二维离散傅立叶变换的方法；以及根据对所述多个二维图像数据中的每个二维图像数据执行上述方法的结果，导出所述n维图像数据的所述n维快速傅立叶变换。按类似方式，上述系统可以被配置成，使得所述主计算机接收n维图像数据，其中，n是大于2的整数，并且将所接收的n维图像数据划分成多个二维图像数据；所述一个或更多个fpga对所述多个二维图像数据中的每个二维图像数据执行(i)和(ii)；并且所述主计算机根据通过所述一个或更多个fpga对所述多个二维图像数据中的每个二维图像数据执行的(i)和(ii)的结果，导出所述n维图像数据的所述n维傅立叶变换。

本发明的有利效果

根据本发明的一个或更多个方面，高效且有效地去除不然会在2dfft中产生的边缘伪像。具体来说，在一些实施方式中，与常规技术相比，在有效去除边缘伪像的同时，针对外部存取的访问和用于2ddft的1ddft处理显著减少。例如，在本发明的有效示例中，所需的1dfft调用次数减少，并且外部dram使用显著降低，这大大节省了计算资源。

本发明的附加或单独特征和优点在下面的描述中将加以阐述，并且根据该描述将部分地明白，或者可以通过本发明的具体实践而获知。本发明的目的和其它优点将通过在书面说明及其权利要求书以及附图中具体指出的结构认识到并获得。

要明白的是，前面的一般描述和下面的详细描述都是示例性和解释性的，并且旨在提供对如要求保护的本发明的进一步阐释。

附图说明

图1示出了处理前和处理后的图像，以及根据本发明的实施方式的相应傅里叶分量分布，其被应用于具有非周期性边界的示例性图像。1a)是具有非周期性边界的示例性图像。1b)示出了1a)的图像的2ddft。1c)是平滑分量的dft，即，来自1a)的图像的去除伪像。1d)是周期分量，即，被去除了边缘伪像的1a)的图像的dft。1e)示出了根据平滑分量的重建图像。1f)示出了根据周期性分量的重建图像。

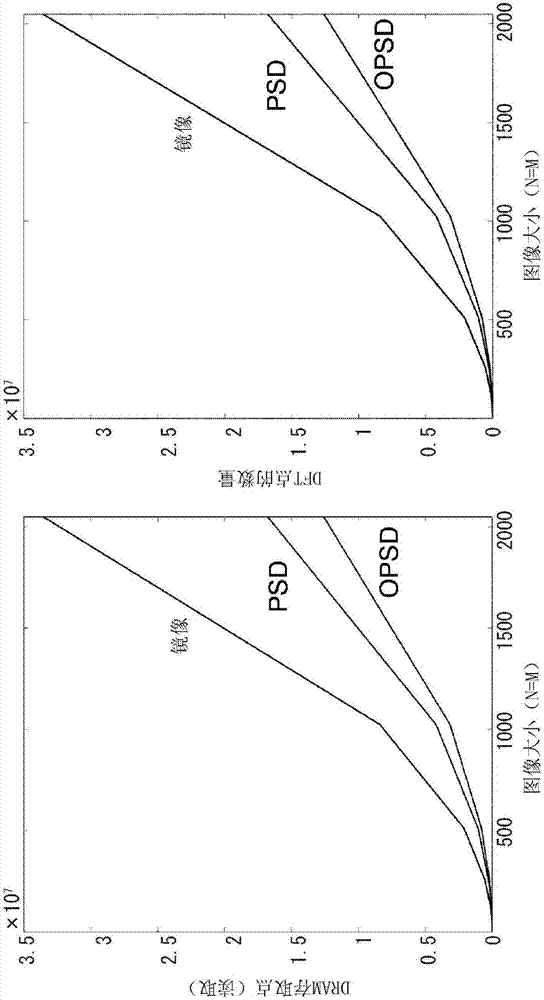
图2是分别示出根据本发明的实施方式的dram存取次数和要计算的dft点数的曲线图，其中，具有用于镜像、周期性加平滑分解(psd)及改进周期性加平滑分解(opsd)的图像大小增加。

图3是根据本发明的实施方式的基于pxie的多fpga系统的框图，该系统具有通过pxie机箱上的高速总线连接的主pc控制器。

图4是根据本发明的实施方式的具有ilut的2dfft的框图，示出了经由控制单元(cu)安排的外部存储器与本机存储器之间的数据传递。

图5是根据本发明的实施方式的基于pxie的2dfft实现的功能框图，其中利用改进的周期性加平滑分解进行同时边缘伪像去除。

图6示出了根据本发明的实施方式的总体硬件设计流程。dft是利用标准vhdl模块、翻转函数以及数学函数实现的。该翻转函数和数学函数在图7和图8中进行了详细描述，显示器a和显示器b分别示出原始和改进的dft，并且可以在单个或双显示装置上显示。

图7示出了翻转函数。图像的边缘按矢量存储，然后将其减去并对应地翻转。

图8示出了数学函数。已经利用标准cordic实现了余弦。

图9示出了分别针对该图像的原始图像、其dft、所计算的去除分量(rc)以及dft-rc。

具体实施方式

上面讨论的用于去除这些伪像的理想方法映射涉及在从图像去除最少量的信息的同时使图像周期性。为此，本公开使用基于高效周期性加平滑(“p+s”)分解(psd)的方法。由moisan(nplno.11)首次提出并在nplno.12、no.13及no.14中使用的psd是用于去除边缘伪像的理想方法，因为其不直接干扰除边界像素以外的其它像素并且不涉及增加图像的大小。此外，其在本质上是平行性质的，这使其成为基于高吞吐量fpga的实现的理想选择。本发明人已经显著改进了原来的p+s分解算法，使整体实现更加高效。具体来说，所需1dfft调用次数和外部dram利用率均显著降低，

在本公开中，为了快速建立算法原型，本发明人使用nationalinstrumentslabviewfpga2014(nplno.15)，这是一个鲁棒的基于数据流的图形设计环境(nplno.16)。labviewfpga提供与基于nationalinstruments(ni)xilinx的可重配置硬件的集成，允许与主机进行高效通信和通过pxie总线在多个fpga之间的高吞吐量通信(pciextentionsforindustryexpress)(nplno.16)。labviewfpga还使我们能够集成外部硬件描述语言(hdl)代码，并使我们能够灵活地扩展未来处理阶段所公开的设计。本发明人使用nipxie7976r(nplno.18)板，该板具有xilinxkintex7fpga和2gb高带宽外部存储器。然而，本公开中呈现的改进和设计可伸缩为任何可重配置的基于计算的系统。

本公开被组织如下：下一章节i描述利用周期性加平滑分解的边缘伪像去除。然后，章节ii描述了针对p+s分解的改进，根据本发明一实施方式，这导致fft调用的数量减少和对外部存储器的更少访问。章节iiia描述了硬件设置，而章节iiib描述了在所使用的硬件的背景下改进的p+s分解的架构的实施方式，以及如何将其推广到进一步的处理阶段和各种应用以及实验结果。

<i.用于边缘伪像去除的周期性加平滑分解>

周期性加平滑分解(psd：periodicplussmoothdecomposition)涉及将图像分解成周期性和平滑的分量；平滑分量从图像的边界计算，然后从图像中减去以得到周期性分量。在有限域ω＝{0、1、…、n-1}×{0、1、…、m-1}上具有离散n乘m灰度级图像i。i的离散傅立叶变换(dft)被定义为

这等同于矩阵乘法wiv，其中，

并且

v具有与w相同的结构，但是具有m维。因为wk具有周期n，这意味着wk＝wk+ln，l∈n，并因此，

因为一般来说，i不是(n,m)周期性的，所以具有存在于dft中的、源自如图1中的b)所示图像的相对边缘之间的明显不连续性的高振幅边缘伪像。moisan(nplno.11)提出了将i分解成周期性分量p(其是周期性的并且捕捉具有全部高频细节的图像本质)以及平滑变化的背景s(其再造边界的不连续性)。因而，i＝p+s。周期性加平滑分解可以通过首先构造边界图像b＝r+c来计算，其中，r表示按行转换时的边界不连续性，而c表示按列进行转换时的边界不连续性。

可以看出，边界图像b的结构非常简单，仅在边缘处具有非零值，如下所示。

可以通过下面的公式发现平滑分量s的dft。

然后，去除了边缘伪像的图像i的dft为

图1示出了处理前和处理后的图像i，以及根据本发明一实施方式的相应傅里叶分量分布，其被应用于具有非周期性边界的示例性图像。更具体地，1a)是具有非周期性边界的图像i。1b)示出了1a)图像的2ddft。1c)是平滑分量的dft，即，来自1a)的图像的去除伪像。1d)是周期分量，即，1a)被去除了伪像的图像的dft。1e)示出了根据平滑分量的重建图像。1f)示出了根据周期性分量的重建图像。

如图中所示，在重建时，显然a)的实际图像与f)的周期性重建图像之间的视觉差异可以忽略不计。下面的算法1总结了整个p+s的实现。有几种排布该算法的方法。在本公开中，其被排布成，使得周期性分量和平滑分量的dft容易用于进一步的处理阶段。对于最佳结果来说，周期性分量和平滑分量均应经历相似的处理阶段，并且应当在显示结果之前被重新加回去。然而，根据应用，平滑分量可能被完全丢弃。

<ii.针对fpga实现的psd改进>

本公开提供了原始p+s算法的显著改进，使得其可以在fpga上进行有效配置。如下所述，作为本公开中提供的这种独特改进的结果，1dfft调用的数量和外部dram的利用率都大大降低。上面的算法1指示需要针对每个图像帧(即，对于原始图像i和边界图像b)计算两个2dfft。尽管这些fft可以并行计算，但它们将需要大量的1dfft调用和针对外部存储器的重复访问。

在检查上面的方程(6)时，本发明人已认识到，边界图像b在边界行和列上彼此代数非(algebraicnegation)的意义上是对称的。b一共有n+m-1个独特的元素，相对于列和行在角之间具有以下关系。

b11＝r11+c11

b1m＝r1m+c11

bn1＝-r11+cn1

bnm＝-r1m-cn1(8)

在计算b的fft时，通常是先逐列进行1dfft，然后逐行进行1dfft，或者先逐行进行1dfft，然后逐列进行1dfft。长度为n的列向量v的fft为wv，其中，w在方程(4)中给出。矩阵b的按列的fft然后如下给出。

关于用b·1表示的第一列，这个矢量的1dfft如下。

可以示出，列j∈{2、3、…、n-1}的1dfft如下。

最后一列b·m的1dfft如下。

因而，矩阵b的按列的fft如下。

为了计算矩阵b的逐列的1dfft，只需要计算第一个矢量的fft，然后使用恰当缩放的矢量v来导出其余列的fft。逐行的fft必须正常计算。算法2给出了用于计算的捷径的总结。

算法2中提出的步骤取代了算法1的步骤13。通过减少针对边界图像的逐列1dfft计算，这种方法可以显著减少1dfft调用的次数，并减少针对基于fpga的实现的dram访问。这可以通过将初始矢量和缩放因子b1j临时存储在块ram/寄存器存储器中来实现，从而大幅减少dram存取并降低所需1dfft调用次数。

对于nxm图像来说，上述技术可以在计算2dfft的逐列分量的同时，将dram存取从4nm个点减少到3nm+n+m-1个点，并且将1dfft调用的数量减少到1个列向量而不是m个列向量。换句话说，要计算的dft点的数量可以从4nm减少到3nm+m。表i示出了关于dram存取点(读取)和dft点对镜像、p+s分解(psd)及改进p+s分解(opsd)的本实施方式的比较。镜像已被用于比较目的，因为它是另选技术之一，其在保持最大幅度信息的同时去除了边缘伪像。然而，由于图像的复制，因而大部分相位信息丢失。

图2是分别示出根据本发明的实施方式的dram存取次数和要计算的dft点数的曲线图，其中，具有用于镜像、周期性加平滑分解(psd)及改进周期性加平滑分解(opsd)的图像大小增加。如图2所示，与常规镜像和pds相比，根据本发明的实施方式的改进psd方法可显著减少从外部存储器读取并减少所需dft计算总数。表i比较镜像、psd和opsd

<iii.改进的psd的fpga实现>

<a.硬件设置>

因为2ddft通常被用于在复杂图像处理和机器视觉系统中简化卷积运算，所以本发明人已将该设计在可扩展用于下一级处理的系统上原型化为本发明的一个工作例。图3是根据本发明的实施方式的基于pxie的多fpga系统的框图，该系统具有通过pxie机箱上的高速总线连接的主pc控制器。根据本发明的实施方式，为了所提出的改进周期性加平滑分解算法的快速原型化，使用基于pxie(pciextentionsforindustryexpress)的可重配置系统。pxie是具有增强总线结构的pci系统的工业扩展，其为每个连接装置提供了4gb/s的最大吞吐量的专用总线访问。这允许主pc与几个fpga之间的高速专用链路。labviewfpga图形设计环境可以被用于复杂信号和图像处理系统的快速原型化。其使得能够在单一平台上有效地集成外部hdl代码和labview图形设计。在作出工作例方面，本发明人使用了flexrio(灵活可重配置的i/o)fpga板，其被插入pxie机箱。pxieflexriofpga板灵活并且可以被用于实现高吞吐量，因为它们允许多个fpga之间以高达1.5gb/s的速率的直接数据传递。这可以显著简化通常经由主pc进行通信的多fpga系统。该特征允许我们的系统扩展至进一步的处理阶段，使其适用于多种应用。图3示出了基于pxie的多fpga系统的基本概图，其中，主pc控制器通过pxie机箱上的高速总线连接。使用了nipxie-7976rflexrio板，其具有kintex7fpga和2gb外部dram，数据带宽高达10gb/s。该fpga板连同pxie-8135corei7pc控制器一起插入pxie-1082机箱。

<b.基本架构>

根据上面讨论的算法1和2，本实施方式的实现可以分解成四个阶段：1)计算一图像帧2dfft；2)计算边界图像；3)计算边界图像的2dfft并计算平滑分量；以及4)从原始图像的2dfft中减去平滑分量以导出周期性分量。在所有步骤当中，瓶颈将在于2dfft计算中。

fpga上的大多数2dfft实现使用行和列分解(rcd)与中间外部dram存储。基于rcd的2dfft的加速通常取决于被用于逐列和逐行1dfft计算的1dfft的吞吐量。n×m图像的这个rcd需要计算n个行和m个列的1dfft。这意味着在第一(行或列)计算之后，必须存储mn(或者如果m＝n，则为n²)个值。因为2dfft通常针对大图像进行计算，其无法被存储在有限的嵌入式块ram中，所以必须使用外部存储器。因此，加速还取决于外部存储器的带宽和有效寻址。对于小尺寸图像来说，与外部存储器相比，可以使用经由寄存器实现的块ram或存储器(nplno.19)。寄存器存储器通常更快且更易于使用，因为不同于外部存储器，其在可用通道数和带宽方面没有限制。然而，这种方法是资源昂贵的，并且如果图像很大，则会导致消耗大量的fpga资源。uzun(nplno.7)介绍了一种具有共享外部ram的几个1dfft处理器来进行实时2dfft计算的架构。

对于根据本发明的实施方式的2dfft实现来说，本发明人还使用了基于具有多核1dfft的rcd的方法。针对1dfft实现，本发明人使用了由hojin首先提出的内环展开技术(ilut)(nplno.20)，并且还用于2dfft设置(nplno.2)。长度为n的1dfft具有logn个fft级，并且每级具有n/2个蝶形单元。ilut涉及通过并行地执行几个蝶形单元来展开单个fft阶段(nplno.2)。图4示出了根据本发明的实施方式的具有ilut的2ddft的框图，示出了经由控制单元(cu)布置的外部存储器与本机存储器之间的数据传递。摄像头与fpga之间的数据通过利用dma(直接存储器存取)fifo而经由pc控制器传递。然而，也可以通过利用摄像机链路前端将数据直接传递至fpga。图4所示的本机存储器被用于缓冲外部存储器与1dfft核心之间的数据。这个本机存储器被划分成读取组件和写入组件，并且利用fpga片(slice)来实现。这节省了用于临时存储为计算边界图像的2dfft所需的矢量的块ram(bram)。控制单元(cu)组织调度在本机存储器与外部存储器之间传递数据。

边界图像的2dfft还需要通过行和列分解来计算。然而，如以数学方式所示，可以通过计算第一(边界)矢量的1dfft来计算初始的按行的fft，并且可以通过恰当缩放该矢量来计算扩孔矢量(reamingvector)的fft。在pc控制器中计算边界图像。但是该整个图像不需要传递至fpga。需要用于第一列和最后一列的1dfft计算的边界列向量。对于第一列与最后一列之间的每一列的1dfft，还需要边界行矢量来进行的恰当缩放。为了最小化主机与fpga之间的数据传递，本实施方式在经由dmafifo传递的每个图像帧的末尾处关联一额外行和列向量。因而，在传递n×m图像帧时，从pc控制器发送的数据点的量是nm+n+m。

边界图像的行和列矢量被存储在块ram(bram)中，而图像帧被直接存储到外部dram中。这使得边界图像的逐列1dfft计算能够与实际图像的fft计算并行进行。控制单元安排外部存储器与本地存储器之间的所有读写操作。图5示出了如上所述根据本发明实施方式的具有改进psd处理的总体2dfft的功能框图。更具体地，示出了上述根据本发明实施方式的基于pxie的2dfft实现的功能框图，其中利用改进的周期性加平滑分解进行同时边缘伪像去除。在主pc上进行两个图像的相减，以最小化存储器冲突，并在每个帧变得可用时访问该帧的周期性和平滑分量。

常规的基于rcd的2dfft硬件实现不使用周期性加平滑分解来同时去除边缘伪像。本发明的实施方式针对每个图像帧有效地执行双倍的1dfft计算量(针对原始和边界图像)，而与不同时执行边缘伪像去除的常规实现相比，仅需要较高运行时间的一小部分。如上例证，已经通过针对原始和边界图像的2dfft计算的并行化，并通过改进原始的周期性加平滑分解算法来减少外部dram存取，实现了这种加速。

如上所述，本公开提供了用于计算具有同时边缘伪像去除的高吞吐量2ddft的改进的基于fpga的方案。其基于周期性加平滑分解算法，其将2d图像的频域划分成具有高频十字形伪像的平滑分量，并且可以从原始图像的2ddft中减去，以获取无伪像的周期性分量。因为这种方法涉及同时计算两个2ddft，所以外部存储器寻址和重复的1dfft调用可能成为一个问题。为了解决这个问题，如上所述，本公开提供了用于改进原始psd算法的方案，该方案可以减少要计算的dft样本和dram存取的数量多达24％。根据本发明实施方式的技术利用在高速pxie总线上与主pc通信的xilinxkintex7fpga的广泛合成和基准测试来测试。所公开的系统可扩展以支持在高速总线上通信的几个fpga，并且对于大规模计算机视觉和生物医学应用来说可以是理想的。尽管将图像分解成周期性和平滑的频率分量，但与传统的基于fpga的2ddft实现相比，根据本发明实施方式的设计仅需要稍高的运行时间，并且可以被用于多种实时应用。

<本发明的实施方式的附加细节和其它变型例>

下面提供了本发明实施方式的一些附加细节和其它可能的变型例，其中一些已经在上面进行了描述。

本发明的一些实施方式利用labview2014创建并且利用labviewfpga模块2014进行测试。所用的fpga装置是xilinxvertix5；然而，该设计可以扩展至任何fpga模块。

图像采集是利用nationalinstruments(ni)视觉采集软件imaqvision完成的。图像从一个文件加载，但可以潜在地从摄像机或任何图像采集装置加载，只要支持imaq协议即可。

powerovercameralink(pocl)(另选图像采集软件)也可以被用作图像采集协议。

在本发明的实施方式中使用的离散傅里叶变换(dft)函数来自nationalinstruments，并且已经在labview2014中提供。然而，其可以被任何dftintellectualproperty(ip)块替换，以使总体设计更快。

图6示出了根据本发明的实施方式的总体硬件设计流程。dft利用标准vhdl块、翻转函数及数学函数来实现。显示器a和显示器b分别显示原始的和改进的dft，并且可以在单个或双显示装置上显示。

图7中示出了用于翻转函数的流程图。阵列索引、减去和替换阵列子集函数被用于直接在高速缓存存储器中翻转位置(如在nplno.11中所提到的)，以便减少存储器交换所需的总时间。

图8所示的数学函数计算必要的数学函数(包括除法、乘法、减法以及余弦)，并需要经傅立叶变换的翻转函数的输出作为输入。

数学函数中的余弦可以利用cordic(坐标旋转数字计算机)算法或基于lut(查找表)计算。

必须注意，图6中的虚线区表示并行操作。dft与翻转函数的dft并行计算，然后是上述数学函数。

图9示出了根据本实施方式的、分别针对该图像的原始图像、其dft、所计算的去除分量(rc)以及dft-rc。

本发明的这个实施方式是针对512×512的图像大小，但可以缩放至任何矩形大小。imaq显示被用于在屏幕上显示结果。

与3ghz的通用处理器(gpp)相比，公开的方案可以潜在地在少于1.5个时钟周期内计算改进的fft。然而，这个数字取决于所用的fpga的类型和所选的时钟周期。

本公开提供了一种新颖的基于fpga的设计来计算具有同时边缘伪像去除的高吞吐量2ddft。利用变迹函数或镜像去除这些伪像的标准方法因增加图像尺寸而涉及去除临界频率或者计算浪涌。本公开使用针对fpga实现改进的基于周期加平滑分解的伪像去除算法，同时仍然对512×512大小的图像流实现实时(即，等于或大于每秒23帧)的性能。本文所公开的方法导致外部存储器利用率的显著降低，从而避免了内存冲突，并简化了设计。本发明的实施方式利用与主pc通信的基于pxie的xilinxkintex7fpga系统进行了例证，这为进一步扩展用于各种工业应用的所公开方案提供了优势。

对于本领域的技术人员显而易见的是，在不脱离本发明的精神或范围的情况下，可以对本发明进行各种修改和变化。因此，本发明旨在覆盖落入所附权利要求书及其等同物的范围内的修改例和变型例。具体而言，明确地设想，上述实施方式及其修改例中的任两个或更多个的任何部分或全部可以被组合并被认为处于本发明的范围内。