自组织逻辑门和电路以及利用自组织电路解决的复杂问题的制作方法

相关申请的交叉引用本申请根据35u.s.c.§119以及所有适用的法律、法令和条约要求于2015年7月13日提交的第62/191,707号在先美国临时申请的优先权。本发明的领域包括数字电路及架构、混合模拟数字电路及架构以及神经形态电路及架构。实际应用包括具有通常依赖于昂贵近似的复杂问题的许多领域，包括计算机视觉、人工智能、大规模模拟(诸如，vlsi工具)以及加密的示例。
背景技术：
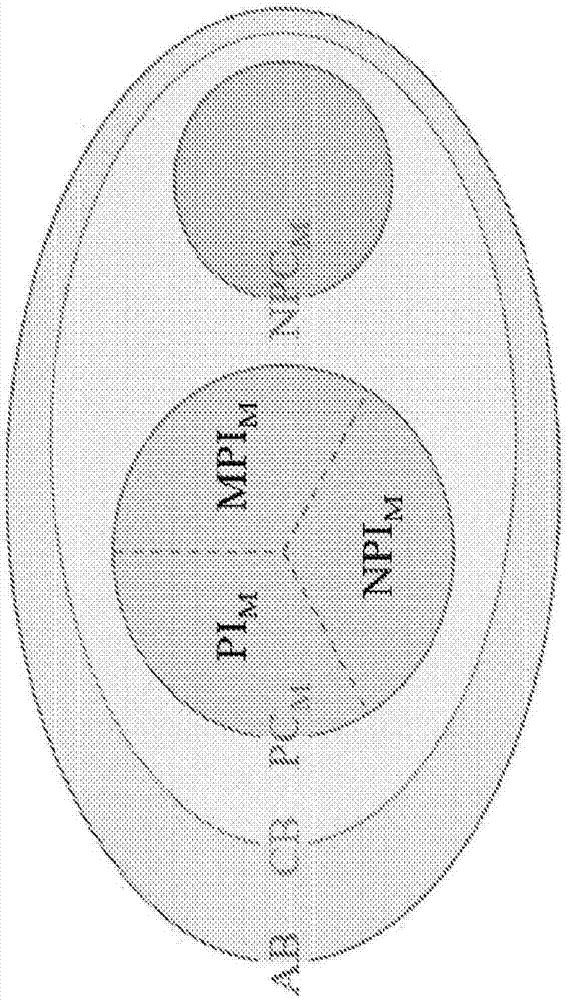
：多年来，研究人员一直试图设计能够高效地解决所谓np问题的计算机系统，所述np问题包括np完全问题和np难题问题。np难题问题是针对于大的输入大小无法在合理的时间量内解决的问题。然而，所述np难题问题有时可能达到近似解。对于小的输入大小，可以容易地解决所述np难题问题，但是随着添加更多的变量，所述问题以指数方式增长，从而使得现代计算机无法解决所述问题。因此，许多复杂的问题以分解的方式或使用近似来解决，且最终答案在计算上是高消耗的且不精确。不存在发明人已知的能够解决此类问题的数字系统，因此，在实践中，此类问题经由昂贵的近似和直接推断方法来处理。标准的cmos技术是有限制的，因为其只可以输出给定的初始输入位(inputbit)的答案位(solutionbit)。因此，由标准逻辑门组成的此类电路仅进行连续地操作。技术实现要素：本发明的实施方式包括自组织逻辑门、一组自组织逻辑门以及自组织电路。优选实施方式是存储计算(memcomputing)架构，所述存储计算架构提供与传统逻辑芯片相同的正向逻辑(输入到输出)，并且还提供反向逻辑(输出到输入)。优选方法同时使用正向逻辑和反向逻辑解决复杂问题。我们将正向逻辑和反向逻辑的同时实施方式称为自组织(so)逻辑。使用自组织逻辑加快了求解np问题。当使用正向逻辑解决时需要根据输入长度以指数增长的资源(空间、时间和能量)的np问题可以在使用自组织逻辑解决时仅利用多项式资源来解决。这是通过布尔电路定义np问题的直接结果。本发明的优选实施方式还提供自组织逻辑门和电路仿真器。仿真器可以为代码的形式，所述代码使机器对自组织逻辑门和自组织逻辑电路进行仿真。仿真器对存储计算架构进行仿真，所述存储计算架构提供与传统逻辑芯片相同的正向逻辑(输入到输出)并且还提供反向逻辑(输出到输入)。仿真器可以使用自组织逻辑来解决复杂问题。使用自组织逻辑加快了求解np问题。当使用正向逻辑解决时需要根据输入长度以指数增长的资源的np问题可以在使用自组织逻辑解决时仅利用多项式资源进行解决。附图说明图1a和图1b是分别示出通用存储计算机器(universalmemcomputingmachine，umm)的测试模式和解决模式的示意图；图2是数字存储计算机器(digitalmemcomputingmachine，dmm)的复杂级别的欧拉图；图3a(现有技术)是具有m个输入和n-m个输出的标准n端子逻辑门的图；图3b是本发明的自组织n端子逻辑门(solg)的图，所述n端子逻辑门可以同时使用任何端子作为输入或输出；图4a至图4c分别示出了本发明的solgand(so-and)门的稳定组态、so-and门以及so-and门的不稳定组态；图5是由so-and门的网络形成的自组织逻辑电路(solc)的图；图6a示出了本发明的通用solg，并且图6b示出了通用solg的动态校正模块。图7a和图7b示出了在图5的solc中使用以提供稳定性的压控差动电流生成器。图8示出了图7a和图7b的压控差动电流生成器在加法器solc电路操作中的使用。图9示出了函数的示例；图10是稳定性曲线图的绘图；图11是用于解决6位因子分解问题的包括两位加法器和三位加法器的示例solc电路；以及图12是用于解决3个数、3位子集求和问题的示例优选solc电路；图13a至图13d分别示出了用忆阻器形成的且在每个端子处具有动态校正模块的soand门和soor门，以及需要误差的so-not门，以及校正逻辑。图14a示出了由图13a至图13d的solg形成的示例solc，并且图14b和图14c分别示出了solc的正向模式和反向模式；以及图15示出了可以在一个计算步骤中以所需精确度确定两个尾数的商的示例solc。具体实施方式本发明的实施方式是自组织逻辑门(solg)。solg包括忆阻器设备和动态校正模块的组合，所述动态校正模块配置成在向任何端子施加信号时提供稳定的操作。本发明的solg可以从任何端子接受信号，并且不需要在任何其他端子处不存在信号。如果平衡存在，则端子信号可以重叠，并且门找到平衡(不存在从任何端子流动的电流)。如本文中所使用的，忆阻器设备包括提供忆阻行为的忆阻器或基于晶体管的电路。[l.chua，s.m.kang，memristivedevicesandsystems(忆阻设备及系统)，proc.oftheieee，vol.64，is.2，pg.209(1976)]。优选实施方式包括用传统的半导体制造技术制造的物理电路。另外的优选实施方式包括通过代码仿真以模拟solg和来自solg的电路的虚拟电路。因此，本领域技术人员将理解的是，本发明的虚拟电路实施方式使其自身适合以计算机程序产品的形式实现。因此，将理解的是，本发明的实施方式可包括计算机程序产品，所述计算机程序产品包括存储在非暂时性计算机可读介质上的计算机可执行指令，当执行所述计算机可执行指令时，使得计算机执行根据本发明的方法，或者本发明的实施方式可包括配置成执行此类方法的计算机。可执行指令可包括已经编译成机器可读格式的计算机程序语言指令。非暂时性计算机可读介质例如可包括用于存储数据的磁介质、光学介质、基于信号的介质和/或电路介质。所述指令可全部地或部分地从网络计算机下载。此外，将理解的是，如本文中所使用的术语“计算机”旨在广泛地指代能够读取和执行记录的指令的任何机器。还将理解的是，本发明的方法的结果可显示在一个或多个监视器或显示器上(例如，作为文本、图形、图表、代码等)、打印在合适的介质上、存储在恰当的存储器或存储设备中等。本发明的实施方式是自组织逻辑门和自组织逻辑电路。优选实施方式是提供与传统的逻辑芯片一样的正向逻辑(输入到输出)并且还提供反向逻辑(输出到输入)的存储计算架构。使用so逻辑加快了np问题的求解。在使用正向逻辑解决时需要根据输入长度以指数增长的资源的np问题可以在使用so逻辑解决时仅利用多项式资源进行解决。这是通过布尔电路定义np问题的直接结果。我们最近已经表明，我们称之为通用存储计算机器(umm)的新种类的非图灵机具有与非确定性图灵机相同的计算能力，并且因此，所述通用存储计算机器可以利用多项式资源解决np完全/难题问题。参见，f.l.traversa和m.diventra,“universalmemcomputingmachines”(通用存储计算机器)，ieeetrans.neuralnetw.learn.syst.vol.26is.11pg.2702(2015)。umm是包括交互式存储处理器(memprocessor)的机器，所述交互式存储处理器是在相同的物理位置上使用存储器来既处理信息又存储信息的基本单元。通用存储计算机器的计算能力取决于其内在并行性(即，机器的集体状态(而不是单独的存储处理器)计算)及其信息开销(一种嵌入机器中但是不一定由机器存储的信息)。优选实施方式提供自组织逻辑门(solg)。优选实施方式提供整套逻辑门。本发明的优选solg包括忆阻器和标准晶体管，并且其他的solg包括通过提供忆阻行为形成忆阻器设备的晶体管电路。本发明的solg包括忆阻器、忆阻器的仿真器、配置成提供忆阻行为的标准晶体管。本发明的门能够通过为输入位求解来用作常规的逻辑门，但是重要的是，本发明的门还可以通过固定输出位并找到引起该输出的输入位来可逆地工作。本发明的门将其自身自组织成最终的解。本发明的自组织逻辑电路采用solg来实现标准逻辑电路不能执行的许多操作。虽然不受此理论的束缚并且所述理论对于本发明的门和电路的基本发明性质是不必要的，但是发明人相信，本发明的自组织逻辑门和自组织逻辑电路代表与所有形式的现代电子学领域中使用的标准逻辑门和逻辑电路不同的基本概念。本发明提供诸如and、or、xor、not、nor、nand的所有的逻辑门以及可以通过改变输入来获得输出的作为标准门工作的任何其他逻辑门。然而，本发明的门还提供反向操作，从而能够进行改变输出来获得产生所述输出的输入的操作。具有m个输入和n-m个输出的标准n端子逻辑门遵循以下范例：输入端子接收信号，所述门处理输入并将计算的输出发送到输出端子。本发明的自组织逻辑门可以同时使用任何端子作为输入端子和输出端子，即，信号可以同时在任何端子处进出，从而导致输入信号和输出信号的叠加。根据旨在满足门的逻辑关系的一些规则，所述门根据输入分量动态地改变信号的输出分量。优选solg可以具有稳定组态或不稳定组态，其中，在稳定组态中，端子处的信号组态满足所需的逻辑关系(诸如逻辑and或or关系)，并且信号在时间上保持恒定，在不稳定组态中，端子处的信号不满足任何传统的逻辑关系，所以solg驱动信号的输出分量以最终获得稳定组态。优选实施方式还提供自组织逻辑电路(solc)。一组solg被结合以提供优选solc。自组织逻辑电路的示例由自组织and门的网络形成。外部输入发送到与所要求的计算任务相关的一些节点。自组织电路通过发现满足逻辑命题的稳定组态来组织自身，然后在输出节点处读取解。可以在solg的每个节点处发送外部输入信号，并且可以在solc的其他节点处读取输出。电路的连接与电路所要求的具体计算任务有关。使用的连接拓扑和具体逻辑门不一定是唯一的，并且连接拓扑和具体逻辑门可以从标准布尔逻辑电路理论中推导出来。solc可以在数学上视为称为存储计算机器的非图灵机的子类[f.l.traversa，m.diventra，universalmemcomputingmachines(通用存储计算机器)，ieeetrans.neur.nets.&learn.sys.vol.26is.11pg.2702(2015)doi:10.1109/tnnls.2015.2391182]。然而，根据设计目的，solg和solc可以被视为动态系统[l.perko，differentialequationsanddynamicalsystems(微分方程与动态系统)，springer]。由于任何电子电路可以由动态系统描述，所以这个观点更有用，因此动态系统所需的用以恰当运转的性能直接地反映到电子电路中。在此方面中，solc可以在数学上进行如下限定：给出待解决的问题p，并将问题p映射到布尔电路b中，solc是具有由b限定的拓扑的solg的网络；solc的动态性由具有与p的解有关的平衡点的动态系统描述。一旦solc被馈送输入信号，如果初始状态属于平衡点的吸引盆地，则系统以指数方式快速的收敛到平衡点，然后可以读取问题的解。优选实施方式中的solg由忆阻器设备或忆阻器设备的仿真以及标准晶体管的组合形成。示例包括自组织and门、自组织or门、自组织xor门和自组织not门。逻辑0和逻辑1被编码成solg的端子处的电势。例如，我们可以选择参考电压vc，使得具有电压c的端子被编码为逻辑1，具有电压-vc的端子被编码为逻辑0。可以使用忆阻器实现自组织and门和自组织or门。忆阻器本身可以使用标准cmos技术仿真，或以多种方式直接地构建。自组织门通过在每个端子处添加特定的动态校正模块来完成。动态校正模块由电阻r、非线性电导g(v)＝-(v-vc)(v+vc)以及具有不同极化的两个相同的忆阻器m形成。自组织not是必须满足v1＝-v2且i1＝-i2的两端口电子设备。这可以使用标准微电子组件以多种方式实现。sonot可以包含或不包含忆阻器。一个形式为具有通过逻辑1进行馈送的输出端子的soxor门。solg形成布尔代数的完整基组，因此任何布尔函数可以表达为自组织and门、自组织or门和自组织not门以及任何其他门的组合。本发明的自组织逻辑门能够解决标准计算问题以及利用多项式资源(空间，时间和能量)来解决使用普通布尔逻辑利用指数资源解决的计算问题。逻辑门之间的连接应该配置成使得用作动态校正信号的电流能够提高或降低节点处的电势。作为本发明的自组织逻辑门与自组织逻辑电路的能力的另一示例，用于浮点数除法的标准算法需要几个步骤来进行两个数字的尾数的除法。相比之下，使用本发明的solc使得可以在一个计算步骤中以所需的精确度来确定两个尾数的商。为了说明此问题，我们想进行数字a和b的除法，即，我想求得数字c使得c＝a/b。solc可以实际上实现cb＝a。此种用有限位数的二元表示的实现需要额外的位来用于计算的精确度(计算的精确度的详尽处理可以被论证，并且将由本领域技术人员理解，但是对于理解本逻辑电路的强大优点是必要的)。为了以布尔逻辑实现产品，我们需要照常由逻辑门组成的2位加法器门和3位加法器门。这些自组织逻辑门的广泛的数值模拟示出了所述自组织逻辑门按照期望运行。现在，将参考附图讨论本发明的优选实施方式。附图可包括示意图，根据本领域的一般知识以及以下描述，本领域技术人员将理解所述示意图。为了强调的目的，特征可在附图中进行夸大，并且特征可不成比例。我们与同事的先前工作提供了一种机器，所述机器使用线性数量的存储处理器在一个计算步骤中解决子集求和问题的np完全版本，并且此机器是使用标准电子组件构建的。f.l.traversa、c.ramella、f.bonani和m.diventra，“memcomputingnp-completeproblemsinpolynomialtimeusingpolynomialresourcesandcollectivestates”(使用多项式资源和集体状态在多项式时间内存储计算np完全问题)，scienceadvances，vol.1，no.6，p.e1500031(2015)。该机器是完全模拟的，并且因此不可以在没有噪声控制的情况下容易地扩展到任意数量的存储处理器。本发明提供数字模式umm，所述umm是能够使用仅与输入大小成多项式增长的资源来解决非常复杂的问题的可扩展机器。这些被称为数字存储计算机器(dmm)。为了示出本数字umm的功能性和实用性，将本数字umm应用到示例：素数因子分解以及子集求和问题的np难题版本。然而，本领域技术人员将理解dmm的更广泛的适用性。在限定dmm之前，我们限定待解决的示例问题。本领域技术人员将理解的是，dmm具有更广泛的应用，但是所述示例问题对于证明dmm的实用性和操作性是有用的。紧凑(compactboolean)布尔问题定义ii.1：紧凑布尔问题是可以写为布尔函数的有限系统的语句的集合(但不一定是独立的)。形式上，令f:为布尔函数的系统，并且然后，cb问题需要找到f(y)＝b(其中，)的解(如果所述解存在)。此限定包含计算机科学中的许多重要的问题，诸如非确定性多项式(np)时间问题、线性代数问题等。具体的示例问题包括因子分解以及子集求和问题。直接协议和反向协议我们还限定两种方式(协议)来找到此类问题的答案。第一方式可以通过标准布尔电路在图灵机范例内实现。第二方式可以仅使用dmm实现。定义ii.2：令sβ＝{g1,…,gk}为k个布尔函数gj∶的集合，scfs＝{s1,…,sh}为h个控制流语句的集合，并且cf为指定待估算函数gj∈sβ和待执行语句sj∈scfs的序列的控制流。然后，我们限定用于解决cb问题的直接协议(dp)，其中控制流cf以为初始输入，并给出作为最终输出，使得f(y)＝b。一般来说，dp为图灵机应该执行以解决cb问题的有序指令集(程序)。即使dp不是利用图灵机来找到给出的cb问题的解的唯一方法，所有的其他已知的策略(即使它们可能为更优的)也不会改变图灵机的计算复杂性类别。为此，我们在这里仅考虑dp作为用于解决cb问题的一些通用图灵实现策略。布尔函数通常为不可逆的，并且找到cb问题的解不等于找到向量函数f的零点，因为所述解属于而不属于或尽管如此，我们仍然可以想到可以在特定机器上实现以找到cb问题的解的策略。这意味着所述机器必须专门地设计成只解决此种cb问题。下文提供的具体示例解决了因子分解以及子集求和问题的np难题版本。然后，我们定义：定义ii.3：反向协议(ip)通过将布尔系统f编码成能够接受输入b，并且返回输出y的机器来找到给定的cb问题的解，即，f(y)＝b的解。ip可以被认为是使用专用机器的f的“倒置”。算法布尔问题定义ii.4：算法布尔(ab)问题是由使用布尔函数的控制流和合适的控制流语句在数学上形式化的语句集合所描述的那些问题。cb问题显然是ab问题的子类。然而，难以预先定论ab问题是否可以简化为cb问题。例如，包括仅在满足条件时才终止的循环的控制流不可以总被转换成布尔函数的有限系统f。此外，可以表述为cb或ab的相同的问题在各自的表述中可不具有相同的复杂性。例如，为了将f简化到唯一的布尔系统，如果我们考虑需要估算nβ布尔函数和nc条件分支的控制流cf(即，“if-then”语句为控制流语句的特定情况)，则我们可能需要随着f的维度而增加的资源，f的维度进而随着nc以非多项式增加。我们注意到，通过术语“资源”，我们表示由机器使用来找到特定问题的解的空间、时间和能量。数字存储计算机器dmm存储处理器(具有存储器的处理器)在被施加转换函数δs之后仅具有有限数量的可能状态。转换函数可以使用例如电路或一些其他物理机制来实现，或者可以经由在机器上运行的代码来仿真以形成虚拟电路。重要的特征在于，它们将映射到中，其中n和m为任意整数。a.形式定义我们记得，umm是由一组m个相互连接的存储器单元格(存储处理器)形成的理想机器，其中，m≤∞。这在图1a和图1b中示出，图1a和图1b分别示出了umm的测试模式和解决模式。它的dmm子类执行由控制单元控制的数字(逻辑)操作。存储器内的计算可以通过以下方式进行描绘。当两个或更多存储处理器连接时，通过由控制单元发送的信号，存储处理器根据其初始状态和信号两者来改变存储处理器的内部状态，从而产生内在并行性(交互的存储器单元格在执行计算时同时且共同地改变它们的状态)和功能多态性(根据施加的信号，相同的交互存储器单元格可以计算不同的函数)。[f.l.traversa和m.diventra，“universalmemcomputingmachines”(通用存储计算机器)ieeetrans.neuralnetw.learn.syst.，2015]。定义iii.1：dmm为八元组：不失一般性的，我们将范围限定到因为泛化到任何有限数量的状态是不重要的，并且不会给理论添加任何重大的改变。δ是一组函数。其中，mα是用作函数δα的输入的(由函数δα读取的)存储处理器的数量且mα＜1，并且m′α是用作函数δα的输出的(由函数δα写出的)存储处理器的数量且m′α＜∞；p是选择由δα调用的存储处理器的指针数组pα的集合，并且s为索引α的集合；σ是由计算存储器上的输入设备写入的初始状态的集合；p0是初始指针数组且p0∈p；s0是初始索引α，并且对于一些是最终状态的集合。计算复杂性级别现在，我们使用以上引入的ab问题和cb问题的概念来限定dmm的前两个级别的计算复杂性。本领域技术人员将认识到，当在直接协议中实现时，dmm还可以用作标准图灵机。这意味着能够设计dmm来处理其ab公式化中的问题，并设计其他dmm来处理其紧凑布尔公式化中的问题。定义iii.2：如果对于给定的为了验证y是否满足f(y)＝b，dmm实现f(y)和dmm实现来自问题的ab公式化的cf都需要n的多项式资源，则将cb问题称为dmm的多项式紧凑(pcm)。定义iii.3：如果对于给定的为了验证y是否满足f(y)＝b，dmm实现f(y)需要多于n的多项式资源，而dmm实现来自问题的ab公式化的cf仅需要多项式资源，则将cb问题称为dmm的非多项式紧凑(npcm)。我们还可以基于dp和ip的复杂性来限定其他三个计算复杂性级别。定义iii.4：如果利用dp和ip来找到f(y)＝b的解y均需要n＝dim(y)的多项式资源，则将cb问题称为dmm的多项式可逆(pim)。另一方面，定义iii.5：如果利用dp找到f(y)＝b的解y需要多于n的多项式资源，而利用ip找到f(y)＝b的解y仅需要多项式资源，则将cb问题称为dmm的存储计算多项式可逆(mpim)。相反地，定义iii.6：如果利用dp和ip来找到f(y)＝b的解y均需要多于n＝dim(y)的多项式资源，则将cb问题称为dmm的非多项式可逆(npim)。最后，我们注意到，ip需要多于多项式资源而ip仅需要多项式资源的情况属于npcim，并且反向协议和直接协议两者均需要多于多项式资源的情况属于cb\pcm。然而，两种情况对目前的工作没有意义。因此，在这里我们不定义它们。图2中示出了dmm的复杂度级别的欧拉图。图2是关于数字存储计算机器的计算复杂度级别的欧拉图。在所有的问题中，ab(算法布尔)、子类cb(紧凑布尔)可以在pcm(多项式紧凑)、npcm(非多项式紧凑)、pim(多项式可逆)、mpim(存储计算多项式可逆)、npim(非多项式可逆)时被解决。应注意，npcm＝pim∪mpim∪npim。dmm内的ip的拓扑实现dmm可以设计成实现dp或ip。由于dp的实现与图灵机一样，所以未添加任何新的东西，因此我们仅讨论后一种情况的实现。我们关注以布尔系统f为特征的给定的cb问题。由于f由布尔函数组成，因此我们可以将f映射到由逻辑门组成的布尔电路中。然后，通过将布尔电路映射到存储处理器的连接中，可以在形式上完成将f实现到dmm中。然后，dmm可以以图1a和图1b中所示的两种不同的模式工作(具体地，以测试模式和解决模式工作)。dmm包括多个存储处理器10以及控制单元14。控制单元14将连接拓扑从输入状态映射到输出状态。存储处理器10是两态互连的元件，所述两态互连的元件根据控制单元14馈送的外部信号和通过它们的连接来自另一存储处理器的信号两者来改变所述两态互连的元件的状态。δ是计算中涉及的所有转换函数的组成。图1a示出了用于验证cb问题的给出的解的测试模式，而图1b示出了ip实现的解决模式。在测试模式(图1a)中，控制单元14为适当的存储处理器10馈送信号编码y。以此方式，第一转换函数δα接收它的输入。执行所有转换函数的组合，我们获得输出f(y)，将f(y)与b进行比较以确定y是否是cb问题的解。在此情况下，转换函数表示通过存储处理器的连接拓扑的f的编码。在解决模式(图1b)中，控制单元为适当的存储处理器馈送信号编码b。第一转换函数接收它的输入，并且所有的转换函数的组合产生输出y。转换函数仍表示通过存储处理器的连接拓扑的f的编码。然而，转换函数作为一些系统g工作，使得g(b)＝y。应注意，g在严格意义上不是f的倒转，因为g不可作为布尔系统存在。为此，我们称g为f的逆拓扑，并且将δ-1称为δ的逆转换函数。dmm通过将布尔系统f编码到连接拓扑上来工作。这意味着我们利用由大量存储处理器以及与f和输入长度直接有关的连接拓扑形成的给定的dmm来解决具有给定输入长度的给定问题。此外，我们注意到，实现ip以在dmm中解决cb问题的可能性最终与dmm的内在并行性有关。最后，即使实现此类特定的dmm不是唯一的(可存在解决此类问题的不同类型的存储处理器和拓扑)，然而，dmm仍是设计成解决特定问题的专用机器。相反地，图灵机在解决给定问题的意义上是通用机器，我们不得不提供一组待计算的指令。换句话说，图灵机只可以利用dp来解决问题。此外，值得注意的是，dmm不仅仅是标准神经网络(即使神经网络是dmm的特例)。事实上，人工神经网络无法将问题充分地映射到连通的神经元中。相反地，人工神经网络在某种程度上是需要进行训练以解决给定问题的“通用”机器。dmm将网络训练步骤转移到网络拓扑的选择中。我们还注意到，可以使用本发明的dmm来解决加密方案。可以使用实施ip的dmm来高效地解决诸如因子分解或子集求和问题的np问题。这意味着与rsa相同的标准加密系统或基于单向函数概念的其他加密系统可以由dmm破解。例如，用于摘要(digest)/哈希(hash)的sha(密码哈希函数)未被证明是np，但是在现有技术中，sha为单向函数。dmm还可以高效地解决此类单向函数。优选实施方式还提供超出图灵机范例的新的加密系统。作为指导，我们在这里注意到，dmm的加密系统应该基于属于npim类或npcm类的问题，npim类或npcm类的问题在输入的长度上具有比多项式更缩放的dp和ip。然而，如果所有的pcim问题都可以由采用ip的dmm在多项式时间内解决，则npim问题的类能够是空的。在此情况下，我们将转而关注npcm问题。信息开销(informationoverhead)使用先前部分中给出的定义，我们现在可以在形式上定义概念：信息开销。首先，我们强调此信息不存储在任何存储器单元中。存储的信息是对于图灵机和umm两者均相同的香农(shannon)自信息。替代地，存储的信息表示嵌入到dmm的连接拓扑中的额外的信息。因此，我们具有：定义iii.7：信息开销为比率：其中，和是由转换函数读取和写入的存储处理器的数量，所述转换函数是由互连的存储处理器利用与cb问题有关的连接拓扑形成的dmm的转换函数，而和是由转换函数读取和写入的存储处理器的数量，所述转换函数是由非连接的存储处理器的联合形成的dmm的转换函数。求和在所有用于找到问题的解的转换函数上运行。根据此定义，可以使用ip(上文限定的)。相反地，由于是非连接的存储处理器的转换函数，因此找到解的唯一方法是使用dp。因此，属于mpim类的问题具有大于多项式的信息开销，即，相比dp，拓扑编码或“压缩”更多关于问题的信息。再次值得注意的是，此信息是与问题有关的(即，与f的结构(存储处理器网络的拓扑)有关的)某信息，而不是由机器存储的一些实际数据。最后，由于信息开销的不同的性质，我们已经限定的信息开销无法满足信息度量的标准数学性质。相反，所述信息开销在给定的计算网络中提供拓扑的重要性的实际度量。动态系统描绘为了提供实际的物理路线来实现dmm，我们现在根据动态系统来重新公式化dmm。此公式化对于可访问信息和信息开销的形式定义也将是有用的，并且同时清楚地指出dmm的可扩展性以及与并行图灵机的最常见限定的主要区别。dmm的动态系统公式化我们考虑在(2)中定义的转换函数δα以及pα，p′α∈p是指针数组和此外，我们使用向量描述dmm的状态(即，存储处理器的网络的状态)。因此，是由pα选择的存储处理器的状态的向量。然后，转换函数δα表现为换句话说，δα读取状态并写入新的状态公式(4)指出转换函数δα同时作用在一组存储处理器上(内在并行性)。这些机器的内在并行性是其功能核心的特征。那么，理解内在并行性的机制以及从内在并行性衍生出什么是非常重要的。为了更深入地分析内在并行性，我们限定δα执行转变所需的时间间隔我们可以通过利用动态系统框架在数学上描述期间的动态性[参见l.perko，differentialequationsanddynamicalsystems(微分方程及动态系统)，vol.7.springer,science&businessmedia，3nded.，2001]。在时刻t处，控制单元将信号发送到计算存储器，所述计算存储器的状态由向量x(t)描述。在由控制单元发送的两个信号之间的间隔内的dmm的动态性由流φ描述(流的定义遵循动态系统形式化[参见l.perko，differentialequationsanddynamicalsystems(微分方程及动态系统)，vol.7.springer,science&businessmedia，3nded.，2001])。即，所有的存储处理器在间隔iα中的每个时刻进行交互作用，使得并行图灵机标准计算机器中的并行性可以从两个角度来看：实际的角度和理论的角度。理论方法仍没有得到很好的评估，并且存在不同的努力来为并行图灵机(ptm)给出形式定义。无论如何，ptm往往产生不能够实际上构建的理想机器。因此，我们更关注对并行性的实用方法的描述。我们在这里给出的定义包括并行图灵机的一些类，具体地为细胞自动机和以非指数增长的并行随机存取机器。我们考虑固定数目(或数目最多以多项式增加的)的中央处理单元(cpu)，所述中央处理单元并行地执行一些任务。在此情况下，每个cpu可以使用其自身的存储缓存工作或根据架构来访问共享的储存器。在任何情况下，在实际的并行机器(pm)中，所有的cpu是同步的，每个cpu在时间tpm(cpu系统的同步时钟)中执行任务，并且在时钟周期结束时，所有的cpu共享它们的结果，并继续进行后续任务。我们还可以在动态系统框架内在数学上描述此描绘[参见l.perko，differentialequationsanddynamicalsystems(微分方程及动态系统)，vol.7.springer，science&businessmedia，3nded.，2001]，以指出与存储计算的内在并行性的区别。让我们考虑分别定义ns个cpu的状态和由nk个储存器单元形成的总储存器上写入的符号的状态的向量函数和只要cpu执行其计算，cpu就在每个时钟周期处独立地运行，所以存在描述形式的计算期间的动态性的ns个独立流，其中是由第j个cpu写入的储存器单元。由于第j个cpu仅在时间t处而不在间隔期间读取储存器k(t)，并且除了单元之外，第j个cpu不在其上执行任何改变，ipm期间的整个状态的演变完全由独立方程组(8)确定。与公式5进行的快速比较示出了与存储计算机器的根本差别：在每个间隔中，ns个cpu不以任何方式互动，并且ns个cpu的动态性是独立的。可访问信息现在，让我们考虑分别具有相同数量m个存储处理器和标准处理器并且花费相同的时间t来执行计算步骤的dmm和ptm。此外，我们还可以假设，在时间t和t+t处，计算机器(无论是dmm还是ptm)具有可以是0或是1的储存器单元的状态。因此，dmm和ptm两者的所有可能的初始组态或最终组态的数目均为2m，并且香农自信息对于两者均相等，即is＝-log2[2-m]＝m。定义iv.1：可访问信息ia是机器在计算期间(即，在间隔期间)探测的组态空间的体积。我们注意到，即使可访问信息的概念和定义遵循统计力学的原理，可访问信息的(以及上文给出的信息开销的)概念和定义也不是意义上的标准信息度量，因此所述概念和定义不满足信息度量的通常性质。另一方面，我们的定义能够突出对指出dmm(或一般的umm)与图灵机之间的差异有用的相关特征。信息开销vs.可访问信息我们已经引入[f.l.traversa和m.diventra，“universalmemcomputingmachines”(通用存储计算机器)，ieeetrans.neuralnetw.learn.syst.,2015]中信息开销的概念，并且在上文中对其进行形式化。接下来，我们利用动态系统描绘讨论所述信息开销与可访问信息的关系。如上所述，dmm可以在每个计算步骤访问可按指数增长的组态空间。因此，即使dmm从定义明确的组态开始，在另一定义明确的组态中结束(两个组态均属于)，在计算期间，其集体状态(即，存储处理器网络的状态)仍导致由dmm所允许的所有组态的叠加。我们考虑由机器探测的组态空间的体积与可访问信息之间的单位比例系数。现在，可访问信息总是大于或等于计算步骤中涉及的存储处理器的数目。事实上，我们具有2m≤ia≤2m且(mα+m′a)≤2m≤ia。因此，使用公式(3)，我们具有其中，是由非连接的存储处理器的联合形成的dmm的计算步骤i中的可访问信息。我们还注意到，其中为计算步骤i中涉及的存储处理器的总数目。相反地，由互连的存储处理器形成的dmm的计算步骤j中的可访问信息是现在，我们考虑属于pcm的cb问题，其中n＝dim(y)，并且f为相关的布尔系统。通过以上定义，在计算中(在测试模式或解决模式中)涉及的存储处理器的数目是n的多项式函数。此外，解决mpim中问题的步骤的数目对于ip(即，当互连的存储处理器将f编码到连接拓扑中时)的情况是多项式的，而在dp(例如，非连接的存储处理器的联合)的情况下，解决mpim中问题的步骤的数目能够多于多项式。然后，存在两个正多项式函数p(n)和q(n)，使得我们可以把此关系带入到公式(9)中，并且具有(由于所有的数量都与相同的机器有关，所以我们可以省略上标t)：值得注意的是，关系(10)对于任何类型的拓扑(包括不具有连接的拓扑)均为有效的。事实上，在没有连接和计算步骤涉及到所有的存储处理器(其相当于ptm)的情况下，我们具有：p＝q,并且io≤1，即，没有信息被编码(压缩)到机器的拓扑中。另一限制情况为连接拓扑不与问题有关(与神经网络中相同)。在此情况下，p或q中的至少一个不可以为多项式，但是比率p/q必须多于n的多项式，并且io由n的多项式函数最大化。平衡点和ip。在先前部分中限定的信息开销和可访问信息可以解释为dmm的计算能力的操作度量。然而，表征这些机器的计算能力的另一重要的特征是其相空间(即，x(t)是(不与组态空间混淆)的轨线的n维空间)的组成。事实上，嵌入到dmm中的额外的信息通过将f编码到连接拓扑上来强烈地影响dmm的动态性，并且具体地，影响其全局相位绘图，即，相空间及其区域(如吸引盆地，分界面等)。为了将所有这些概念联系在一起，描述dmm的动态系统应该具有以下性质：x(t)的每个分量xj(t)具有初始条件xj(0)∈x，其中x为相空间并且还为度量空间。对于属于的每个组态，一个或多个平衡点xs∈x可以是相关的，并且系统以指数快速地收敛到这些平衡。稳定的平衡xs∈x与cb问题的解有关。为了一致地将dmm定义为数字机器，dmm的输入和输出(即，测试模式中的y和b或解决模式中的b和y)必须被映射到一组参数p＝{pj}(输入)和平衡(输出)中，使得(编码逻辑0和1)，并且对于与n＝dim(y)和nb＝dim(b)独立的一些cp,cx＞0，且此外，如果我们用表示最大程度γ中的n的多项式函数，则在测试模式中，并且或在解决模式中，并且其中γx和γp独立于nb和n。可存在与问题的一个或多个解无关的、我们一般用xw(t)∈x表示的其他稳定的平衡、周期轨道或奇异吸引子，但是它们的存在或是不相关的或是可以被认为具有适当的初始条件。系统具有紧凑全局渐近稳定的吸引子[j.hale，asymptoticbehaviorofdissipativesystems(耗散系统的渐近行为)，vol.25ofmathematicalsurveysandmonographs(数学调查和专著)，providence，ri，americanmathematicalsociety(美国数学学会)，2dedition2010]，这意味着系统存在吸引整个空间x的紧算子系统从度量不为零的相空间的区域开始以指数快速地收敛到平衡点，并且相空间的区域可以随着系统的大小而至多以多项式减小。此外，收敛时间可以随着输入大小而至多以多项式增加。值得注意的是，如果相空间完全聚集在平衡点的吸引盆地以及可能的周期轨道和奇异吸引子(如果他们存在)的区域中，则满足最后的要求。我们还指出具有全局吸引子的一类系统是耗散动态系统中的一个[j.hale，asymptoticbehaviorofdissipativesystems(耗散系统的渐近行为)，vol.25ofmathematicalsurveysandmonographs(数学调查和专著)，providence，ri，americanmathematicalsociety(美国数学学会)，2dedition2010]。通过“耗散”，我们不一定指的是“被动”：在泛函分析意义上，主动系统也可以是耗散的[j.hale，asymptoticbehaviorofdissipativesystems(耗散系统的渐近行为)，vol.25ofmathematicalsurveysandmonographs(数学调查和专著)，providence，ri，americanmathematicalsociety(美国数学学会)，2dedition2010]。我们提供的满足这些性质的示例具有附加的优点：唯一的平衡点是问题的解。我们还定义：v＝vol(x)为由x上的一些勒贝格(lebesgue)测度限定的v的超体积，为仅包含所有平衡xs的全局吸引子j的紧凑子集，并且为仅包含所有xw(t)的全局吸引子j的紧凑子集。因此，我们具有j＝js∪jw和js∩jw＝0。我们还定义子超体积vs＝vol(xs)，其中为由js吸引的x的子集。类似地，我们具有子超体积vw＝vol(xw)，其中，为由jw吸引的j的子集。通过定义吸引子js和jw，我们具有xs∩xw＝0，并且由于j为全局吸引子，因此v＝vs+vw。(11)使用这些量，我们可以分别将dmm使用ip求出cb的解的概率或dmm未能求出解的概率两者定义为显然，此分析指的是dmm仅在一个步骤中求出cb问题的解y。在此情况下，我们说对于一些当且仅当dmm正常工作。另一方面，我们可以具有需要几个计算步骤来求出解的ip。在此情况下，在每个计算步骤之后，控制单元可以根据xw添加一些额外的输入。因此，我们可以将成功或失败的概率序列定义为如果求解所需的步骤的数目h是使得的n的多项式函数，则我们可以说dmm正常工作，或更准确地说，dmm已经利用n的多项式资源求出mpim中给定的cb问题的解。自组织逻辑门我们已经在上文给出将dmm表示为数学实体的主要定义和性质。在动态系统的理论中，我们已经将动态系统与使用ip执行计算的可能的物理系统进行关联。然后，我们可以做出结论：在存在具有dmm的性质的系统的预先假定中没有数学上的限制。满足数学上限定的dmm的所有要求的物理系统现在以可以装配在电路中的新型逻辑门的形式提供。图3a示出了传统的逻辑门。所述门包括接收输入信号的输入端子，所述门处理输入，并最终将计算结果发送到输出端子。这是限于顺序操作的顺序逻辑门。图3b提供了本发明的自组织逻辑门(solg)20。solg20包括第一组输入/输出端子22和第二组输入/输出端子24。solg逻辑门20改为提供诸如and、or、xor、not、nor、nand以及任何其他逻辑函数的所有逻辑函数，使得solg逻辑门20作为通过改变输入(在第一输入/输出门22处)来获得输出(在第二输入/输出门24处)的标准门工作，同时solg逻辑门20还通过改变输出来进行“反向”操作，solg逻辑门20动态地提供与该输出一致的输入。通常，这些门是具有允许它们被指定为自组织逻辑门(solg)的性质的对象。solg20可以同时使用来自第一组22和第二组24的任何端子来作为输入/输出，即，信号可以在任何端子处同时进出，从而导致输入信号和输出信号的叠加。根据旨在满足门的逻辑关系的一些规则，所述门根据输入分量来动态地改变信号的输出分量。图4a至图4c示出了示例自组织and门可以具有稳定组态(左边面板)或不稳定组态(右边面板)。在前一种情况下，端子处的信号的组态满足所需的逻辑关系(在图4b的情况下，逻辑and关系)，并且信号将随后及时地保持恒定。相反地，如果给定时间处的信号不满足逻辑关系，则我们具有不稳定组态：solg驱动信号的输出分量以最终获得稳定组态。下面的表1提供solg的状态，所述solg具有作为第一组22的两个端子和作为第二组24的一个端子。在向端子22施加两个输入时，设置对应于and、or和xor的三个单独的逻辑函数来获得端子24处的相对应的普通函数。表1还表示了实现solg操作所必需的状态。表1通用so门参数soandsoorsoxor电路是通过结合solg门形成的。图5示出了由so-and门32的网络形成的自组织逻辑电路(solc)30。在电路30内的solg的每个节点34处，可以提供外部输入信号，并且可以在solc的其他节点处读取输出。外部输入被发送到与当前的计算任务有关的一些节点。自组织电路30通过找到满足逻辑命题的稳定组态来组织自身，然后在输出节点(即，对给定问题的解进行编码的节点)处读取解。电路的连接与电路所需的具体计算任务有关。连接拓扑和所使用的具体逻辑门不一定是唯一的，并且可以从标准布尔逻辑电路理论中推导出来，这意味着对于给定的cb问题，将f映射到连接中可以通过使用标准逻辑关系完成。以此方式，solc30代表可以在图1a和图1b的测试模式或解决模式的任一模式中工作的dmm。基于电子的solg的示例可以使用可用的电子设备在实际中实现solg。图6a示出了通用so门40，so门40通过改变内部参数可以作为soand门、soor门、soxor门工作。因为使用and和xor、或or和xor，所以so门是通用的，因此我们具有完整的布尔基集。图6a的通用门40在第一组输入/输出端子42和第二组输入/输出端子44(在此示例中为一个)处提供编码成电势v1、v2和vo的逻辑0和1。例如，我们可以选择参考电压vc使得具有电压vc的端子编码逻辑1，并且具有电压-vc的端子编码逻辑0。基本电路元件为电阻器、忆阻器(具有存储器的电阻器)42和压控电压发生器44。门40包括两个忆阻器46和应用到每个端子的动态校正模块48。图6b详细地示出了动态校正模块48。忆阻器46分别具有最小电阻ron和最大电阻roff。忆阻器46由以下关系限定vm(t)＝m(x)im(t)(14)电压驱动(16)电流驱动(17)其中，x表示描述系统的一个或多个内部状态的一个或多个状态变量(从现在开始，为了简单起见，我们假设单个内部变量)；vm和im为跨越忆阻器的电压和电流。函数m是x的单调正函数。示例实施方式使用以下关系：m(x)＝ron(1-x)+roffx，(18)上述关系对于描述某种类型的忆阻器的操作是很好的近似。此模型还包括与忆阻器并联的、表示寄生电容效应的小电容c(公式(15))。fm是vm(im)的单调函数，其中，x∈[0,1]，否则为空。满足的单调条件和零度的任何函数将限定忆阻器。在替代实施方式中，忆阻器在功能上替换为晶体管的恰当组合。压控电压发生器(vcvg)是由电压v1、v2和vo指导的线性电压发生器。输出电压由公式(19)给出vvcvg＝a1v1+a2v2+aovo+dc，(19)并且确定参数a1、a2、ao和dc以满足表i中所报告的每个门(and、or或xor)的一组约束特性。这些约束可以总结为以下方案：如果门连接到网络，并且门组态是正确的，则电流不从任何端子流出(门处于稳定平衡中)。否则，vc/ron级的电流以与端子处的电压的符号相反的符号流动。当我们将这些门连接在一起时，这些简单的要求在网络中引起反馈，从而一次性满足所有的门，因为这些门的正确组态是稳定平衡点。值得注意的是，由于除了电压驱动电压发生器之外的所有元件均为无源元件，因此门的平衡点是稳定的且有吸引力的。对于三个so门，表i给出了满足这些要求的一组参数。最后，我们注意到，表i中的参数不是唯一的，并且参数的选择可以严重地影响网络的动态性。通常，为了保证门的稳定性，参数必须满足公式(28)solc的辅助电路当我们使用图6a和图6b的solg装配图5中的solc时，我们可不总是防止与问题无关的一些稳定解的存在。例如，可以表明，通过表i限定的动态校正模块在一些组态中也承认零电压(即，既不是vc又不是-vc)为稳定值。实际上，如果我们在so-and的输出端子处施加vo＝-vc(意味着，我们在so-and的输出处施加逻辑0)，则可能的稳定解为(v1,v2)＝(0,0)(注意到，唯一可接受的解为(-vc,vc),(vc,-vc)以及(-vc,-vc))。图7a和图7b示出了压控差动电流发生器50和压控差动电流发生器的公式以及其函数fdcg。压控发生器应用在图5的solc中的除了接收输入的端子之外的每个solg端子处。vcdcg50承认v＝vc或v＝-vc是唯一的稳定解。考虑控制vcdcg的简化公式。其中，图7中概述了函数fdcg。如果我们考虑0附近的电压v，则公式(20)可以被线性化并给出其中因此，压控发生器相当于负电感，并且足以使0解不稳定。另一方面，如果我们围绕v＝±vc(期望值)进行线性化，则我们获得其中此情况相当于与大小为±vc的dc电压发生器串联的电感。由于压控发生器连接到由忆阻器和线性电压发生器组成的电路，因此v＝±vc是稳定点。任何其他电压v都会引起电流的增加或减小，并且因此，不存在其他可能的稳定点。图8示出了在提供so三位加法器的solc中的vcdcg50的应用。每个没有施加输入的门端子连接到vcdcg50，而那些施加输入的门端子不连接到vcdcg50。加法器的输入是具有电压和的dc发生器。电路进行自组织以使v1、v2和v3与和一致。solc的稳定性分析solc是渐近平滑、耗散的，并且因此，solc具有全局吸引子。所有可能的稳定平衡均与cb问题的解有关，并且所有轨迹均与初始条件无关地以指数快速收敛到平衡。此收敛速率最多以多项式取决于solc的大小。solc动态性由标准电路公式进行描述。使用修改的节点分析，已经表明标准电路公式形成微分代数系统(das)。然而，从理论观点来看，处理常微分方程(ode)通常更简单，因为它允许我们将泛函分析的几个结果应用到动态系统理论。毫无疑问的是，我们获得的ode的结果还应用到ode所源自的特定das。为此，我们首先执行我们系统的降阶，并且在降低线性部分之后，我们获得ode。这样做时，我们需要描述我们的ode的变量仅为跨越忆阻器的电压(nm是忆阻器的数目)、忆阻器的内部变量流入vcdcg的电流(ndcg为vcgcg的数目)以及vcdcg的内部变量公式可以在形式上写为：其中，为线性算子在简写形式中，它读为其中，x≡{vm,x,idcg,s}，并且f可以从公式(21)至公式(24)的右手侧(r.h.s.)读取。我们分别讨论它们中的每一个，并且我们在以下部分中给出所有参数与函数的定义。公式(21)在公式(21)中，c为忆阻器的寄生电容，av,和是从电路方程降低到ode格式得出的常数矩阵[k.eshraghian，o.kavehei，k.-r.cho，j.chappell，a.iqbal，s.al，sarawi和d.abbott，“memristivedevicefundamentalsandmodelingapplicationstocircuitsandsystemssimulation”(应用到电路和系统模拟的忆阻设备基础和建模)，proceedingsoftheieee，vol.100，no.6，pp.1991-2007，2012]。最后，向量函数g∶是通过忆阻器的电导向量的分量限定为公式(26)的忆阻器的电导向量(与公式(18)相比较)gj(x)＝(r1xj+ron)-1，(26)其中，r1＝roff-ron。我们仅考虑限制到的变量x。在此情况下，由于r1,ron＞0，因此g:属于整个域中的c∞。常数向量b是电压发生器50的dc分量的线性变换。因此，我们具有以下命题：命题vi.1：限定在上的公式(21)的右手侧(r.h.s)上的向量函数(27)属于c∞(x)。此外，由于不具有vcdgcg(即，idcg＝0)的系统是无源的，因此矩阵的特征值λj(x)满足(28)。re(λj(x))＜0)其中j＝1,…,n以及公式(22)首先，我们注意到，公式(22)的右手侧上的第j个分量仅取决于变量xj和并且对于j＝1,…,nm，我们可以写出因此，不失一般性的，我们可以讨论取代公式(22)的下标j的公式(29)。公式(29)是电流驱动的忆阻器的公式，其中g(x)vm是通过忆阻器的电流。电压驱动的情况不向我们的讨论添加任何额外的内容，并且对于电压驱动的情况，所有的模型和结果都可以类似地导出。系数α＞0可以与忆阻器的物理相关联[m.diventra和y.v.pershin，“onthephysicalpropertiesofmemristive，memcapacitiveandmeminductivesystems”(关于忆阻系统、忆容系统以及忆导系统的物理特性)，nanotechnology(纳米技术)，vol24.p255201，2013]。电导g(x)由(26)给出。h(x,vm)＝θ(x)θ(vm)+θ(1-x)θ(-vm)，(30)其中，θ为单位阶跃函数(heavisidestepfunciton)。然而，此函数不属于变量x和vm的任何连续性类别(与大多数替代模型相同)。然后，我们以物理上一致且使此函数属于一些连续性类别的方式改变此函数。为此，我们可以写出在给出函数的完整的描述之前，我们在此刻仅需要使用(31)和(32)，并且对于k＞＞1(这是物理上一致的限制)，函数-αh(x,vm)g(x)vm可以利用以下方式在x＝0和x＝1附近进行线性化。根据这些表达式并且使用公式(29)，可以评估0或1周围的x(t)的行为，并且我们具有这证明了以下命题：命题vi.2：使用(31)来表示h(x,vm)，则h(x,vm)∈c∞(x)，并且对于任何且对于任何t＞0，我们具有仅受限于变量x的动态系统(25)的流然后，是在下的的变量子集。此外，边界点0和1是极限点，并且对于的任何开球(openball)，我们具有是开球。在物理上说，由于x应该被限制到因此，此命题允许我们通过使用函数h(x,vm)∈c∞(x)来以自然的方式将x的值限制到现在，我们讨论满足条件(32)以及下一部分的其他有用条件的的实际表达式。目的是找到满足以下条件的1)满足(32)，2)对于任何y≤0，3)对于任何y≥0，4)对于一些r≥0并且对于l＝1,…,r，导数容易证明的是，条件2至条件4通过(37)被满足。其中，系数ai(其中，i＝r+1,…,2r+1)可以通过要求和(其中，l＝1,…,r)来估计。根据条件2至条件4，多项式也是单调的，因为驻点仅位于0和1上(因为条件4)。因此，满足条件2至条件4的多项式还满足(32)。我们还注意到，并且容易示出的是，的缩略积分表达式存在并且表示为作为示例，r＝1、2和3的情况在图9中，图9示出了r＝1(黑实线)、r＝2(虚线)和r＝3(点划线)的函数[公式(37)]的示例，并且在图9中，插图绘制了第一导数、第二导数和第三导数。总之，公式(37)允许我们写出以下命题：命题vi.3：使用(31)来表示h(x,vm)，并且使用(37)来表示然后，对于r的任何特定选择，我们具有限定在处于类cr(x)中的上的(22)的右手侧上的函数：最后，我们使用简短地讨论模型h(x,vm)的令人关注的物理结果。事实上，如果我们考虑我们还可以将vt解释为忆阻器的阈值，因此能够以自然且平滑的方式包括忆阻器公式中的阈值效应。公式(23)在这里，我们具有γ＞0。向量函数fdcg:的每个分量实际上取决于连接有vcgcg的节点处的电压。此电压表示为vm分量(41)的线性组合，其中，和是常数向量。因此，我们可以写出图7中描绘了我们想要利用我们的vcdcg来重现的函数。此形状可以使用几个平滑的阶跃函数(诸如erf、arctan甚至我们在先前部分中定义的θr)来以几种方式获得。因此，我们可以假设至少属于cr(vdcg)。最后，函数ρ还满足ρj(s)＝ρj(sj)＝ρ(sj)，(43)并且函数ρ表达为其中，0＜δs＜＜1。因此，我们具有以下命题：命题vi.4：限定在上的(23)的右手侧上的向量函数(45)至少属于cr(x)。图10提供了公式(24)的稳定图。公式(24)在公式(24)的右手侧上，我们具有函数fs:并且函数fs满足分量方式然后，我们可以将函数fs作为省略下标j的两个变量的标量函数进行讨论。函数fs(idcg,s)为其中，ks、ki、δi、imin、imax＞0并且imin＜imax。注意到，当ki＝0时，公式(47)表示双稳态系统。为了理解变量s的作用，我们注意到，通过仅考虑(47)中s的项，公式(47)表示在s＝0、1处具有两个稳定平衡点并且在处具有不稳定平衡的双稳态系统。现在，我们再次考虑idcg和δi＜＜imin的项。在此情况下，如果至少一个满足则否则上述乘积为1。因此，如果我们考虑则我们具有图10中描述的稳定图，其中，位于ki处的线表示在至少一个满足的情况下的(47)的idcg的项。因此，我们仅具有一个稳定平衡。位于0处的线是至少一个满足并且所有的满足的情况。因此，我们具有两个可能的稳定平衡和一个不稳定平衡。位于-ki处的线是所有的满足的情况。因此，我们仅具有一个稳定平衡。总而言之：如果至少一个则变量s将接近的唯一的稳定点，而如果所有的则变量s将接近的唯一的稳定点。如果至少一个且所有的则s将为或为现在，根据公式(23)和定义(44)，我们得出，如果至少一个则s＜0、ρ(s)＝0且ρ(1-s)＝1，并且简化到是有界的，电流idcg是有界的，并且如果ks＞＞max(|fdcg(vm)|)，则我们具有因此，使用本部分中的分析，我们可以总结出以下命题：命题vi.5：限定在上的(23)的右手侧上的向量函数(49)至少属于cr(x)。此外，存在imax；smax＜∞且smin＞-∞，使得变量s和idcg可以被限制到具体地，smax为f4(s,idcg＝0)的唯一零点。此子集在仅受限于变量idcg和s的动态系统(25)的流下是不变的。此外，边界点是极限点，并且对于任何开放的我们得出是开球。最后的命题可以通过使用(28)来容易地证明。命题vi.6：如果变量且则存在vmax＜∞且vmin＞-∞，使得是在仅受限于变量vm的动态系统(25)的流下的不变子集。全局吸引子的存在考虑由(21)至(24)给出的系统，或(25)中的简写形式。对于我们的动态系统(25)，我们可以在形式上限定半群t(t)，使得或限定我们更熟悉的x(t)＝t(t)x。由于我们已经在先前的部分中证明f(x)∈cr(x)，其中x为完整的紧凑度量空间因此t(t)为cr半群。现在，我们想到，如果对于任何非空、封闭、有界集(其中，)，cr半群是渐近光滑的，则存在紧凑集使得j吸引b。在这里，术语“吸引”在形式上限定为：如果随着t→∞，dist(t(t)c,b)→0，则称集合在t(t)下吸引集合此外，我们得出，如果存在在t(t)下吸引x中的每个点(x的每个紧凑集，x的每个紧凑集的邻居，x的每个有界集)的有界集则称半群t(t)为点耗散(紧凑耗散，局部紧凑耗散，有界耗散)。如果t(t)是紧凑的、局部的、耗散的以及有界耗散的点，则我们简单地称t(t)为耗散的。现在，我们准备好证明以下引理：引理vi.7：限定在(50)中的cr半群t(t)是渐近平滑的。证明：为了证明此引理，我们首先需要将t(t)分解为和的形式：t(t)＝s(t)+u(t)。我们将初始s(t)和u(t)取为其中，kdcg＞0，vo是常数向量，所述常数向量的分量是(41)中的并且是矩阵的伪逆矩阵，矩阵的行是(41)中的向量值得注意的是，对于明确限定的solc，容易示出的是，(逆向，即，通常不成立)我们还执行两个变量移位：s→s-smax(54)由于两个变量仅仅进行移位，因此除了额外的项和smax之外，两个变量在形式上没有改变公式(51)和公式(52)中的任何东西。此外，度量空间相应地改变为了避免增加注释的负担，在下文中，我们将以相同的先前的符号来指代所有的变量和算符，同时牢记(53)和(54)中的变化。现在，通过限定，u(t):并且容易示出的是，u(t)等价于系统。idcg＝0(57)s＝-smax(58)。通过构建，根据公式(28)和(40)中的h(x,vm)的限定，u(t)表示全局无源电路。然后，u(t)是渐近平滑、完全连续的[j.hale，asymptoticbehaviorofdissipativesystems(耗散系统的渐近行为)，vol.25ofmathematicalsurveysandmonographs(数学调查和专著).providence，rhodeisland(罗德岛州普罗维登斯市)：americanmathematicalsociety(美国数学学会)，2nded.，2010]，并且由于u(t)限定在紧凑度量空间x中，因此u(t)是耗散的。现在，遵循[4]的引理3.2.3，我们仅需要证明存在连续函数k:使得随着t→∞，k(t,r)→0，并且如果|x|＜r，则|s(t)x|＜k(t,r)。为了证明此说法，我们首先观察到s(t)等价于系统x＝0(60)由于因此我们得出根据上文给出的fdcg的限定和讨论、变量变化(41)和的定义，我们得出现在，由于我们考虑kdcg，使得kdcgimax＜vc/2，因此根据以上讨论并考虑变量变化(54)，s(t)的唯一稳定平衡点为x＝0，并且该平衡点还是x中的全局吸引子。此外，此平衡是双曲线的，因此存在常数ξ＞0，使得|s(t)x|＜e-ξt。这就做出了证明。引理vi.8：限定在(50)中的cr半群t(t)是耗散的。证明：根据引理vi.7，t(t)是渐近平滑的，因此根据[j.hale，asymptoticbehaviorofdissipativesystems(耗散系统的渐近行为)，vol.25ofmathematicalsurveysandmonographs(数学调查和专著)，ri，americanmathematicalsociety(美国数学学会)，2dedition2010]的推论3.4.3，存在吸引x的紧凑集的紧凑集。还存在吸引x的每个紧凑集的邻居的紧凑集。因此，由于我们的x为有界的，因此引理成立。在此时，我们回想可以例如在hale的文章中发现的并且将对接下来的讨论有用的根据动态系统的拓扑的一些其他定义和结果。对于任何集我们将b的ω极限集ω(b)定义为ω(b)＝∩s≥0cl∪t≥st(t)b。如果对于t≥0，t(t)j＝j，则称集合是不变的。如果半群t(t)中的每个紧凑不变集属于j，则称紧凑不变集j为最大紧凑不变集。如果对于j的任何邻居v，存在j的邻居使得对于t≥0，则不变集j是稳定的。如果存在j的邻居w使得j吸引w的点，则不变集j在局部上吸引点。如果j是稳定的并且在局部上吸引点，则集合j是渐近稳定的(a.s)。如果j是稳定的并且吸引j的邻居，则集合j是一致渐近稳定的(u.a.s)。如果j是吸引每个有界集的最大紧凑不变集，则称不变集j为全局吸引子。具体地，ω(b)是紧凑的且属于j，并且如果j是u.a.s，则j＝∪bω(b)。现在，我们准备证明以下定理：定理vi.9：限定在(50)中的cr半群t(t)拥有u.a.s全局吸引子a。证明：根据引理vi.7和引理vi.8，我们得出t(t)是渐近平滑且耗散的。此外，由于x是有界的，因此有界集的轨道是有界的，并且因此，定理直接地遵循hale的定理3.4.2和3.4.6。平衡点利用先前的引理和定理，我们已经证明，t(t)具有u.a.s全局吸引子。粗略地说，这意味着无论初始条件x(0)∈x的选择如何，t(t)x(0)将渐近地收敛到紧凑有界不变集a。由于在我们的例子中，x为的紧凑子集，因此，a可以仅包含平衡点、周期轨道和奇异吸引子，并且它们均为渐近稳定的。我们首先示出了动态性以指数快速收敛到平衡。然后，我们将讨论周期轨道和奇异吸引子的缺失。根据以上分析得出，对于任何j，平衡必须满足0、vc。此外，导致不稳定平衡，而导致渐近的稳定平衡。然而，如果必要条件且成立，则可以达到这些平衡。为了我们的目的，我们需要idcg＝0。事实上，在平衡处，solc在门节点处具有可以仅为-vc或vc的电压。在如上所述的电压的此种组态中，门可以保持在正确组态或非正确组态中。在前一种情况下，由于动态校正模块，因此电流不从门端子流出，并且所以idcg的对应分量在平衡处必须为0。另一方面，如果门组态是非正确的，则在平衡处，我们具有从门端子流出的vc/ron级的电流。这些电流可以仅由idcg的分量补偿。因此，如果我们用kwrongvc/ron表示当门处于错误组态中时从门端子流出的电流的最小绝对值，则kwrong＝o(1)，并且考虑到vcdcg具有我们得出具有idcg的非零分量的平衡消失，并且仅存在对于idcg＝0的平衡。然后，利用此讨论，我们已经证明了以下定理。定理vi.10：如果条件(64)成立，则对于任何j＝1,···,ndcg，t(t)的u.a.s稳定平衡(如果他们存在)满足sj＝smax(66)此外，这暗示了门关系在相同的时间均被满足。此定理是非常重要的，因为它与以下定理相同。定理vi.11当且仅当在solc中实施的cb问题具有对于给定输入的解，t(t)具有平衡。我们还可以分析平衡以证明平衡的指数收敛性。着眼于此目标，我们首先在平衡处分析公式(22)。在此情况下，对于每个忆阻器，我们可以具有两种可能的情况：其中为流过忆阻器的电流的绝对值，以及为vc/roff的一倍以上的整数(这可以使用表i中的参数并带入满足so门的公式(19)中的v0、v1和v2的值来证明)并且xj＝1。在第二种情况中，我们具有并且xj可以取[0,1]范围中的任何值。后一种情况暗示了对于给定的vm，平衡不是唯一的，但是我们具有平衡的连续统，所述平衡都具有相同的vm、s和idcg，但是不同的x。x的一些分量(与分量vm有关的那些分量等于0)的不确定性在平衡附近产生中心流形。然而，这些中心流形与平衡稳定性无关，因为这些中心流形直接关系到x的分量的不确定性，并且这些分量可以在其整个范围[0,1]内取任何值。因此，我们不得不仅考虑平衡的稳定流形。总之，由于在稳定流形中，cr半群(r≥1)具有指数收敛，并且在我们的情况中，中心流形不影响收敛速度，因此这证明了以下定理。定理vi.12：t(t)的平衡点在其所有的吸引盆地中具有快速的指数收敛。最后，为了检查solc的可扩展性，我们想要研究平衡如何根据solc的大小进行收敛。然后，我们写下围绕平衡点的系统的雅可比行列式(jacobian)。根据定理vi.10中的条件和以上分析，可以表明，在平衡中评估的公式(25)的f(x)的雅克比行列式为：我们还假设，在第二块行中，我们已经消除对于成立的所有方程，并且我们已经从第二块列中消除与不确定性xj有关的所有列。由于我们想要研究的jf的特征值，因此此种消除对于我们的分析是安全的。事实上，我们注意到，与非空特征值有关的特征向量是具有与不确定性xj对应的空分量的向量，因为与非空特征值有关的特征向量与jf的零行有关。我们从(68)可以看出，由于除了最后一个块之外，jf的最后的块列和块行中所有块均为零，因此jf(x＝xs)的特征值仅仅是的特征值和(69)的特征值的联合。现在，由于是与恒等式i成比例的对角矩阵，因此更明确地，其相关的特征值不取决于电路的大小。为了研究的谱，我们注意到，我们具有其中导数是根据平衡点在或-vc中估算的。因此，的特征值是rlc忆阻器网络的时间常数。尽管不容易说明关于一般rlc网络的时间常数的事情，但是在我们的例子中可以做出一些考虑。电容、电感、电阻全部相等(或者如果加入噪声，则电容、电感、电阻彼此非常接近)。此外，网络是有序的，意味着存在非平凡的周期性，并且每个节点的连接数目是有界的并且独立于尺寸。根据这些考虑，我们的网络实际上可以通过其最小单元格(即，重复以形成我们所考虑的整个网络的最小子网络)进行研究。这暗示了网络的较慢的时间常数最多为网络中的单元格的数目乘以单个单元格的时间常数。在这些条件下，我们已经证明了以下定理：定理vi.13：以多项式增长的solc最多支持以多项式增长的时间常数。在上文中，我们已经证明了t(t)具有u.a.s.全局吸引子。我们还提供了证明t(t)在整个稳定流形中的指数收敛的平衡分析，并且讨论了t(t)随着系统的尺寸的收敛速度，从而示出了最多随着系统的尺寸以多项式收敛。因此，为了全面了解在物理上利用solc实现的dmm，应该讨论的最后特征为：全局吸引子的组成。为了分析全局吸引子，我们使用统计方法。我们做出以下假设：1)电容c足够小，使得如果我们干扰网络的节点中的电势，则干扰在时间τcc＜＜τm(α)中传播，其中，τm(α)是忆阻器的切换时间(显然地，τm(α)是逆α的线性函数)。对于我们的系统，时间常数τc与忆阻器和c有关。2)函数fdcg(参见图7)的q足够小，使得时间满足γ-1＜＜τdcg，即，电流idcg达到所花费的时间比其达到所花费的时间小得多。3)忆阻器的切换时间满足γ-1＜＜τm(α)＜＜τdcg。4)x的初始条件在x中随机选取。在继续之前，我们描述我们的solc的特殊行为，其中，所述特殊行为可以通过基尔霍夫电流定律引起的非局域性并且观察dcm如何工作来证明。如果我们在网络“准瞬时”(即，在切换时间τc＜＜τ＜＜τm(α)内)的一点中改变δv级的电势，将存在包括切换点的子网络s，在τc级的时间内，节点处的许多电势将改变相同的δv级。此改变只是网络的rc性质的结果，是在τc时间尺度上存在的唯一分量。在τm(α)级时间之后，子网络s将作为dcm的结果而达到稳定组态。因此，对于电路的节点中的干扰δv，在时间τm(α)内存在网络的整个区域s的重新配置。如果在给定的节点j中，电流达到则控制idcg的公式变成didcg＝-γidcg，因此电流在γ-1级的时间内降低到imin。如果我们将imin设置得比网络的特征电流小得多，则在γ-1级的时间内，节点j处的电势将经历ronimax级的电势变化δv(如果imax足够大)。此外，由于τm(α)＜＜τdcg，因此网络在电流再次开始增长之前重新配置区域s。出于这种考虑，并且使用上述条件1至条件4，我们可以对我们的网络做出统计解释。我们考虑足够大的系统，并且由于所述系统是由基本单元格的组合构成的，因此我们假设τc足够小，使得子网络s中节点的密度是均匀的。在x中选取作为初始x(0)的随机点，我们得到，vcdcg的一部分mdcg/ndcg以速率达到imax，并且因此进行切换。这意味着存在一部分节点，所述一部分节点由δv≈kwrongvc/ron以速率踢除。根据我们的上述讨论，如果x-是系统在踢除之前的组态，并且x+是系统在踢除之后的组态(它们的时间距离具有γ-1级)，则我们得出，距离dist(x-,x+)具有限定为infy∈xsupx∈xdist(x,y)的x的半径的级。这意味着，这些踢除将系统置于彼此远离的x的点中。由于我们已经在x中任意地选择初始x(0)，因此踢除将在时间和空间上(即，在网络节点中)随机地发生。这意味着系统探索整个x。值得注意的是，与蒙特卡洛(montocarlo)模拟的情况相同，当我们估计n维积分时[f.rossi，theoryofsemiconductorquantumdevices(半导体量子设备理论)，macroscopicmodelingandsimulationstrategies(宏观建模和模拟策略).berlin：springer–verlag，2016]，在这里，solc以变量数目为线性的方式来探索x，即，solc需要随着系统的维数最多以线性增长的若干踢除。所有此种分析允许我们得出结论：在我们的solc中，周期轨道或奇异吸引子不可以与平衡共存。事实上，周期轨道和/或奇异吸引子(如果它们存在)两者均产生大的solc的电势的波动。由于vcdcg和dcm的组合，这些波动具有vc/ron级，并且不是局部的，而是分布在整个网络中。因此，根据先前的分析，如果周期轨道和/或奇异吸引子存在，则它们应该迫使系统探索整个空间x。然而，如果平衡点存在，则通过探索x，系统将在τdcg级时间内截取仅与系统的大小、x的稳定流形成线性增长且在平衡点崩溃的数目。因此，全局吸引子仅由平衡点形成或仅由周期轨道和/或奇异吸引子形成。i.多项式能量消耗我们最后注意到，solc随着输入大小以多项式增长，每个门中的每个节点只可以支持有限的电压(由电容c截止)并且在平衡处，所述电压不取决于系统的大小。电流也是有限的，并且电流的界限与solc的大小无关。解在有限时间内得到，所述有限时间在多项式上取决于solc的大小。因此，能量消耗只可以随着solc大小以多项式增长。这还可以按照以下更数学的方式看待。度量空间是有界的紧凑空间且其范围的支持不取决于solc大小，因此，能量消耗仅可以随着solc大小以多项式增长。现在，我们通过解决两个不同的np问题(一个np难题问题)来提供所有这些陈述的数值证明。利用dmm的vnp问题的解素数因子分解让我们考虑整数n＝pq，其中p和q是两个素数。此外，我们定义p、q和n的两元系数pj、qj和nj，使得并且对于q和n是类似的。因此，np、nq和nn分别是p、q和n的位的数目。np问题在于找到两个唯一的素数p和q，使得n＝pq。从f(y)＝b开始，我们可以构建如图11中所示的solc60(nn＝6)。solc的输入是由nj表示的发生器。这些发生器根据nj的逻辑值施加电压vc或-vc。因此，此类发生器是dmm的控制单元并且对b进行编码。由pj和qj表示的处于相同的电势处的线是我们问题的输出，即，它们通过电压对系数pj和qj(即，y)进行编码。因此，为了读取solc的输出，测量这些线处的电势就足够了。值得注意的是，一旦门具有自组织，所有线处的电势的值就将为vc或-vc。因此，在读取输出时不存在精度问题，从而意味着电路的鲁棒性和可扩展性。可扩展性分析—图11示出了用于解决6位因子问题的优选solc。使用标准逻辑门可以容易地设计所述电路来计算两个整数的乘积，然后由solg代替标准逻辑门。所述电路由以上描述的solg组成。具体地，solg为soand60、soxor62和soor64。图11中的电路可以构建成任何大小的b，并且solg的数目按照n2进行增长，所以solg与输入成平方地进行缩放。根据以上分析，此solc的平衡是因子分解问题的解，并且所述平衡可以最多在nn的多项式的时间内在指数上达到。最后，由于此电路的能量线性地取决于电路找到平衡所花费的时间和门的数目，因此能量也是有界的。因此，我们得到结论，如果在硬件中实现，则此类电路仍将以多项式资源解决因子分解。另一方面，为了模拟此电路(即，求解ode(25))，我们需要有界的小时间增量dt，所述小时间增量dt与电路的大小无关，并且仅取决于可以与以上讨论的时间标度相关联的最快时间常数。值得注意的是，如果n已经是素数，或用于构建solc的np或nq中的至少一个小于用于解决因子分解问题的p或q的实际长度，则所述问题在此solc内没有解。通过简单地选择np＝nn-1以及(或者反过来)，总是可以避免后一种情况，其中，代表向下舍入算符，即，它将参数朝向负无穷舍入到最接近的整数。此选择还保证了如果p和q是素数，则解是唯一的，并且避免n＝n×1的平凡解。表ii模拟参数参数值参数值参数值ron10-2roff1vc1α60c10-9k∞vt0γ60q10m0-400m1400imin10-8imax20ki10-7ks10-7δs0δi0我们已经将电路实现成电路仿真器。为了简单起见，我们已经将具有np＝nq的solc实施为最多nn＝np+nq的长度。在此情况下，由于对称性，因此可能的解为两个。数值模拟--所述模拟通过从忆阻器内部变量x的随机组态开始并且逐渐地接通发生器来执行。尽管不是必须的，但是我们使用发生器的切换时间，所述时间是nn的二次方程。我们选择vc＝1。在瞬态过后，所有的端子都接近±vc，所述端子在逻辑上为0和1。当由于dcm，所有的端子收敛到±vc时，所述端子一定满足所有的门关系，然后solc求出解。在https：//arxiv.org/pdf/1512.050641512.05064处并且名为“polynomial-timesolutionofprimefactorizationandnphardproblemswithdigitalmemcomputingmachines”(利用数字存储计算机器的素数因子分解问题和np困难问题的多项式时间解)(april22，2016)的有关本发明的出版物中提供了绘图(图12和图13)。我们已经使用72-cpu簇进行了数百次模拟，并且还没有发现solc不收敛到平衡的单个情况。还值得注意的是，我们处理的较大情况(18位的情况)需要模拟具有大约11,000个独立动态变量(即，vm、x、idcg和s)的动态系统。因此，我们正处理巨大的相空间，但是除了平衡外，我们还没有找到任何其他事物。显然，这并不能证明所有可能的尺寸均没有奇异吸引子或极限循环，但是至少对于我们所使用的参数(参见表ii)是这样的。子集求和问题。我们现在示出如何利用多项式资源在solc内解决子集求和问题(ssp)的np难题版本，所述子集求和问题(ssp)的np难题版本是复杂性理论[m.r.garey和d.s.johnson，computersandintractability；aguidetothetheoryofnp-completeness(计算机和难解性；np完全性理论指南)。newyork(纽约)，ny，usa：w.h.freeman&co.,1990]中最重要的问题中可论证的一个。问题定义如下：如果我们考虑基数n的有限集则我们想要知道是否存在非空子集其和是给出的数字s(np完全版本)。此外，我们将设法寻找解决问题(np难题版本)的至少一个子集(如果其存在)。ssp的复杂性按照其基数(n)以及用于表示g的任何元素的位的最小数目(即，精度p)两者来表述。当n和p具有相同阶数时，问题变得难以解决，因为已知的求解所述问题的算法为n的指数或p的指数。在这里，我们考虑ssp的np难题版本，在ssp的np难题版本中，g的所有元素均为正数。它们不可以同样在solc中实施的情况需要稍微复杂的拓扑，并且将在别处发表。为了解决ssp，我们试图找到cj∈z2的集合，使得∑jcjqj＝s(70)其中，qj∈g并且j＝1,···,n。因此，我们的未知数是cj，其中y是cj的集合。公式(70)可以容易地通过布尔系统f(y)＝b以布尔形式表示，其中，b由s的二元系数组成，所述s填充有大量零，使得dim(b)与用于表示∑jqj的二元系数的最小数目p相等。容易证明的是，dim(b)≤log2(n-1)+p。此布尔系统可以在如图12所示的solc中实现。图12示出了用于解决3个数字、3位的子集求和问题的示例solc。可以使用标准逻辑门来设计所述示例solc以计算每个乘以未知位的整数的和，然后使用solg来代替标准逻辑门。所述电路由以上描述的solg组成。具体地为soand60、soxor62和soor64。在这里，控制单元由实现s的二元系数的发生器组成，并且输出可以通过测量由图12中的cj指出的线处的电压来读取。可扩展性分析--此电路在p中线性地增长，并且在n中以n+log2(n-1)增长。最后一项是由于在(70)中求和期间的连续余数引起的。这由图12中的solc的左边的额外加法器表示。同样在此情况下，与因子分解相同，我们得出具有与p和q成多项式增长的solc，所以ssp属于mpim类，从而表明，与图灵机范例不同，因子分解和子集求和问题在存储计算范例内共享相同的复杂性。数值模拟--我们已经以类似于因子分解的方法来执行solc的模拟。与因子分解的情况一样，当所有的门电压均为1或-1(逻辑上分别为1和0)时，求出解。我们同样对此情况执行了广泛的分析，并且从随机初始条件开始直到n＝9并且p＝9都未找到周期轨道或奇异吸引子。最后，同样对于子集求和问题，如果不存在解，则系统将不会收敛到任何平衡。关于np＝p问题的讨论用于模拟dmm(并且具体地为solc)的资源可以以cpu模拟它们的浮点运算的数目进行量化。由于我们实际上是对ode(公式(25))进行积分，因此浮点运算的数目取决于：i)线性的dim(x)(如果我们使用与前向欧拉(forwardeuler)或龙格-库塔(runge-kutta)相同的正向积分方法[j.stoer和r.bulirsch，introductiontonumericalanalysis(数值分析入门)springerverlag，2002])或最多二次方的dim(x)(如果我们使用与后向欧拉(backwardeuler)或梯形法则(trapezoidalrule)相同的后向方法[id])，以及ii)取决于我们用于对模拟总周期进行积分的最小时间增量，或者换句话说，线性地取决于时间步长nt的数目。我们分别讨论它们。在上文中，我们已经看到，对于np问题，我们得出，dim(x)在问题的输入中以多项式缩放(对于因子分解，以位的数目的平方缩放，对于ssp，在集合g的精度和基数两者中线性地缩放)。还注意到，我们通过将np问题映射到更一般的np完全问题、布尔可满足性问题(sat)中来解决这些np问题，然后我们通过直接地编码表示特定问题的sat(此sat是紧凑布尔形式的，我们用f(y)＝b表示)来构建solc。这意味着dim(x)线性地依赖于用于表示sat的基本逻辑门(即，and、or、xor)的数目。用于执行模拟的时间步长的数目nt具有双边界。第一边界取决于最小时间增量δt，并且第二边界取决于模拟的最小周期ts。前者取决于solc的最小时间常数。最终，此时间常数不取决于电路的大小，而取决于我们模拟的单个设备的性质。另一方面，ts可以取决于系统的大小。事实上，ts是我们需要清楚地找到系统的平衡的最小时间。因此，ts与系统的最大时间常数有关。然而，在上文示出的是，ts最多随着问题的大小而以多项式增长。根据这一切，人们可以推断的是，我们可以使用图灵机来以多项式地模拟dmm，从而促使np＝p。本机器可以用具有存储器的电路元件(诸如忆阻器)和/或标准mos工艺来制造。因为所述机器本质上是经典的对象，所以它们不需要低温温度或维持量子相干性来工作，并且所述机器将整数映射到整数中。因此，所述机器与在冯诺依曼结构(vonneumannarchitecture)内实现的目前的数字图灵机一样具有相当强的抗噪声能力。忆阻器solg门在优选实施方式中，solg忆阻器设备是使用忆阻器实现的。图13a至图13d分别示出了利用忆阻器70、每个端子处的动态校正模块72形成的soand门或soor门、sonot门以及所需的动态校正逻辑。忆阻器70可以使用标准cmos技术进行仿真或经由传统技术进行制造。动态校正模块由电阻r、非线性电导g(v)＝-(v-c)(v+c)、以及具有不同极化的两个相同的忆阻器m形成。电阻r、非线性电导g以及忆阻器m中的每个连接到具有线性驱动函数l1、l2、l3、l4的电压驱动电压发生器。如下面的表中所限定的，线性函数不是唯一的。动态校正模块72利用具有线性驱动函数l1、l2、l3、l4的电压驱动电压发生器实现。线性函数不是唯一的，并且可以被选择以满足以下关系，例如：其中，ie＝vc/ron是当施加电压vc并且忆阻器切换到ron时的在忆阻器中流动的电流。电压与电流之间的前四种关系(前四行)是保证自组织门的正确组态稳定(电流不从端子流出，并且没有试图改变逻辑门的状态的信号)的关系。另一方面，后四种关系(后四行)保证将逻辑门驱动到一些稳定组态的电流。图13c的sonot是必须满足v1＝-v2和i1＝-i2的双端口电子设备。这可以使用标准微电子组件以多种方式构建。sonot可包括忆阻器，或不取决于设计。sonot的一个形式为具有由逻辑1馈送的输出端子的soxor门。图14a示出了由图13a至图13d的solg形成的示例solc。逻辑门之间的连接应该配置成使得用作动态校正信号的电流能够在节点处升高或降低电势。这可以通过在soand门82、soxor门84以及sonot门86的连接中的每个节点处设置小电容80(与忆阻器的典型切换时间相比较小)来实现。为了简化说明，未示出动态校正模块。图14a的solc可以在标准模式(即，在如图14b所示的在上端子处放置输入的正向模式中)中或在图14c中所示的反向模式(即，将值施加到输出(下端子)，并且还将输入提供(或不提供)到上端子)中进行操作。在第一情况下，我们约束门，并且图14b和图14c中示出了结果(通过模拟)，而在后一情况下，我们给予门额外的自由度，并且最终结果将取决于初始条件。反向模式可能仅用于本so电路，并且无法用于发明人已知的标准逻辑电路。用于对浮点数进行除法的标准算法需要几个步骤来对两个数字的尾数进行除法。相反，使用本发明的solc使得可以在一个计算步骤中以所需精确度确定两个尾数的商。为了说明问题，我们要对数字a和b进行除法，即，我们想找到数字c，使得c＝a/b。利用solc，我们实际上实现cb＝a。此种用有限位数的二元表示的实现需要额外的位来保证计算的精确度(计算的精确度的详尽处理可以被论证，并且将由本领域技术人员理解，但是本领域技术人员不需要理解本逻辑电路的强大优点)。为了在布尔逻辑中实现所述产品，我们照常需要由逻辑门组成的2位求和端口和3位求和端口。以此方式，可以构建图15中的电路。我们已经对这些自组织逻辑门执行了广泛的数值模拟，并且示出了所述自组织逻辑门按照预期运行。虽然示出和描述了本发明的具体实施方式，但是应理解的是，其他修改、代替和替换对于本领域的普通技术人员是显而易见的。在不背离应该由所附权利要求确定的本发明的精神和范围的情况下，可以做出此类修改、代替和替换。所附权利要求中阐述了本发明的多种特征。当前第1页12