无人机载光电稳定转台惯性态建模仿真方法与流程

本发明涉及建模仿真方法领域，具体是一种无人机载光电稳定转台惯性态建模仿真方法。

背景技术：

无人机载光电稳定转台(简称光电转台)为可见光摄像机、前视红外仪、激光测距仪、激光指示器、光学稳定瞄准装备的承载机构，具有隔离无人机角运动对承载设备影响、实现姿态自适应控制功能的高技术精密装备。无人机部队官兵在装备飞行训练过程中发现，光电转台执行侦察任务过程中，由于天气能见度、无人机较高航高等因素的影响，操作过程非常复杂，操作手的技术熟练度要求高，对实装飞行过程的依赖度较高。无人机飞行空域较宽，空域协调较为复杂，无人机部队开展实装飞行的条件受到诸多因素的限制。无人机装备的使用寿命有限，不允许频繁地开展实装飞行训练。因此，迫切需要基于三维视景仿真技术的替代训练设备，来解决无人机部队视频侦察的替代训练难题。光电转台工作模式有多种，而惯性态为其它重要工作模式的前提和基础，光电转台不执行惯性态，就不能执行其它几种与执行任务相关的重要工作模式。国内外没有针对无人机载光电转台硬件设备三维视景仿真应用的全数字仿真建模相关研究。

技术实现要素：

本发明的目的是提供一种无人机载光电稳定转台惯性态建模仿真方法，以解决现有技术没有无人机载光电转台仿真建模方法的问题。

为了达到上述目的，本发明所采用的技术方案为：

无人机载光电稳定转台惯性态建模仿真方法，其特征在于：包括以下步骤：

(1)、光电转台抽象化功能构模：

从功能上将光电稳定转台简化为二轴二框架结构，该二轴二框架结构由内环组件、外环组件和支座组成，内环组件安装视点，视点的虚拟光轴线记为模型视轴线，内环组件旋转轴安装在外环组件上，可随外环组件一起运动，内环组件绕旋转轴相对外环组件转动，其转动角为高低角，记为模型高低角，外环组件的旋转轴固定在支座上，可绕外环轴相对于支座做方位旋转，其转动角为方位角，记为模型方位角，支座为安装固定装置，可固定于无人机等运动或静止平台上；

(2)、视轴线惯性稳定递推迭代算法设计：

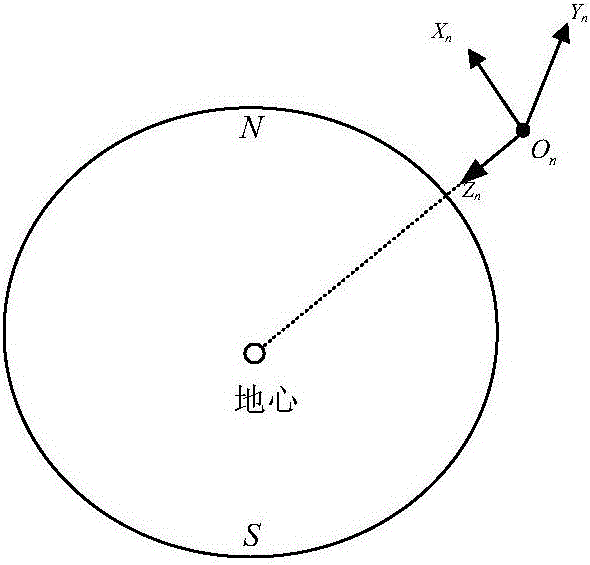
(2.1)、确定无人机N系坐标系，其坐标原点设定在无人机的质心上，X_n轴指向地理北，Z_n轴为重力方向，Y_n轴为向东；

确定航迹坐S系坐标系，航迹坐S系坐标原点在无人机质心处，X_s轴与无人机规划航向同向，Z_s轴为重力方向，Y_s轴与X_s轴和Z_s轴为右手定则关系；

确定无人机U系坐标系，无人机U系与无人机机体固联，其坐标原点O_u为无人机的质心，X_u轴为无人机的机头方向，Z_u轴垂直于机身平面并指向下方，Y_u轴与X_u轴和Z_u轴构成右手定则关系，无人机偏航角为无人机U系X_u轴投影在无人机N系X_nO_nY_n平面上的方位角；无人机俯仰角为无人机U系的X_uO_uY_u平面与无人机N系的X_nO_nY_n平面的夹角，向上为正；无人机滚转角为无人机U系的X_uO_uZ_u平面与无人机N系的X_nO_nZ_n平面的夹角，右转为正；

确定光电转台坐标系，光电转台坐标系包括基座B系、方位环A系、高低环F系和横滚环R系；其中基座B系的坐标原点O_b为转轴中心，Z_b轴由镜头指向目标，X_b轴、Y_b轴分别平行于无人机U系的X_u轴、Y_u轴；方位环A系与光电转台的方位环固联，相对基座B系，只能绕Z_b轴旋转，产生光电转台方位角θ_a；高低环F系与高低环固联，Y_f轴沿高低环轴与方位环A系Y_a轴同向，高低环F系，为方位环A系绕Y_a轴旋转高低角θ_f而得到；横滚环R系与横滚环固联，X_r轴沿横滚环轴并与高低环X_f轴同向，横滚环R系，为高低F系，绕X_f轴旋转横滚角θ_r得到；

确定像平面M系坐标系，像平面M系坐标原点O_m为像主点，Z_m轴与光轴平行且指向目标，当光电转台三个姿态角均为零时，像平面M系Y_m轴垂直飞行方向向右，X_m轴垂直于Y_m轴向上，像平面M系的Z坐标为焦距f；

确定摄像机C系坐标轴，摄像机C系坐标原点O_c位于摄像机光心即像主点处，X_c轴平行于像平面M系的X_m轴，Y_c轴平行于像平面M系的Y_m轴，Z_c轴平行于像平面M系的X_m轴；

地面站K系、无人机K系，坐标原点为分别为地面站和无人机质心，X_k轴向东，Y_k轴向北，Z_k轴与重力反向，X_k轴、Y_k轴和Z_k轴为右手定则关系；

令地面目标点在地面站K系坐标为T:[x_t y_t z_t]^T，无人机瞬时位置在地面站K系坐标为U:[x_u y_u z_u]^T，功能模型对目标跟踪的实时姿态角(a,β)，a,β分别为模型方位角和模型高低角，模型视轴线与地面的交点即地主点O的摄像机C系坐标O_c:[0 0 L]^T，其中L为视轴线斜距；

(2.2)、解算模型视轴线的无人机N系方向余弦：

基于坐标变换原理，地主点O由摄像机C系至无人机N系的坐标变换过程如式(5)：

其中，和分别为无人机N系至航迹S系、航迹S系至无人机U系、基座B系至方位环A系、方位环A系至高低环F系的旋转变换矩阵，分别对应于无人机的航向角φ_hx、包括偏航角俯仰角和滚转角的无人机姿态角、包括模型方位角模型高低角的模型姿态角的输入角参量，其表达式如式(5.1)～(5.4)所示：

其中，M_x、M_y、M_z分别绕X轴、Y轴和Z轴的基本旋转矩阵，

则模型视轴线的无人机N系的方位余弦表达式如式(6)：

其中，上式中的x_n、y_n和z_n表达式如下：

则即为当前时刻k的模型视轴线的无人机N系方向余弦；(2.3)、DFP解算模型姿态角：

DFP解算模型姿态角可使得模型视轴线在采样各时刻保持方向不变，具体来说，确保当前模型视轴线方向余弦与前一时刻的视轴线方向余弦相等，当前时刻根据来反向解算模型方位角和模型高低角；

根据视轴线方向余弦的解算过程可知，解算模型方位角和模型高低角为模型视轴线解算逆向过程，为典型的非线性过程，很难直接用解析表达式计算，需要使用数值迭代法求解，其代价函数J(·)如式(7)：

使用DFP拟牛顿数值迭代算法来解算式(7)中的模型姿态角，为了达到快速收敛提高算法的效率目的，将前一时刻的模型视轴线方向余弦赋予当前模型视轴线方向余弦，并把前一时刻解算的模型姿态角作为DFP解算的迭代输入，基于当前无人机姿态角、无人机航向角为已知参量，使用DFP拟牛顿法迭代解算当前时刻的包括模型方位角和模型高低角的模型姿态角。

本发明工作原理：将实装光电转台复杂的机械伺服结构、陀螺仪稳定回路和图像控制仪自适应控制回路，简化为由视点、内环组件、外环组件、支座组成的二自由度功能模型，基于模型视轴线惯性空间保持不变原理，利用前一采样时刻解算的模型视轴线方向余弦和模型姿态角传递为当前时间的迭代解算初值，使用DFP拟牛顿数据值迭代算法来实时解算功能模型的方位角和高低角，实现惯性态仿真算法的设计，解决了在三维视景仿真模拟训练中的光电转台惯性态的数字建模仿真关键技术问题。

本发明构造了光电转台二自由度功能模型，设计实现了视轴线惯性稳定递推迭代算法，很好地解决了三维视景仿真光电转台的功能建模和惯性态算法建模难题，具有很好的工程可用性。

本发明很好了解决三维仿真环下对光电转台惯性态的数字建模仿真问题。软件仿真测试表明，收敛速度快、计算精度高。将模型和算法加载到三维视景仿真场景中测试后，能够很好地实现了对场景视点的控制，与实装光电转台的逼真度高，无论无人机何种运动方式，或者运动到何地，模型视轴线保持惯性空间相对稳定，仿真视场画面保持稳定不晃动，计算机系统资源实时占用率不高，三维画面流畅稳定。

附图说明

图1为抽象化功能模型示意图。

图2为无人机N系图。

图3为航迹S系图。

图4为无人机U系图。

图5为光电转台坐标系图。

图6为像平面M系与摄像机C系图。

图7为视轴线惯性稳定递推迭代算法流程图。

图8为摄像机C系至无人机N系坐标变换过程图。

图9为DFP解算模型姿态角流程图。

图10为功能模型惯性态仿真方位角变化曲线图。

图11为功能模型惯性态仿真高低角变化曲线图。

图12为惯性态截图1。

图13为惯性态截图2。

图14为惯性态截图3。

图15为惯性态截图4。

具体实施方式

光电转台惯性态是无人机执行作战任务时的重要工作模式，主要用于完成隔离无人机角运动对承载的摄像机/红外仪/激光测距仪/激光指示器/光学瞄准器设备的影响，保持视场在惯性空间相对稳定，有利于无人机光电侦察/目标跟踪/武器瞄准等作战使用。本发明着重解决光电转台惯性工作态的数字功能建模问题，不采购光电转台的实物装备，仅使用计算机软件仿真实现光电转台的硬件隔离角运动、惯性空间稳定功能。发明拟要解决的技术问题包括实装光电转台操作层面功能抽象化建模和惯性态仿真算法设计，完成对光电转台惯性态功能的高逼真度仿真实现。光电转台操作层面功能抽象化建模，着重从光电转台任务执行功能层面进行抽象化构模，设计实现同实装完全一致的操作自由度、承载设备安装位置(摄像机/前视红外仪/激光测距仪/激光指示器/光学瞄准装置的视角位置)、设备响应参数、设备安装位置等等。光电转台惯性态软件仿真算法建模，是本发明的核心内容，拟使用智能计算方法和坐标变换算法，解决对光电转台硬件惯性态的功能仿真，在三维仿真软硬件环境下，用以替代光电转台硬件对承载设备的角运动隔离和保持惯性空间稳定的有效仿真难题，解决部队无人机装备的高逼真度替代训练问题。

本发明的技术方案：

本发明主要包括两部分内容，其一是光电转台抽象化功能构模，其二是光电转台惯性态仿真算法实现。

1、光电转台抽象化功能构模：

实装光电转台为两轴四框架结构，由机械伺服机构、陀螺仪稳定机构和图像控制仪自适应控制机构组成，本发明从功能上将其简化为二轴二框架结构(简记为功能模型)。如图1所示，由内环组件、外环组件和支座组成。内环组件安装视点(包括摄像机/前视红外仪/激光测距仪/激光指示器/光学瞄准装置仿真视点，视点的虚拟光轴线简记为模型视轴线)，内环组件旋转轴安装在外环组件上，可随外环组件一起运动。内环组件绕旋转轴相对外环组件转动，其转动角为高低角(简记为模型高低角)。外环组件旋转轴固定在支座上，可绕外环轴相对于支座做方位旋转，其转动角为方位角(简记为模型方位角)。支座为安装固定装置，可固定于无人机等运动或静止平台上。

2、视轴线惯性稳定递推迭代算法设计

视轴线惯性稳定递推迭代算法为本发明的核心内容，主要使用智能计算方法和坐标变换算法来仿真光电转台硬件工作时对其承载设备的视轴线在光电转台惯性空间内保持稳定过程，即保持光电转台搭载的摄像机/前视红外仪/激光指示器/激光测距仪/光学瞄准装置的视轴线在惯性空间内持续不变，构建实装光电转台在惯性态时其陀螺仪稳定机构、机械伺服机构和图像控制仪的自适应控制过程的功能仿真算法，称之为视轴线惯性稳定递推迭代算法。

具体来说，利用视轴线惯性稳定递推迭代算法解算的模型方位角和模型高低角，控制本发明提出的功能模型，以实现对模型视轴线的实时控制，使其在惯性空间保持稳定，隔离无人机平台角运用的影响。视轴线惯性稳定递推迭代算法基本原理：从惯性态起始时刻开始，将前一时刻模型视轴线的方向余弦和模型姿态角作为当前时刻方向余弦和模型姿态角解算初值，使用非线性数值迭代算法解算当前时刻的模型姿态角，实现对功能模型视轴线的自适应控制，以此类推，实现各采样时刻对模型视轴线的精确控制。

本发明视轴线惯性稳定递推迭代算法设计流程如下：

(2.1)、如图2所示，无人机N系，其坐标原点设定在无人机的质心上，X_n轴指向地理北，Z_n轴为重力方向，Y_n轴为向东。

如图3所示，航迹坐S系坐标原点在无人机质心处，X_s轴与无人机规划航向同向，Z_s轴为重力方向，Y_s轴与X_s轴和Z_s轴为右手定则关系。

如图4所示，无人机U系与无人机机体固联，其坐标原点O_u为无人机的质心，X_u轴为无人机的机头方向，Z_u轴垂直于机身平面并指向下方，Y_u轴与X_u轴和Z_u轴构成右手定则关系，无人机偏航角为无人机U系X_u轴投影在无人机N系X_nO_nY_n平面上的方位角；无人机俯仰角为无人机U系的X_uO_uY_u平面与无人机N系的X_nO_nY_n平面的夹角，向上为正；无人机滚转角为无人机U系的X_uO_uZ_u平面与无人机N系的X_nO_nZ_n平面的夹角，右转为正。

如图5所示，光电转台坐标系包括基座B系、方位环A系、高低环F系和横滚环R系；其中基座B系的坐标原点O_b为转轴中心，Z_b轴由镜头指向目标，X_b轴、Y_b轴分别平行于无人机U系的X_u轴、Y_u轴；方位环A系与光电转台的方位环固联，相对基座B系，只能绕Z_b轴旋转，产生光电转台方位角θ_a；高低环F系与高低环固联，Y_f轴沿高低环轴与方位环A系Y_a轴同向，高低环F系，为方位环A系绕Y_a轴旋转高低角θ_f而得到；横滚环R系与横滚环固联，X_r轴沿横滚环轴并与高低环X_f轴同向，横滚环R系，为高低F系，绕X_f轴旋转横滚角θ_r得到。

如图6所示，像平面M系，坐标原点O_m为像主点，Z_m轴与光轴平行且指向目标，当光电转台三个姿态角均为零时，像平面M系Y_m轴垂直飞行方向向右，X_m轴垂直于Y_m轴向上，像平面M系的Z坐标为焦距f。

如图6所示，摄像机C系坐标原点O_c位于摄像机光心即像主点处，X_c轴平行于像平面M系的X_m轴，Y_c轴平行于像平面M系的Y_m轴，Z_c轴平行于像平面M系的X_m轴。

地面站K系、无人机K系，坐标原点为分别为地面站和无人机质心，X_k轴向东，Y_k轴向北，Z_k轴与重力反向，X_k轴、Y_k轴和Z_k轴为右手定则关系。

令地面目标点坐标为T:[x_t y_t z_t]^T(地面站K系)，无人机瞬时位置为U:[x_u y_u z_u]^T(地面站K系)，功能模型对目标跟踪的实时姿态角(α,β)(α,β分别为模型方位角和模型高低角)，模型视轴线与地面的交点(地主点O)的摄像机C系坐标O_c:[0 0 L]^T(L为视轴线斜距)。

(2.2)、本发明提出的视轴线惯性稳定递推迭代算法，计算流程如图7所示，主要包括解算模型视轴线的无人机N系方向余弦和DFP解算模型姿态角二个关键步骤：

(2.2.1)解算模型视轴线的无人机N系方向余弦：

如图8所示，基于坐标变换原理，地主点O由摄像机C系至无人机N系的坐标变换过程如下：

其中，和分别为无人机N系至航迹S系、航迹S系至无人机U系、基座B系至方位环A系、方位环A系至高低环F系的旋转变换矩阵，分别对应于无人机的航向角φ_hx、包括偏航角俯仰角和滚转角的无人机姿态角、包括模型方位角模型高低角的模型姿态角的输入角参量，其表达式如式(5.1)～(5.4)所示：

其中，M_x、M_y、M_z分别绕X轴、Y轴和Z轴的基本旋转矩阵。

则模型视轴线的无人机N系的方位余弦表达式如下：

其中，上式中的x_n、y_n和z_n表达式如下：

则即为当前时刻k的模型视轴线的无人机N系方向余弦。

(2.2.2)、DFP解算模型姿态角：

DFP解算模型姿态角流程如图9所示，使得模型视轴线在采样各时刻保持方向不变，具体来说，确保当前模型视轴线方向余弦与前一时刻的视轴线方向余弦相等，当前时刻根据来反向解算模型方位角和模型高低角。

根据视轴线方向余弦的解算过程可知，解算模型方位角和模型高低角为模型视轴线解算逆向过程，为典型的非线性过程，很难直接用解析表达式计算，需要使用数值迭代法求解，其代价函数J(·)表达式如下：

本发明使用DFP拟牛顿数值迭代算法来解算式(7)中的模型姿态角。为了达到快速收敛提高算法的效率目的，本发明将前一时刻的模型视轴线方向余弦赋予当前模型视轴线方向余弦，并把前一时刻解算的模型姿态角作为DFP解算的迭代输入，基于当前无人机姿态角、无人机航向角为已知参量，使用DFP拟牛顿法迭代解算当前时刻的模型姿态角(模型方位角和模型高低角)。

为了验证本发明提出的光电转台惯性态仿真建模技术的正确性，给定了功能模型的初始姿态，即模型视轴线的指向，模拟无人机绕地面某点做大圆圈飞行(航向角做大幅度变化)，通过给出的视轴线惯性稳定递推迭代算法，来实时解算功能模型的姿态变化，即模型方位角和模型高低角调整变化，使得视轴线始终保持在初始给定的惯性空间方向，实现功能模型隔离无人机角运动功能，并保持惯性空间稳定。

测试具体参数如下：功能模型始姿态角度[40°,10°]，无人机初始姿态角[10°,10°,10°]，无人机初始航向为正北，其它参数不变。模型方位角和模型高低角变化曲线如图10和图11所示。

由图10和图11可知，随着无人机航向角的快速变化(做大圆周运动)，为使得视轴线保持在初始的惯性方向，视轴线惯性稳定递推迭代算法重新解算了模型方向角和模型高低角，可以看出，模型方位角变化较大，呈360度周期性变化，模型高低角在0度和359度间呈非线性变化。结果表明，本发明提出的无人机载光电稳定转台惯性态建模仿真技术理论正确。

将功能模型加载到三维仿真场景，并把视轴线惯性稳定递推迭代算法软件工程化后用于控制该三维场景视角，惯性态测试截图如图12～图15所示，无论无人机做何种运动方式，也无论运动到任何地点，视场视轴线保持相对稳定，画面不抖动不旋转，计算机资源占用率不高，三维画面流畅稳定，不仅说明无人机载光电稳定转台惯性态建模仿真技术理论正确，而且还证明了该技术具有较好的工程可用性。