一种基于AM嵌套抽样算法的地下水模型评价方法与流程

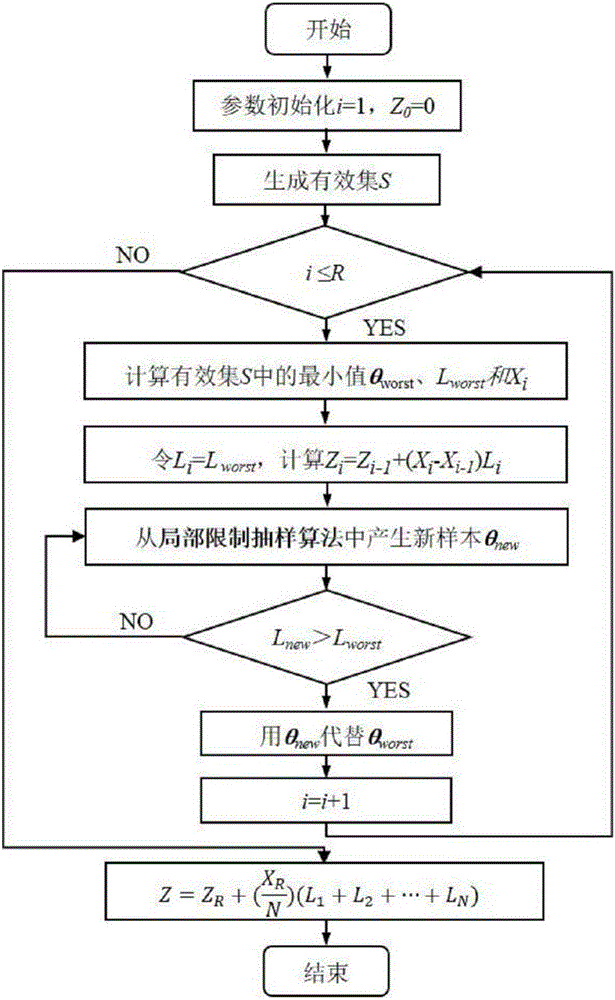
本发明涉及一种地下水模型评价方法，具体涉及一种基于AM嵌套抽样算法的地下水模型评价方法。

背景技术：

近年来，数值模拟技术已成为地下水研究领域中一种不可或缺的方法，对于水资源评价、开发、管理与保护、地下水污染防治等问题具有重要意义。地下水模型的使用不仅可为决策者提供参考依据，也可对未来进行预测和估计。建模方法和工具有很多，基于不同的原理或假设条件，可以建立多个不同的地下水模型。然而，选择不同的模型对预测结果的准确性有较大的影响，因此，如何评价和选择地下水模型是当前需要解决的问题。

边缘似然值(综合似然值、贝叶斯证据)是评价模型表现或计算模型权重的重要依据，然而模型的边缘似然值是其似然函数在复杂空间内的高维积分，直接计算十分困难。计算边缘似然值有多种方法，主要有：①拉普拉斯近似方法；②算数平均方法(AME)；③调和平均方法(HME)等。上述常用方法主要存在以下问题：①拉普拉斯近似方法依赖于边缘似然值的解析形式，不适用于解析形式不存在的情况；②AME在参数先验分布空间内随机抽样，收敛速度慢且得到的边缘概率值偏小；③HME在参数后验分布空间内随机抽样，计算稳定性差且容易高估边缘似然值。

John Skilling(2006)提出了一种计算边缘似然值的新方法：嵌套抽样算法(Nested Sampling Algorithm，NSE)。该方法基于贝叶斯理论，其核心是将复杂的高维积分转化为便于数值计算的一维积分。不同于AME或HME仅在先验或后验概率空间内抽样，也不是简单地将先验与后验空间混合，嵌套抽样法在抽样的过程中由先验空间逐步过渡到后验空间，从而有效降低了从单一分布抽样引起的边缘似然值估计误差。嵌套抽样算法可以看作一种全局优化算法，因为其利用的有效参数集遍历了整个先验分布及后验分布。目前，嵌套抽样方法已经在多个领域得到推广应用，如Elsheikh(2013)等将基于Metropolis-Hasting的嵌套抽样算法(NSE-MH)应用于地下水流模型的评价与不确定性分析，验证了嵌套抽样算法的有效性；Liu(2016)等对NSE-MH中Metropolis-Hasting算法进行改进，分别应用于线性、非线性函数的边缘似然值计算，并与算术平均、调和平均及热力学积分(TIE)方法的计算结果对比，验证了改进后的嵌套抽样算法的计算精度与效率。

嵌套抽样算法(NSE)将复杂的高维积分问题转化为一维积分问题。在具体实施过程中，嵌套抽样算法可以分为嵌套抽样主算法和局部限制抽样子算法(Constrained local sampling)两部分，主算法通过有效集迭代更新的方式实现嵌套抽样，局部限制抽样负责生成每次迭代过程所需的似然值～先验分布累积(L～X)样本。局部限制抽样通常基于概率抽样方法，如Metropolis-Hasting(MH)算法等。

对于常规的基于Metropolis-Hasting算法的嵌套抽样算法(NSE-MH)，该算法原理简单，容易操作，但在应用过程中存在以下问题：①NSE-MH算法的计算效率低，所需的计算量大；②NSE-MH算法的收敛速度慢，在抽样后期MH算法需要多次迭代才能生成满足约束条件(L_i+l＞L_i)的样本；③NSE-MH算法在参数后验分布空间内随机抽样，计算稳定性稳定性较差。因此，上述问题的存在限制了嵌套抽样算法在模型评价中应用和推广。

技术实现要素：

发明目的：本发明的目的在于针对现有技术的不足，提供一种精确、高效的基于AM嵌套抽样算法的地下水模型评价方法。

技术方案：本发明提供了一种基于AM嵌套抽样算法的地下水模型评价方法，包括以下步骤：

(1)根据研究区的水文地质条件，建立一组可行的概念模型M^k(k＝1，2，…，K)来表示实际地下水系统，K表示概念模型的数量，这些概念模型具有不同的结构；

(2)根据研究问题选择一组水文地质参数作为参数向量θ并根据相关监测资料确定其先验概率分布p(θ|M^k)，先验概率分布通常为均匀分布；

(3)从先验分布p(θ|M^k)中随机生成参数向量θ的集合S＝{θ₁，θ₂，…，θ_N}作为有效集，并计算有效集中每个参数向量的联合似然函数L(θ|D，M^k)，；

(4)确定嵌套抽样主算法的迭代次数R，在每次迭代过程中选出有效集S中最差的参数向量作为样本，并根据梯形公式计算边缘似然值的增量ΔZ；

(5)在每次迭代过程中，通过基于AM算法的局部限制抽样从先验分布p中生成新的参数向量θ_new作为候选样本，以替代有效集中最差的样本；

(6)完成R次迭代后，根据有效集S和边缘似然值的增量ΔZ，计算各个概念模型的边缘似然值Z；

(7)根据各个模型M^k(k＝1，2，…，K)的边缘似然值，对各个概念模型进行评价。

进一步，步骤(3)计算联合似然函数L(θ|D，M^k)：

式中，C为协方差矩阵，为单位矩阵I_d，μ为研究区地下水实测数据，Y为根据参数向量θ和模型通过数值模拟得到的数据，μ和Y是与地下水模型相关的状态变量，如地下水水位、地下水中污染物的浓度、温度等，n为实测值和模拟值的个数。

进一步，步骤(4)对于第i(i＝1，…，R)次迭代，计算有效集S中最小的参数向量θ_worst及其对应的似然函数L_worst，令L_i＝L_worst，计算先验分布累积X_i(X_i与有效集中参数向量的个数N和迭代次数i有关)、每一次迭代中的边缘似然值Zi以及边缘似然值的增量ΔZ，其中Z₀＝0，L₀＝0：

进一步，步骤(5)通过局部限制抽样从参数先验分布中生成新参数向量θ_new，若L(θ_new|D，M)＞L_worst，则用θ_new取代原有θ_worst；否则，继续从局部限制抽样算法中生成θ_new，直至满足L(θ_new|D，M)＞L_worst或达到人为定义的抽样次数上限为止。

进一步，步骤(5)基于AM算法的局部限制抽样包括以下步骤：

①从有效集S中随机选择某一参数向量θ作为初始参数向量

②确定AM算法的循环次数H，对于第j(j＝1，…，H)次循环，从正态分布N(C_j)中生成新样本ξ，计算对应的联合似然函数值L_ξ，其中C_j为协方差矩阵；

在T₀次迭代前取固定值C₀，之后自适应更新协方差矩阵计算公式如下：

式中，为已有的所有参数向量的协方差矩阵；

为方便计算，可以通过递归公式计算C_j+1：

式中，s_d＝(2.4)²/d，d是参数的维度，堤一个大于0的常数，I_d是d维单位矩阵，和分别表示前j-1次和j次的抽样的均值；

③若L_ξ＞L_worst，则计算接受概率否则α＝0；

④从均匀分布U(0，1)中生成随机数u，比较u与α的大小；若u≤α则接受否则

⑤重复步骤②-④，直至生成长度为H的马尔可夫链为止；令

进一步，步骤(6)分别计算当前有效集S中的N个参数向量θ₁，θ₂，…，θ_N对应的似然函数L₁，L₂，…，L_N，计算得到边缘似然值z：

有益效果：本发明将嵌套抽样算法中的局部限制抽样算法改进为AM算法，将模型的边缘似然值及后验概率(权重)作为评价地下水模型表现的指标，根据贝叶斯分析理论及嵌套抽样算法，将复杂且不易直接求解的高维积分边缘似然值转化为易于计算的一维积分，在计算地下水模型边缘似然值的案例分析中，本方法通过AM的自适应更新，保证了抽样的质量与精度，与原有的NSE-MH算法相比，在计算结果的计算效率和收敛速度方面有所提高，同时也提高了计算结果的准确性和稳定性。

附图说明

图1为基于AM的嵌套抽样主算法流程图；

图2为研究区平面示意图；

图3为实施例中四个模型M1、M2、M3和M4分别采用三种方法进行地下水流模型抽样过程图。

具体实施方式

下面对本发明技术方案进行详细说明，但是本发明的保护范围不局限于所述实施例。

实施例：如图1所示，一种基于AM嵌套抽样算法的地下水模型评价方法，具体操作如下：

本实施例以三维稳定流地下水流模型为例，研究区如图2所示，为一矩形含水层，东西方向长为5000m，南北方向宽为3000m。含水层的总厚度为60m，从上至下依次为潜水含水层、弱透水层和承压含水层，厚度依次为35m、5m和20m。渗透系数K具有非均质性，渗透系数随机场用各向同性的指数方差模型描述，相关长度为200m，渗透系数K的对数(logK)的方差为1.0。各层渗透系数的平均值依次为1.0m/d、0.1m/d和5.0m/d。此外，含水层水平方向的渗透系数是垂向渗透系数的10倍。

研究区东侧为一河流边界，仅切穿潜水含水层，河水位为35m，河床底板高程为30m，河床水力传导系数为20m²/d；西侧为一定水头边界，水位为56m；右侧有一排水渠，渠道底板高程为45m，渠的水力传导系数为20m²/d。此外，研究区的南部、北部和底部均为隔水边界。潜水含水层接受大气降水的均匀补给，降水量为9.0×10^-4m/d，入渗补给系数为0.15。研究区内共有5口抽水井，总抽水量为1250m³/d(每口井的抽水量均为250m³/d)；区内有32口地下水位监测井(第1层和第3层中各16口)。

考虑到模型结构的不确定性，本次研究采用四个结构不同的概念模型(M1、M2、M3和M4)作为对未知地下水系统的近似。该模型结构的不确定性主要体现为对中间弱透水层的刻画，因为在实际水文地质调查中往往很难查明弱透水层的位置及厚度，而弱透水层又对地下水系统的模拟结果有很大的影响。4个概念模型的空间大小与真实情况完全相同(5000m×3000m×60m)。模型M1假设只有一层潜水含水层；模型M2假设存在潜水含水层和承压含水层，厚度分别为35m和25m；模型M3、M4的结构与真实情况相同，M3中含水层的厚度分别为35m、3m和22m；M4含水层的厚度分别为35m、7m和18m。

本次研究5个水文地质参数，分别为第一层的入渗补给系数、定水头边界水头、河床水力传导系数、第一层的渗透系数随机场的方差和相关长度。其他模型边界条件与真实模型相同。5个参数的先验信息均为均匀分布，其取值范围见表1：

表1地下水流模型中参数的取值范围

定义有效集中样本的个数N＝25，根据公式(1)计算每个样本的边缘似然值L，其中n＝32，μ为地下水监测井中的水位实测值，Y是将样本代入地下水流模型中得到的模拟值。本例中水流模型基于MODFLOW-2005建立并求解。

在本例中，确定嵌套抽样主算法的迭代次数R＝250，在第i(i＝1，…，250)次迭代过程中，选出有效集中的最小的参数向量θ_worst及其对应的似然函数L_worst，令L_i＝L_worst，根据公式(2)计算先验分布累积X_i，根据梯形公式(3)计算边缘似然值的增量ΔZ和每一次迭代中的边缘似然值Z_i。

在第i(i＝1，…，250)次迭代中，通过局部限制抽样(AM算法)从参数先验分布中生成新参数向量θ_new，若L(θ_new|D，M)＞L_worst，则用θ_new取代原有θ_worst；否则，继续从局部限制抽样算法中生成θ_new，直至满足L(θ_new|D，M)＞L_worst或达到人为定义的抽样次数上限为止，本例中设置的抽样次数上限为200。

在基于AM算法的局部限制抽样中，从有效集中随机选择某一参数向量θ作为初始参数向量确定AM算法的循环次数H＝100，对于第j(j＝1，…，100)次循环，从正态分布N(C_j)中生成新样本ξ，根据公式(1)计算对应的联合似然函数值L_ξ，其中C_j为协方差矩阵，在T₀次迭代前取固定值C₀，本例中T₀＝20，C₀为单位矩阵。随后根据公式(4)和(5)自适应更新协方差矩阵；若L_ξ＞L_worst，则计算接受概率α，否则α＝0；从均匀分布U(0，1)中生成随机数u，比较u与α的大小；若u≤α则接受否则直至生成长度为100的马尔可夫链为止；令

完成250次迭代后，根据有效集和边缘似然值的增量ΔZ，计算各个概念模型的边缘似然值Z；分别计算当前有效集中的25个参数向量θ₁，θ₂，…，θ₂₅对应的似然函数L₁，L₂，…，L₂₅，根据公式(6)计算得到边缘似然值Z。

为验证NSE-AM算法的有效性，同时采用算术平均方法(AME)和NSE-MH算法求解。本次案例分析中算术平均方法的样本数量为50万，分别计算4个模型的边缘似然值，作为对应的参考值；NSE-MH的参数取值为：N＝25，R＝250，局部限制抽样算法中生成的马尔可夫链长为100。使用NSE-AM和NSE-MH对4个模型各进行似然值估计10次。由于嵌套抽样算法的各次计算结果不尽相同，本次研究中取10次计算结果的平均值作为最终结果，从而评价嵌套抽样算的综合表现。根据三种方法的迭代过程绘制边缘似然值随抽样次数的变化趋势图，如图3所示；三种方法收敛后计算得到的边缘似然值如表2所示：

表2两种方法计算水流模型的边缘似然值

从中可以得到以下结论：(1)NSE-AM算法的结果准确、计算效率高，AME方法通常需要数十万次的样本数量(即地下水流模型的运行次数)才能达到稳定，需要较长的计算时间，NSE-MH算法也需要5万次以上的模型运行才能收敛，而NSE-AM算法经过大约2万次的模型运行即收敛，且最终得到的结果与AME方法较为接近；(2)NSE-AM算法的适应性好，对于不同的概念模型都能在有限的模型运行次数中达到稳定，而AME方法对于个别与真实情况相差较大的模型，如M1经过50万次模型运行也未达到稳定，而NSE-AM算法在2万次模型运行后基本达到稳定；(3)根据4个模型计算得到的边缘似然值，从小到大的顺序依次为：M1＜M2＜M4＜M3，说明模型M3和M4明显优于模型M1和M2。这表明在考虑相同参数不确定性的情况下，模型的边缘似然值与模型结构概化的合理程度有关，即模型的边缘似然值越大，模型结构概化越合理，概念模型越接近于真实模型。