预测低速冲击下复合材料多层厚板渐进失效的有限元方法与流程

本发明是关于复合材料多层厚板损伤预测领域，特别涉及预测低速冲击下复合材料多层厚板渐进失效的有限元方法。

背景技术：

当前，复合材料多层厚板正广泛应用于航空航天、风力发电、压力容器、汽车等高新技术领域。但是低速冲击损伤对复合材料多层厚板的强度、刚度及使用寿命都有较大的影响，因此必须清楚的了解在低速冲击下复合材料多层厚板的渐进损伤演化过程。

现有的国内外复合材料多层厚板低速冲击研究都是基于二维的平板理论和三维逐层模拟方法。复合材料多层厚板面内跨度与厚度尺寸相对较小，面外影响不可忽略，经典的二维平板理论已经无法适用。然而复合材料多层厚板往往因为层数较多且每层的单元尺寸很小，即使采用三维逐层模拟方法模拟低速冲击载荷下的渐进失效无论是前处理时间还是有限元计算时间都较为庞大。目前能高效且较为准确的预测复合材料多层厚板的低速冲击的方法几乎空白，因此提出一种基于多尺度模型预测低速冲击下复合材料多层厚板的渐进失效的方法尤为重要。

复合材料层合板强度计算分析一般可采用通用的有限元软件ABAQUS进行，但是通过ABAQUS软件自带的模块仅可以基于二维HASHIN失效准则采用逐层模拟方法对复合材料多层厚板进行低速冲击下的渐进失效研究，但无法直接运用较有优势的三维PUCK失效准则，更无法直接采用多尺度模型预测低速冲击下复合材料多层厚板的渐进失效。

技术实现要素：

本发明要解决的技术问题是，克服现有技术中的不足，提供一种预测低速冲击下复合材料多层厚板渐进失效的有限元方法。

为解决上述技术问题，本发明的解决方案是：提供预测低速冲击下复合材料多层厚板渐进失效的有限元方法，包括下述过程：

一、建立含冲锤、复合材料多层厚板以及支撑板的低速冲击有限元模型；

二、建立复合材料多层厚板多尺度模型；

三、利用FORTRAN语言编写的ABAQUS-VUMAT即ABAQUS用户动态材料子程序模块，基于多尺度模型求解低速冲击载荷下应力、应变和损伤；

四、对低速冲击进行计算，进一步获得冲击力、位移、速度和加速度；

所述过程一中，建立含冲锤、复合材料多层厚板以及支撑板的低速冲击有限元模型：基于ABAQUS建立冲锤、复合材料多层厚板、支撑板部件。分别设置材料属性和划分网格，其中复合材料多层厚板在厚度方向网格可根据自身确定的子层压板的个数划分相应的网格，并不需要建立所有单层网格，不同子层压板之间设置ABAQUS自带的双线性内聚力单元。再用ABAQUS-ASSEMBLY模块对其组装之后设置分析步和通用接触属性；

所述过程二具体包括下述步骤：

步骤(1)：基于三维等效理论，建立子层压板的三维等效刚度和应力-应变本构关系：

(a)子层压板的三维等效刚度及其各个分量为：

其中，为子层压板在整体坐标系下的等效刚度矩阵，

为子层压板在整体坐标系下等效刚度矩阵分量，k为子层压板的第k个单层，l为子层压板的第l个单层，n为子层压板的单层总数，V^k为第k个单层厚度占整个子层压板的厚度百分比，V^l为第l个单层厚度占整个子层压板 的厚度百分比，为第k个单层在整体坐标系下的刚度矩阵分量，为第l个单层在整体坐标系下的刚度矩阵分量。

(b)子层压板的应力应变本构关系：

其中，为子层压板在整体坐标系下的等效应力，为子层压板在整体坐标系的等效应变。

步骤(2)：子层压板应力应变分解为子层压板内各个单层的应力应变：

其中，

为子层压板中第k个单层在整体坐标系下的应变分量， 为子层压板在整体坐标系的应变分量，为子层压板中第k个单层在整体坐标系下的应力分量，为子层压板在整体坐标系的应力分量，为第k个单层在整体坐标系下的刚度矩阵分量。

步骤(3)：建立基于应变描述的PUCK失效初始判据和损伤演化准则，具体建立方式为：

(c)对于纤维拉伸和压缩，损伤初始判据为：

其中，和分别为纤维拉伸和压缩的初始失效应变；所述T,C分别指拉伸和压缩；所述ε₁₁是指纤维方向应变；所述分别指纤维拉伸和压缩失效判断因子；

纤维拉伸和压缩的损伤演化准则为：

其中，所述是指纤维拉伸和压缩损伤变量；所述ε₁₁是指纤维方向应变；所述 是指纤维损伤变量达到1的纤维临界拉伸和压缩失效应变；所述是指纤维损伤变量为零的纤维初始拉伸和压缩失效应变；

(d)对于基体拉伸损伤失效初始判据为：

其中，所述指基体拉伸失效判断因子；所述ε₂₂是指基体方向应变；所述是指基体损伤变量为零的基体初始拉伸失效应变；

基体拉伸损伤演化准则为:

其中，为基体损伤变量达到1时基体临界拉伸失效应变；所述是指基体拉伸损伤变量；

(e)对于基体压缩损伤初始判据为：

其中，N是关于失效断裂面的法向方向，T和L是关于失效断裂面的切向方向；Y^C是横向压缩强度，断裂平面上的应力σ_ij(i,j＝L,T,N)由笛卡氏坐标系下的Piola-Kirchhoff应力σ_ij(i,j＝1,2,3)通过旋转矩阵T(α)旋转获得，T(α)为笛卡尔坐标系到断裂面坐标系的旋转矩阵，是断裂面上的横向剪切强度；所述σ_NN是指断裂面的法向应力；σ_NT,σ_NL是指断裂面的切向应力，μ_NL,μ_TN为断裂面面内两个切向方向摩擦系数，θ_f为断裂面的断裂角；所述指基体压缩失效判断因子；所述σ₁₂是指笛卡尔坐标系下面内剪切强度；所述是指在断裂平面内的横向剪切强度；所述σ₁₂₃是指在笛卡尔坐标系下的六个Piola-Kirchhoff应力σ_ij(i,j＝1,2,3)；所述σ_LTN是指在断裂面坐标系下的六个Piola-Kirchhoff应力σ_ij(i,j＝L,T,N)；所述T(α)^T是指T(α)的转置矩阵；所述90°是指采用角度制计量的90度；

基体压缩损伤演化准则为：

其中，所述γ_γ是指断裂面联合剪切应变；和是联合剪切应变的初始和最大应变，γ_NT和γ_NL是断裂面的剪切应变；是指基体压缩损伤变量；

所述过程三具体包括下述步骤：

步骤(4)：通过ABAQUS用户子程序VUMAT实现上述过程，ABAQUS-VUMAT是由应变驱动，随着载荷增加，首先读取各单层的材料信息和铺层信息的参数代码文件，计算各子层压板内各个单层在局部材料坐标系下的刚度矩阵，再转换到整体坐标系下的单层刚度矩阵；

步骤(5)：再通过步骤(1)求取各子层压板的三维等效刚度和子层压板的应力应变；将子层压板的应力应变通过步骤(2)分解为子层压板内各个单层应力应变，并转换为局部材料坐标系下的单层应力应变。再根据步骤(3)判断每个单层是否出现损伤以及求取损伤变量。如果没有出现损伤，则更新应力应变后进入下一个增量步；如果出现损伤，则返回到步骤(4)通过损伤变量更新每个单层在整体坐标系下的刚度矩阵，再通过步骤(1)求取折减后的子层压板的三维等效刚度，计算子层压板三维等效刚度折减系数，并存储为SDV状态变量，更新应力应变后再进入下一个增量步；

所述过程四具体为：将过程一建立的模型主文件和过程三建立的ABAQUS-VUMAT用户子程序联合，使用ABAQUS/EXPLICT显示方法对低速冲击进行计算，进一步获得冲击力、位移、速度和加速度；即完成低速冲击载荷下复合材料多层厚板渐进失效特性的预测。

与现有技术相比，本发明的有益效果是：

本发明利用ABAQUS用户子程序界面的数值实现所建立的基于多尺度模型预测复合材料多层厚板低速冲击下渐进失效的方法，该方法将复合材料多层厚板划分为少量若干子层压板，建立子层压板和该子层压板内每个单层的转化关系，相比于逐层模拟方法，本发明将大大减少复合材料多层厚板在低速冲击下的计算时间，能高效且较为准确的预测复合材料多层厚板在低速冲击载荷下的渐进失效行为。

附图说明

图1为本发明实施例复合材料多层厚板在低速冲击下有限元模型图。

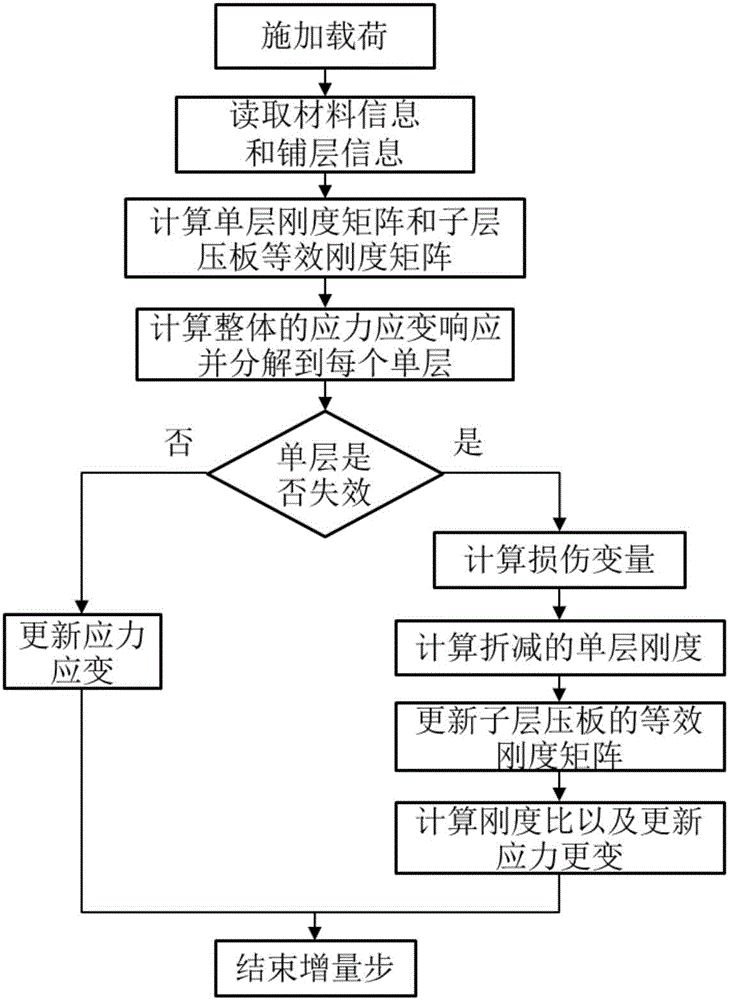
图2为本发明对所提出的基于多尺度模型VUMAT数值实现流程图。

图3为实施例中复合材料多层厚板在25J能量低速冲击下冲击力-时间数值模拟结果与实验结果对比示意图。

图4为实施例中复合材料多层厚板在25J能量低速冲击载荷下冲击力-位移数值模拟结果与实验结果对比示意图。

图5为实施例中复合材料多层厚板在25J能量低速冲击载荷下冲击力-时间数值模拟结果与实验结果对比示意图。

图6为实施例中复合材料多层厚板在25J能量低速冲击载荷下冲击力-位移数值模拟结果与实验结果对比示意图。

具体实施方式

首先需要说明的是，本发明是计算机技术在复合材料多层厚板损伤预测领域的一种应用。在本发明的实现过程中，会涉及到多个软件功能模块的应用。申请人认为，如在仔细阅读申请文件、准确理解本发明的实现原理和发明目的以后，在结合现有公知技术的情况下，本领域技术人员完全可以运用其掌握的软件编程技能实现本发明。凡本发明申请文件提及的均属此范畴，申请人不再一一列举。

本发明中，预测低速冲击下复合材料多层厚板渐进失效的有限元方法，包括下述过程：

一、建立含冲锤、复合材料多层厚板以及支撑板的低速冲击有限元模型；

二、建立复合材料多层厚板多尺度模型；

三、利用FORTRAN语言编写的ABAQUS-VUMAT即ABAQUS用户动态材料子程序模块，基于多尺度模型求解低速冲击载荷下应力、应变和损伤；

四、对低速冲击进行计算，进一步获得冲击力、位移、速度和加速度；

所述过程一中，包括基于ABAQUS建立冲锤、复合材料多层厚板、支撑板部件；分别设置材料属性和划分网格，其中复合材料多层厚板在厚度方向网格根据自身确定的子层压板的个数划分相应的网格，不需要建立所有单层网格，不同子层压板之间设置ABAQUS自带的双线性内聚力单元；再用ABAQUS-ASSEMBLY模块对其组装之后设置分析步和通用接触属性；

所述过程二具体包括下述步骤：

步骤(1)：基于三维等效理论，建立子层压板的三维等效刚度和应力-应变本构关系：

(a)子层压板的三维等效刚度及其各个分量为：

其中，为子层压板在整体坐标系下的等效刚度矩阵，

为子层压板在整体坐标系下等效刚度矩阵分量，k为子层压板的第k个单层，l为子层压板的第l个单层，n为子层压板的单层总数，V^k为第k个单层厚度占整个子层压板的厚度百分比，V^l为第l个单层厚度占整个子层压板的厚度百分比，为第k个单层在整体坐标系下的刚度矩阵分量，为第l个单层在整体坐标系下的刚度矩阵分量；

(b)子层压板的应力应变本构关系：

其中，为子层压板在整体坐标系下的等效应力，为子层压板在整体坐标系的等效应变；

步骤(2)：子层压板应力应变分解为子层压板内各个单层的应力应变：

其中，

为子层压板中第k个单层在整体坐标系下的应变分量， 为子层压板在整体坐标系的应变分量，为子层压板中第k个单层在整体坐标系下的应力分量，为子层压板在整体坐标系的应力分量，为第k个单层在整体坐标系下的刚度矩阵分量；

步骤(3)：建立基于应变描述的PUCK失效初始判据和损伤演化准则，具体建立方式为：

(c)对于纤维拉伸和压缩，损伤初始判据为：

其中，和分别为纤维拉伸和压缩的初始失效应变；所述T,C分别指拉伸和压缩；所述ε₁₁是指纤维方向应变；所述分别指纤维拉伸和压缩失效判断因子；

纤维拉伸和压缩的损伤演化准则为：

其中，所述是指纤维拉伸和压缩损伤变量；所述ε₁₁是指纤维方向应变；所述 是指纤维损伤变量达到1的纤维临界拉伸和压缩失效应变；所述是指纤维损伤变量为零的纤维初始拉伸和压缩失效应变；

(d)对于基体拉伸损伤失效初始判据为：

其中，所述指基体拉伸失效判断因子；所述ε₂₂是指基体方向应变；所述是指基体损伤变量为零的基体初始拉伸失效应变；

基体拉伸损伤演化准则为：

其中，为基体损伤变量达到1时基体临界拉伸失效应变；所述是指基体拉伸损伤变量；

(e)对于基体压缩损伤初始判据为：

其中，N是关于失效断裂面的法向方向，T和L是关于失效断裂面的切向方向；Y^C是横向压缩强度，断裂平面上的应力σ_ij(i,j＝L,T,N)由笛卡氏坐标系下的Piola-Kirchhoff应力σ_ij(i,j＝1,2,3)通过旋转矩阵T(α)旋转获得，T(α)为笛卡尔坐标系到断裂面坐标系的旋转矩阵，是断裂面上的横向剪切强度；所述σ_NN是指断裂面的法向应力；σ_NT,σ_NL是指断裂面的切向应力，μ_NL,μ_TN为断裂面面内两个切向方向摩擦系数，θ_f为断裂面的断裂角；所述指基体压缩失效判断因子；所述σ₁₂是指笛卡尔坐标系下面内剪切强度；所述是指在断裂平面内的横向剪切强度；所述σ₁₂₃是指在笛卡尔坐标系下的六个Piola-Kirchhoff应力σ_ij(i,j＝1,2,3)；所述σ_LTN是指在断裂面坐标系下的六个Piola-Kirchhoff应力σ_ij(i,j＝L,T,N)；所述T(α)^T是指T(α)的转置矩阵；所述90°是指采用角度制计量的90度；

基体压缩损伤演化准则为：

其中，所述γ_γ是指断裂面联合剪切应变；和是联合剪切应变的初始和最大应变，γ_NT和γ_NL是断裂面的剪切应变；是指基体压缩损伤变量；

所述过程三具体包括下述步骤：

步骤(4)：通过ABAQUS用户子程序VUMAT实现上述过程，ABAQUS-VUMAT是由应变驱动，随着载荷增加，首先读取各单层的材料信息和铺层信息的参数代码文件， 计算各子层压板内各个单层在局部材料坐标系下的刚度矩阵，再转换到整体坐标系下的单层刚度矩阵；

步骤(5)：再通过步骤(1)求取各子层压板的三维等效刚度和子层压板的应力应变；将子层压板的应力应变通过步骤(2)分解为子层压板内各个单层应力应变，并转换为局部材料坐标系下的单层应力应变；再根据步骤(3)判断每个单层是否出现损伤以及求取损伤变量；如果没有出现损伤，则更新应力应变后进入下一个增量步；如果出现损伤，则返回到步骤(4)通过损伤变量更新每个单层在整体坐标系下的刚度矩阵，再通过步骤(1)求取折减后的子层压板的三维等效刚度，计算子层压板三维等效刚度折减系数，并存储为SDV状态变量，更新应力应变后再进入下一个增量步；

所述过程四具体为：将过程一建立的模型主文件和过程三建立的ABAQUS-VUMAT用户子程序联合，使用ABAQUS/EXPLICT方法对低速冲击进行计算，进一步获得冲击力、位移、速度和加速度；即完成低速冲击载荷下复合材料多层厚板渐进失效特性的预测。

以下用基于上述过程应用的具体实施例子来说明本发明的实现效果：

在ABAQUS/CAE中建立包括碳纤维/环氧树脂复合材料多层厚板，冲锤以及支撑板的低速冲击有限元模型，如图1所示。其中复合材料多层厚板有两种铺层形式：

和平板大小为150×100×4mm，密度为

ρ＝1600kg/m³，总共分为16个单层，依次将每四个单层划分为一个子层压板，所以在厚度方向共有四个子层压板，只需要在厚度方向划分四个单元(每个单元1mm)。每个子层压板均用减缩积分三维实体单元C3D8R来仿真，内聚力单元层铺设在纤维方向不同的子层之间研究分层损伤，冲锤前端建成半球形，冲锤的质量为2kg,直径为1.6cm。冲锤的冲击能量分别为25J。

层合板下方有一个长方形撑框架模型，框架外尺寸与平板相同，并带有125×75mm的长方形开孔,冲锤和支撑框架的刚度和泊松比分别为

207.6GPa和0.26，密度为ρ＝7830kg/m³，框架的下表面固定。

利用ABAQUS/EXPLICT显示计算模拟冲锤冲击多层厚板的过程，如图2利用用户子程序VUMAT首先求取子层压板的等效刚度，得到平板在整体坐标系下的应力应变，并分解到每个单层判别损伤并求取相应的刚度比折减系数，并存储到状态变量SDV中，再更新应力应变。基于上述过程求取多层厚板渐进失效过程。

图3和图4分别为在25J冲击能量下铺层的冲击力-时间和冲击力-位移的曲线图，图5和图6分别为在25J冲击能量下的冲击力-时间和冲击力-位移的曲线图，均与试验值准确的吻合。所以本发明提出的多尺度模型可以较为准确的预测复合材料多层厚板在低速冲击下的渐进损伤失效特征。

本发明在ABAQUS软件的基础上进行用户子程序的开发，提出的多尺度模型建立子层压板和该子层压板内每个单层的转化关系，大大减少了计算量，能高效且较为准确预测复合材料多层厚板在低速冲击下的渐进损伤失效，为深入阐明复合材料结构的损伤失效特性、提升轻量化强度设计水平提供了技术支撑。

最后，需要注意的是，以上列举的仅是本发明的具体实施例。显然，本发明不限于以上实施例，还可以有很多变形。本领域的普通技术人员能从本发明公开的内容中直接导出或联想到的所有变形，均应认为是本发明的保护范围。