实时显示航拍照片覆盖区域的方法及系统与流程

本发明属于航拍航测领域，具体的涉及一种实时显示航拍照片覆盖区域的方法及系统。

背景技术：

目前无人机应用于航拍航测领域已经非常广泛，当无人机在执行航拍航测任务时，用户希望能够实时的了解当前拍摄照片的实际情况，如果有必要，可以根据实际情况对无人机进行一些路线或者姿态的干预，以及时的保障作业的质量。

目前市面上的解决技术由无人机飞控系统回传实时拍照的相关POS信息，相关地面软件根据飞控回传的POS信息，显示当前的曝光点在软件上。避免等到外业完毕做内业操作时才发现照片的重叠率、拍摄方向不满足要求，以及因此带来的时间和资源浪费。

为了解决上述问题，本发明提供了一种实时显示航拍照片覆盖区域的方法及系统，其能够使用户实时地了解当前飞机的拍照情况，能够以直观的方式观察到照片的拍摄区域、重叠率、拍照方向等信息。

技术实现要素：

本发明提供一种实时显示航拍照片覆盖区域的方法及系统，其避免等到外业完毕后，做内业操作时才发现照片的重叠率、拍摄方向不满足要求的问题。

本发明提供一种实时显示航拍照片覆盖区域的方法，包括以下步骤：

飞机上的拍照设备通过数传电台将曝光时刻的角度信息传送至地面站；

所述地面站将接收到的角度信息，发送至数学建模单元；

所述数学建模单元根据四元素理论，将角度信息进行计算，得到飞机实际拍照区域的坐标；

根据飞机实际拍照区域的坐标，图像处理单元在地图界面上进行范围划定，模拟显示实时的拍照区域范围；

重复上述四个步骤，绘制一条航线上的所有曝光点的拍照区域范围。

优选的是，曝光时刻的角度信息为俯仰角、横滚角和方向角。

优选的是，所述数学建模单元根据四元素理论，将角度信息进行计算，得到飞机实际拍照区域的坐标的具体步骤如下：

当飞机在俯仰角为0°、横滚角为0°、方向角为0°时，根据投射原理，得到实际拍照区域的坐标；

将俯仰角、横滚角、方向角旋转，使飞机的俯仰角为α、横滚角为β、方向角为γ时，所述数学建模单元根据四元素理论，在实际拍照区域的坐标的基础上，计算出飞机旋转后的实际拍照区域的坐标。

优选的是，当飞机在俯仰角为0°、横滚角为0°、方向角为0°时，根据投射原理，得到实际拍照区域的坐标的具体步骤为：

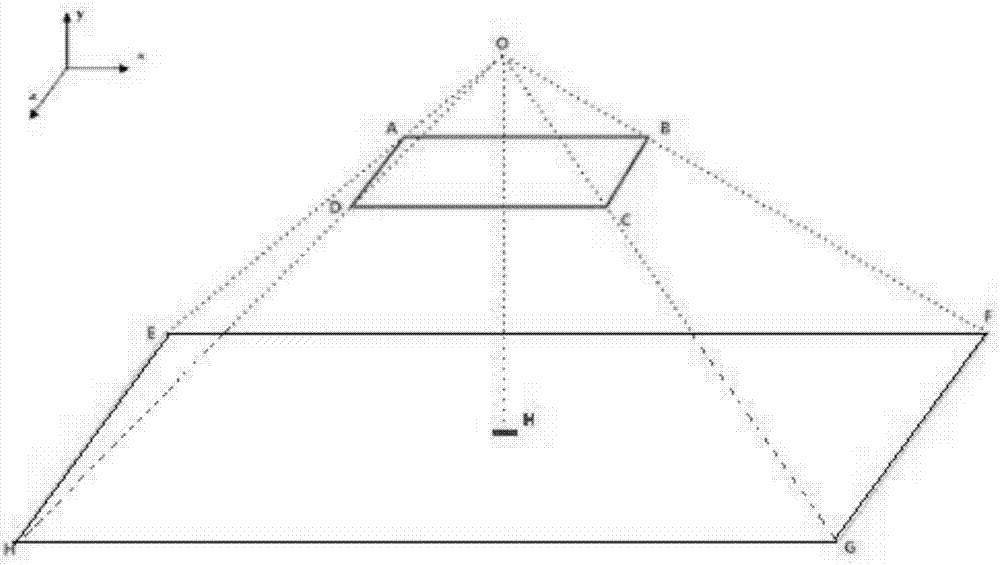
当飞机在俯仰角为0°、横滚角为0°、方向角为0°时，设拍照设备的四个顶点为A、B、C、D，并将A、B、C、D四个顶点投射在实际拍摄中的地面上，得到E、F、G、H四个点，E、F、G、H为实际拍照区域的坐标。

优选的是，将俯仰角、横滚角、方向角旋转，使飞机的俯仰角为α、横滚角为β、方向角为γ时的具体步骤为：

连接AE、BF、CG、DH各点并作延伸线，交于点O，以O点在地平面上的投影点H为坐标原点、飞机飞行方向为x轴、垂直地面向上为y轴、机翼方向为z轴建立空间三维直角坐标系，则俯仰角绕z轴旋转，横滚角绕x旋转，方向角绕y轴旋转，使飞机的俯仰角为α、横滚角为β、方向角为γ。

优选的是，所述数学建模单元根据四元素理论，在实际拍照区域的坐标的基础上，计算出飞机旋转后的实际拍照区域的坐标的具体步骤如下：

步骤1)当飞机的俯仰角为α时，A点偏移，得到A₁，设A点笛卡尔坐标为(x_A,y_A,z_A)，用四元数表示为p_A＝x_Ai+y_Aj+z_Ak，俯仰角旋转α角度时，A₁的坐标的四元数用矩阵(旋转轴单位矢量为<0,0,1>)表示为：

同样地，再进行横滚角β(旋转轴单位矢量为<1,0,0>)和方向角γ(旋转轴单位矢量为<0,1,0>)的旋转，对A₁(x_A1，y_A1，z_A1)→A₂(x_A2，y_A2，z_A2)、A₂(x_A2，y_A2，z_A2)→A₃(x_A3，y_A3，z_A3)的坐标变换，有

所以，A₃的坐标的四元素用矩阵表示为：

同理，得到B、C、D、O点后，再得到B₃、C₃、D₃、O₃点；

步骤2)根据点A₃、O₃，得出直线O₃A₃的方程为：

直线O₃A₃与地平面y＝0的交点为E₃，表示为：

同理，计算得出F₃、G₃、H₃，即当飞机在俯仰角为α、横滚角β、方向角γ情况下，得到实际拍照区域的四个点的坐标E₃、F₃、G₃、H₃。

本发明提供一种实时显示航拍照片覆盖区域的系统，包括：

数传电台，用于将曝光时刻的俯仰角、横滚角、方位角的角度信息回传给地面接收站；

地面接收站，用于接收所述数传电台传送的角度信息；

数学建模单元，用于根据四元素理论，将地面接收站发送的角度信息进行计算，得到飞机的实际拍照区域的坐标；

图像处理单元，用于根据实际拍照区域的坐标，在地图界面上进行范围划定，模拟显示实时的拍照区域范围；

其中，图像处理单元可以绘制一条航线上的所有曝光点的拍照区域范围。

优选的是，所述数学建模单元用于：

当飞机在俯仰角为0°、横滚角为0°、方向角为0°时，设拍照设备的四个顶点为A、B、C、D，并将A、B、C、D四个顶点投射在实际拍摄中的地面上，得到E、F、G、H四个点，E、F、G、H为实际拍照区域的坐标；

将俯仰角、横滚角、方向角旋转，使飞机的俯仰角为α、横滚角为β、方向角为γ时，根据四元素理论，在实际拍照区域的坐标的基础上，计算出飞机旋转后的实际拍照区域的坐标。

优选的是，将俯仰角、横滚角、方向角旋转，使飞机的俯仰角为α、横滚角为β、方向角为γ包括：

连接AE、BF、CG、DH各点并作延伸线，交于点O，以O点在地平面上的投影点H为坐标原点、飞机飞行方向为x轴、垂直地面向上为y轴、机翼方向为z轴建立空间三维直角坐标系，则俯仰角绕z轴旋转，横滚角绕x旋转，方向角绕y轴旋转，使飞机的俯仰角为α、横滚角为β、方向角为γ。

优选的是，根据四元素理论，在实际拍照区域的坐标的基础上，计算出飞机旋转后的实际拍照区域的坐标包括：

步骤1)当飞机的俯仰角为α时，A点偏移，得到A₁，设A点笛卡尔坐标为(x_A,y_A,z_A)，用四元数表示为p_A＝x_Ai+y_Aj+z_Ak，俯仰角旋转α角度时，A₁的坐标的四元数用矩阵(旋转轴单位矢量为<0,0,1>)表示为：

同样地，再进行横滚角β(旋转轴单位矢量为<1,0,0>)和方向角γ(旋转轴单位矢量为<0,1,0>)的旋转，对A₁(x_A1，y_A1，z_A1)→A₂(x_A2，y_A2，z_A2)、A₂(x_A2，y_A2，z_A2)→A₃(x_A3，y_A3，z_A3)的坐标变换，有

所以，A₃的坐标的四元素用矩阵表示为：

同理，得到B、C、D、O点后，再得到B₃、C₃、D₃、O₃点；

步骤2)根据点A₃、O₃，得出直线O₃A₃的方程为：

直线O₃A₃与地平面y＝0的交点为E₃，表示为：

同理，计算得出F₃、G₃、H₃，即当飞机在俯仰角为α、横滚角β、方向角γ情况下，得到实际拍照区域的四个点的坐标E3、F3、G3、H3。

有益效果

1、本发明提供的实时显示航拍照片覆盖区域的方法，其采用四元数理论来计算实际拍照的区域范围，能够直观地显示照片的拍摄范围、拍摄方向角度。

2、本发明提供的实时显示航拍照片覆盖区域的方法，其能够直观地显示拍摄照片的重叠率和覆盖范围。

3、本发明提供的实时显示航拍照片覆盖区域的方法，其采用图像处理单元可以根据实际拍照区域的坐标，在地图界面上进行范围划定，根据不同的行业，可以有不同的图形来模拟显示实时的拍照区域范围。

4、本发明提供的实时显示航拍照片覆盖区域的系统，其采用数据建模单元，能够以直观的方式观察到照片的拍摄区域、重叠率、拍照方向等信息，从而在执行外业任务时就基本能判断任务的执行情况，并及时作出调整。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。

图1为本发明提供的实时显示航拍照片覆盖区域方法中的航拍区域示意图；

图2为本发明提供的俯仰角为0°、横滚角为0°、方向角为0°时的实际拍照区域的示意图；

图3为本发明提供的俯仰角为α、横滚角为0、方位角为0时的实际拍照区域的示意图；

图4为本发明提供的在地图软件上的俯仰角为α、横滚角为0、方位角为0时的实际拍照区域；

图5为本发明提供的在俯仰角为α、横滚角为0、方位角为0时，地图软件上绘制的一条航线上所有曝光点的实际拍照区域。

具体实施方式

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

本发明涉及的数学计算及应用理论为四元数，为了方便计算空间中的旋转，引入四元素理论，作为用于描述现实空间的坐标表示方式，人们在复数的基础上创造了四元数并以a+bi+cj+dk的形式说明空间点所在位置。其中，i、j、k作为一种特殊的虚数单位参与运算，并有以下运算规则：i⁰＝j⁰＝k⁰＝1，i²＝j²＝k²＝-1。

对四元数a+bi+cj+dk可以用矩阵表示为或(其中代表虚数部分的三维向量)。

对三维坐标系中一个的点，设其笛卡尔坐标为(x，y，z)，则用纯四元数(实部为0的四元数)可表示为xi+yj+zk或其中代表矢量<x，y，z>。

对一个单位四元数，可以仿照单位复数用欧拉公式表示为：

那么对于一个纯四元数p＝ai+bj+ck，将其绕单位向量为的旋转轴旋转θ后，所得点p′用四元数可以表示为：

p′＝qpq-1

带入计算，并记则有

p′＝qpq^-1＝[c-(xi+yj+zk)s](ai+bj+ck)[c+(xi+by+ck)s]

展开后，可以得到用矩阵表示的四元数p′＝a′i+b′j+c′k如下：

这就是用四元数完成的三维空间点的一次旋转变换。

将上述四元数的理论应用到本发明，本发明提供一种实时显示航拍照片覆盖区域的方法，包括以下步骤：

飞机上的拍照设备通过数传电台将曝光时刻的俯仰角、横滚角、方向角的角度信息传送至地面站；

所述地面站将接收到的角度信息，发送至数学建模单元；

所述数学建模单元根据四元素理论，将角度信息进行计算，得到飞机实际拍照区域的坐标的具体步骤如下：

结合如图2，其为本发明提供的俯仰角为0°、横滚角为0°、方向角为0°时的实际拍照区域的示意图。在飞机俯仰角为0，横滚角为0，方向角为0°时情况下，设搭载的相机传感器4个顶点为A、B、C、D(示意图中为方便起见进行了扩大，实际的相机传感器很小)，相机实际拍摄区域4个顶点为E、F、G、H，其中EFGH各点分别是ABCD各点在实际拍摄中在地面的投射；连接AE、BF、CG、DH各点并作延伸线，最终有一个交点O。以O点在地平面上的投影点H为坐标原点、飞机飞行方向为x轴、垂直地面向上为y轴、机翼方向为z轴建立空间三维直角坐标系，则俯仰角即绕z轴旋转，横滚角即绕x旋转，航向角即绕y轴旋转，使飞机的俯仰角为α、横滚角为β、方向角为γ。

飞机在俯仰角为α情况下，原图中各点分别偏移，得到下标为1的点。下以A→A₁的坐标变换来进行说明(图3为本发明提供的俯仰角为α、横滚角为0、方位角为0时的实际拍照区域的示意图)：

设A点笛卡尔坐标为(x_A，y_A，z_A)，则其可用四元数表示为p_A＝x_Ai+y_Aj+z_Ak。

则旋转变化后，A₁的坐标(x_A1，y_A1，z_A1)的四元数用矩阵表示为：(旋转轴单位矢量为<0,0,1>)

同样地，再进行横滚角β(旋转轴单位矢量为<1,0,0>)和方向角γ(旋转轴单位矢量为<0,1,0>)的旋转，对A₁(x_A1，y_A1，z_A1)→A₂(x_A2，y_A2，z_A2)、A₂(x_A2，y_A2，z_A2)→A₃(x_A3，y_A3，z_A3)的坐标变换，有

将之前的结论带入，则有：

同理地，可以得到其余B、C、D、O点与B₃、C₃、D₃、O₃点。

直线O₃A₃的方程为

则对其与地平面y＝0的交点E₃，有

其余各点F₃G₃H₃各点的求解过程类似，最终求得飞机在俯仰角为0、横滚角0、方向角0情况下实际拍照区域为E、F、G、H而当飞机在俯仰角为α、横滚角β、方向角γ情况下的实际拍照区域E₃F₃G₃H₃各点坐标。

根据飞机实际拍照区域的坐标，图像处理单元在地图界面上进行范围划定，模拟显示实时的拍照区域范围，在软件地图界面将该区域范围以黄色边框、半透明蓝色背景进行图像处理，以模拟显示实时的拍照范围；本发明在航拍航测行业可以相机投射的四边形区域来直观的显示给用户，在管线巡查，森林防火等行业也可以根据拍照器材的参数显示映射的四边形区域；而在农业植保等行业还可以根据其作业半径将其映射为一个圆形的投射区域。如附图4为本发明提供的在地图软件上的俯仰角为α、横滚角为0、方位角为0时的实际拍照区域。

重复上述步骤，绘制一条航线上的所有曝光点的拍照区域范围。图5为本发明提供的在俯仰角为α、横滚角为0、方位角为0时，地图软件上绘制的一条航线上所有曝光点的实际拍照区域，由图5可以看出，当飞机平稳飞行时，会根据当前软件设定的相机参数以及拍照参数计算出目前相机拍照范围投射到地面上的区域，由于上图飞机航向角为正东，横滚角和俯仰角都处于0度，所以目前绘制的拍照区域为水平的矩形，从中，可以直观地显示照片的拍摄范围，拍摄方向角度。直观地显示任务的重叠率和覆盖范围。

模拟照片拍摄区域显示，以半透明四边形叠加或者覆盖在地图上的方式显示照片所拍摄的实际范围；模拟照片拍摄区域以及曝光点显示，以半透明四边形叠加或者覆盖在地图上的方式显示照片所拍摄的实际范围，并在地图上曝光点位置以图形来进行标记。

本发明还提供了一种实时显示航拍照片覆盖区域的系统，包括：

数传电台，用于将曝光时刻的俯仰角、横滚角、方位角的角度信息回传给地面接收站，所述数传电台设置在所述飞机上；

地面接收站，用于接收所述数传电台传送的角度信息，所述地面接收站与搜书数传电台通讯连接，可以无线，蓝牙等等连接方式；

数学建模单元，其与所述地面接收站用于根据四元素理论，将地面接收站发送的角度信息进行计算，得到飞机的实际拍照区域的坐标具体步骤包括：

当飞机在俯仰角为0°、横滚角为0°、方向角为0°时，设拍照设备的四个顶点为A、B、C、D，并将A、B、C、D四个顶点投射在实际拍摄中的地面上，得到E、F、G、H四个点，E、F、G、H为实际拍照区域的坐标；

连接AE、BF、CG、DH各点并作延伸线，交于点O，以O点在地平面上的投影点H为坐标原点、飞机飞行方向为x轴、垂直地面向上为y轴、机翼方向为z轴建立空间三维直角坐标系，则俯仰角绕z轴旋转，横滚角绕x旋转，方向角绕y轴旋转，使飞机的俯仰角为α、横滚角为β、方向角为γ；

当飞机的俯仰角为α时，A点偏移，得到A₁，设A点笛卡尔坐标为(x_A,y_A,z_A)，用四元数表示为p_A＝x_Ai+y_Aj+z_Ak，俯仰角旋转α角度时，A₁的坐标的四元数用矩阵(旋转轴单位矢量为<0,0,1>)表示为：

同样地，再进行横滚角β(旋转轴单位矢量为<1,0,0>)和方向角γ(旋转轴单位矢量为<0,1,0>)的旋转，对A₁(x_A1，y_A1，z_A1)→A₂(x_A2，y_A2，z_A2)、A₂(x_A2，y_A2，z_A2)→A₃(x_A3，y_A3，z_A3)的坐标变换，有

所以，A₃的坐标的四元素用矩阵表示为：

同理，得到B、C、D、O点后，再得到B₃、C₃、D₃、O₃点；

根据点A₃、O₃，得出直线O₃A₃的方程为：

直线O₃A₃与地平面y＝0的交点为E₃，表示为：

同理，计算得出F₃、G₃、H₃，即当飞机在俯仰角为α、横滚角β、方向角γ情况下，得到实际拍照区域的四个点的坐标E3、F3、G3、H3；所述数学建模单元与所述地面接收站连接，接收地面接收站发送的信息，所述数学建模单元可以设置在PC上，即地面站接收到该数据后，再转发给运行在地面站PC上的数学建模单元；

图像处理单元，其与所述数学建模单元连接，其根据飞机实际拍照区域的坐标，图像处理单元在地图界面上进行范围划定，模拟显示实时的拍照区域范围，在软件地图界面将该区域范围以黄色边框、半透明蓝色背景进行图像处理，以模拟显示实时的拍照范围；本发明在航拍航测行业可以相机投射的四边形区域来直观的显示给用户，在管线巡查，森林防火等行业也可以根据拍照器材的参数显示映射的四边形区域；而在农业植保等行业还可以根据其作业半径将其映射为一个圆形的投射区域。如附图4为本发明提供的在地图软件上的俯仰角为α、横滚角为0、方位角为0时的实际拍照区域；

重复上述步骤，绘制一条航线上的所有曝光点的拍照区域范围。图5为本发明提供的在俯仰角为α、横滚角为0、方位角为0时，地图软件上绘制的一条航线上所有曝光点的实际拍照区域，由图5可以看出，当飞机平稳飞行时，会根据当前软件设定的相机参数以及拍照参数计算出目前相机拍照范围投射到地面上的区域，由于上图飞机航向角为正东，横滚角和俯仰角都处于0度，所以目前绘制的拍照区域为水平的矩形，从中，可以直观地显示照片的拍摄范围，拍摄方向角度。直观地显示任务的重叠率和覆盖范围。

本发明提供的系统依赖上述方法而形成的系统，具有所以本发明提供的实时显示航拍照片覆盖区域的系统具有本发明提供的实时显示航拍照片覆盖区域的方法的有益效果。

本发明根据当前飞机搭载的相机参数、用户设置的拍照参数能够计算出飞机在拍照时刻照片覆盖范围，再根据飞机拍照时刻的姿态角及航向角，将该区域进行几何变换，从而能够精确的计算飞机在拍照时刻照片能够覆盖的范围；最后根据变换后的覆盖数据以直观的方式绘制在地图上，其中，单张的模拟显示能够反映本次照片的覆盖范围，拍摄角度，多张的模拟显示能够反映照片的重叠率。

使用本发明的技术时，用户能够实时地了解当前飞机的拍照情况，能够以直观的方式观察到照片的拍摄区域、重叠率、拍照方向等信息，从而在执行外业任务时就基本能判断任务的执行情况并及时作出调整。避免等到外业完毕做内业操作时才发现照片的重叠率、拍摄方向不满足要求，以及因此带来的时间和资源浪费。

尽管已描述了本发明的优选实施例，但本领域内的技术人员一旦得知了基本创造性概念，则可对这些实施例作出另外的变更和修改。所以，所附权利要求意欲解释为包括优选实施例以及落入本发明范围的所有变更和修改。

显然，本领域的技术人员可以对本发明进行各种改动和变型而不脱离本发明的精神和范围。这样，倘若本发明的这些修改和变型属于本发明权利要求及其等同技术的范围之内，则本发明也意图包含这些改动和变型在内。