一种基于超声图像和三维模型的肝脏体积测量方法与流程

本发明涉及医疗技术领域，具体为一种基于超声图像和三维模型的肝脏体积测量方法。

背景技术：

我国为病毒性肝炎的高发地区，主要为慢性乙型和丙型肝炎，这些疾病很容易发展成肝硬化和肝癌。对肝硬化和肝癌的治疗手段主要是肝切除和肝移植手术，这类手术前需要得到供体和受供体肝脏的准确体积。研究表明，活体肝脏移植手术中，供体应至少保留全肝脏体积的30％，而受供体接收的肝脏体积应大于肝脏体积的40％，因此术前肝脏体积测量的准确度直接影响到手术方案的选择和成功率。

目前肝脏体积的测量方法有ct法、mr法、三维超声法和公式法，这些方法各有利弊。ct法可以得到比较准确的肝脏体积，但ct法需要注射造影剂，而且扫面过程中x射线对人体有辐射，不能反复运用；mr法费用非常昂贵，也不适合进行多次测量，对于需要多次扫描连续观察肝脏的状况的患者，mr扫描非常不适合；三维超声扫描方法对人体无任何伤害，成像快速方便，但由于超声本身成像原理的限制，超声图像的分辨率较低；公式法是根据大量的统计结果提出的一种肝脏体积近似的估计方法，它根据人的身高和体重等参数得到体表面积，进而得到肝脏体积，但是该方法测量的误差较大。因此需要一种新的肝脏体积的测量方法实现无损害、安全、反复、快捷的测量肝脏体积，为此，我们提出了一种基于超声图像和三维模型的肝脏体积测量方法投入使用，以解决上述问题。

技术实现要素：

本发明的目的在于提供一种基于超声图像和三维模型的肝脏体积测量方法，以解决上述背景技术中提出的问题。

为实现上述目的，本发明提供如下技术方案：一种基于超声图像和三维模型的肝脏体积测量方法，该基于超声图像和三维模型的肝脏体积测量方法的具体步骤如下：

s1：利用超声图像中需要提取的目标与其背景在灰度特征上的差异，把图像视为具有不同灰度级的区域的组合，通过选取阈值，将目标区域从背景区域中分离；

s2：将分离出的目标区域分割成多块较小的基本区域，然后根据特定的均匀性判据而合并；

s3：采集合并后的目标区域，在三维模型坐标中，建立三维图像模拟，并形成三维体数据；

s4：针对形成的三维体数据采用椭球模型进行匹配，得到椭球初始轮廓，随后初始椭球模型按照一定规则离散化生成三角网络图像模型；

s5：采集待检测脏器的三维图像，然后确定待检测脏器的上下极和中心轴，再选择相应的旋转角度，系统自动生成或手动勾画不同角度脏器的边缘，重建完整的立体轮廓，通过软件后处理，得到被测脏器的三维体积参数。

优选的，所述步骤s1中，阈值的选取应根据目标区域的大小进行选择，如果阈值选择过大，一些目标物将被视作背景，若阈值选择过小，则会将背景转换成目标物，造成目标区域的特征失真。

优选的，所述步骤s2中，将目标区域作为原始分割结果，只要当前的分裂结果不能保证足够的均匀性，就将其分裂成四个方形区域，将相邻且具有相似特征的区域进行合并，而将具有明显不均匀性特征的区域进行分裂。

优选的，所述步骤s4中，在椭球初始轮廓的形成过程中，首先利用初始区域生长方法对目标区域中间层图像进行椭圆匹配，然后以匹配椭圆的中心作为椭球的中心，以匹配椭圆的x轴和y轴分别作为椭球的x轴和y轴，以穿过匹配椭圆的中心，得到椭球三维初始轮廓。

优选的，所述步骤s5中，旋转角度a有6°、9°、15°和30°四周不同角度，不同角度的脏器边缘共计180/a个平面。

与现有技术相比，本发明的有益效果是：本发明采用三维超声体积测量肝脏肿瘤的体积，测量时不受被测结构的不规则形态影响，有较高的准确性和可重复性，并利用超声图像能够精确的监测被测结构的大小变化和形态学的变化，能够准确预估肝脏危险因素的危险程度，从而能够对症下药达到很好的治疗效果。

附图说明

图1为本发明工作流程图；

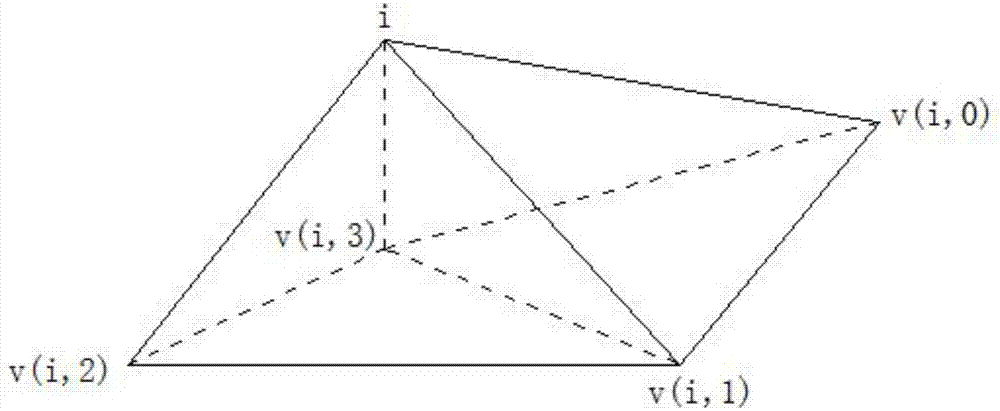
图2为本发明三维基本单元结构示意图；

图3为本发明椭球模型的离散化过程结构示意图。

具体实施方式

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

请参阅图1，本发明提供一种技术方案：一种基于超声图像和三维模型的肝脏体积测量方法，该基于超声图像和三维模型的肝脏体积测量方法的具体步骤如下：

s1：利用超声图像中需要提取的目标与其背景在灰度特征上的差异，把图像视为具有不同灰度级的区域的组合，通过选取阈值，将目标区域从背景区域中分离，阈值的选取应根据目标区域的大小进行选择，如果阈值选择过大，一些目标物将被视作背景，若阈值选择过小，则会将背景转换成目标物，造成目标区域的特征失真；

s2：将分离出的目标区域分割成多块较小的基本区域，然后根据特定的均匀性判据而合并，将目标区域作为原始分割结果，只要当前的分裂结果不能保证足够的均匀性，就将其分裂成四个方形区域，将相邻且具有相似特征的区域进行合并，而将具有明显不均匀性特征的区域进行分裂；

s3：采集合并后的目标区域，在三维模型坐标中，建立三维图像模拟，并形成三维体数据；

s4：针对形成的三维体数据采用椭球模型进行匹配，得到椭球初始轮廓，随后初始椭球模型按照一定规则离散化生成三角网络图像模型，在椭球初始轮廓的形成过程中，首先利用初始区域生长方法对目标区域中间层图像进行椭圆匹配，然后以匹配椭圆的中心作为椭球的中心，以匹配椭圆的x轴和y轴分别作为椭球的x轴和y轴，以穿过匹配椭圆的中心，得到椭球三维初始轮廓；

s5：采集待检测脏器的三维图像，然后确定待检测脏器的上下极和中心轴，再选择相应的旋转角度，系统自动生成或手动勾画不同角度脏器的边缘，重建完整的立体轮廓，通过软件后处理，得到被测脏器的三维体积参数，旋转角度a有6°、9°、15°和30°四周不同角度，不同角度的脏器边缘共计180/a个平面。

请参阅图2，三维形变模型的活动表面定义为三维空间(x,y,z)上的一个参数化曲面，三维形变模型变形过程就是活动表面在内力和外力的共同作用下向目标物体边缘靠近的过程，内力保持活动表面的光滑性和连续性，三角网络模型是三维形变模型的一种离散化表达方式，一个三角基本单元由一个顶点i，和它周围的四个相邻点v(i，0)、v(i，1)、v(i，2)、v(i，3)组成，这些相邻点v(i，0)、v(i，1)、v(i，2)、v(i，3)又分别作为相邻三角基本单元的顶点，再与其周围的四个相邻点形成新的三角单元，其中在内力的计算中，分别计算包含顶点i的各三角面片的单位法向量ni,k，通过计算加权和确定顶点i的单位法向量ri，在三角网络模型中，顶点i和邻接点v(i，k)之间的连接向量di,k定义为

di,k＝pi-pv(i,k)

其中，pi表示三角网络模型中每个顶点的位置，将di,k归一化，得到顶点i和邻接点v(i，k)之间的单位连接向量di,k，表示为

由i、v(i，k)和v(i，k+1)组成的三角面片法向量ni,k定义为

ni,k＝di,k×di,k+1

将ni,k归一化，得到三角面片的单位法向量ni,k定义为

顶点i的法向量ri定义为顶点i周围的四个三角面片单位法向量ni,k的加权平均值，为

顶点i的单位法向量ri定义为

然后分别计算法向量ri与各三角面片的发向量ni,k之差，通过计算加权和确定顶点i的曲率ci，在三角网络模型中，顶点i与相邻的第k个三角面片之间的曲率定义为顶点法向量ri与曲面法向量之差，顶点i的曲率ci定义为顶点i与所有相邻三角面片曲率的加权平均值，ci的计算公式如下：

其中ri确定了内力的方向，ci确定了内力的大小，内力fi,k定义为

请参阅图3，椭球的三维初始轮廓将按照三角基本单元结构进行离散化，形成三角网络模型，其离散化过程为：首先在椭球上的每一层x-y平面上进行相同数量的采样，本发明中分别对每层采样点数选用18、36、72进行，并最终选定为每层36个点，即每隔10°采集一个点，采样点过密不仅运算较为复杂，而且形变时容易产生交叉重叠，相反采样点过疏则会影响最后的分割精度；其次将每一层的采样点按采样次序依次连接起来；最后连接相邻的两层中同一角度的采样点，最终得到离散的椭球模型。

尽管已经示出和描述了本发明的实施例，对于本领域的普通技术人员而言，可以理解在不脱离本发明的原理和精神的情况下可以对这些实施例进行多种变化、修改、替换和变型，本发明的范围由所附权利要求及其等同物限定。