基于多目标遗传规划算法的序贯测试优化方法与流程

本发明属于电子系统故障诊断
技术领域：
，更为具体地讲，涉及一种基于多目标遗传规划算法的序贯测试优化方法。
背景技术：
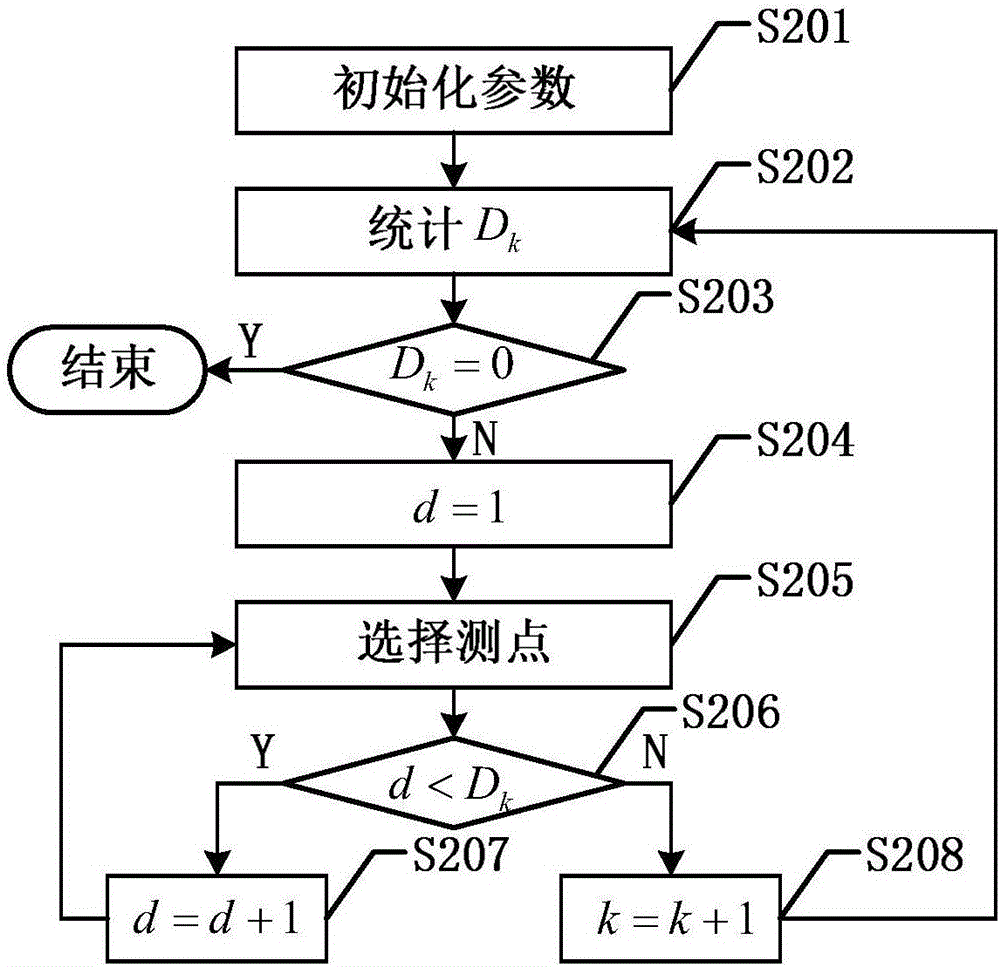
：在电子系统故障诊断技术中，序贯测试问题被定义为一个五元组问题(S,P,T,C,D)。其中，S＝{s0,s1,s2,…,sM}表示系统故障状态的有限集，其中s0表示系统没有故障发生的状态，s1到sM表示系统发生不同故障的状态。P＝{p0,p1,p2,…,pM}是各个系统状态发生的先验故障概率向量。假设系统只能处于某个故障状态或无故障状态，需要对先验故障概率向量P进行归一化。T＝{t1,t2,…,tN}是系统N个可用的测试集合。C＝{c1,c2,…,cN}表示对应的测试代价向量，其中测试代价采用测试时间、测试费用及其他相关因素进行衡量。D是一个N×(M+1)阶的0-1矩阵，其每个元素代表测试与系统故障的关系，被定义为故障-测试依赖矩阵。对于测试tj，如果tj能诊断出故障状态si，那么dij＝1，否则dij＝0，其中i＝0,1,…,M，j＝1,2,…,N。显然对于无故障状态s0，对任意j，均有d0j＝0。在单目标序贯测试问题中，测试时间、测试费用等测试相关的参数都被归一化为测试代价C，然而在实际生产中，部分系统在对于不同测试指标上(例如测试时间、测试费用)的需求不一定一致，即在不同优化目标存在不一致并很有可能产生冲突，因此需要找出符合条件的一组最优解可以兼顾系统对于不同测试指标的需求，该问题实质上是一个多目标优化问题。在实际应用中，人们经常会遇到多目标设计和决策的问题。为了解决多目标优化问题，为其建立了一个通用的数学模型。首先要确定它的决策变量，一般情况下，可把决策变量X看作n维欧氏空间En的一个点，也即：X＝(x1,x2,...,xn)∈En该决策变量满足以下约束条件：gi(x)≤0,i＝1,2,…,Phj(x)＝0,j＝1,2,…,Q其中，gi(x)≤0表示第i个不等式约束，P表示不等式约束的数量，hj(x)＝0表示第j个等式约束，Q表示等式约束的数量。假设有R个优化目标，且各个优化目标fr(X)之间相互冲突，r＝1,2,…,R，整体优化目标可表示为：寻求使在满足约束gi(x)≤0和hj(x)＝0的同时达到最优。在大多数情况下，由于多目标优化问题的各个目标是相互冲突的，一个子目标的改善有可能会引起其它子目标性能的降低，要想使得多个目标同时达到最优是不可能的，因而在求解多目标优化问题时只能对各个子目标进行协调和折中处理，使各个子目标函数都尽可能地达到最优。多目标优化问题与单目标优化问题有着本质的区别，多目标优化中的最优解，通常称之为Pareto(帕累托)最优解。设Xp和Xq是任意两个同时满足约束gi(x)≤0和hj(x)＝0的不同解，称Xp支配Xq，则必须满足下列二个条件：(1)对所有的子目标，Xp不比Xq差，即fr(Xp)≤fr(Xq)；(2)至少存在一个子目标，使Xp比Xq好，即使得fr′(Xp)＜fr(Xq)。在多目标优化问题的所有可行解中，若存在某个解，该解未被其他解支配，这个解称为Pareto最优解(非支配解)。理论上，多目标优化算法在找到一个Pareto最优解后就可以停止，但一个问题通常会有多个Pareto最优解，决策者需要根据实际情况选出最合适的Pareto最优解，因此多目标优化问题的目标就是找出所有的Pareto最优解。遗传算法是一类模拟生物自然选择和自然进化的随机搜索算法，具有隐含的并行性和在全局解空间进行搜索的能力，它一次运行便能得到一组最优解，遗传规划是遗传算法的扩展，是一种搜索寻优技术，主要通过效仿生物的进化和遗传，根据优胜劣汰的原则，使所要解决的问题从初始解一步步地逼近最优解，主要进化过程为种群初始化、挑选、交叉和变异。遗传规划中的个体一般表现为树状结构，有着灵活处理结构和大小不预先确定问题的优点，一般常用于解决符号回归问题。序贯测试问题中的故障诊断树和遗传规划个体表达都是采用二叉树形结构来表示的，因此可以遗传规划来解决序贯测试问题的方法。在公开号为“CN105629156A”的专利中，就公开了一种“基于遗传规划的模拟电路故障测试最优序贯搜索方法”，在该方法中将模拟电路的故障诊断树看成遗传规划的一个个体，然后采用遗传规划的算法来进化求出最优个体解。然而该方法中只考虑了测试代价一个优化目标，无法适用于存在多个测试指标作为优化目标的系统，需要进一步的改进。技术实现要素：本发明的目的在于克服现有技术的不足，提供一种基于多目标遗传规划算法的序贯测试优化方法，针对存在多个测试指标作为优化目标的系统，求取序贯测试的故障诊断树的Pareto最优解，为系统测试人员提供指导。为实现上述发明目的，本发明基于多目标遗传规划算法的序贯测试优化方法包括以下步骤：S1：根据系统的测试依赖矩阵随机生成H个故障诊断树，H的大小根据需要确定；S2：令迭代次数w＝1；S3：分别计算种群中每个个体的测试指标值Fhr，h＝1,2,…,H，r＝1,2,…,R，R表示测试指标的数量；根据测试指标值Fhr对种群中的个体进行分组，分组的具体步骤包括：S3.1：初始化集合A等于当前种群，令分组序号v＝1；S3.2：从集合A中搜索每个测试指标值Fhr极值对应的个体，如果测试指标的优化目标是尽可能大，则选择最大值对应的个体，如果测试指标的优化目标是尽可能小，则选择最小值对应的个体；S3.3：从集合A中筛选出未被测试指标值Fhr极值支配的个体；S3.4：将本轮筛选中步骤S3.2和步骤S3.3得到的个体构成第v个分组，并将该分组中的个体从集合A中删除；S3.5：判断是否集合A为空，如果是，分组结束，否则进入步骤S3.6；S3.6：令v＝v+1，返回步骤S3.2；S4：计算当前种群中每个个体的适应度值λh＝αh-0.5βh，其中αh＝0.5(V-vh+1)，vh表示个体h所属的分组序号，Gh表示个体h所属分组中除该个体以外其他个体构成的集合，γhh′表示拥挤距离，其计算公式如下：其中，δshare表示预设距离阈值，h′∈Gh；S5：根据步骤S4计算的各个个体的适应度，选择得到父个体集合；S6：将父个体集合中的个体随机分为H/2组，然后以组为单位，比较每组中的两个个体是否存在故障集相同的结点，如果某组中的两个个体不存在故障集相同的结点，则该组不进行交叉操作，如果某组中的两个个体存在故障集相同的结点，首先删除大小等于M-1或等于1的相同故障集，M表示故障集S中故障数量，在剩余的相同故障集中任意选择一个故障集，交换该故障集结点及其子树；S7：对交叉后得到的个体进行变异操作，其变异方法为：对于种群中的每个个体，随机选择一个节点，若该节点只包含一个故障，则重新选择，若该节点包含若干个故障且有能分割对应故障集的可用测点，则从该节点的可用测点中随机选择一个与之前使用过的测点都不相同的测点，将以该节点为根节点的子树从故障诊断树中删除，用新选出的测点重新生成相应的子树；S8：判断是否w＜W，W表示最大迭代次数，如果是，进入步骤S9，否则进入步骤S10；S9：令w＝w+1，返回步骤S3；S10：从最终代种群中搜索每个测试指标值Fhr极值对应的个体，再筛选出未被测试指标值Fhr极值支配的个体，作为本系统序贯测试的非支配故障诊断树。本发明基于多目标遗传规划算法的序贯测试优化方法，首先初始化得到故障诊断树种群，采用多目标遗传规划的方法对故障诊断树进行选择、交叉和变异，在每代迭代时，对故障诊断树个体进行分组，每个个体的适应度由分组适应度和拥挤距离计算得到，经过多次迭代后从最终代种群中选择非支配的个体作为本系统序贯测试的非支配故障诊断树。经实验验证可知，本发明可以得到存在多个测试指标作为优化目标的序贯测试的故障诊断树的Pareto最优解，供系统测试人员选择，从而为系统测试人员提供指导。附图说明图1是本发明基于多目标遗传规划算法的序贯测试优化方法的具体实施方式流程图；图2是本实施例中故障诊断树的生成方法；图3是本发明中种群个体分组方法流程图；图4是本发明中分组适应度确定示意图；图5是故障诊断树个体交叉的示例图。具体实施方式下面结合附图对本发明的具体实施方式进行描述，以便本领域的技术人员更好地理解本发明。需要特别提醒注意的是，在以下的描述中，当已知功能和设计的详细描述也许会淡化本发明的主要内容时，这些描述在这里将被忽略。图1是本发明基于多目标遗传规划算法的序贯测试优化方法的具体实施方式流程图。如图1所示，本发明基于多目标遗传规划算法的序贯测试优化方法的具体步骤包括：S101：种群初始化：种群初始化是根据系统的测试依赖矩阵随机生成H个故障诊断树，H的大小根据需要确定。故障诊断树的生成方法可以根据需要来选择，图2是本实施例中故障诊断树的生成方法。如图2所示，本实施例中所采用的故障诊断树生成方法包括以下步骤：S201：初始化参数：令根节点p0为故障集，即p0＝S，令层数初始值k＝0。S202：统计第k层故障集节点数量Dk。S203：判断是否Dk＝0，如果不是，进入步骤S204，否则故障诊断树生成结束。S204：令故障集节点序号d＝1。S205：选择测点：首先确定当前测点节点的可用测点集X＝T-T′，T′表示当前测点节点上层节点的测点集合，也就是说，当前测点不能与其上层节点中任何一个测点重复。从可用测点集φ中任意选择一个可以分割故障集Skd的测点t，Skd即表示第k层第d个故障集节点所对应的故障集，令测点节点tkd＝t，根据测点t的分割结果确定故障集Skd的子故障集Skd-left和Skd-right，如果不存在可以分割故障集Skd的测点，则不做任何操作。测点t对故障集Skd的分割是根据测试能否检测出故障来实现的，将故障集Skd中能够通过测点t检测的故障划分一个子故障集，不能通过测点t检测的故障划分为另一个子故障集，如果其中一个子故障集为空，则说明测点t不能完成对故障集Skd的分割。S206：判断是否d＜Dk，如果是，进入步骤S207，否则进入步骤S208。S207：令d＝d+1，返回步骤S205。S208：令k＝k+1，返回步骤S202。根据本实施例中提出的故障诊断树生成方法可能存在两个或几个故障构成的模糊组最终无法被分割的情况，这种情况可能通过后续操作来进行修正，也有可能由于测点集T中测点不够完备，最终仍然可能存在模糊组，因此应当尽可能多地将可使用的测点都加入测点集T。S102：令迭代次数w＝1。S103：个体分组：分别计算种群中每个个体的测试指标值Fhr，h＝1,2,…,H，r＝1,2,…,R，R表示测试指标的数量。本实施例中，测试指标采用测试时间Jt和测试费用Jc，计算公式分别如下：其中，p(si)表示故障si所发生的概率，i＝1,2,…,m，m表示故障数量，aij＝1表示当某个故障si发生时，测试tj能检测出该故障，aij＝0表示当故障si发生时不能被测试tj检测出；ctj为测试tj对应的测试时间，ccj为测试tj对应的测试代价。然后根据测试指标值Fhr对种群中的个体进行分组。图3是本发明中种群个体分组方法流程图。如图3所示，本发明中种群个体分组方法包括以下步骤：S301：初始化参数：初始化集合A等于当前种群，令分组序号v＝1。S302：筛选最优非支配个体：从集合A中搜索每个测试指标值Fhr极值对应的个体，如果测试指标的优化目标是尽可能大，则选择最大值对应的个体，如果测试指标的优化目标是尽可能小，则选择最小值对应的个体，这些个体分别拥有一个测试指标值在当前集合A中的极值，即为当前集合A的非支配解。以测试费用和测试时间为例，这两个测试指标的优化目标都是尽可能小，因此需要选择测试费用为最小值Cbest的个体和测试时间为最小值Tbest的个体。S303：筛选非支配个体：从集合A中筛选出未被测试指标值Fhr极值支配的个体。以测试费用和测试时间为例，非支配个体即为测试费用大于Cbest且测试时间小于Cbest的个体以及测试成本小于Tbest且测试时间大于Tbest的个体。S304：获取第v个分组：将本轮筛选中步骤S302和步骤S303得到的个体构成第v个分组，并将该分组中的个体从集合A中删除。可见，在每次筛选得到第v个分组后，集合A中剩余的个体都是被第1至第v个分组支配的个体，相应地，第v个分组为第1至第v-1个分组支配，因此可以称第v个分组为第v级非支配解，为之前的v-1个分组所支配。S305：判断是否集合A为空，如果是，分组结束，否则进入步骤S306。S306：令v＝v+1，返回步骤S302。S104：计算个体的适应度：在本发明中对种群进行了分组，定义每个分组存在一个分组适应度，然后采用拥挤距离来维持群体分布的多样性，因此每个个体的适应度是综合了其分组适应度和拥挤距离来计算的。记步骤S103得到的分组数量为V，当前种群中个体h的分组适应度αh＝0.5(V-vh+1)，h＝1,2,…,H，vh表示个体h所属的分组序号。图4是本发明中分组适应度确定示意图。如图4所示，第1个分组是未被其他个体支配的分组(第1级非支配解)，其中所有个体的分组适应度为0.5V，第2个分组是被支配一次的分组(第2级非支配解)，其中所有个体的分组适应度为0.5(V-1)，以此类推，最后一个分组，即被其他所有个体支配的分组(第V级非支配解)的个体的分组适应度为0.5。个体的拥挤距离可以通过计算同级别的两个个体在每个子目标上的距离差之和来求取。拥挤距离大的个体参与繁殖和进化的机会较多，从而维持种群的多样性。首先计算个体h与其分组中其他个体h′的拥挤距离γhh′：其中，δshare表示预设距离阈值，h′∈Gh，Gh表示个体h所属分组中除该个体以外其他个体构成的集合，Fh′r表示个体h′的测试指标值。个体h的累积拥挤距离βh的计算公式如下：根据个体h的分组适应度αh和累积拥挤距离βh，就可以计算得到个体h的适应度值λh＝αh-0.5βh。根据本发明中个体适应度的计算方法可知，个体适应度越大的个体，其适应能力越强，那么在新种群生成过程中越可能被保留。S105：选择父个体：根据步骤S104计算的各个个体的适应度，选择得到父个体集合。父个体集合中的个体数量仍然为H，这就表明，如果某些故障诊断树个体不被选择，那么就有另外的故障诊断树被选择次数超过一次。父个体集合的选择方法通常采用轮盘赌方法，也可以采用遗传算法中的其他父个体选择方法。轮盘赌方法的具体过程为：当前种群中所有个体的适应度累加求和，将每个个体的适应度除以适应度累加和得到该个体适应度占适应度累加和的份额，并将每个个体的适应度份额从小到大排列起来。随机生成一个在0到1之间的数，将这个随机数与个体份额进行比较，第一个拥有比当前随机数大的适应度份额的个体被选中放入父个体集合。这样一共进行H次选择，所有被选出的个体即可构成一个新的种群。S106：个体交叉：对步骤S105选择的父个体集合中的个体进行交叉操作。传统的遗传规划中的交叉操作，一般是交换两个个体中任意两个结点以及结点下各自所带的子树。但本发明所针对的故障诊断树较之于一般的二叉树有更多的条件限制，主要原因在于这种树的每一个子树都是由上级树中的故障集内容和所选测点所决定的，整棵树从上到下联系十分紧密，需要对交叉操作进行一些特殊的限制。因此本发明中个体交叉的具体方法如下：首先将父个体集合中的个体随机分为H/2组，然后以组为单位，比较每组中的两个个体是否存在故障集相同的结点，如果某组中的两个个体不存在故障集相同的结点，则该组不进行交叉操作，如果某组中的两个个体存在故障集相同的结点，为了防止交叉操作没有意义，先排除大小等于M-1或等于1的相同故障集，M表示系统故障集S中故障数量，再在在剩余的相同故障集中任意选择一个故障集，交换该故障集结点及其子树。为了提高交叉的意义与保证种群的多样性，每组个体最多只交换一次。图5是故障诊断树个体交叉的示例图。如图5所示，这两个故障诊断树个体中都有一个包含故障s1、s2、s5以及s12的故障集，交叉操作时应该将这两个故障集所在的节点以及它们各自的子树一并交换过来。S107：个体变异：对交叉后得到的个体进行变异操作，其变异方法为：对于种群中的每个个体，随机选择一个节点，若该节点只包含一个故障，则重新选择，若该节点包含若干个故障且有能分割对应故障集的可用测点，则从该节点的可用测点中随机选择一个与之前使用过的测点都不相同的测点，将以该节点为根节点的子树从故障诊断树中删除，用新选出的测点重新生成相应的子树。S108：判断是否w＜W，W表示最大迭代次数，如果是，进入步骤S109，否则进入步骤S110。S109：令w＝w+1，返回步骤S103。S110：筛选最终非支配个体：从最终代种群中搜索每个测试指标值Fhr极值对应的个体，再筛选出未被测试指标值Fhr极值支配的个体，也就是筛选出最终代种群中的非支配个体，作为本系统序贯测试的非支配故障诊断树。实施例为了更好地说明本发明的技术效果，采用一个具体实施例进行仿真验证。表1是本实例中电子系统含故障概率和测试代价的故障-测试依赖矩阵。表1本次实验验证的条件如下：CPU:奔腾G3250；操作系统：Windows7；编程语言：JAVA。遗传规划相关参数：种群大小：100；进化代数：100交叉率：0.8；变异率0.05。所采用的测试指标为测试费用和测试时间，拥挤距离的阈值δshare＝0.3。采用本发明进行序贯测试优化，得到12个Pareto最优解。表2是本实施例中Pareto最优解的测试费用和测试时间列表。测试时间测试费用3.30312.4873.78412.1184.61511.8664.70811.7444.72411.2754.819.4784.8758.0155.0357.9945.1987.6155.2327.225.3116.6015.5484.764表2从表2可以看出，该系统的最小测试费用为4.764，此时其测试时间为5.548，系统的最小测试时间为3.303，其对应的测试费用为12.487，系统无法同时获得最小的测试费用与时间。在Pareto最优解中，测试费用越大的个体测试时间越少，实际操作中可以根据需要从中选择最适合系统的解。可见，采用本发明可以得到存在多个测试指标作为优化目标的序贯测试的故障诊断树的Pareto最优解，为系统测试人员提供指导。尽管上面对本发明说明性的具体实施方式进行了描述，以便于本
技术领域：
的技术人员理解本发明，但应该清楚，本发明不限于具体实施方式的范围，对本
技术领域：
的普通技术人员来讲，只要各种变化在所附的权利要求限定和确定的本发明的精神和范围内，这些变化是显而易见的，一切利用本发明构思的发明创造均在保护之列。当前第1页1 2 3