基于多目标量子粒子群算法的无人机协同任务分配方法与流程

本发明属于计算机仿真与方法优化技术领域，涉及一种无人机协同任务分配方法，可用于无人机协同执行多种任务条件下，计算出多个优化目标下的无人机协同任务分配方案。

背景技术：

协同任务分配是多无人机协同任务规划中的关键技术之一，可以根据得到的任务执行区域的相关信息，为多架无人机提供任务执行指令序列，指派相应无人机进行相应任务。通过无人机协同任务分配，能够在任务执行之前进行预先的离线任务分配，可以利用任务区域的全局信息，为无人机执行任务提供理想的执行方案。

目前对无人机协同任务分配的研究主要是集中于单一目标函数下的模型求解，论文《基于milp模型的多无人机对地前期任务分配》(倪谣，周德云，马云红，贺宝财.基于milp模型的多无人机对地前期任务分配.火力与指挥控制,2008,33(11):62-65)针对无人机对地前期任务分配问题，考虑无人机前期任务和评估任务，采用混合整数线性规划(milp)求解无人机对地前期任务分配模型，但是由于milp是一种线性规划方法，其处理的模型规模不能太大，无法处理较复杂的任务分配问题。论文《复杂多约束uavs协同目标分配的一种统一建模方法》(赵明，苏小红，马培军，赵玲玲.复杂多约束uavs协同目标分配的一种统一建模方法.自动化学报,2012,38(12):2038-2048)针对多种情况给出了多无人机协同目标分配的统一建模方法，采用差分进化算法(de)对模型进行求解，有效完成了多无人机协同任务分配。论文《uav协同任务分配的改进dpso算法仿真研究》(王强,张安,宋志蛟.uav协同任务分配的改进dpso算法仿真研究.系统仿真学报,2014,26(5):1149-1155)将飞行时间、任务时间和威胁代价作为优化指标，利用离散粒子群算法实现了任务优先顺序约束下的无人机协同任务分配问题。但是这些论文中均采用了加权等方法将多种优化目标综合为一个目标函数，实际上是单目标的优化。这样处理优化目标会出现多个目标函数单位级别不同、不易比较、权值选取带有主观性等问题。因此，最好的解决方案就是针对多个目标函数可以同时得出多组具有不同性能倾向的结果供决策者进行选择。

多目标优化算法能够同时对多个优化目标进行优化，能够从不同优化目标的角度给出可行的无人机任务执行方案，是目前无人机协同任务分配研究的热点问题。论文《基于改进的多目标量子行为粒子群优化算法的多无人机协同任务分配》(施展,陈庆伟.基于改进的多目标量子行为粒子群优化算法的多无人机协同任务分配.南京理工大学学报(自然科学版),2012,36(6):945-951)采用多目标量子行为粒子群算法实现了最小代价和最大收益两种优化目标的同时优化。但该方法模型构造简单，约束较少，只实现了任务目标的分配，没有考虑任务执行的顺序。目前，对多目标无人机协同任务分配的研究较少，并没有一种能够解决复杂约束下多目标无人机协同任务分配问题的方法。

技术实现要素：

为了克服现有技术的不足，本发明提供一种基于多目标量子粒子群算法的无人机协同任务分配方法，给多个优化目标下的无人机协同任务分配问题求解提供一种合理可行的解决方案。

本发明解决其技术问题所采用的技术方案包括步骤如下：

步骤1，输入无人机数量nv、任务目标数量nt、无人机速度vuav、任务目标坐标位置post＝[post1,…,postnt]、无人机初始坐标位置posu＝[posu1,…,posunv]和无人机初始种群的规模p，其中post1代表第一个目标的坐标，posu1代表第一架无人机初始坐标位置；

步骤2，根据双层编码规则生成多个初始种群，具体内容如下：

2.1编码code＝[x1,…,xnv,y1,…,ynt]，其中x代表前期任务层编码，x1代表前期任务层第一个编码，前期任务层编码共nv维，且均是在[0,nt]内的整数，若为0则代表不进行前期任务；y代表评估任务层，y1代表评估任务层第一个编码，评估任务层共nt维，且均是在(1,nv+1)内的实数，实数的整数位是执行对应目标任务的无人机序号，整数相同的基因位实数的小数位大小代表对目标的执行顺序；

2.2采用kent混沌映射对种群初始化，kent混沌映射公式为

其中，r代表所产生的随机数序列，r^k代表序列中的第k个数，α＝0.4；

在初始化种群时，首先采用kent映射产生分布在[0,1]的随机数序列，然后通过解的取值范围将随机数序列转为个体解，第s个个体的初始解的产生如下所示：

xs1＝round(xmin+r^s(xmax-xmin))

ys1＝ymin+r^s(ymax-ymin)

其中，xs1代表第s个个体的前期任务层的第1个编码，ys1代表第s个个体的评估任务层的第1个编码，xmin＝0，xmax＝nt，ymin＝1，ymax＝nv+1；

步骤3，计算所有个体的适应度函数fitness，具体计算方法如下：

3.1将无人机对目标执行探测、识别、干扰和搜索任务统称为前期任务，无人机对目标前期任务执行成功概率矩阵其中pd11表示第1架无人机对第1个目标前期任务执行成功概率；

假设第i架无人机ui所携带任务载荷对第j个目标tj的任务执行成功概率是pdij；如果对于目标tj只有无人机ui对其进行前期任务，那么对于目标tj的任务执行成功概率pdj＝pdij；如果对于目标tj分配nj架无人机执行任务，则其前期任务执行成功概率

多无人机协同任务分配的目标前期任务执行成功概率指标其中，pj表示对第j个目标的最小前期任务执行成功概率要求；

3.2计算无人机生存概率矩阵其中ps11表示第1架无人机对第1个目标执行任务的生存概率；

假设第i架无人机ui在对第j个目标tj执行任务时的生存概率是psij，如果ui对目标执行任务是在目标确定生存的情况时，ui的生存概率psi＝psij；如果对目标执行评估任务，即目标已经被执行前期任务，则ui的生存概率psi＝psij(1-pdj)+pdj；

多无人机协同任务分配的无人机生存概率指标

3.3设第i架无人机ui完成自身所分配的任务时间为ti，计算任务完成时间

3.4计算个体适应度fitness，其中，f1是关于目标前期任务执行成功概率指标，f2是关于无人机生存概率的指标，f3是关于任务完成时间的指标，

其中k为ftime取值区间的最小正整数，constrains为个体违背约束的个数，对于个体，要求满足以下约束条件，即：

约束1：

约束2：

约束3：t(tj(a))＜t(tj(v)),j＝1,2,...,nt；

约束4：pdj≥pj,j＝1,2,...,nt；

约束5：

约束6：

约束7：

其中，表示无人机ui是否对目标tj执行前期任务，表示执行，表示不执行；表示无人机ui是否对目标tj执行评估任务，表示执行，表示不执行；t(tj(a))和t(tj(v))分别表示对第j个目标执行前期任务和评估任务的时间；

步骤4，计算当前种群的所有非支配解，并用所有非支配解构成外部种群np，外部种群np的规模为n；

步骤5，将初始种群内第w个个体本身作为其最优解xpbest,w，w＝1,2,…,p，根据非支配解距原点的距离越近越优秀的原则，采用轮盘赌方法进行选择，确定群体最优xgbest；

步骤6，判断当前迭代次数step是否等于最大迭代次数maxstep，若step＝maxstep则停止算法，输出外部种群np作为问题最终的解；若step≠maxstep则执行步骤7；

步骤7，根据量子粒子群优化算法，更新全部粒子，

其中，和u都是在(0,1)中的随机数，代表第r次迭代的粒子w的个体极值的第d维；代表第r次迭代的群体极值的第d维；代表第r+1次迭代的粒子w的第d维，β是惯性权值，

步骤8，对粒子采用修复算子进行修复，并计算各粒子的适应度，具体方法如下：

8.1采用针对前期任务约束的修复算子进行修复，具体操作步骤如下：

8.1.1判断粒子编码所代表的任务分配结果中的目标是否全被执行前期任务，若是则结束修复进行步骤8.2，否则进行步骤8.1.2；

8.1.2确定粒子编码所代表的任务分配结果中未被执行前期任务的目标序号tq以及被指派无人机最多的目标tp，其对应无人机有up1,up2,...,upn，n为分配到tp的无人机数量；

8.1.3判断编码所代表的任务分配结果中是否有未分配前期任务的无人机，若有，则在未分配前期任务的无人机u01,u02,...,u0m中，以对目标tq前期任务执行成功概率越高越好为原则，采用轮盘赌的方式选择一架无人机去对tq执行前期任务，结束修复并进行步骤8.2，否则进行步骤8.1.4；

8.1.4在分配至目标tp的无人机up1,up2,...,upn中，以对目标tp前期任务执行成功概率越低越好为原则，采用轮盘赌的方式选择一架无人机对tq执行前期任务，结束修复并进行步骤8.2；

8.2采用针对任务时序约束的修复算子，具体操作步骤如下：

8.2.1判断粒子编码所代表的任务分配结果中是否有无人机被分配执行同一目标ti上的前期任务和评估任务，若有则进行步骤8.2.2，否则进行步骤8.2.3；

8.2.2保持被分配执行同一目标ti上的前期任务和评估任务的无人机所执行的前期任务目标不变，并将在该前期任务目标上执行评估任务的无人机随机改为其他无人机；

8.2.3确定存有时序冲突的目标ti，并计算前期任务层结束后，未对目标ti进行前期任务的各无人机前往目标ti的累计航行距离；

8.2.4以离ti的累计航行距离越大越好为原则，采用轮盘赌的方式选取一架无人机对目标ti进行评估；

8.2.5计算修复后粒子的适应度fitness′，若修复后粒子适应度fitness′小于未修复之前的适应度则保留，否则维持原粒子编码不变；

步骤9，判断当前种群个体是否支配个体极值，即x′w＞xpbest，w，其中x′w代表当前种群第w个个体，若支配个体极值，则令xpbest,w＝x′w，否则维持xpbest,w不变；

步骤10，将迭代产生的新解与外部种群的解进行比较，根据算法中的外部种群添加策略判断是否将新解加入外部种群，外部种群添加策略如下：

第e个粒子经过迭代更新后为xe，迭代过程中的外部种群np＝(xnp1,xnp2,...,xnpn)，将xe与np中的非支配解进行比较，若存在xnps＞xe，s＝1,2,...,n，则维持np不变；若xe＞xnps，则将xnps从np中删除，并添加xe进入np；否则，直接添加xe进入np；

步骤11，若外部种群np规模超出设定值，从拥挤距离最小的粒子进行裁剪，直至恢复外部种群规模，以保持所设定的规模n，第e个粒子的拥挤距离dcrowde计算公式如下：

dcrowde＝dcrowde,1+dcrowde,2+dcrowde,3

其中，f1,e-1为f1的第e-1个数的值，e＞1且e＜|f1|，|f1|为f1中数据的个数，且f1,e-1＜f1,e＜f1,e+1，f1,max为f1中最大的数，f1,min为f1中最小的数；当e＝1或e＝|f1|时，dcrowde,1＝∞；

步骤12，将当前外部种群中最优粒子作为群体最优粒子xgbest；

步骤13，判断是否满足种群变异的指标，若是，则进行变异操作，否则进行步骤14，具体方法如下：

13.1判断是否满足种群变异条件，判断方法如下：

judge＝con·dis

13.2种群变异操作步骤如下：

13.2.1设定种群变异迭代次数nmute，种群更新过程中，计算judge参数，判断其是否在nmute次迭代更新中未发生变化，若是则进行步骤13.2.2，否则放弃变异操作；

13.2.2设定种群变异的重构规模nrebuild，并判断当前种群中受支配粒子数ndominate；

13.2.3若ndominate≥nrebuild，则在当前种群的所有受支配粒子中选择nrebuild个并删除，否则，进行步骤13.2.4；

13.2.4若ndominate＜nrebuild，则删除当前种群中所有受支配粒子，并在所有非支配粒子中随机选择(nrebuild-ndominate)个进行删除；

13.2.5按步骤2重新构建nrebuild个粒子，恢复种群规模；

步骤14，使当前代数step增加1，返回步骤6。

本发明的有益效果是：提出了一种基于多目标量子粒子群算法的无人机协同任务分配方法，建立了无人机协同任务分配的模型，将无人机协同任务分配问题中的目标前期任务执行成功概率、无人机生存概率以及任务完成时间这三种指标分别作为多目标任务分配问题的优化目标函数，实现了这三种指标的同时优化。本发明针对无人机协同任务分配的问题的特点，设计了针对前期任务约束的修复算子和针对任务时序约束的修复算子，提高了种群中解的质量，设计了新的种群变异机制，有效提高了算法的收敛速度。

附图说明

图1为算法的编码方式示意图；

图2为非支配解分布图；

图3为f1最优值迭代图；

图4为f2最优值迭代图；

图5为f3最优值迭代图；

图6为本发明的实现方法流程图。

具体实施方式

下面结合附图和实施例对本发明进一步说明，本发明包括但不仅限于下述实施例。

本发明包括步骤如下：

步骤1：输入无人机和任务相关信息，确定算法相关参数。具体内容如下：

输入无人机数量nv；任务目标数量nt；任务目标坐标位置post＝[post1,…,postnt]，其中post1代表第一个目标的坐标，其余类似；无人机速度vuav，vuav为定值，即无人机匀速飞行；无人机初始坐标位置posu＝[posu1,…,posunv]，其中posu1代表第一架无人机初始坐标位置，其余类似；无人机初始种群的规模p。

步骤2：根据双层编码规则生成多个初始种群，具体内容如下：

2.1双层编码规则如下：编码code可表示为code＝[x1,…,xnv,y1,…,ynt]，其中x代表前期任务层编码，x1代表前期任务层第一个编码，其余类似，前期任务层编码共nv维，且均是在[0,nt]内的整数，若为0则代表不进行前期任务。y所代表的是评估任务层，y1代表评估任务层第一个编码，其余类似，评估任务层共nt维，且均是在(1,nv+1)内的实数，实数的整数位是执行对应目标任务的无人机序号，整数相同的基因位实数的小数位大小代表对目标的执行顺序。

2.2种群初始化方法如下：采用kent混沌映射对种群初始化，kent混沌映射公式见下式：

其中，r代表所产生的随机数序列，r^k代表序列中的第k个数，α为实数，一般可取α＝0.4。

在初始化种群时，首先采用kent映射产生分布在[0,1]的随机数序列，然后通过解的取值范围将随机数序列转为个体解。第s个个体的初始解的产生如下所示：

xs1＝round(xmin+r^s(xmax-xmin))

ys1＝ymin+r^s(ymax-ymin)

其中，xs1代表第s个个体的前期任务层的第1个编码，ys1代表第s个个体的评估任务层的第1个编码，其余类似；xmin＝0，xmax＝nt，ymin＝1，ymax＝nv+1；round代表四舍五入。

步骤3：计算所有个体的适应度函数fitness，具体计算方法如下：

3.1计算目标前期任务执行成功概率指标

无人机对目标执行的前期任务可以有多种，例如探测、识别、干扰和搜索。因此，目标前期任务执行成功概率可以为无人机对目标执行探测、识别、干扰和搜索任务中的任一种任务的成功概率，在本发明中将这些任务统称为前期任务。

设无人机对目标前期任务执行成功概率矩阵为pd，pd可以表示为：

其中pd11表示第1架无人机对第1个目标前期任务执行成功概率，其余类似。

假设第i架无人机ui所携带任务载荷对第j个目标tj的任务执行成功概率是pdij。如果对于目标tj只有无人机ui对其进行前期任务，那么对于目标tj的任务执行成功概率pdj如下所示：

pdj＝pdij

如果对于目标tj分配nj架无人机执行任务，则其前期任务执行成功概率pdj如下所示：

那么，多无人机协同任务分配的目标前期任务执行成功概率指标fpd如下所示：

其中，pj表示对第j个目标的最小前期任务执行成功概率要求。

3.2计算无人机生存概率指标

设无人机生存概率矩阵为ps，ps可表示为：

其中ps11表示第1架无人机对第1个目标执行任务的生存概率，其余类似。

假设第i架无人机ui在对第j个目标tj执行任务时的生存概率是psij。如果ui对目标执行任务是在目标确定生存的情况时，ui的生存概率psi如下所示：

psi＝psij

如果对目标执行评估任务，即目标已经被执行前期任务，那么ui的生存概率计算如下所示：

psi＝psij(1-pdj)+pdj

那么，多无人机协同任务分配的无人机生存概率指标表示如下所示：

3.3计算任务完成时间

如果第i架无人机ui完成自身所分配的任务时间为ti，那么，任务完成时间ftime表示如下所示：

3.4计算个体适应度fitness

fitness由关于目标前期任务执行成功概率指标f1，关于无人机生存概率的指标f2以及关于任务完成时间的指标f3组成，即fitness＝[f1,f2,f3]，所使用的无人机协同任务分配模型如下：

其中k根据ftime的大小进行取值，若ftime∈[0,10)则k取1，若ftime∈[10,100)则k取10，若ftime∈[100,1000)则k取100，以此类推；constrains为个体违背约束的个数，对于个体，其应满足以下约束条件，即：

约束1：

约束2：

约束3：t(tj(a))＜t(tj(v)),j＝1,2,...,nt

约束4：pdj≥pj,j＝1,2,...,nt

约束5：

约束6：

约束7：

其中，用表示无人机ui是否对目标tj执行前期任务，若则表示执行，若值为0，则表示不执行；用表示无人机ui是否对目标tj执行评估任务，若则表示执行，若值为0，则表示不执行；t(tj(a))和t(tj(v))分别表示对第j个目标执行前期任务和评估任务的时间；

步骤4：计算当前种群的所有非支配解，并用所有非支配解构成外部种群np，外部种群np的规模为n。

步骤5：将初始种群内第w个个体本身作为其最优解xpbest,w，w＝1,2,…,p，根据非支配解距原点的距离越近越优秀的原则，采用轮盘赌方法进行选择，确定群体最优xgbest。

步骤6：判断当前迭代次数step是否等于最大迭代次数maxstep，若step＝maxstep则停止算法，输出外部种群np作为问题最终的解；若step≠maxstep则继续执行下面的步骤。

步骤7：根据量子粒子群优化算法，更新全部粒子，具体更新方法如下：

根据量子粒子群优化算法，其具体更新公式如下：

其中，和u都是在(0,1)的随机数。代表第r次迭代的粒子w的个体极值的第d维；

代表第r次迭代的群体极值的第d维；代表第r+1次迭代的粒子w的第d维，其余类似；β是惯性权值，其计算方法如下：

步骤8：对粒子采用修复算子进行修复，并按步骤3计算各粒子的适应度，具体方法如下：

8.1针对前期任务约束的修复算子

该算子主要针对存有目标未被分配前期任务的解，对其进行修复，使解能够尽可能满足前期任务约束或降低违背程度。具体操作步骤如下：

8.1.1：判断粒子编码所代表的任务分配结果中的目标是否全被执行前期任务，若是则结束修复进行8.2，否则进行8.1.2；

8.1.2：确定粒子编码所代表的任务分配结果中未被执行前期任务的目标序号tq以及被指派无人机最多的目标tp，其对应无人机有up1,up2,...,upn，n为分配到tp的无人机数量；

8.1.3：判断编码所代表的任务分配结果中是否有未分配前期任务的无人机，若有，假设无人机u01,u02,...,u0m未分配前期任务，m为未分配前期任务的无人机数量，则在u01,u02,...,u0m中，以对目标tq前期任务执行成功概率越高越好为原则，采用轮盘赌的方式选择一架无人机去对tq执行前期任务，结束修复并进行8.2。否则进行8.1.4；

8.1.4：在分配至目标tp的无人机up1,up2,...,upn中，以对目标tp前期任务执行成功概率越低越好为原则，采用轮盘赌的方式选择一架无人机对tq执行前期任务，结束修复并进行8.2。

8.2针对任务时序约束的修复算子

对于无人机执行任务的时序约束需要分两部分进行，首先是确保单机不能在同一目标上执行多次任务，其次是确保同一目标上两类任务的执行次序。具体操作步骤如下：

8.2.1：判断粒子编码所代表的任务分配结果中是否有无人机被分配执行同一目标ti上的前期任务和评估任务，若有则进行8.2.2，否则进行8.2.3；

8.2.2：保持被分配执行同一目标ti上的前期任务和评估任务的无人机所执行的前期任务目标不变，并将在该前期任务目标上执行评估任务的无人机随机改为其他无人机；

8.2.3：确定存有时序冲突的目标ti，并计算前期任务层结束后各机(除对目标ti进行前期任务的无人机)前往目标ti的累计航行距离；

8.2.4：以离ti的累计航行距离越大越好为原则，采用轮盘赌的方式选取一架无人机对目标ti进行评估；

8.2.5：计算修复后粒子的适应度fitness′，若修复后粒子适应度fitness′小于未修复之前的适应度则保留，否则维持原粒子编码不变。

步骤9：判断当前种群个体是否支配个体极值，即x′w＞xpbest，w，其中x′w代表当前种群第w个个体，若支配个体极值，则令xpbest,w＝x′w，否则维持xpbest,w不变。

步骤10：将迭代产生的新解与外部种群的解进行比较，根据算法中的外部种群添加策略判断是否将新解加入外部种群，外部种群添加策略如下：

第e个粒子经过迭代更新后为xe，迭代过程中的外部种群np＝(xnp1,xnp2,...,xnpn)，将xe与np中的非支配解进行比较，添加策略为：若存在xnps＞xe，s＝1，2，...，n，那么维持np不变；若xe＞xnps，则将xnps从np中删除，并添加xe进入np，这里的xnps可以是多个；否则，直接添加xe进入np。

步骤11：若外部种群np规模超出设定值，从拥挤距离最小的粒子进行裁剪，直至恢复外部种群规模，以保持所设定的规模n，第e个粒子的拥挤距离计算公式如下：

dcrowde＝dcrowde,1+dcrowde,2+dcrowde,3

其中，f1,e-1为f1的第e-1个数的值，e＞1且e＜|f1|，|f1|为f1中数据的个数，且f1,e-1＜f1,e＜f1,e+1，f1,max为f1中最大的数，f1,min为f1中最小的数，其余类似；当e＝1或e＝|f1|时，dcrowde,1＝∞，其余类似。

步骤12：将当前外部种群中最优粒子作为群体最优粒子xgbest；

步骤13：判断是否满足种群变异的指标，若是，则进行变异操作，否则进行步骤14，具体方法如下：

13.1判断是否满足种群变异条件，判断方法如下：

judge＝con·dis

con＝(minf1)²+(minf2)²+(minf3)²

13.2种群变异操作步骤如下：

13.2.1：设定种群变异迭代次数nmute，种群更新过程中，计算judge参数，判断其是否在nmute次迭代更新中未发生变化，若是则进行13.2.2，否则放弃变异操作；

13.2.2：设定种群变异的重构规模nrebuild，并判断当前种群中受支配粒子数ndominate；

13.2.3：若ndominate≥nrebuild，则在当前种群的所有受支配粒子中选择nrebuild个并删除，否则，进行13.2.4；

13.2.4：若ndominate＜nrebuild，则删除当前种群中所有受支配粒子，并在所有非支配粒子中随机选择(nrebuild-ndominate)个进行删除；

13.2.5：按步骤2重新构建nrebuild个粒子，恢复种群规模

步骤14：使得当前代数step增加1，返回步骤6。

本发明的实施例按照图6所示的流程图实施如下步骤：

步骤1：输入无人机和任务相关信息，确定算法相关参数。具体内容如下：

输入无人机数量nv；任务目标数量nt；任务目标坐标位置post＝[post1,…,postnt]，其中post1代表第一个目标的坐标，其余类似；无人机速度vuav，vuav为定值，即无人机匀速飞行；无人机初始坐标位置posu＝[posu1,…,posunv]，其中posu1代表第一架无人机初始坐标位置，其余类似；无人机初始种群的规模p。

步骤2：根据双层编码规则生成多个初始种群，具体内容如下：

2.1双层编码规则如下：编码code可表示为code＝[x1,…,xnv,y1,…,ynt]，其中x代表前期任务层编码，x1代表前期任务层第一个编码，其余类似，前期任务层编码共nv维，且均是在[0,nt]内的整数，若为0则代表不进行前期任务。y所代表的是评估任务层，y1代表评估任务层第一个编码，其余类似，评估任务层共nt维，且均是在(1,nv+1)内的实数，实数的整数位是执行对应目标任务的无人机序号，整数相同的基因位实数的小数位大小代表对目标的执行顺序。图1为编码的示意图，编码前段是前期任务层，后段是评估层。

2.2种群初始化方法如下：采用kent混沌映射对种群初始化，kent混沌映射公式见下式：

其中，r代表所产生的随机数序列，r^k代表序列中的第k个数，α为实数，一般可取α＝0.4。

在初始化种群时，首先采用kent映射产生分布在[0,1]的随机数序列，然后通过解的取值范围将随机数序列转为个体解。第s个个体的初始解的产生如下所示：

xs1＝round(xmin+r^s(xmax-xmin))

ys1＝ymin+r^s(ymax-ymin)

其中，xs1代表第s个个体的前期任务层的第1个编码，ys1代表第s个个体的评估任务层的第1个编码，其余类似；xmin＝0，xmax＝nt，ymin＝1，ymax＝nv+1；round代表四舍五入。

步骤3：计算所有个体的适应度函数fitness，具体计算方法如下：

3.1计算目标前期任务执行成功概率指标

无人机对目标执行的前期任务可以有多种，例如探测、识别、干扰和搜索。因此，目标前期任务执行成功概率可以为无人机对目标执行探测、识别、干扰和搜索任务中的任一种任务的成功概率，在本发明中将这些任务统称为前期任务。

设无人机对目标前期任务执行成功概率矩阵为pd，pd可以表示为：

其中pd11表示第1架无人机对第1个目标前期任务执行成功概率，其余类似。

假设第i架无人机ui所携带任务载荷对第j个目标tj的任务执行成功概率是pdij。如果对于目标tj只有无人机ui对其进行前期任务，那么对于目标tj的任务执行成功概率pdj如下所示：

pdj＝pdij

如果对于目标tj分配nj架无人机执行任务，则其前期任务执行成功概率pdj如下所示：

那么，多无人机协同任务分配的目标前期任务执行成功概率指标fpd如下所示：

其中，pj表示对第j个目标的最小前期任务执行成功概率要求。

3.2计算无人机生存概率指标

设无人机生存概率矩阵为ps，ps可表示为：

其中ps11表示第1架无人机对第1个目标执行任务的生存概率，其余类似。

假设第i架无人机ui在对第j个目标tj执行任务时的生存概率是psij。如果ui对目标执行任务是在目标确定生存的情况时，ui的生存概率psi如下所示：

psi＝psij

如果对目标执行评估任务，即目标已经被执行前期任务，那么ui的生存概率计算如下所示：

psi＝psij(1-pdj)+pdj

那么，多无人机协同任务分配的无人机生存概率指标表示如下所示：

3.3计算任务完成时间

如果第i架无人机ui完成自身所分配的任务时间为ti，那么，任务完成时间ftime表示如下所示：

3.4计算个体适应度fitness

fitness由关于目标前期任务执行成功概率指标f1，关于无人机生存概率的指标f2以及关于任务完成时间的指标f3组成，即fitness＝[f1,f2,f3]，所使用的无人机协同任务分配模型如下：

其中k根据ftime的大小进行取值，若ftime∈[0,10)则k取1，若ftime∈[10,100)则k取10，若ftime∈[100,1000)则k取100，以此类推；constrains为个体违背约束的个数，对于个体，其应满足以下约束条件，即：

约束1：

约束2：

约束3：t(tj(a))＜t(tj(v)),j＝1,2,...,nt

约束4：pdj≥pj,j＝1,2,...,nt

约束5：

约束6：

约束7：

其中，用表示无人机ui是否对目标tj执行前期任务，若则表示执行，若值为0，则表示不执行；用表示无人机ui是否对目标tj执行评估任务，若则表示执行，若值为0，则表示不执行；t(tj(a))和t(tj(v))分别表示对第j个目标执行前期任务和评估任务的时间；

约束1和约束2表示目标所需执行任务类型约束，每个目标上需要执行的任务类型有前期任务和评估任务两种，并且每个目标上的两种任务类型都需要被执行，约束1表示对每个目标都要进行前期任务并且对于同一目标可以多架无人机进行协同前期任务，约束2表示对每个目标都要进行评估且仅评估一次。约束3表示任务执行时序约束，即在同一目标上，前期任务需在评估任务之前进行。约束4表示最小前期任务成功概率约束，即对于每一个目标前期任务执行成功概率均需高于所要求的最小值，以实现作战的可靠性。约束5，约束6，约束7表示无人机自身性能约束，约束5表示单机只能执行一次前期任务，约束6表示每架无人机可以执行多次评估任务，约束7表示每架无人机在一个目标上最多只能执行一次任务。

步骤4：计算当前种群的所有非支配解，并用所有非支配解构成外部种群np，外部种群np的规模为n。

步骤5：将初始种群内第w个个体本身作为其最优解xpbest,w，w＝1,2,…,p，根据非支配解距原点的距离越近越优秀的原则，采用轮盘赌方法进行选择，确定群体最优xgbest。

步骤6：判断当前迭代次数step是否等于最大迭代次数maxstep，若step＝maxstep则停止算法，输出外部种群np作为问题最终的解；若step≠maxstep则继续执行下面的步骤。

步骤7：根据量子粒子群优化算法，更新全部粒子，具体更新方法如下：

根据量子粒子群优化算法，其具体更新公式如下：

其中，和u都是在(0,1)的随机数。代表第r次迭代的粒子w的个体极值的第d维；

代表第r次迭代的群体极值的第d维；代表第r+1次迭代的粒子w的第d维，其余类似；β是惯性权值，其计算方法如下：

步骤8：对粒子采用修复算子进行修复，并按步骤3计算各粒子的适应度，具体方法如下：

8.1针对前期任务约束的修复算子

该算子主要针对存有目标未被分配前期任务的解，对其进行修复，使解能够尽可能满足前期任务约束或降低违背程度。具体操作步骤如下：

8.1.1：判断粒子编码所代表的任务分配结果中的目标是否全被执行前期任务，若是则结束修复进行8.2，否则进行8.1.2；

8.1.2：确定粒子编码所代表的任务分配结果中未被执行前期任务的目标序号tq以及被指派无人机最多的目标tp，其对应无人机有up1,up2,...,upn，n为分配到tp的无人机数量；

8.1.3：判断编码所代表的任务分配结果中是否有未分配前期任务的无人机，若有，假设无人机u01,u02,...,u0m未分配前期任务，m为未分配前期任务的无人机数量，则在u01,u02,...,u0m中，以对目标tq前期任务执行成功概率越高越好为原则，采用轮盘赌的方式选择一架无人机去对tq执行前期任务，结束修复并进行8.2。否则进行8.1.4；

8.1.4：在分配至目标tp的无人机up1,up2,...,upn中，以对目标tp前期任务执行成功概率越低越好为原则，采用轮盘赌的方式选择一架无人机对tq执行前期任务，结束修复并进行8.2。

8.2针对任务时序约束的修复算子

对于无人机执行任务的时序约束需要分两部分进行，首先是确保单机不能在同一目标上执行多次任务，其次是确保同一目标上两类任务的执行次序。具体操作步骤如下：

8.2.1：判断粒子编码所代表的任务分配结果中是否有无人机被分配执行同一目标ti上的前期任务和评估任务，若有则进行8.2.2，否则进行8.2.3；

8.2.2：保持被分配执行同一目标ti上的前期任务和评估任务的无人机所执行的前期任务目标不变，并将在该前期任务目标上执行评估任务的无人机随机改为其他无人机；

8.2.3：确定存有时序冲突的目标ti，并计算前期任务层结束后各机(除对目标ti进行前期任务的无人机)前往目标ti的累计航行距离；

8.2.4：以离ti的累计航行距离越大越好为原则，采用轮盘赌的方式选取一架无人机对目标ti进行评估；

8.2.5：计算修复后粒子的适应度fitness′，若修复后粒子适应度fitness′小于未修复之前的适应度则保留，否则维持原粒子编码不变。

步骤9：判断当前种群个体是否支配个体极值，即x′wxpbest，w，其中x′w代表当前种群第w个个体，若支配个体极值，则令xpbest,w＝x′w，否则维持xpbest,w不变。

步骤10：将迭代产生的新解与外部种群的解进行比较，根据算法中的外部种群添加策略判断是否将新解加入外部种群，外部种群添加策略如下：

第e个粒子经过迭代更新后为xe，迭代过程中的外部种群np＝(xnp1,xnp2,...,xnpn)，将xe与np中的非支配解进行比较，添加策略为：若存在xnps＞xe，s＝1，2，...，n，那么维持np不变；若xe＞xnps则将xnps从np中删除，并添加xe进入np，这里的xnps可以是多个；否则，直接添加xe进入np。

步骤11：若外部种群np规模超出设定值，从拥挤距离最小的粒子进行裁剪，直至恢复外部种群规模，以保持所设定的规模n，第e个粒子的拥挤距离计算公式如下：

dcrowde＝dcrowde,1+dcrowde,2+dcrowde,3

其中，f1,e-1为f1的第e-1个数的值，e＞1且e＜|f1|，|f1|为f1中数据的个数，且f1,e-1＜f1,e＜f1,e+1，f1,max为f1中最大的数，f1,min为f1中最小的数，其余类似；当e＝1或e＝|f1|时，dcrowde,1＝∞，其余类似。

步骤12：将当前外部种群中最优粒子作为群体最优粒子xgbest；

步骤13：判断是否满足种群变异的指标，若是，则进行变异操作，否则进行步骤14，具体方法如下：

13.1判断是否满足种群变异条件，判断方法如下：

judge＝con·dis

con＝(minf1)²+(minf2)²+(minf3)²

13.2种群变异操作步骤如下：

13.2.1：设定种群变异迭代次数nmute，种群更新过程中，计算judge参数，判断其是否在nmute次迭代更新中未发生变化，若是则进行13.2.2，否则放弃变异操作；

13.2.2：设定种群变异的重构规模nrebuild，并判断当前种群中受支配粒子数ndominate；

13.2.3：若ndominate≥rebnuild，则在当前种群的所有受支配粒子中选择nrebuild个并删除，否则，进行13.2.4；

13.2.4：若ndominate＜nrebuild，则删除当前种群中所有受支配粒子，并在所有非支配粒子中随机选择(nrebuild-ndominate)个进行删除；

13.2.5：按步骤2重新构建nrebuild个粒子，恢复种群规模

步骤14：使得当前代数step增加1，返回步骤6。

本发明的效果可以通过以下仿真实例进一步说明：

仿真中，任务执行区域设定为我方出动8架无人机对4个目标，对每个目标均需执行前期任务和评估两种任务，我方无人机均具备综合任务执行能力，即两种任务类型均可以执行，且我方8架无人机分布于3个位置不同的无人机发射平台上，每架无人机携带1个前期任务资源且所有无人机的速度是一致的。无人机平台和目标的信息见表1和表2。

表1无人机平台信息

表2目标信息

所设定的各无人机对不同目标前期任务执行成功概率和对目标进行任务时无人机自身生存概率的情况见表3和表4。

表3无人机对目标前期任务概率

表4无人机生存概率

算法的相关参数为：种群规模p＝10，外部种群np的规模n＝10，算法共进行迭代300次，个体变异pm＝0.1，种群变异条件为20代内指标未发生变化则进行变异，变异规模为种群规模的1/5。

实例1：假设4架无人机对2个目标进行任务，对其进行任务分配。根据排列组合知识可得对这一简单问题共有1620种分配方案，采用穷举法得出全部分配方案并进行比较计算，可得在这1620种方案中只有5个是非支配解，这5个解也就构成了这一问题的pareto前端，5个解对应的分配方案如表5左半部分所示。而通过本发明算法最终也输出了5个解，这5个解与穷举法所得结果完全一致，如表5右半部分所示。同样，4架无人机对3个目标作战时，通过穷举法得到30720种方案，其中有13个非支配解，本发明算法同样可以全部找出pareto前端解。因此本发明算法具有较好的收敛性。

表5所得结果对比

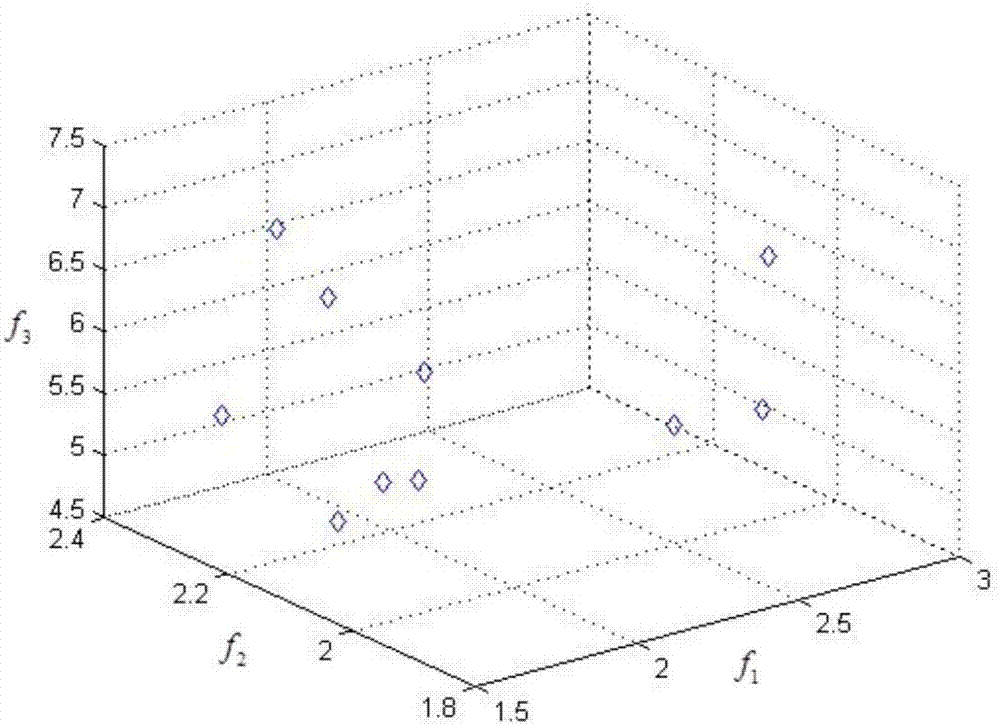
实例2：采用基于多目标量子粒子群算法的协同任务分配方法对设定任务场景问题求解所得的结果如图2，其表示所求得问题非支配解在目标空间中的分布。

图3、图4、图5分别给出了更新过程中3个目标函数最优值的迭代图。由图可以看出，随着粒子的更新迭代，3个目标函数均得到了优化，最后收敛到一个稳定值，稳定值分别对应着对3个目标函数最终的最优解。由图2可以看出，算法输出的外部种群中的非支配解分布分散，种群多样性得到了保证，因此，算法对于问题的求解是有效的。