基于加权下推系统的中断验证系统的制作方法

本发明属于程序的静态分析以及模型检验领域,涉及一种基于加权下推系统的中断验证技术。

背景技术：

随着计算机和移动互联网的飞速发展，嵌入式实时系统被广泛应用于各个行业：制造、医疗、交通以及通信等各个行业都与嵌入式实时系统有着密切联系。相对于普通计算机系统，嵌入式实时系统对于可靠性有着更高的要求，特别当一个实时系统应用在关乎生命的领域时，任何不可靠因素或某些强实时任务超过规定时限，都可能引起难以预测的严重后果。在嵌入式实时系统中，为了使系统可以及时地与外界环境进行交互，人们引入了“中断机制”：中断是实时系统的一个重要部分，当出现需求时，它使得处理器可以暂时停止当前程序的执行转而去执行处理新情况的程序。然而，中断产生的随机性和不确定会对系统的内存安全和时间安全等方面产生不小的隐患。而通过形式化方法的技术对中断的相关性质进行研究验证，不仅保证了中断机制的正常运行，而且还能提高此类系统的安全性指标。

目前国内外对于此问题已有一些验证方法，但是都无法用同一个方法来验证有关中断的重要问题，比如使用中断时间自动机(interrupttimedautomata,ita)来描述带有中断的多任务系统，将实时系统转换为中断时间自动机，通过对ita进行可达性分析来验证系统是否满足某种或某几种性质，但是当系统过于庞大时，所转成的中断时间自动机会产生状态爆炸等相关问题；通过加颜色的控制流图,用来对中断驱动的软件进行静态检查，其主要针对栈的长度和类型以及执行时间的deadline进行分析。以及通过抽象中断机(theabstractinterruptmachine,aim)，将程序抽象到线程一层，将同步操作看作原子操作，使用抽象中断机来描述程序中断处理与顺序非处理代码之前的交互，通过程序逻辑中的规范语言来判断是否存在中断所产生的相关问题，通过aim可以解决共享资源访问冲突以及中断造成的堆栈、内存溢出等问题。

技术实现要素：

针对以上问题，本发明的目的是提供基于加权下推系统的中断验证系统，将程序目标代码转换为加权下推系统，求出加权下推系统的可达格局，继而根据可达格局对程序进行分析，针对求出的可达格局对时序逻辑、优先级反转、内存访问冲突以及超时问题进行验证。

为实现以上目的，并解决有中断驱动的嵌入式实时系统中存在的几类问题，本发明采取的技术方案是：一种基于加权下推系统的中断验证系统，包括：

目标代码建模模块：其用于提取需要验证的不同任务的程序的目标代码，将其转换为加权下推系统；

可达格局获得模块：其用于根据所述加权下推系统的可达性算法以及问题的需求计算出pre加权自动机或post加权自动机，pre加权自动机或post加权自动机可接受的语言作为可达格局；

可达格局遍历模块：其用于遍历获得的所有的可达格局，在遍历的过程中，判断当前格局信息是否满足验证需求性质，如果不满足，判读错误类型，跳转至当前格局回溯模块，若遍历完所有格局均满足验证需求性质，返回正确，则跳转至结果输出模块；

当前格局回溯模块：其用于根据当前格局进行回溯，找出不满足所需验证性质的路径，给出该程序不满足验证需求性质的结果，并且给出反例路径，算法结束；

结果输出模块：其用于给出所述程序满足验证需求性质的结果。

优选地，所述加权下推系统包括三元组w＝(p,s,f)，其中p＝(p,γ,δ)为下推系统，为有界幂等半环，f：δ→d是将下推规则映射到权重。

优选地，所述下推系统p＝(p,γ,δ)中，p是有限的控制位置集合，γ是有限的栈字符集合，δ是有限的迁移规则的集合规则的形式为：<p,v→q,w>，其中，(p,v,q,w)∈δ。

优选地，所述有界幂等半环中，d为权重集，0，1∈d，为d上的二元操作：

1)(d,)为以0为中性元的可交换的幺半群，并且是幂等的；

2)(d，)为以1为中性元的幺半群；

3)对可分配，即对于所有a,b,c∈d，有

4)0为操作的零化子，即对于所有a∈d，

5)d上偏序关系＜定义为b∈d,a＜b当且仅当a⊕b＝a,在此关系下不存在无穷降链。

优选地，所述可达性包括给定一个初始格局和一个目标格局，判断能否从初始格局出发，通过有限步的格局迁移到达目标格局。

优选地,所述pre加权自动机为接受所有从当前格局可以到达的所有pre可达格局的自动机，所有pre可达格局为所有可以通过有限步的格局迁移到达该格局的格局集合。

优选地,所述post加权自动机为接受所有从当前格局可以到达的所有post可达格局的自动机，所有post可达格局为该格局通过有限步的格局迁移可以到达的格局集合。

优选地，所述的验证需求性质包括：1.程序运行时是否满足规定的时序逻辑；2.程序是否会出现因中断产生优先级反转的情况，即优先级低的任务可以打断优先级高的任务及其子任务；3.程序运行是否满足实时性，即能够在规定的时间内完成某项任务；4.程序运行时是否有因为中断产生的内存访问冲突。

本发明的有益效果包括：

1.将实时系统的中断验证与加权下推系统相结合，以形式化的方式对实时系统中断进行验证，提高了验证的可靠性和鲁棒性。

2.同一个模型下同时验证有关中断的时序逻辑、优先级反转、内存访问冲突以及超时问题，具有高效性，同时也节约了成本。

附图说明

图1是本发明基于加权下推系统的中断验证方法的框架图；

图2是本发明基于加权下推系统的中断验证方法的步骤图；

图3是本发明中求解pre自动机的算法图；

图4是本发明中求解post自动机的算法图；

图5是应用本发明基于加权下推系统的中断验证方法验证超时问题的框架图。

图6是基于加权下推系统的中断验证系统的框架图。

具体实施方式

结合以下具体附图，对本发明作进一步的详细说明。实施本发明的过程、条件等，除以下专门提及的内容之外，均为本领域的普遍知识和公知常识，本发明没有特别限制内容。

本发明的目的是将嵌入式实时系统的中断验证与加权下推系统相结合，将实时系统的目标代码建模成加权下推系统模型，将所需信息加入到模型中，在同一个模型下同时验证有关中断的几类重要问题。

本发明公开了一种基于加权下推系统的中断验证方法，该方法采用加权下推系统来表示嵌入式实时系统中有关中断的目标代码之间的跳转关系，通过对目标代码建模成的加权下推系统进行可达性分析，从而判断系统的中断是否满足安全性与可靠性。

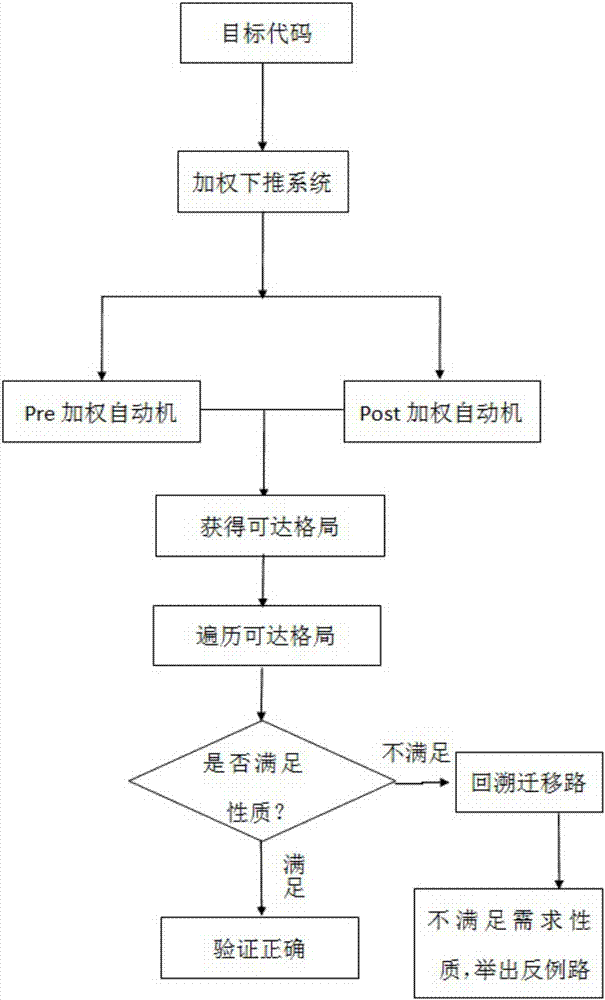
如图1所示，本方明的基于加权下推系统的中断验证方法包括：首先根据程序目标代码中指令的跳转关系将其建模成加权下推系统，在这个过程中，将优先级信息压入一个堆栈，将指令周期信息作为权值，然后通过加权下推系统的可达性算法，得出所有的可达格局；最后遍历所得的可达格局，判断当前格局信息是否满足需求，如果不满足，则判断错误类型，返回错误路径，若遍历完所有可达格局没有发现错误，则返回正确。

如图2所示，本发明提出的所述基于加权下推系统的中断验证方法，具体步骤为：

步骤1：提取需要验证的程序的目标代码，将其转换为加权下推系统；优选地，在该步骤中，提取需要验证的不同任务的程序的目标代码，为所述不同任务的程序的目标代码分别添加优先级信息以及指令周期信息，即将优先级信息压入一个堆栈，将指令周期信息作为权值，根据所述程序目标代码中指令的跳转关系将所述目标代码建模成加权下推系统；

步骤2：根据加权下推系统的可达性算法以及问题的需求计算出pre加权自动机或post加权自动机，加权自动机可接受的语言构成可达格局；

步骤3：遍历步骤2获得的可达格局，在遍历的过程中，判断所遍历的格局是否满足所需验证的性质，若不满足，则进行步骤4，若遍历完全后所有格局均满足性质，则进行步骤5；

步骤4：根据当前格局进行回溯，找出不满足所需验证性质的路径，给出该程序不满足需求性质的结果，并且给出反例路径，算法结束；

步骤5：给出该程序满足需求性质的结果。

所述下推系统为p＝(p,γ,δ)中，p是有限的控制位置集合，γ是有限的栈字符集合，δ是有限的迁移规则的集合规则的形式为：<p,v→q,w>，其中，(p,v,q,w)∈δ。

所述有界幂等半环为中，d为权重集，0，1∈d，为d上的二元操作：

1)(d,)为以0为中性元的可交换的幺半群，并且是幂等的(例如，对于所有的a∈d，)；

2)(d，)为以1为中性元的幺半群；

3)对可分配，即对于所有a,b,c∈d，有

4)0为操作的零化子，即对于所有a∈d，

5)d上偏序关系＜定义为b∈d,a＜b当且仅当在此关系下不存在无穷降链。

所述可达性定义为给定一个初始格局和一个目标格局，判断能否从初始格局出发，通过有限步的格局迁移到达目标格局。

所述pre加权自动机为接受所有从当前格局可以到达的所有pre可达格局的自动机。

所述pre可达格局定义为所有可以通过有限步的格局迁移到达该格局的格局集合。

如图3所示，本发明提出的所述基于加权下推系统的中断验证方法中，所述pre加权自动机的求解方法包括以下步骤：

1.输入加权系统w＝(p，s，f)，其中p＝(p,γ,δ)，以及可以接受初始格局集合c的自动机a＝(q,γ,→0，p，f)；

2.初始化→:＝→0；workset:＝→0；l:＝λt.0，其中λt.0表示s中零元；对于所有t∈→0，对l(t):＝1,对于δ中所有规则做update(p,γ,p’),f(r))；

3.检查workset是否为空，如果为空，则进行步骤5，否则进行步骤4；

4.从workset中选择一条迁移t＝(q,γ,q’)，并将其移出workset，对δ中所有规则为做update((p1,γ1,q’),)；对δ中所有规则为中的所有t’＝(q’,γ2,q”)∈→做update((p1,γ1,q”),)；对于δ中所有规则为中满足t’＝(p’,γ2,q)∈→做update((p1,γ1,q’),)，返回步骤3；

5.返回pre加权自动机a＝(q,γ,→0，p，f)。

所述post加权自动机为接受所有从当前格局可以到达的所有post可达格局的自动机。

所述post可达格局定义为该格局通过有限步的格局迁移可以到达的格局集合。

如图4所示，本发明提出的所述基于加权下推系统的中断验证方法中，所述post加权自动机的求解方法包括以下步骤：

所述的验证性质为：1.程序运行时是否满足规定的时序逻辑；2.程序是否会出现因中断产生优先级反转的情况，即优先级低的任务可以打断优先级高的任务及其子任务；3.程序运行是否满足实时性，即能够在规定的时间内完成某项任务；4.程序运行时是否有因为中断产生的内存访问冲突。

下面具体讲述本发明所述基于加权下推系统的中断验证方法。

实施例1

本实施例是以应用本发明基于加权下推系统的中断验证方法验证目标代码超时问题为例。

图5是应用本发明基于加权下推系统的中断验证方法验证超时问题的框架图。验证的具体步骤为：

1.根据需要验证的目标代码，将其转换为跨过程控制流图(interproceduralcontrolgraph,icfg)；

2.求出icfg中每个循环的最小上界，当转换为wpds时，对该循环做最小上界次的权值运算；

3.根据需要验证的目标代码，将其指令周期作为权值，将有界幂等半环中

运算符定义为取最小值，将运算符定义为算数加法，将幺元1定义为无穷，将零元0定义为整数1；

4.根据步骤1，2，3所求的信息得出加权下推系统；

5.根据图4的算法求出加权下推系统的post加权自动机，并根据其得出所有可达格局；

6.根据可达格局，求出所需路径的权值，即用本发明所述基于加权下推系统的中断验证方法求出的目标代码运行时间；

7.判断所求目标代码运行时间是否小于规定时间，如果小于，则进行步骤8，否则进行步骤9；

8.系统未超时，返回满足验证要求。

9.系统超时，回溯迁移路径，返回反例路径。

此外，如图6所示,本发明还公开一种基于加权下推系统的中断验证系统，包括：

目标代码建模模块：其用于提取需要验证的不同任务的程序的目标代码，将其转换为加权下推系统；

可达格局获得模块：其用于根据所述加权下推系统的可达性算法以及问题的需求计算出pre加权自动机或post加权自动机，pre加权自动机或post加权自动机可接受的语言作为可达格局；

可达格局遍历模块：其用于遍历获得的所有的可达格局，在遍历的过程中，判断当前格局信息是否满足验证需求性质，如果不满足，判读错误类型，跳转至当前格局回溯模块，若遍历完所有格局均满足验证需求性质，返回正确，则跳转至结果输出模块；

当前格局回溯模块：其用于根据当前格局进行回溯，找出不满足所需验证性质的路径，给出该程序不满足验证需求性质的结果，并且给出反例路径，算法结束；

结果输出模块：其用于给出所述程序满足验证需求性质的结果。

在一种优选实施方式中，目标代码建模模块包括：用于提取需要验证的不同任务的程序的目标代码，为所述不同任务的程序的目标代码分别添加优先级信息以及指令周期信息，根据所述程序目标代码中指令的跳转关系将所述目标代码建模成加权下推系统。

在一种优选实施方式中，可达格局获得模块包括：用于根据所述加权下推系统的可达性算法以及问题的需求计算出pre加权自动机或post加权自动机，并获得所有的可达格局。

在上述的中断验证系统中，所述加权下推系统包括三元组w＝(p,s,f)，其中p＝(p,γ,δ)为下推系统，为有界幂等半环，f：δ→d是将下推规则映射到权重。

所述下推系统p＝(p,γ,δ)中，p是有限的控制位置集合，γ是有限的栈字符集合，δ是有限的迁移规则的集合规则的形式为：<p,v→q,w>，其中，(p,v,q,w)∈δ。

所述有界幂等半环中，d为权重集，0，1∈d，为d上的二元操作：

1)(d,)为以0为中性元的可交换的幺半群，并且是幂等的；

2)(d，)为以1为中性元的幺半群；

3)对可分配，即对于所有a,b,c∈d，有

4)0为操作的零化子，即对于所有a∈d，

5)d上偏序关系＜定义为b∈d,a＜b当且仅当在此关系下不存在无穷降链。

所述可达性包括给定一个初始格局和一个目标格局，判断能否从初始格局出发，通过有限步的格局迁移到达目标格局。

所述pre加权自动机包括接受所有从当前格局可以到达的所有pre可达格局的自动机，所有pre可达格局定义为所有可以通过有限步的格局迁移到达该格局的格局集合。

本发明提出的所述基于加权下推系统的中断验证系统中，所述pre加权自动机的计算求解采用以下模块实现：

模块1.输入加权系统w＝(p，s，f)，其中p＝(p,γ,δ)，以及可以接受初始格局集合c的自动机a＝(q,γ,→0，p，f)；

模块2.初始化→:＝→0；workset:＝→0；l:＝λt.0，其中λt.0表示s中零元；

对于所有t∈→0，对l(t):＝1,对于δ中所有规则做update(p,γ,p’),f(r))；

模块3.检查workset是否为空，如果为空，则进行步骤5，否则进行步骤4；

模块4.从workset中选择一条迁移t＝(q,γ,q’)，并将其移出workset，对δ中所有规则为做update((p1,γ1,q’),)；对δ中所有规则为中的所有t’＝(q’,γ2,q”)∈→做update((p1,γ1,q”),)；对于δ中所有规则为中满足t’＝(p’,γ2,q)∈→做update((p1,γ1,q’),)，返回步骤3；

模块5.返回pre加权自动机a＝(q,γ,→0，p，f)。

所述post加权自动机包括接受所有从当前格局可以到达的所有post可达格局的自动机，所有post可达格局定义为该格局通过有限步的格局迁移可以到达的格局集合。

本发明提出的所述基于加权下推系统的中断验证系统中，所述post加权自动机的计算求解采用以下模块实现：

该系统的验证需求性质包括：1.程序运行时是否满足规定的时序逻辑；2.程序是否会出现因中断产生优先级反转的情况，即优先级低的任务可以打断优先级高的任务及其子任务；3.程序运行是否满足实时性，即能够在规定的时间内完成某项任务；4.程序运行时是否有因为中断产生的内存访问冲突。

应当声明的是，其只是针对本发明可行实施例的具体说明，该实施例并非用以限制本发明的专利范围，本发明应包括，但不仅限于上述详述以及具体例子。本发明应包括核心内容范围内的一切调整及修改，凡未脱离本发明所为的等效实施或变更，均应包含于本案的专利范围中。