一种索桁结构的找形方法与流程

本发明属于建筑工程中的建筑设计和结构设计领域，具体涉及一种索桁结构的找形方法。

背景技术：

索桁结构由一系列索桁架按一定规律排列组合而成，常见的索桁架布置方式有车辐式、平行式、交叉式等。这种结构形式具有自重轻、适用跨度大、施工方便等特点，因而广泛应用于各类大跨度结构、幕墙结构等建筑形式中。

索桁结构的基本组成单元可归纳为上弦索、下弦索和两层拉索之间的撑杆(或吊索)，是一种典型的索杆张力结构体系。这类结构需要通过引入预应力来形成刚度，进而具备承载能力。引入预应力前后的结构状态分别称作零状态和初始态。对索桁结构而言，结构能否形成承载能力与结构构形直接相关，因此找形(formfinding)一直是索桁结构研究和设计中的核心问题之一。目前应用于索桁结构的找形方法主要有非线性有限元法、动力松弛法、力密度法等。索桁结构构形确定后，利用平衡矩阵理论等可以得到结构的预应力分布，并按照结构刚度和承载力要求确定预应力水平，即得到索桁结构的初始态。

在工程实践中，建筑屋面或幕墙通常直接或间接铺设在索桁结构上弦索或下弦索所处的面内。为实现建筑效果，屋面或幕墙几何形状通常由建筑师确定，即索桁架的上弦(或下弦)几何形状给定，同时撑杆(或吊索)一般保持竖直。因此，工程中需要一种能在部分构件几何形状给定时的索桁结构找形方法，从而能在保证建筑效果的前提下找到索桁结构初始态。

技术实现要素：

针对现有技术中存在的问题，本发明的目的在于提供一种索桁结构的找形方法，其有效解决了现有技术中存在的问题。

为实现上述目的，本发明采用以下技术方案：

一种索桁结构的找形方法，所述方法包括如下步骤：

1)建立符合给定屋面或幕墙几何形状的索桁结构上弦或下弦节点，根据拓扑关系连接各节点，得到上弦索或下弦索的几何模型；

2)将各上弦或下弦节点沿竖直方向向下或向上偏移任意距离，得到各下弦或上弦节点的初始位置，连接相应的上、下弦节点得到撑杆或吊索的初始几何模型；

3)约束外环支座节点及撑杆或吊索的下或上端点，得到找力模型，命名为模型a；

4)另建找形模型b：根据步骤2)中下弦或上弦节点的初始位置建立下弦索或上弦索的初始几何模型，并约束外环支座节点；

5)组集模型a的平衡矩阵并进行奇异值分解，得到其自应力模态；

6)将模型a的自应力模态进行线性组合，提取组合结果中撑杆或吊索的对应数值，当自应力模态唯一时，直接提取模态中撑杆或吊索的对应数值，所得结果作为找形时的外荷载；

7)以力密度为变量建立模型b的x向和y向平衡方程组，组集方程组的系数矩阵，称为力密度平衡矩阵，对矩阵进行奇异值分解，得到模型b满足x向和y向平衡条件的力密度模态；

8)将模型b的力密度模态进行线性组合，当力密度模态唯一时，可直接乘以调整系数，所得结果作为找形采用的力密度；

9)采用步骤8)得到的力密度，并将步骤6)得到的外荷载施加到模型b的相应节点，对模型b进行带荷载的力密度法找形，得到满足平衡条件和撑杆或吊索竖直要求的下弦或上弦节点坐标，由于找形过程中各节点的x、y坐标自动满足平衡，可仅更新z坐标，故称之为单方向力密度法；

10)利用模型a中的上弦或下弦节点坐标和找形后模型b中的下弦或上弦节点坐标，建立索桁结构的整体几何模型，命名为模型c；

11)检查模型c的几何尺寸是否满足与建筑功能相关的要求，若满足则进入后续步骤，若不满足则返回步骤8)，更新力密度模态组合系数或调整系数，并重新进行找形，直至得到几何尺寸满足要求的的索桁结构；

12)组集模型c的平衡矩阵并进行奇异值分解，得到找形完成的索桁结构自应力模态；之后考虑自重或其他荷载对找形结果进行修正。

进一步，步骤7)中所述力密度平衡矩阵和力密度模态具体含义及计算方法为：

为模型b的第i个节点建立x向和y向平衡方程：

其中(xi,yi)为第i个节点的x、y坐标，n为连接到第i个节点的单元数量，lk、fk和(xk,yk)(k＝1,2,…,n)分别为连接到第i个节点的第k个单元的长度、内力和另一端点的x、y坐标；引入力密度qk＝fk/lk，可将式(1)变换为：

在式(2)中，(xi,yi)、(xk,yk)已经根据各节点的水平位置给定，而qk未知，因此可以将式(2)视为关于qk的方程组；为模型b所有节点建立同样的平衡方程，组集后写成矩阵形式：

[aq]{q}＝{0}(3)

式(3)中的矩阵[aq]称为模型b的力密度平衡矩阵，{q}为满足模型b各节点水平平衡条件的力密度；

将[aq]进行奇异值分解，可以得到一组向量{sj}(j＝1,2,…)，满足：

[aq]{sj}＝{0}(4)

则{sj}为齐次线性方程组式(3)的通解，称作力密度模态。

进一步，步骤9)中所述单方向力密度法的原理及实现过程为：

对模型b的每个节点施加沿z向的外荷载pi，则模型b第i个节点的平衡方程为：

其中(xi,yi,zi)为第i个节点的x、y、z坐标，n为连接到第i个节点的单元数量，lk、fk和(xk,yk,zk)(k＝1,2,…,n)分别为连接到第i个节点的第k个单元的长度、内力和另一端点的x、y、z坐标；引入力密度qk＝fk/lk，可将式(5)写为：

由式(1)-式(4)可知，当采用步骤8)得到的力密度时，式(6)的前两个方程自动成立，只需对第三个方程进行求解；

设模型b有b个单元，m个节点，其中待找形的节点和固定的外环支座节点的数量分别为mf和mc，引入b×m的拓扑矩阵：

在[c]中将待找形的节点排列在外环支座节点之前，可将[c]拆分为自由节点拓扑矩阵[cf]和约束节点拓扑矩阵[cc]，即c＝[[cf][cc]]；对模型b的所有节点列出z向平衡方程并组集，可写成：

[cf]^t[q][cf]{zf}+[cf]^t[q][cc]{zc}＝{p}(8)

其中{zf}为待求解的节点z坐标向量，{zc}为外环支座节点的z坐标向量，{p}为节点外荷载向量，[q]为力密度对角矩阵；求解式(8)，即得自由节点的z坐标：

{zf}＝([cf]^t[q][cf])^-1({p}-[cf]^t[q][cc]{zc})(9)

以上求解意味着在模型b的找形过程中只需更新节点的z坐标，而x、y坐标不会发生变化，因而撑杆或吊索能自动保持竖直；由于该方法实现了仅在z向进行找形，故称之为单方向力密度法。

进一步，步骤12)中考虑自重或其他荷载对找形结果进行修正的具体过程为：找形完成后，通过初步设计确定索桁结构各构件的规格和预应力，得到结构设计模型，称为模型d；提取模型d各撑杆或吊索的预应力；约束模型d所有通过找形获得的节点的z向自由度，在结构自重或其他荷载作用下进行静力计算，将各约束反力值叠加至相应的撑杆或吊索预应力，作为修正采用的外荷载；施加外荷载至模型b的相应节点；将模型b的力密度模态进行线性组合，当力密度模态唯一时，可直接乘以调整系数，所得结果作为修正采用的力密度；对模型b进行带荷载的单方向力密度法找形；根据找形结果修正模型d的找形节点坐标，若修正后的模型d几何尺寸不满足要求，则更新力密度模态组合系数或调整系数，重新进行修正，直至模型d的几何尺寸满足要求；重复上述过程，直至单次修正幅度小于预设限值；最后根据模型d找形部分的索长和相应力密度值，计算修正的找形部分预应力。

本发明具有以下有益技术效果：

1.可在给定屋面或幕墙几何、保持撑杆或吊索竖直的前提下进行索桁结构的找形，使找形结果完全符合预期的建筑造型；

2.适用范围广，可以用于不同形式的屋面或幕墙曲面、边界形状和车辐式、平行式、交叉式等多种索桁架布置方式；

3.提出力密度模态的概念和单方向力密度法，找形过程中仅更新节点的z坐标，节点x、y坐标自动满足平衡方程，无需进行更新，从而使撑杆或吊索自动保持竖直；

4.控制参数少，可以针对给定的屋面或幕墙几何形状快速给出一系列不同尺寸的找形结果及对应的内力分布，便于建筑方案比选和结构优化；

5.找形过程与修正过程相对独立，找形过程中无需进行静力计算，因此与构件截面尺寸和荷载无关，可以使找形更加快速、便捷；

6.找形完成后考虑自重或其他荷载进行修正，可使索桁结构初始态与零状态的几何构形基本一致。

附图说明

图1为本发明的找形方法流程图；

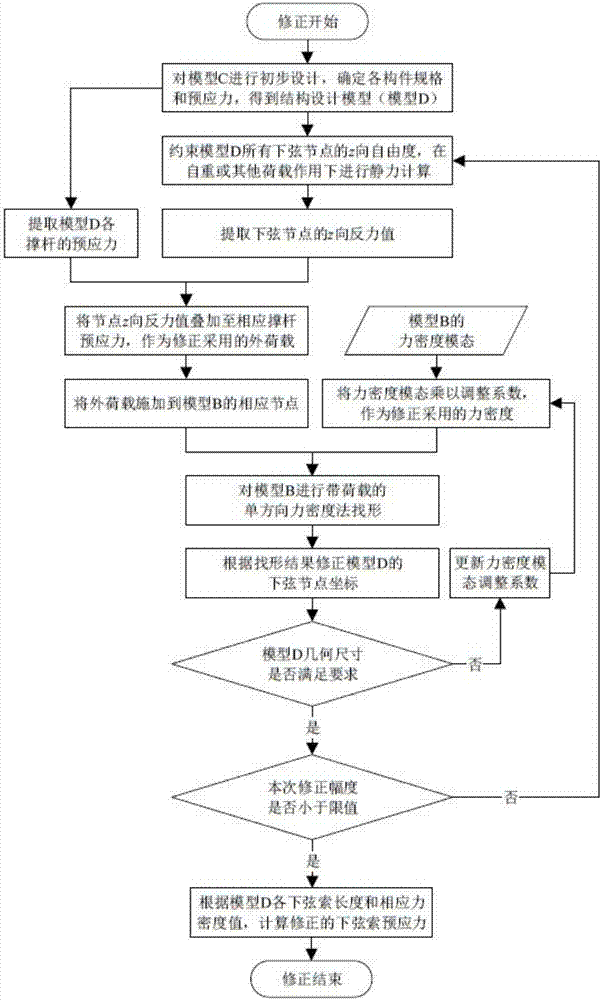
图2为本发明的修正方法流程图；

图3为几何给定的索桁结构上弦索几何模型与撑杆初始几何模型组成的找力模型，即模型a；

图4为基于索桁结构下弦索初始几何模型形成的找形模型，即模型b；

图5为找形完成的模型b；

图6为找形完成的索桁结构，即模型c；

图7为模型a局部结构示意图；

图8为模型b局部结构示意图；

图9为找形完成的模型b局部结构示意图；

图10为模型c局部结构示意图；

图11为内环水平投影和索桁架水平投影几何关系示意图；

其中：1为上弦节点，2为上弦索，3为下弦节点，即撑杆下端点，4为撑杆，5为外环支座节点，6为下弦索，7为模型b找形采用的外荷载；8为内环水平投影；9为索桁架水平投影。

具体实施方式

下面，参考附图，对本发明进行更全面的说明，附图中示出了本发明的示例性实施例。然而，本发明可以体现为多种不同形式，并不应理解为局限于这里叙述的示例性实施例。而是，提供这些实施例，从而使本发明全面和完整，并将本发明的范围完全地传达给本领域的普通技术人员。

如图1所示，本发明了提供了一种索桁结构找形方法，包括以下步骤：

步骤1：建立符合给定屋面几何形状的索桁结构上弦节点1，根据拓扑关系连接各节点，得到上弦索2的几何模型；

步骤2：将各上弦节点1沿竖直方向向下偏移任意距离，得到各下弦节点3的初始位置，连接相应的上、下弦节点得到撑杆4的初始几何模型；

步骤3：约束外环支座节点5及撑杆4的下端点3，得到图3和图7所示的找力模型，命名为模型a；

步骤4：另建图4和图8所示的找形模型b，根据步骤2中下弦节点3的初始位置建立下弦索6的初始几何模型，并约束外环支座节点5；

步骤5：组集模型a的平衡矩阵并进行奇异值分解，得到其唯一的自应力模态；

步骤6：提取模型a自应力模态中撑杆的对应数值，所得结果作为找形时的外荷载7；

步骤7：以力密度为变量建立模型b的x向和y向平衡方程组，组集方程组的系数矩阵，称为力密度平衡矩阵，对矩阵进行奇异值分解，得到模型b满足x向和y向平衡条件的唯一力密度模态；

步骤8：将模型b的力密度模态乘以调整系数，所得结果作为找形采用的力密度；

步骤9：采用步骤8得到的力密度，并将步骤6得到的外荷载7施加到模型b的相应节点3，对模型b进行带荷载的力密度法找形，得到图5和图9所示的满足平衡条件和撑杆4竖直要求的下弦节点3坐标，由于找形过程中各节点3的x、y坐标自动满足平衡，可仅更新z坐标，故称之为单方向力密度法；

步骤10：利用模型a中的上弦节点1坐标和找形后模型b中的下弦节点3坐标，建立图6和图10所示的索桁结构整体几何模型，命名为模型c；

步骤11：检查模型c的几何尺寸是否满足与建筑功能相关的要求，若满足则进入后续步骤，若不满足则返回步骤8，更新力密度模态调整系数，并重新进行找形，直至得到几何尺寸满足要求的的索桁结构；

步骤12：组集模型c的平衡矩阵并进行奇异值分解，得到找形完成的索桁结构自应力模态。

上述步骤未考虑结构自重或其他荷载的影响。找形完成后，通过初步设计确定索桁结构各构件的规格和预应力，得到结构设计模型，称为模型d。之后按图2所示步骤对找形结果进行修正，修正过程为：提取模型d各撑杆4的预应力；约束模型d所有下弦节点3的z向自由度，在结构自重或其他荷载作用下进行静力计算，将各约束反力值叠加至相应的撑杆4预应力，作为修正采用的外荷载；施加外荷载至模型b的相应节点3；将模型b的力密度模态乘以调整系数，所得结果作为修正采用的力密度；对模型b进行带荷载的单方向力密度法找形；根据找形结果修正模型d的下弦节点3坐标，若修正后的模型d几何尺寸不满足要求，则更新力密度模态调整系数，重新进行修正，直至模型d的几何尺寸满足要求；重复上述过程，直至单次修正幅度小于预设限值；最后根据模型d各下弦索6长度和相应力密度值，计算修正的下弦索6预应力。该修正过程仅对索桁结构下弦索6的形状和预应力进行微调，不会改变上弦索2的几何形状，且撑杆4仍旧保持竖直。修正后，索桁结构初始态与零状态的几何构形基本一致。

步骤7中所述力密度平衡矩阵和力密度模态具体含义及计算方法为：

为模型b的第i个下弦节点建立x向和y向平衡方程：

其中(xi,yi)为第i个节点3的x、y坐标，n为连接到第i个节点3的下弦索6的数量，lk、fk和(xk,yk)(k＝1,2,…,n)分别为连接到第i个节点3的第k根下弦索6的长度、内力和另一端点的x、y坐标。引入力密度qk＝fk/lk，可将式(1)变换为：

在式(2)中，(xi,yi)、(xk,yk)已经根据各节点3的水平位置给定，而qk未知，因此可以将式(2)视为关于qk的方程组。为模型b所有节点3建立同样的平衡方程，组集后写成矩阵形式：

[aq]{q}＝{0}(3)

式(3)中的矩阵[aq]称为模型b的力密度平衡矩阵，{q}为满足模型b各节点3水平平衡条件的力密度；

将[aq]进行奇异值分解，可以得到一组向量{sj}(j＝1,2,…)，满足：

[aq]{sj}＝{0}(4)

则{sj}为齐次线性方程组式(3)的通解，称作力密度模态。由齐次线性方程组通解的性质可知，向量{sj}的线性组合仍是式(3)的解，因此可以将力密度模态进行线性组合，得到满足x向和y向平衡条件的力密度。通过合理的结构布置，可使模型b拥有唯一的力密度模态，此时将力密度模态乘以调整系数即可得到力密度。

对于本实施例的车辐式索桁结构，将结构投影至水平面，则内环上的每个下弦节点3的投影均连接有两侧的内环投影8和一榀索桁架投影9，如图11所示。当每榀索桁架投影9均沿相应内环8投影夹角的角平分线方向布置时，模型b存在唯一的力密度模态，同时这也是步骤5中模型a存在唯一自应力模态的充分条件。

步骤9中所述单方向力密度法的原理及实现过程为：

对模型b的每个下弦节点3施加沿z向(即撑杆方向)的外荷载7(用pi表示)，则模型b第i个节点3的平衡方程为：

其中(xi,yi,zi)为第i个节点3的x、y、z坐标，n为连接到第i个节点3的下弦索6的数量，lk、fk和(xk,yk,zk)(k＝1,2,…,n)分别为连接到第i个节点3的第k根下弦索的长度、内力和另一端点的x、y、z坐标。引入力密度qk＝fk/lk，可将式(5)写为：

由式(1)-式(4)可知，当采用步骤8得到的力密度时，式(6)的前两个方程自动成立，只需对第三个方程(即z向平衡方程)进行求解。

设模型b有b根下弦索6，m个节点，其中待找形的下弦节点3和固定的外环支座节点5的数量分别为mf和mc，引入b×m的拓扑矩阵：

在[c]中将下弦节点3排列在外环支座节点5之前，可将[c]拆分为自由节点拓扑矩阵[cf]和约束节点拓扑矩阵[cc]，即[c]＝[[cf][cc]]；对模型b的所有节点3列出z向平衡方程并组集，可写成：

[cf]^t[q][cf]{zf}+[cf]^t[q][cc]{zc}＝{p}(8)

其中{zf}为待求解的节点3的z坐标向量，{zc}为外环支座节点5的z坐标向量，{p}为节点外荷载7向量，[q]为力密度对角矩阵；求解式(8)，即得自由节点的z坐标：

{zf}＝([cf]^t[q][cf])^-1({p}-[cf]^t[q][cc]{zc})(9)

以上求解意味着在模型b的找形过程中只需更新节点3的z坐标，而x、y坐标不会发生变化，因而撑杆能自动保持竖直；由于该方法实现了仅在z向进行找形，故称之为单方向力密度法。

上面所述只是为了说明本发明，应该理解为本发明并不局限于以上实施例，符合本发明思想的各种变通形式均在本发明的保护范围之内。