一种短时负荷预测方法及装置与流程

本发明涉及电力负荷预测技术领域，更具体地说，涉及一种短时负荷预测方法及装置。

背景技术：

负荷预测是电力市场发展的必要手段之一，能够准确的预测到某一具体时刻的电力负荷值，对电力系统具有重要的经济意义和社会意义。短时负荷预测是对某日内每个时刻(例如每日的负荷曲线由24、48、96、144或288个点组成)的负荷，其目的是安排日开停机组计划和发电计划。

近些年来，人工智能及机器学习在短时负荷预测研究领域得到迅猛发展，学者们通过数学建模对负荷预测进行了一系列研究，提出了许多解决负荷预测问题的方法，一般在进行上述数学建模时均需要使用到历史上产生的负荷数据，但是，如果这些负荷数据中存在异常的数据，就会对数学建模产生影响，进而导致对应预测模型的预测精度大大降低，对应的，利用这种预测模型实现负荷的预测时会出现精度较低的情况。

综上所述，如何提供一种预测精度较高的短时负荷预测的技术方案，是目前本领域技术人员亟待解决的问题。

技术实现要素：

本发明的目的是提供一种短时负荷预测方法及装置，以达到较高的预测精度。

为了实现上述目的，本发明提供如下技术方案：

一种短时负荷预测方法，包括：

获取包括环境数据及对应负荷数据的历史数据，并利用非参数概率密度函数估计建立所述环境数据及所述负荷数据之间的关系；

基于所述关系获取所述历史数据中的自适应遗忘因子，构建基于所述自适应遗忘因子的时变cook距离统计量；

利用所述时变cook距离统计量对所述历史数据中的负荷数据进行检测，如果检测出异常数据，则利用非参数概率密度函数估计基于所述异常数据对应的环境数据对所述异常数据进行修复；

对修复完成的所述异常数据及其他所述历史数据进行训练得到对应的负荷预测模型，并运用mcso算法对所述负荷预测模型进行优化，以利用该负荷预测模型实现短时负荷预测。

优选的，获取包括环境数据及对应负荷数据的历史数据，包括：

获取包括环境数据及对应负荷数据的历史数据，其中所述环境数据包括湿度数据及温度数据。

优选的，基于所述关系获取所述历史数据中的自适应遗忘因子，包括：

利用递归最小二乘法基于所述关系获取所述历史数据中的自适应遗忘因子。

优选的，对修复完成的所述异常数据及其他所述历史数据进行训练得到对应的负荷预测模型，包括：

利用orelm对修复完成的所述异常数据及其他所述历史数据进行训练得到对应的负荷预测模型。

一种短时负荷预测装置，包括：

处理模块，用于：获取包括环境数据及对应负荷数据的历史数据，并利用非参数概率密度函数估计建立所述环境数据及所述负荷数据之间的关系；

构建模块，用于：基于所述关系获取所述历史数据中的自适应遗忘因子，构建基于所述自适应遗忘因子的时变cook距离统计量；

修复模块，用于：利用所述时变cook距离统计量对所述历史数据中的负荷数据进行检测，如果检测出异常数据，则利用非参数概率密度函数估计基于所述异常数据对应的环境数据对所述异常数据进行修复；

训练模块，用于：对修复完成的所述异常数据及其他所述历史数据进行训练得到对应的负荷预测模型，并运用mcso算法对所述负荷预测模型进行优化，以利用该负荷预测模型实现短时负荷预测。

优选的，所述处理模块包括：

获取单元，用于：获取包括环境数据及对应负荷数据的历史数据，其中所述环境数据包括湿度数据及温度数据。

优选的，所述构建模块包括：

构建单元，用于：利用递归最小二乘法基于所述关系获取所述历史数据中的自适应遗忘因子。

优选的，所述训练模块包括：

训练单元，用于：利用orelm对修复完成的所述异常数据及其他所述历史数据进行训练得到对应的负荷预测模型。

本发明提供了一种短时负荷预测方法及装置，其中该方法包括：获取包括环境数据及对应负荷数据的历史数据，并利用非参数概率密度函数估计建立所述环境数据及所述负荷数据之间的关系；基于所述关系获取所述历史数据中的自适应遗忘因子，构建基于所述自适应遗忘因子的时变cook距离统计量；利用所述时变cook距离统计量对所述历史数据中的负荷数据进行检测，如果检测出异常数据，则利用非参数概率密度函数估计基于所述异常数据对应的环境数据对所述异常数据进行修复；对修复完成的所述异常数据及其他所述历史数据进行训练得到对应的负荷预测模型，并运用mcso算法对所述负荷预测模型进行优化，以利用该负荷预测模型实现短时负荷预测。本发明实施例提供的上述技术方案，在利用获取到的历史数据进行负荷预测模型的建立前，需要利用基于自适应遗忘因子的时变cook距离统计量检测负荷数据中是否存在异常数据，并利用非参数概率密度函数估计基于检测出的异常数据对应的环境数据对异常数据进行修复，以在修复完成后利用修复完成的异常数据及其他全部历史数据训练负荷预测模型，并运用mcso算法对负荷预测模型进行优化，利用该负荷预测模型实现短时负荷预测，从而避免异常数据对对应的负荷预测模型产生的影响，大大提高了负荷预测模型的预测精度，进一步提高了利用该负荷预测模型实现短时负荷预测的预测精度。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据提供的附图获得其他的附图。

图1为本发明实施例提供的一种短时负荷预测方法的流程图；

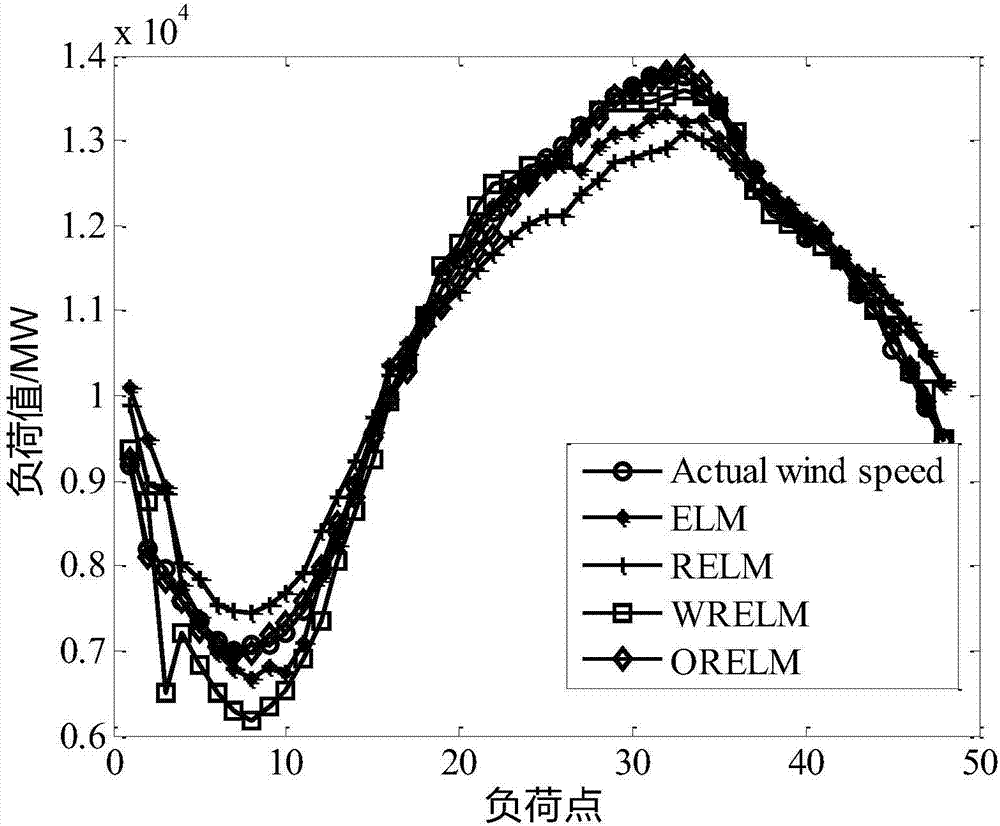
图2为本发明实施例提供的一种短时负荷预测方法中不同预测方法的第一种结果示意图；

图3为本发明实施例提供的一种短时负荷预测方法中不同预测方法的第二种结果示意图；

图4为本发明实施例提供的一种短时负荷预测方法中预测日温度和湿度的变化情况的示意图；

图5为本发明实施例提供的一种短时负荷预测方法中考虑累积效应前后的预测结果对比的示意图；

图6为本发明实施例提供的一种短时负荷预测装置的结构示意图。

具体实施方式

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

请参阅图1，其示出了本发明实施例提供的一种短时负荷预测方法的流程图，可以包括以下步骤：

s11：获取包括环境数据及对应负荷数据的历史数据，并利用非参数概率密度函数估计建立环境数据及负荷数据之间的关系。

需要说明的是历史数据即为历史上已经产生的数据，而对历史数据的数据采样频率可以为30分钟，历史数据包括环境数据及负荷数据，其中环境数据及负荷数据是对应的，也即在某一时刻的环境数据与该时刻的负荷数据相对应。利用非参数概率密度函数估计(non-parameterprobabilitydensityfunctionestimation,npdf)建立环境数据及负荷数据之间的关系，也即获取到环境数据及负荷数据之间的对应关系，通过建立的该关系，能够通过某一时刻的环境数据得知该时刻的负荷数据；通过该关系的建立能够实现对于环境数据对负荷数据的影响的详细分析，以保证后续步骤的顺利实现。具体来说，由于负荷具有季节性的特性，即负荷在不同季节随环境因素的变化情况是不同的，因此步骤s11在获取到历史数据后，还可以将历史数据基于该历史数据的产生时间划分到不同季节，进而建立不同季节中环境数据及负荷数据的关系，从而对于待检测的负荷点，可以利用其对应季节建立的关系来判断该负荷点是否为异常值，也即判断该负荷点的负荷数据是否为异常数据。

s12：基于关系获取历史数据中的自适应遗忘因子，构建基于自适应遗忘因子的时变cook距离统计量。

基于上述关系能够获取到历史数据中的自适应遗忘因子，进而基于该自适应遗忘因子构建对应的时变cook距离统计量(time-varyingcookdistance,tvcd)，其中引入自适应遗忘因子能够对实时的负荷数据进行自适应追踪，从而确定出负荷数据中异常的负荷数据(即异常数据)，进而供后续对该数据的修复。

s13：利用时变cook距离统计量对历史数据中的负荷数据进行检测，如果检测出异常数据，则利用非参数概率密度函数估计基于异常数据对应的环境数据对异常数据进行修复。

利用时变cook距离统计量对历史数据中的负荷数据进行检测，如果未检测出异常数据，则可以直接利用历史数据进行负荷预测模型的训练，否则，则需要对检测出的异常数据进行修复，本申请中利用非参数概率密度函数估计对异常数据进行修复，具体来说，可以利用非参数概率密度函数估计构建实时负荷数据与环境数据的随机模型，以利用该模型求得与异常数据对应环境数据具有对应关系的负荷数据作为异常数据的代替数据，从而实现异常数据的修复。简单来说，步骤s11至步骤s13通过充分考虑历史实时环境数据对负荷数据的影响，采用非参数概率密度函数估计，考虑到季节变动和随机波动的时间序列特性，对异常的负荷数据进行自适应修复。另外需要说明的是本申请中的异常数据可以是指出现异常或者是具有强影响的数据，主要可以包括两类数据：(1)用电信息采集系统采集错误的数据；(2)负荷局部离群数据，即噪声样本。

s14：对修复完成的异常数据及其他历史数据进行训练得到对应的负荷预测模型，并运用mcso算法对负荷预测模型进行优化，以利用该负荷预测模型实现短时负荷预测。

对包含有修复完的异常数据的历史数据进行训练得到对应的负荷预测模型，并运用mcso(modifiedcrisscrossoptimizationalgorithm，改进的纵横交叉)算法对负荷预测模型的模型参数进行优化，从而将需要预测时刻的环境数据作为该模型的输入，即可得到预测的该预测时刻的负荷数据，从而实现预测时刻负荷数据的预测。

本发明实施例提供的上述技术方案，在利用获取到的历史数据进行负荷预测模型的建立前，需要利用基于自适应遗忘因子的时变cook距离统计量检测负荷数据中是否存在异常数据，并利用非参数概率密度函数估计基于检测出的异常数据对应的环境数据对异常数据进行修复，以在修复完成后利用修复完成的异常数据及其他全部历史数据训练负荷预测模型，利用该负荷预测模型实现短时负荷预测，从而避免异常数据对对应的负荷预测模型产生的影响，大大提高了负荷预测模型的预测精度，进一步提高了利用该负荷预测模型实现短时负荷预测的预测精度。另外采用mcso算法对负荷预测模型的模型参数进行优化，能够进一步提高负荷预测模型的预测精度。

本发明实施例提供的一种短时负荷预测方法，获取包括环境数据及对应负荷数据的历史数据，可以包括：

获取包括环境数据及对应负荷数据的历史数据，其中环境数据包括湿度数据及温度数据。

本发明实施例提供的技术方案中，环境数据可以包括温度和湿度，当然还可以根据实际需要设定，均在本发明的保护范围之内。本申请中选用温度和湿度作为环境数据，能够实现所需数据的快速获取，并在本申请中同时考虑温度热累积效应和湿度热累积效应对电力负荷的影响，进一步提高了短时负荷预测的预测精度。

本发明实施例提供的一种短时负荷预测方法，基于关系获取历史数据中的自适应遗忘因子，可以包括：

利用递归最小二乘法基于关系获取历史数据中的自适应遗忘因子。

其中，利用递归最小二乘法基于关系获取历史数据中的自适应遗忘因子，也即在建立关系时即利用递归最小二乘法建立对应的递归最小二乘模型，进而由该模型中获取到自适应遗忘因子，从而实现利用递归最小二乘法对自适应遗忘因子的获取。具体来说，可以包括：

利用非参数概率密度函数估计建立不同季节温度、湿度与负荷数据的关系，引入实时负荷数据分别与温度和湿度的递归最小二乘(recursiveleastsquare，rls)模型：

其中，yt为实时负荷数据；为模型输入变量；βt为模型的参数；tt和ht分别表示温度变量和湿度变量；ηt为独立同分布的随机变量序列，并且e(ηt)＝σ²＜∞其中e(·)表示求期望，σ²表示方差；q表示预测时刻的前q个时刻的负荷值、温度和湿度作为模型的输入变量。

参数向量估计的迭代计算过程如下式(2)和(3)：

其中，为βt的参数估计；为增益矩阵预测值；为模型预测误差。

由式(2)和(3)可知，的递归值与λ有关，选择适当的λ对模型的自适应过程有着重要的影响，λ即为获取的自适应遗忘因子。

基于关系获取历史数据中的自适应遗忘因子，构建基于自适应遗忘因子的时变cook距离统计量并利用时变cook距离统计量对历史数据中的负荷数据进行检测，可以包括：

在上述递归过程中，给出基于自适应遗忘因子的时变cook距离统计量：

式中，和分别为未将自适应遗忘因子应用于递归过程中时和的值；m为向量的长度。t时刻λ＝1时，参数矩阵从到的变化受t时刻的负荷值的影响，也说明历史负荷具有很强的影响力；为σ²的一致估计，有

cook距离ct利用非线性测量来自适应设置自适应遗忘因子λt，通过最小阈值λmin来提高rls算法的鲁棒性。对于大样本数据，cook距离与卡方分布概率相结合估计λt，即

式中：p为卡方分布概率函数，λt为cook距离利用卡方分布计算得到的结果；为服从自由度m的卡方分布。

公式(5)将cook距离变换到区间[0,1]，通过设置自适应遗忘因子的阈值，在自适应递推过程中削弱异常数据(异常值或强影响值)的负面影响，进而确保自适应过程的稳定性。

基于cook距离的自适应遗忘因子表达式为：

λt＝λmin+(1-λmin)λt(6)

式中：λmin为自适应遗忘因子的最小值。

由式(4)得出基于自适应遗忘因子的时变cook距离统计量，通过cook距离和f分布概率进行估计，在给定的置信水平α下，如果t时刻的cook距离满足不等式(7)，即

ct＞f(α,p,n-p)(7)

则可以判定该时刻负荷为异常数据(异常值或强影响值)。

式中，f(α,p,n-p)为服从自由度为p和n-p的f分布；n为负荷采样样本个数；p为模型输入变量个数。在这种情况下，需要通过自动调节自适应遗忘因子λt来重新确定模型参数，并且对于异常数据需要通过npdf来修复。

利用非参数概率密度函数估计基于异常数据对应的环境数据对异常数据进行修复，可以包括：

根据检测出来的负荷异常数据(异常值或强影响值)，利用npdf对异常数据进行修复，保证数据的连续性和完整性。现在问题转化为给定温度和湿度的条件下，负荷的估计值。

给定温度、湿度的负荷条件概率模型：

ft(y|t)＝κtft(y,t)(10)

ft(y|h)＝κhft(y,h)(11)

其中，κt、κh为常数，由以下公式求得：

其中，y表示负荷值，ymax、ymin分别为负荷最大值和最小值，t和h分别为温度和湿度变量。

通过给定时间下的温度和湿度，求得负荷的期望值：

负荷的估计值：

其中，为每个季节参加建模总天数日负荷的平均值。本申请中，t时刻异常负荷的估计值为t时刻负荷和温度估计值、负荷和湿度估计值的平均值。

本发明实施例提供的一种短时负荷预测方法，对修复完成的异常数据及其他历史数据进行训练得到对应的负荷预测模型，可以包括：

利用orelm对修复完成的异常数据及其他历史数据进行训练得到对应的负荷预测模型。

具体来说，该步骤可以包括：

给定n个训练数据集其中xi＝[xi1,xi2,…,xir]^t为输入向量，r代表输入变量的个数，i表示隐含层节点个数，oi为相应的期望输出值。对于包含有个隐含层，激活函数为g(x)的极限学习机数学模型可以表示为：

其中wi＝[wi1,wi1,…,w1r^t]为连接第i个隐含层神经元和输入层的权值，为第i个隐含节点的偏差。βi＝[βi1,βi2,…,βir]^t为连接第i隐含层神经元和输出层的权值。

公式(20)可以用矩阵的形式简写：

hβ＝o(21)

其中，

式中，h为隐含层输出层矩阵。

输出权值的求解是保证损失函数取得最小值，引入调节系数γ来权衡训练误差和输出权值，利用1-范数的稀疏特性，在经典orelm损失函数的基础上进行改进，改进后的损失函数如下：

利用增广拉格朗日算子求解(24)中的最优解。构建拉格朗日方程：

式中，π为拉格朗日因子，μ为惩罚子，此次取μ＝2n/||o||1,||·||1表示1-范数，e为训练误差。

得到递归函数：

根据递归，可以得到(ek,βk)的关系如下：

βk+1＝(h^th+2/γμi)-¹h^t(o-ek+πk/μ)(27)

其中，u＝o-hβk+1+πk/μ为辅助参数。

引进训练误差e，利用误差反馈来自适应更新输出层权值β，形成具有异常鲁棒性的预测模型。1-范数的作用是利用其稀疏性的特点来减少异常值的干扰。

本发明实施例提供的一种短时负荷预测方法，运用mcso算法对负荷预测模型进行优化，可以包括：

假定父代粒子x(i)和x(j)在第d维进行横向交叉，计算公式如下：

其中,r1和r2为均匀分布于[0,1]的随机数，c1和c2为均匀分布于[-1,1]的随机数，mshc(i,d)和mshc(j,d)是x(i,d)和x(j,d)交叉产生的子代。

将执行完横向交叉后更新的种群作为纵向交叉的父代种群，假定粒子x(i)在第d1和d2维进行纵向交叉，计算公式如下：

其中，r为均匀分布于[0,1]的随机数；d为粒子的维度总数；m是种群数量。将横向交叉与纵向交叉产生的中庸解与父代粒子进行竞争，得到最优的种群。

通过种群适应度值中的变量τ²来自动调整pvc，其中τ²的表达式如下：

其中fi为粒子i的适应度值，favg为此时所有适应度的平均值，n为粒子个数；

最后，利用公式(32)可以得到纵向交叉概率pvc的线性表达式：

其中，pvcmax和pvcmin是纵向交叉概率pvc的最大值和最小值，表示t时刻的τ²值；以此得到负荷预测最优模型。

为考虑隐含层个数和调节系数γ取值对模型精度的影响，由于横向和纵向交叉均存在概率会影响到优化的结果。为了寻求最优化，大多数情况下会将横向交叉概率phc设置为1，但是纵向交叉概率pvc很难提前设定，因为pvc的值有时候会影响到mcso算法的全局搜索。

采用鲁棒极限学习机(extremelearningmachine,orelm)算法对负荷数据预测并采用mcso(modifiedcrisscrossoptimizationalgorithm)算法对模型参数进行优化；能够提高预测精度，而且对异常负荷具有自适应检测和修复能力。

另外需要说明的是，将本发明提供的上述技术方案可以具体应用如下：

采用某电力企业2006年1月-2010年12月的实时负荷数据、实时温度和实时湿度，将2006年-2009年的实时负荷数据对负荷预测模型进行训练，通过建立负荷预测模型来预测2010年的实时负荷值，将2010年的实际实时负荷值对负荷预测模型进行验证。

tvcd参数设置如下置信水平α＝0.0；5自适应遗忘因子最小值λmin＝0.6,0.7,；

msco参数设置如下：种群数量为20；最大迭代次数为500；phc＝1；pvcmax和pvcmin分别取为0.8和0.2；参数根据求出来的最优值分别取5和2的倍数。不同的预测方法最优参数如表1所示：

表1各种方法最优参数

由表1发现，本申请公开的技术方案(tvcd-npdf-orelm)中负荷预测模型最优参数隐含层神经网络个数最小，这样可以极大的提高预测时间。

用2010年的实时负荷来验证λmin＝0.6,0.7,0.8时对负荷预测精度的影响，并采用平均绝对百分比误差(meanabsolutepercentageerror,mape)评价指标来表征预测精度，即

式中：yi、ti为i时刻电力负荷的实际值和预测值；n为预测天数。

对比的结果如下表：

表2不同λmin的预测结果

由表2可知，λmin＝0.8时检测到异常(或强影响)负荷值的个数最多(27个)，通过npdf修复后的预测精度最高(mape值为1.13％)，体现了本申请公开的技术方案对于异常(或强影响)负荷值的修复能力。

为了验证本发明提出的tvcd-npdf-orelm负荷预测方法的精度，将其与elm算法、relm算法、wrelm算法的预测结果进行比较，并考虑异常负荷修复前后两种情况，结果如表3所示：

表3异常负荷修复前后各种方法预测精度比较

由表3知，每种方法在异常负荷修复前后预测精度都有明显的提高，尤其是本文提出的tvcd-npdf-orelm方法精度得到较大提高，这也验证了

前文介绍的orelm算法对负荷异常值具有抗干扰能力的特点。

为了验证本发明提出的tvcd-npdf-orelm负荷预测方法的精度，考虑极端天气因素的影响，并将其与elm算法、relm算法、wrelm算法的预测结果进行比较：

选取2010年夏天某一极端天气下的预测日(48个负荷点)进行分析。该预测日最高温度、日平均温度比往年同期分别高出9.7℃和8.3℃，相对湿度高出同期的23.2％，而且发现，比预测日前一天平均温度高出了10.5℃，属于典型的极端天气现象，四种方法预测结果如图2和图3所示。

显然，鲁棒tvcd-npdf-orelm预测方法预测误差波动比另外三种更小，对应的mape值为0.92％，说明气候因素的突然变化，鲁棒tvcd-npdf-orelm方法表现出很强的抗干扰能力，自适应修正模型参数来应对这种突发天气现象，从而提高预测精度。

对2010年夏季持续高温的某一周的负荷进行预测分析，该周天气呈现持续高温和潮湿状态，持续时间为3天(144个负荷点)，图4为预测日温度和湿度的变化情况，图5所示为考虑累积效应前后的预测结果对比。

由图4发现，选取的3个预测日的温度是先升高，达到最高温度31.9℃后慢慢下降，而且下降过程又有波动。未考虑气象因素累积效应时，由于温度的持续升高，导致在用电高峰期时的预测精度不高，随着温度的上升，负荷预测值比实际值偏低(图5)，mape值为2.96％。但是，考虑气象因素累积效应后，利用npdf对预测模型输入变量进行修正，使得预测精度明显提高，mape值为1.25％。

本发明实施例还提供了一种短时负荷预测装置，如图6所示，可以包括：

处理模块11，用于：获取包括环境数据及对应负荷数据的历史数据，并利用非参数概率密度函数估计建立环境数据及负荷数据之间的关系；

构建模块12，用于：基于关系获取历史数据中的自适应遗忘因子，构建基于自适应遗忘因子的时变cook距离统计量；

修复模块13，用于：利用时变cook距离统计量对历史数据中的负荷数据进行检测，如果检测出异常数据，则利用非参数概率密度函数估计基于异常数据对应的环境数据对异常数据进行修复；

训练模块14，用于：对修复完成的异常数据及其他历史数据进行训练得到对应的负荷预测模型，并运用mcso算法对负荷预测模型进行优化，以利用该负荷预测模型实现短时负荷预测。

本发明实施例提供的一种短时负荷预测装置，处理模块可以包括：

获取单元，用于：获取包括环境数据及对应负荷数据的历史数据，其中环境数据包括湿度数据及温度数据。

本发明实施例提供的一种短时负荷预测装置，构建模块可以包括：

构建单元，用于：利用递归最小二乘法基于关系获取历史数据中的自适应遗忘因子。

本发明实施例提供的一种短时负荷预测装置，训练模块可以包括：

训练单元，用于：利用orelm对修复完成的异常数据及其他历史数据进行训练得到对应的负荷预测模型。

本发明实施例提供的一种短时负荷预测装置中相关部分的说明请参见本发明实施例提供的一种短时负荷预测方法中对应部分的详细说明，在此不再赘述。

对所公开的实施例的上述说明，使本领域技术人员能够实现或使用本发明。对这些实施例的多种修改对本领域技术人员来说将是显而易见的，本文中所定义的一般原理可以在不脱离本发明的精神或范围的情况下，在其它实施例中实现。因此，本发明将不会被限制于本文所示的这些实施例，而是要负荷与本文所公开的原理和新颖特点相一致的最宽的范围。