一种不确定信息融合的应急物资分布需求预测方法与流程

本发明涉及一种应急物质需求预测技术，尤其涉及救援信息不确定性下应急事件的多源信息融合方式和信息规则挖掘方法，为准确的实施应急物质调度和救援提供依据。

背景技术：

在抗灾救援及处置突发事件的各项措施中，获取准确的救援信息特别是救援物资需求信息，是应急协同调度决策的先决条件。目前，应急救援物资需求预测主要从以下几个方面开展研究：⑴应急物资需求的专家经验预测法，主要利用历史震灾分析的数据和相关理论，根据统计的震级、死亡人数、受伤人数、倒塌房屋等多种参数，提出了需求预测模型。⑵应急救援物资需求的事例推理法，首先描述和提取发生或即将发生的灾害特征，根据这些特征从历史灾害库中搜索相似案例，对比分析新旧灾害案例，对历史灾害需求进行调整，从而获取本次灾害的需求。⑶基于空间遥感和gis技术的应急物资需求预测方法。一些学者对利用高清卫星遥感、航拍遥感影像结合gis来快速评估地震等巨灾后损失情况，评估结果可用于应急物资需求预测的重要依据。⑷基于时间序列的应急物资需求预测方法。该方法适用于动态需求预测，目前基于该类理论的自回归移动平滑法、指数平滑法和独立同分步法已经广泛用于应急需求预测。⑸基于神经网络的应急物资需求预测方法。由于应急物资需求影响的多元随机性，传统的数学建模难以精确预测，而神经网络因为其广泛的适应能力和学习能力，在非线性系统的预测方面得到广泛的应用；⑹不确定信息条件下实时应急需求预测方法，其目标是预测给定时期内每个受灾地区的动态应急需求。

但应急救援资源的需求预测，受到诸多社会、环境等因素影响，具有很强的时效性和阶段性，同时灾情和物资需求信息具有模糊性和不确定性，灾情发生短时间内获取的信息极为有限，需要结合对灾区历史统计数据挖掘基础上进行的资源需求分布预测，以保证预测的准确性。以往的模型缺乏将历史物资需求数据挖掘规则结合到不确定信息融合应急物资需求预测中去，因而难以获得准确的应急救援物资需求。

技术实现要素：

本发明的目的是提供一种不确定信息融合的应急物资分布需求预测方法，有效解决不确定性信息融合下的救援物资需求预测问题，可有效提高救援物资需求准确性，为航空救援调度和实施提供决策依据。

本发明公开的不确定信息融合的应急物资分布需求预测方法，包括如下步骤，

步骤1，分析历史灾情数据库中各范例的基本属性，提取范例的共同特征，将这些特征运用粗糙集方法进行简约；

步骤2，根据简约后的各条件属性对物资预测结果的影响程度计算出属性权重值；步骤3，对条件属性值和决策属性值相同的范例进行进一步简约；

步骤4，将进一步简约后的灾情数据运用k-means方法将案例分为k类，找出这些类的中心点，并根据当前案例与各类中心点之间的距离判断当前案例属于哪一类；

步骤5，根据范例相似度的计算方法，检索出相似度最高的历史目标范例；

步骤6，根据目标范例的物资消耗以及范例属性权重值来线性推测当前范例的物资需求量。

进一步的，步骤1包括：

步骤11，设s＝(c,b)为历史灾情范例数据库，cn为第n个范例，b为范例属性所组成的集合，即b＝f∪d，

其中，f＝{f1,f2,...,fm}为灾情范例的条件属性集，即和地震有关的情景特征因素信息集，fm为第m个灾情属性的信息；d＝{d1,d2,...,di}为决策属性集，即主要应急物资需求集，di为灾区第i类物资的需求量，d0表示耐用品需求量，d1表示消耗品需求量；

步骤12，给定各条件属性阈值，范例条件属性值满足阈值要求为1，否则为0，按此规则生成0-1信息表，如果c/ind(f)＝c/ind(f-{fm})，则属性fm是可以约简的，否则是不可约简的。

进一步的，步骤2包括：

步骤21，需计算出简约后范例的各条件属性对物资预测结果的影响程度，用属性权重值ωj表示。灾情范例条件属性集f＝{f1,f2,...,fm}的影响权重集为{ω1,ω2,...,ωm}，且满足：

步骤22，n(f)表示灾情范例在条件属性为f时的取值，当n(f)在范例库c＝{c1,c2,...,cn}中的取值差异比较大的时候，表明该条件属性对分类的判别影响也比较大，应赋予较高权重值；反之，当n(f)在分类中的取值差异比较小的时候，表明该条件属性对分类的判别影响也不大，应取较小的权重值；

步骤23，将灾情范例数据库中的每一个范例当做一类。范例ci在条件属性fj下的取值n(fj)为该案例在特征因素fj下的隶属度函数并有：

均方差为：

则可求得灾情范例各条件属性的权重ωj为：

进一步的，步骤3包括：f表示灾情范例条件属性的集合，d表示灾情范例决策属性的集合，则有：rij:des(fi)→des(dj)，fi∩dj≠φ表示由条件属性到决策属性的决策规则集；cover(rij)＝|fi∩dj|/|b|，fi∩dj≠φ为灾情救援优先级决策规则rij的覆盖度。

进一步的，步骤3还可以根据进一步简约后的范例构造救援优先级决策规则，统计各规则发生的频率并计算其覆盖度，当条件覆盖度大于一定阈值时，说明该规则成立，则可得出当前案例的救援优先级。

进一步的，救援优先级决策规则覆盖度等于各规则出现的频率之和，当覆盖度大于90％时，该规则成立。

进一步的，步骤4中是所采用的反馈补偿的k-means方法，即基于反馈补偿的k值确定算法。

进一步的，基于反馈补偿k-means的历史灾情范例聚类算法，其k值确定算法步骤为：

步骤41，设k＝2，计算k个聚类中心之间的欧式距离，再设k＝k+1，用同样的方法计算各聚类中心之间的平均间距；

步骤42，对比分类数目为k+1时各聚类中心的平均间距相较于分类数目为k时的平均间隔是否增大，增大则再令k＝k+1，重复以上步骤，否则确定k值。

进一步的，步骤5中是所采用相关系数法来进行相似度计算，相关系数法来进行相似度计算的步骤包括：

对灾情范例间的相似度采用如下相关系数进行计算，

相关系数的取值范围是[-1,1]，计算出的相关系数绝对值越大，表明灾情范例cx与灾情范例cy之间的相关度越高。

进一步的，步骤6中，假设相似度最大的历史目标灾情范例的属性分别为p1、p2、p3和p4，耐用品和消耗品的供应量分别为n1、n2，条件属性f1，f2，f3，f4的权重值分别为ω(f1)，ω(f2)，ω(f3)，ω(f4)当前灾情范例的对应属性分别为p1′、p2′、p3′和p4′，则当前灾情范例耐用品和消耗品的需求量n1′和n2′分别为：

n1′＝(p1/p1′×ω(f1)+p2/p2′×ω(f2)+p3/p3′×ω(f3)+p4/p4′×ω(f4))×n1

n2′＝(p1/p1′×ω(f1)+p2/p2′×ω(f2)+p3/p3′×ω(f3)+p4/p4′×ω(f4))×n2。

本发明具有如下有益效果如下：

1)利用粗糙集属性简约方法，属性的维数大大降低，有效减少灾害范例的冗余属性，提高运行效率，同时也在不失真的情况下节省了大量灾情数据的存储空间。

2)根据简约后的各条件属性对物资预测结果的影响程度计算出属性权重值的方法不仅克服了仅由专家主观性判断带来的误差，也提高了应急救援物资需求预测的精度。

3)本发明基于反馈补偿的k-means聚类算法和范例推理理论引入灾后应急救援物资需求预测这一领域，解决了不确定性救援信息融合条件下的预测准确性，提高了预测的准确性，为救援决策实施提供依据。

4)采用相关系数法来进行相似度计算较夹角余弦、杰卡德相似系数度量法等，相对误差更低，判断更加精准。

5)该发明可直接应用于航空应急救援指挥系统中，有效提高航空救援的效率。

6)根据本发明得到受灾点的救援优先级以及受灾点的物资需求量的预测结果，在救援调度过程中，根据救援优先级是确定救援的先后顺序，然后根据该地物资物资需求，并结合物资分配标准，进行调度。

附图说明

图1为本发明的应急物资需求预测流程图。

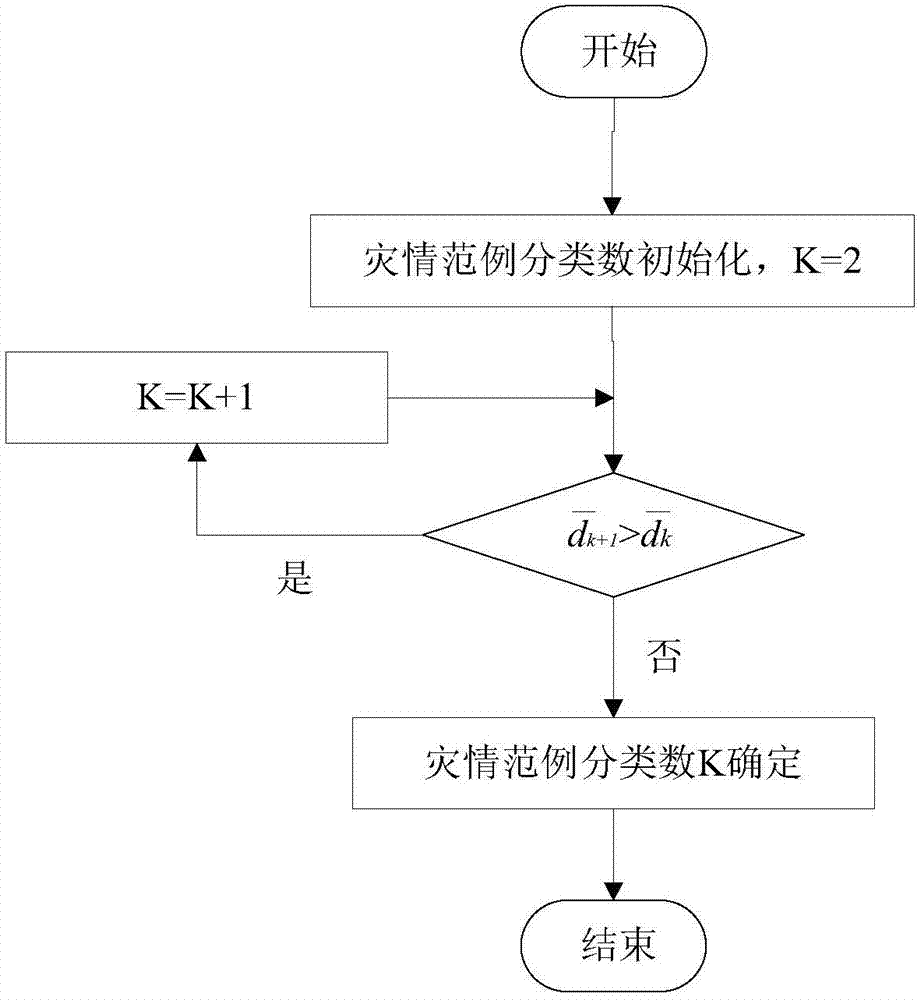
图2为基于反馈补偿的k值确定流程图。

图3为k＝2时的范例聚类结果。

图4为k＝3时的范例聚类结果。

图5为k＝4时的范例聚类结果。

图6为k＝5时的范例聚类结果。

具体实施方式

本发明运用基于反馈补偿k-means范例推理法预测灾区应急物资需求量的基本流程如图1所示，具体内容包括以下六个部分：

一、基于粗糙集的历史灾情范例属性简约

设s＝(c,b)为历史灾情范例数据库，cn为第n个范例，b为范例属性所组成的集合，即b＝f∪d。其中，f＝{f1,f2,...,fm}为灾情范例的条件属性集，即和地震有关的情景特征因素(如总人口、总面积、震级、震源深度、最高烈度、受灾人数、伤亡人数、砖混比例等)信息集，fm为第m个灾情属性的信息；d＝{d1,d2,...,di}为决策属性集，即主要应急物资需求集，di为灾区第i类物资的需求量。ωi为第i个范例的救援优先级。

给定各条件属性的阈值，若范例条件属性值满足阈值要求为1，否则为0，按此规则生成0-1信息表。

如果c/ind(f)＝c/ind(f-{fm})，即条件属性集f和条件属性集f-{fm}对任意范例c的决策属性无任何影响，二者造成的决策结果是一致的，则属性fm是可以约简的，否则是不可约简的。灾情范例简约是粗糙集理论的核心内容之一，它能在持续原有分类能力的情况下，去除冗余的数据和属性。

选取2008～2012年间的22个历史灾情数据作为训练样本(见表1)，样本的条件属性为：总人口(人)f1，总面积(平方公里)f2，震级(级)f3，震源深度(级)f4，最高烈度(级)f5，受灾人数(人)f6，伤亡人数(人)f7，砖混比例f8；决策属性为：耐用品需求量d0，消耗品需求量d1。将样本的各条件属性按表2的规则进行离散化处理，超过阈值的属性值设为1，否则设为0，离散化处理后的结果如表3所示。

表12008～2012年地震灾情历史范例数据

表2离散化处理规则

例如，获得的一条范例信息为：{总人口30000人，总面积332.9平方公里，震级6.2，震源深度12，最高烈度8，受灾人数2857，伤亡人数1489，砖混比例0.968}，参照表2将此条范例进行离散化处理，得到的结果为{0，0，1，1，1，0，0，1}，如表3中第一行范例数据所示。

表30-1离散化后的范例信息

从表3中可以看出，属性f1、f2对各范例的属性值相同，故只保留其中一个即可，在此保留属性f1；相同的，属性f3、f4、f5对各范例影响的属性值相同，保留属性f3；属性f6、f7对各范例的属性值相同，保留属性f7。属性简约后的范例信息如表4所示：

表4简约后的范例信息

属性简约后得到新的条件属性集为f＝{f1,f3,f7,f8}。利用粗糙集属性简约方法，属性的维数从8维降到了4维，能够有效减少灾害范例的冗余属性，提高运行效率，同时也在不失真的情况下节省了大量灾情数据的存储空间。

二、灾情范例属性权重值的计算

在不同的决策环境下，灾情范例的各条件属性对决策结果会有不同程度的影响，在此，需计算出简约后范例的各条件属性对物资预测结果的影响程度，用属性权重值ωj表示。

令灾情范例条件属性集f＝{f1,f2,...,fm}的影响权重集为{ω1,ω2,...,ωm}，且满足：

令n(f)表示灾情范例在条件属性为f时的取值，即，隶属度函数值。当n(f)在范例库c＝{c1,c2,...,cn}中的取值差异比较大的时候，表明该条件属性对分类的判别影响也比较大，应赋予较高权重值；反之，当n(f)在分类中的取值差异比较小的时候，表明该条件属性对分类的判别影响也不大，应取较小的权重值。因此，可将灾情范例数据库中的每一个范例当做一类。范例ci在条件属性fj下的取值n(fj)为该案例在特征因素fj下的隶属度函数nci(fj)，并有：

均方差为：

则可求得灾情范例各条件属性的权重ωj为：

将第一部分算例简约后的属性按照上述给出的权重值计算步骤求出条件属性f1、f3、f7、f8的权值分别为ω1＝0.13、ω3＝0.36、ω7＝0.31、ω8＝0.20，权重值越大，说明该条件属性对分类判别的作用越大，反之，权重值越小，说明该条件属性对分类判别的作用越小。在本发明的算例中，对分类判别影响最大的因素是震级，总人口数对分类判别的影响最小。这种权值计算方法不仅克服了仅由专家主观性判断带来的误差，也提高了应急救援物资需求预测的精度。

三、救援优先级决策规则覆盖度的计算

按照第一部分中灾情范例数据库的定义，则有：rij:des(fi)→des(dj)，fi∩dj≠φ表示由条件属性到决策属性的决策规则集。定义：cover(rij)＝|fi∩dj|/|b|，fi∩dj≠φ为灾情救援优先级决策规则rij的覆盖度，即在灾情范例数据库中，满足决策规则集rij的对象数占整个数据库对象数的比例。

对表4训练样本中条件属性值和决策属性值相同的范例进行简约所得决策规则如表5所示，运用本项目组开发的低空应急救援系统中的500条历史灾情数据构建范例数据库，统计决策规则发生的频率如下：

表5救援优先级决策规则

救援优先级决策规则覆盖度等于各规则出现的频率之和，当覆盖度大于90％时，则该规则成立。通过表5中各规则出现的频率，计算出满足该决策的样本数占整体样本数的92.3％，即规则覆盖率为92.3％，说明该规则成立，可用于实际救援。

由表5可知，救援优先级的判断规则可由总人口、震级、伤亡人数、砖混比例这四个属性决定，例如，当范例总人口数小于10万、震级是大于等于6、伤亡人数小于3000、房屋砖混比例大于等于0.6时，根据表5类比范例c1可推断出该范例的救援优先级是2；当总人口数大于等于10万、震级是大于等于6、伤亡人数大于等于3000、房屋砖混比例大于等于0.6时，类比范例c14可推断出当前范例的救援优先级是5，通过此决策规则可对各灾区的救援的优先级进行判定。四、基于反馈补偿k-means的历史灾情范例聚类算法

聚类分析方法作为一种被广泛使用的数据挖掘算法，能以较高的效率处理大数据，获得这些数据的分布特征及分布规则，并逐步应用于各领域。基于不同思想的聚类算法被提出，主要有基于划分的算法、基于层次的算法、基于密度的算法、基于网格的算法和基于模型的算法等，例如，k-means聚类算法、层次聚类算法、som聚类算法以及fcm聚类算法等。这些算法都能取得不错的聚类效果，其中应用最多且算法思想较为简单的是基于划分的k-means算法。

针对历史灾情数据多而杂的特点，本发明运用计算时间短、速度快、聚类效果较好的反馈补偿k-means算法对范例进行聚类分析，获得数据的分类，为第四部分找出与当前范灾情例相似度最高的历史灾情范例提供数据支持，并能提高对历史范例数据库检索的效率。

k-means算法采用欧式距离作为两个灾情范例相似度的评价指标，其基本思想是：随机选取历史灾情范例数据库中的k个范例作为初始聚类的中心，根据范例数据库中各灾情范例到k个中心的距离将其归类到距离最小的类中，然后计算各个类中灾情范例距离的平均值，更新每个类的中心，直到聚类中心不再发生变化。它的目标是将历史灾情范例数据库中的范例分成若干个类，使得同一类内的灾情范例之间的相似度尽可能大，不同类的灾情范例之间的相似度尽可能小。但，随着k-means算法研究的深入，一些不足也逐渐暴露出来，主要包括：k值难以预先确定以及初始的聚类中心选择困难等。k值的确定以及初始聚类中心的选择始终是k-means算法的重点及难点。

本发明提出的基于反馈补偿k-means的历史灾情范例聚类算法，其k值确定算法步骤为：首先，设k＝2，计算k个聚类中心之间的欧式距离，再设k＝k+1，用同样的方法计算各聚类中心之间的平均间距，对比分类数目为k+1时各聚类中心的平均间距相较于分类数目为k时的平均间隔是否增大，增大则再令k＝k+1，重复以上步骤，否则确定k值。此方法将灾情范例类间平均距离、类间重叠情况及类内数据的分散程度作为类内数目选择的重要参考，即k值的确定。假设为k个灾情范例聚类中心之间的平均距离，反馈补偿k值确定过程如图2所示。

在反馈补偿k-means灾情范例聚类算法中初始聚类中心点的选择规则为：第一个初始聚类中心点从历史灾情范例数据库中随机生成，第二个初始聚类中心点离第一个初始点最远，第三个初始聚类中心点离第一、第二个初始点的平均距离最远，反复如此，选出k个初始聚类中心。

对范例数据库中简约后的灾情数据运用k-means算法进行分类时，应先确定分类数，即k值。首先，设k＝2，计算出2个聚类中心之间的间距(即欧式距离)为217138.9999；再设k＝3，用同样的方法计算出3个聚类中心之间的平均间距为308223.8637，对比可知，k＝3时聚类中心的平均间距相较于k＝2的平均间隔明显增大，说明k＝3时的聚类效果要比k＝2时的聚类效果好；再设k＝4，计算出4个聚类中心之间的平均间距为320208.71559442，对比可知，k＝4时聚类中心的平均间距相较于k＝3的平均间隔明显增大，说明k＝4时的聚类效果要比k＝3时的聚类效果更好；再设k＝5，计算出5个聚类中心之间的平均间距为274362.7997，对比可知，k＝5时聚类中心的平均间距相较于k＝4的平均间隔明显减小，说明k＝5时的聚类效果要比k＝4时的聚类效果更差，分类不明显，故确定k值为4。如图3、4、5、6分别是k＝2、k＝3、k＝4、k＝5时的范例聚类结果。将类间平均距离、类间重叠情况及类内数据的分散程度作为类内数目选择的重要参考，通过对比以上实验聚类结果，可明显看出k＝2时范例聚类效果太分散，k＝3及k＝5时的范例聚类结果中各分类重叠区域较大，当k＝4时范例聚类效果较好，分类清晰可见。故选取k＝4作为分类数。

五、灾情范例相似度的计算

范例相似度计算的常用方法一般包括夹角余弦计算法、杰卡德相似系数法以及相关系数法等，其中夹角余弦更多的是从方向上区分差异，而对绝对的数值不敏感；杰卡德相似系数处理的都是非对称二元变量，并没有考虑向量中潜在数值的大小，而是简单的处理为0和1；相关系数法是度量随机向量之间的相关程度的一种方法，本发明采用相关系数对灾情范例间的相似度进行计算，定义如下：

相关系数的取值范围是[-1,1]，计算出的相关系数绝对值越大，表明灾情范例cx与灾情范例cy之间的相关度越高。

运用反馈补偿k-means方法对灾情数据分类后，计算当前灾情范例与各分类中心点的距离，判断当前案例属于哪一类，然后再将当前灾情范例与该类中每个算例进行相似度计算，找出相似度最大历史灾情范例。

从历史灾情范例中选出x＝(129320,6.3,4967,0.833)作为验算该算法的当前范例，当k＝4时，各分类中心点数据如表6所示：

表1当前范例与各中心点距离表

从表6可知，当前灾情范例x与上述四个中心点的欧式距离分别为：155114.910787806，104617.455838721，31896.3656220504，376667.762803906，与第二类中心点o2的距离最近，故将当前范例视为第二类。

运用matlab将属于第二类的数据筛选出来，并将当前范例x＝(129320,6.3,4967,0.833)与第二类中的每个范例进行相似度计算。计算结果中最大的相关系数为0.999983050183659，其对应的历史案例是c141＝(136455,8.4,4418,0.783)，故可参照该范例的历史需求数据对当前范例的物资需求量进行预测。

六、当前灾情范例物资需求预测

假设相似度最大的历史目标灾情范例的属性分别为p1、p2、p3和p4，耐用品和消耗品的供应量分别为n1、n2，条件属性f1，f2，f3，f4的权重值分别为ω(f1)，ω(f2)，ω(f3)，ω(f4)当前灾情范例的对应属性分别为p1′、p2′、p3′和p4′，则当前灾情范例耐用品和消耗品的需求量n1′和n2′分别为：

n1′＝(p1/p1′×ω(f1)+p2/p2′×ω(f2)+p3/p3′×ω(f3)+p4/p4′×ω(f4))×n1

n2′＝(p1/p1′×ω(f1)+p2/p2′×ω(f2)+p3/p3′×ω(f3)+p4/p4′×ω(f4))×n2

通过查找范例数据库可知，历史范例c141＝(136455,8.4,4418,0.783)对耐用品和消耗品的物资需求量分别为1100kg和700kg，利用线性相关算法对当前灾情范例的耐用品和消耗品的物资需求量进行预测，结果分别为：1049kg和668kg。即当前案例x＝(129320,6.3,4967,0.833)对耐用品的需求量为1049kg，对消耗品的需求量为668kg。

综合实施例的步骤，可得到两个结果数据，一个是受灾点的救援优先级，另一个是受灾点的物资需求量，在救援调度过程中，救援优先级是物资分配的参考标准，通常，对救援优先级高的受灾点予以优先救援，并且会先满足该点的物资需求，然后再逐个考虑下一救援优先级受灾点的物资需求的分配。

以上所述仅是本发明的优选实施方式，应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下还可以作出若干改进，这些改进也应视为本发明的保护范围。