基于MRVM‑AFOSM的边坡可靠度分析方法与流程
本发明属于边坡可靠度分析方法,具体涉及一种基于mrvm-afosm的边坡可靠度分析方法。
背景技术:
边坡工程包含有大量的不确定因素,采用常规的确定性方法难以准确评估其安全性态。而可靠度运用概率论和数理统计等方法,将各种不确定因素作为随机变量,分析边坡失稳的可能性,能够更合理地反映边坡的实际安全状况。
传统的边坡可靠度分析方法主要有:一阶可靠度方法(form)、二阶可靠度方法(sorm)、响应面法(rsm)、蒙特卡罗模拟(mcs)等,其中form又分为均值一次二阶矩(mvfosm)与改进一次二阶(afosm)。
mvfosm虽计算简便,但不考虑变量的概率分布,精度较低;aform精度较高,但需要大量计算,且要求边坡的功能函数为显式,常常难以满足;在form的可靠度计算结果的基础上,sorm对失效概率的计算方法进行改进,使失效概率结果更加准确;rsm尝试采用多项式函数代替未知的功能函数,但其计算量大,且不适于强非线性问题;随着计算机性能的提高,原理简单的mcs被提出,但对于失稳概率很小的问题,mcs计算效率、精度均较低。
随着智能算法的发展,将新型算法与传统可靠度相结合、交叉、融合的方法,避免了传统的功能函数计算,取得了良好的效果。大量学者将人工神经网络(ann)应用于可靠度计算,但ann存在所需训练样本大、计算结果不稳定、存在局部极小和“过拟合”等问题,且仍不能将功能函数显式表达。
一些学者尝试对支持向量机(svm)进行扩展、优化,并对其应用进行了探索。tan采用智能算法与mcs相结合计算边坡失稳概率,将svm与径向基函数神经网络(rbfn)进行了对比(tanxiaohui,biweihua,houxiaoliang,etal.reliabilityanalysisusingradialbasisfunctionnetworksandsupportvectormachines[j].computersandgeotechnics,2011,38:178-186)。何婷婷通过训练svm,将其作为响应面,并采用form、sorm、mcs进行可靠度计算,得到了良好的应用效果(何婷婷,尚岳全,吕庆,等.边坡可靠度分析的支持向量机法[j].岩土力学,2013,34(11):3269–3276)。fei采用高斯过程回归(gpr)与拉丁超立方抽样(lhs),将边坡稳定作为系统可靠度问题进行研究(kangf.hans.x.salgador.lij.j.systemprobabilisticstabilityanalysisofsoilslopesusinggaussianprocessregressionwithlatinhypercubesampling.computersandgeotechnics.2015.63,13–25)。此外,赵洪波利用svm将极限状态函数显式表达,并求解其偏导数(赵洪波.基于支持向量机的边坡可靠度分析[j].岩土工程学报,2007,29(6):819–823),随后结合mvfosm分析了边坡可靠度,为边坡可靠度提供了新的思路(zhaohongbo.slopereliabilityanalysisusingasupportvectormachine[j].computersandgeotechnics,2008,35:459-467)。随后,samui对相关向量机(rvm)代替极限状态函数进行了探索,但同样与mvfosm结合对边坡可靠度进行计算(pijushsamui,timlansivaara,dookiekim.utilizationrelevancevectormachineforslopereliabilityanalysis[j].appliedsoftcomputing,2011,11:4036-4040)。
相较于svm,rvm具有模型结构稀疏性、计算的复杂度相对较低、可提供方差、所需参数少和核函数不需要满足mercer条件等优势,但是,rvm虽然能够精确的对安全系数进行估算,但由于mvfosm自身缺点,导致rvm-mvfosm可靠度计算误差明显。
技术实现要素:
为了解决现有技术中存在的rvm-mvfosm可靠度计算误差明显的技术问题,本发明提供了以下技术方案:
基于mrvm-afosm的边坡可靠度分析方法,包括以下步骤:
步骤一、明确各影响因子的分布形式,构建样本的输入因子,然后计算所述样本安全系数,将该样本安全系数作为所述样本的输出因子;所述样本分为训练样本和测试样本;
步骤二、构建混合核函数mrvm,采用hs算法优化核参数值,使用所述训练样本对mrvm进行训练;
步骤三、使用经过训练的mrvm对所述测试样本的安全系数进行估算,并与所述步骤一中计算的测试样本安全系数比较,计算mae;当mae满足误差要求时,核参数值确定,mrvm训练完成,当mae不满足误差要求时,重复步骤二;
步骤四、采用afosm计算可靠度,初始设计验算点采用各影响因子的均值,使用mrvm计算所述设计验算点的边坡稳定性安全系数及一阶导数,得出新设计验算点;
步骤五、如果新设计验算点满足迭代终止条件,则终止迭代,得出边坡可靠度,如果新设计验算点不满足迭代终止条件,则重复步骤四。
作为本发明的进一步说明,所述步骤一中样本安全系数的计算方法为极限平衡法、塑性极限分析法或有限元法。
作为本发明的进一步说明,所述步骤二中混合核函数mrvm如下式所示,
k(x,xi)=mexp(-||x-xi||2/c2)+(1-m)[η(xxi)+r]q
式中,c为高斯核参数;η,r,q为多项式核参数;m为混合核函数的比例参数。
作为本发明的进一步说明,所述步骤二中hs算法包括以下步骤:
(1)初始化参数,主要参数包括:变量个数n、最大迭代次数tmax、和声记忆库的大小hms、记忆库取值概率hmcr、音调微调概率par、音调调节带宽bw,初始化和声记忆库,随机生成hms个和声z1,z2,…,zhms存放至和声记忆库,和声记忆库的和声数量始终保持一定,用于存储适应度f(z1)最优的hms个和声,和声记忆库hm的形式如下:
(2)构建新音调z′i,首先生成一个随机数rand1;若rand1<hmcr,新音调z′i在和声记忆库hm随机取值,后进入步骤(3);若rand1>hmcr,新音调z′i在取值范围内随机取值,后进入步骤(4);
(3)当新音调z′i来自和声记忆库时,则还有par的概率可对该音调进行微调,另有(1-par)的概率保持原值,完成所述微调后,新音调z′i生成,进入步骤(4);
(4)每一个新和声z′中的均由n个新音调z′i(i=1,2,…,n)组成,判断新音调是否全部生成,若没有全部生成,则需重复步骤(2)、(3),直至全部音调生成;
(5)更新和声记忆库,计算新和声的适应度,当其值优于和声记忆库中的适应度最差的和声时,用新和声代替最差和声,完成和声记忆库的更新;
(6)检查是否达到最大迭代次数,并重复步骤(2)~(5),直到迭代次数达到tmax时,计算停止。
作为本发明的进一步说明,所述步骤四中afosm计算可靠度的方法包括以下步骤:
使用训练完成后的mrvm对边坡安全系数进行计算,因此,极限状态函数值z可以表示为;
式中s为mrvm训练完成后支持向量的个数,即权重wi不为0的训练样本数;
mrvm的一阶导数为:
将mrvm的一阶导数代入afosm算法中,即可完成可靠度求解。
作为本发明的进一步说明,所述步骤五中迭代终止条件为:对于相邻两次计算所得的设计验算点,若两次设计验算点的相应自变量差值均小于误差允许值,则迭代停止。
与现有技术相比,本发明取得的有益效果为:
1、本发明将mrvm与afosm相结合,采用mrvm-afosm对边坡稳定进行可靠性分析。相较于rvm,混合核相关向量机(mrvm)兼具泛化能力、插值能力,具有更佳的拟合与预测能力,模型充分发挥了mrvm在处理非线性、小样本、高维数方面,计算速度快、准确率高等优势;模型采用hs优化后的mrvm对边坡安全系数进行估算,避免了传统极限状态函数不能显式表达、难以求解导数的问题;模型采用afosm代替mvfosm计算边坡可靠度,其设计验算点位于极限状态面上,可靠度计算结果更加准确。
2、在训练过程中,由于mrvm核参数较多,引入hs算法对核参数进行优化,可快速、准确的挑选出适宜的参数组合,大幅度提供mrvm的拟合、预测能力。
以下将结合附图及实施例对本发明做进一步详细说明。
附图说明
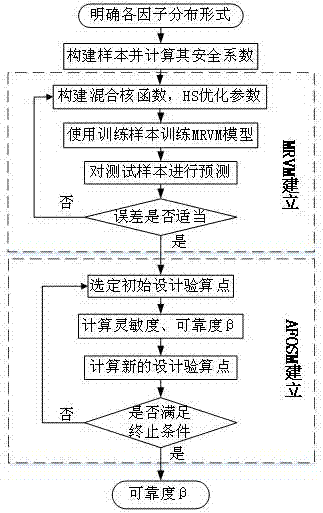
图1是本发明的分析方法计算流程图。
图2是本发明的分析方法中hs算法流程图。
图3是本发明实施例1中单层边坡形态图。
图4是本发明实施例1中单层边坡mrvm训练样本拟合效果图。
图5是本发明实施例1中单层边坡mrvm测试样本预测效果图。
图6是本发明实施例1中单层边坡可靠度计算结果示意图。
图7是本发明实施例2中多层边坡形态图。
图8是本发明实施例2中多层边坡mrvm训练样本拟合效果图。
图9是本发明实施例2中多层边坡mrvm测试样本预测效果图。
具体实施方式
为进一步阐述本发明达成预定目的所采取的技术手段及功效,以下结合附图及实施例对本发明的具体实施方式、结构特征及其功效,详细说明如下。
本发明提出将mrvm与afosm相结合,对边坡可靠度进行计算:首先采用hs算法对mrvm的混合核函数参数组合进行寻优,后采用mrvm对边坡极限状态函数进行拟合,实现边坡安全系数的快速、准确估算;同时,mrvm将功能函数显式化,便于求解极限状态函数的一阶导数;随后采用afosm计算设计验算点,得到更加精确的可靠度结果。
实施例1:
如图1所示,基于mrvm-afosm的边坡可靠度分析方法计算流程图,其具体包括以下步骤:
步骤一、明确各影响因子xi(i=1,2,…,k)的分布形式,构建样本的输入因子,该影响因子为影响边坡稳定的因子,然后采用传统的边坡稳定安全系数方法计算样本安全系数(本实施例采用极限平衡法中的bishop法计算边坡稳定安全系数),将该样本安全系数作为样本的输出因子;样本分为训练样本和测试样本;
步骤二、构建混合核函数mrvm,采用hs算法优化核参数值,使用训练样本对mrvm进行训练;
mrvm是对rvm的核函数进行了改进和扩展,其主体计算原理、步骤与rvm相同。
rvm是基于贝叶斯框架的概率学习模型。rvm通过定义受超参数控制的gaussian先验概率,在贝叶斯框架下进行机器学习,并利用主动相关判定理论(ard)移除不相关的点,从而得到稀疏化模型。rvm不仅可以定量预测,而且能够提供方差。
给定训练样本
式中,εn为误差,服从均值为0、方差为σ2的高斯分布;ωn为权重;ω0为基础量;k(x,xn)为核函数。设tn为独立分布,则似然函数可表示为:
式中,t为目标向量,t=(t1,t2,···,tn)t;w为参数向量,w=(ω0,ω1,···ωn)t;φ为基函数矩阵φ=[φ(x1),φ(x2),···φ(xn)],其中φ(xn)=[1,k(xn,x1),k(xn,x2),···,k(xn,xn)]t。
在利用最大化似然函数估计参数w的过程中,因参数过多可能导致过学习,因此假设参数ωi服从均值为0、方差为
式中,α为决定权值w先验分布的超参数,只与其对应权值w相关。
假定α、σ2均服从gamma先验概率,根据定义的似然分布和先验分布,可得w的后验分布:
式中,σ=(σ-2φtφ+a)-1,为后验协方差矩阵;a=diag(α0,α1,···,αn);μ=σ-2σφtt,为后验均值;m为相关向量机的个数。
通过对训练样本的似然函数式中的w进行积分,可得到由超参数α、σ2控制的边缘分布:
式中,ω=σ2e+φa-1φt,其中e为单位向量。
采用迭代的方法对上式进行求偏导,得到使边缘分布最大化的α和σ。在计算过程中,多出现αi→∞的情况。当μi趋于0,则可以将其对应的基向量删除,令对应的ωi=0,从而得到稀疏化的rvm。考虑到rvm需要计算协方差矩阵∑,计算量比较大,运行时间长,因此本文采用改进后的快速序列稀疏贝叶斯学习算法,计算超参数和噪声方差。
获得超参数值α、σ2后,由于权值最优估计的不确定性,给定任意一个输入值x*,则可得出描述预测不确定度的均值和方差,其中σmp为超参数的最优值,计算公式如下:
y*=μtφ(x*)(6)
在边坡可靠度分析过程中,需首先计算边坡安全系数值。由于边坡安全系数的计算结果受众多因素的影响,各因素的微小浮动均能够引起安全系数值变化,且各因素的取值范围通常较大。因此,边坡安全系数模型应在具有较强的局部插值能力的同时,具有稳定的泛化能力。当前,rvm核函数的类型较多,可分为两类:(1)以高斯核函数为首,插值能力较强的局部核函数,如式(8)所示;(2)以多项式核函数为首,泛化能力较好的全局核函数,如式(9)所示。结合边坡安全系数的计算背景,为使rvm核函数同时具有上述两类核函数的优点,本文建立混合核函数作为rvm核函数,即mrvm,如式(10)所示:
k(x,xi)=exp(-||x-xi||2/c2)(8)
k(x,xi)=[η(x·xi)+r]q(9)
k(x,xi)=mexp(-||x-xi||2/c2)+(1-m)[η(xxi)+r]q(10)
式中,c为高斯核参数;η,r,q为多项式核参数;m为混合核函数的比例参数。
因此,本实施例选定高斯–多项式混合核函数,其在局部差值能力与泛化能力间达到良好的平衡,混合核函数共涉及到5个参数:c,η,r,q,m。后利用hs算法对混合核函数的参数进行寻优,由此建立基于混合核mrvm-afosm的边坡可靠度分析模型。
上述hs算法是模拟作曲家不断调整不同乐器的不同音调,直到生成一个美妙和声的过程,该算法是一种具有全局随机搜索能力的启发式算法,可实现对最优化问题的求解,算法流程如图2所示,其具体步骤为:
(1)初始化参数,主要参数包括:变量个数n、最大迭代次数tmax、和声记忆库的大小hms、记忆库取值概率hmcr、音调微调概率par、音调调节带宽bw,初始化和声记忆库,随机生成hms个和声z1,z2,…,zhms存放至和声记忆库,和声记忆库的和声数量始终保持一定,用于存储适应度f(z1)最优的hms个和声,和声记忆库hm的形式如下:
(2)构建新音调z′i,首先生成一个随机数rand1;若rand1<hmcr,新音调z′i在和声记忆库hm随机取值,后进入步骤(3);若rand1>hmcr,新音调z′i在取值范围内随机取值,后进入步骤(4);
(3)当新音调z′i来自和声记忆库时,则还有par的概率可对该音调进行微调,另有(1-par)的概率保持原值,完成所述微调后,新音调z′i生成,进入步骤(4);
(4)每一个新和声z′中的均由n个新音调z′i(i=1,2,…,n)组成,判断新音调是否全部生成,若没有全部生成,则需重复步骤(2)、(3),直至全部音调生成;
(5)更新和声记忆库,计算新和声的适应度,当其值优于和声记忆库中的适应度最差的和声时,用新和声代替最差和声,完成和声记忆库的更新;
(6)检查是否达到最大迭代次数,并重复步骤(2)~(5),直到迭代次数达到tmax时,计算停止。
hs算法需设定5个参数,其取值较为常规,无需特别设定。采用hs对混合核参数组合进行全局寻优时,应设定混合核参数的变化范围。本文选定的混合核函数共有5个待定参数,其变化范围如表1所示。
表1
在训练过程中,由于mrvm核参数较多,引入hs算法对核参数进行优化,可快速、准确的挑选出适宜的参数组合,大幅度提供mrvm的拟合、预测能力。
步骤三、使用经过训练的mrvm对测试样本的安全系数进行估算,并与步骤一中采用bishop算法对测试样本计算的安全系数比较,计算平均绝对误差(mae);当mae满足误差要求时,核参数值确定,mrvm训练完成,当mae不满足误差要求时,重复步骤二;
步骤四、采用afosm计算可靠度,初始设计验算点采用各影响因子的均值,使用mrvm计算设计验算点的边坡稳定性安全系数及一阶导数,得出新设计验算点;
在边坡可靠性分析的一阶二次矩法中,极限状态方程可以表示为:
z=g(x1,x2,…,xk)=f(x1,x2,…,xk)-1(12)
式中,z为极限状态函数值;g为极限状态函数;f为传统的边坡安全系数计算值;xi(i=1,2,…,k)代表能够对边坡稳定性产生影响的k个随机变量。
边坡处于稳定状态时z>0;边坡处于失稳状态时z<0;z=0表示边坡处于临界状态,位于极限状态面上。设
g(x*)=0(13)
当变量为独立正态随机变量时,线性函数zl的均值μzl、标准差σzl为:
则可靠度指标β为:
引入灵敏度向量αx,其分类
则p*可通过下式计算:
将式(13)、式(17)、式(18)、式(19)联立,即可求解出β和p*。
在实际计算中,直接选定满足式(13)的设计验算点是十分困难的,通常采用迭代法求解:首先假定初始设计验算点,一般取为均值点;然后计算αx、β;计算设计验算点的极限状态函数值,若其值与0相差较大,即不满足式(13),需根据式(19)计算新的设计验算点,重复计算αx、β;若其值与0相差小于允许值,即满足式(13),则终止迭代。
而训练完成后的mrvm可代替bishop算法,对边坡安全系数进行快速、准确计算。因此,极限状态函数值z可以表示为:
式中s为mrvm训练完成后支持向量的个数,即权重wi不为0的训练样本数。
采用afosm求解可靠度时,需求解极限状态函数的一阶导数。mrvm的一阶导数为:
将式(21)代入式(17),其余步骤按上述afsom迭代步骤进行,即可完成可靠度和新设计验算点的求解。
步骤五、如果新设计验算点满足迭代终止条件,则终止迭代,得出边坡可靠度,如果新设计验算点不满足迭代终止条件,则重复步骤四。
此迭代终止准则选为:对于相邻两次计算所得的设计验算点,如果两次设计验算点的相应自变量差值均小于误差允许值,则迭代停止,该误差允许值一般为0.1,本实施例中设置为0.01,当自变量差值小于0.01时,则迭代终止,得出可靠度。自变量为岩石粘聚力c、内摩擦系数
实施例2:
为与rvm-fosm形成对比,本实施例对某单层边坡可靠度进行计算,边坡形态如图3所示,计算主要考虑岩石粘聚力c、内摩擦系数
经过多次试算,最终确定mrvm核参数m=0.9999955、c=9.33294、η=0.46693、r=7.03048、q=1.55978。28组训练数据的平均绝对误差为0.0071,平均相对误差仅为0.47%,拟合效果如图4所示。12组测试数据的平均绝对误差仅为0.0292,平均相对误差仅为1.90%,预测效果如图5所示。因此,mrvm能够准确的估算出边坡的安全系数,有着良好的预测能力,为边坡可靠度计算打下扎实的基础。
不同变异系数下的边坡稳定可靠度计算结果如表2、图6所示,其中fosm、rvm-fosm计算结果采用文献(buchercg,bourgundu.afastandefficientresponsesurfaceapproachforstructuralreliabilityproblems.structsafety1990;7:57–66);geostudio/mcs由geostudio软件进行106次mcs计算得出;afosm、mrvm-afosm均通过matlab程序实现。
表2
mrvm-afosm三次计算所得的设计验算点相近:c=10.11kn/m2、
在每一次迭代过程中,afosm均需采用bishop法计算边坡安全系数,虽耗时较长,但其可靠度计算结果准确,可以作为衡量其他算法准确性的标准。由表2、图6可知:
(1)fosm与rvm-fosm的计算结果相近,但与afosm相比,有明显偏差。其主要原因是这两种均采用了传统的一次二阶矩法,即mvfosm。而mvfosm采用的中心点一般不在极限状态面上,在该点taylor展开的超曲面会明显偏离原极限状态面,使可靠度计算存在明显偏差。
(2)geosudio/mcs、afosm、mrvm-afosm计算结果相近,且geosudio/mcs与mrvm-afosm十分接近。通过106次mcs计算,geosudio软件结果较为准确,但耗时较长。以afosm为标准,本文提出的rvm-afosm的平均绝对误差为0.36,平均相对误差为7.3%,误差较小;
(3)通过多次试验,mrvm-afosm计算的平均耗时为4.3s。同时,mrvm-afosm的可靠度计算结果误差较小,且可靠度偏小,整体偏于安全。因此,针对单层问题,mrvm-afosm计算速度极快,且计算结果较为准确,能够满足实际工程需要。
本文同时对单层边坡采用了高斯核函数进行可靠度计算,计算结果如表3所示。由表可知:高斯核的计算误差明显大于混合核,本文采用混合核进行边坡稳定可靠度计算,精度明显提高。此外,在单层边坡计算中的的混合核比例参数为m=0.9999955,表明高斯核在混合核中占有绝对主导地位,而多项式核函数虽占有比例较小,但其对计算精度的提高效果十分重要。
表3
实施例3:
在上述实施例的基础上,为与svm-fosm形成对比,本实施例对某多层边坡可靠度进行计算,边坡形态见图7。边坡分为三层,各层材料参数见表4,假定自变量均为非相关正态分布。
表4
由于原文章未提供样本,本文将各变量在
mrvm-afosm计算所得的设计验算点为:
表5为各算法对多层边坡可靠度的计算结果。由表5可知:
(1)svm-fosm与pem的计算结果相近,但与afosm相比,有明显偏差。主要原因是svm-fosm采用了传统的一次二阶矩法。陈祖煜指出pem与fosm的计算结果十分接近,计算结果符合此规律。
(2)相比于afosm,geosudio软件结果存在明显误差。
(3)afosm、mrvm-afosm计算结果相近,以afosm为标准,mrvm-afosm的绝对误差为0.045,相对误差为1.19%;mrvm-afosm计算平均耗时为4.8s;mrvm-afosm的可靠度计算结果虽有一定误差,但结果偏小,整体偏于安全。因此,针对多层问题,mrvm-afosm计算速度极快,且计算结果较为准确,能够满足实际工程需要。
表5
同样,本文同时对多层边坡采用了高斯核函数进行可靠度计算,计算结果如表6所示。由此可知:本实施例采用混合核的计算结果更接近真实值,精度提高。此外,在多层边坡计算中的的混合核比例参数为m=0.9999955,表明高斯核在混合核中占有绝对主导地位,而多项式核函数虽占有比例较小,但其对计算精度的提高效果十分重要。
表6
以上内容是结合具体的优选实施方式对本发明所作的进一步详细说明,不能认定本发明的具体实施只局限于这些说明。对于本发明所属技术领域的普通技术人员来说,在不脱离本发明构思的前提下,还可以做出若干简单推演或替换,都应当视为属于本发明的保护范围。
- 还没有人留言评论。精彩留言会获得点赞!