基于改进马尔科夫链的模拟风电功率时间序列生成方法与流程
本发明涉及风电并网规划中的风电功率时间序列模拟领域,是一种基于改进马尔科夫链的模拟风电功率时间序列生成方法。
背景技术:
风力发电的随机性与不确定性使得风电并网后电力系统稳定、安全、可靠运行面临巨大挑战,提高风电功率模拟序列的准确性,在电力系统规划及安全性评估等领域具有重要意义。
模拟生成风电功率时间序列是指以历史风电功率时间序列为基础,生成多个在统计特征上与历史风电功率时间序列相吻合的新序列。
生成风电功率时间序列的方法可分为两类:风速法和风功率法。若以风速时间序列作为输入量,根据风速—功率转换模型生成风电功率时间序列,由于风电场的输出功率还受到地形、温度等其它因素的影响,使风速—功率转换模型很难准确,因此风速法生成的风电功率时间序列较之历史风电功率时间序列存在较大偏差。风功率法是直接利用历史风电功率时间序列进行模拟,避免了经过风速—功率转换模型而进一步造成的偏差;应用马尔科夫链模型并采用风功率法生成的风电功率时间序列,与其它模型生成的风电功率时间序列相比,在概率密度分布与自相关性上表现更好,然而,现有技术的风电功率时间序列方法的原始马尔科夫链模型没有考虑风电功率自身的时域特性,其模拟结果还有待提高。因此需建立一个考虑风电功率特性的基于马尔科夫链的风电功率时间序列模型的基于改进马尔科夫链的模拟风电功率时间序列生成方法。迄今为止,未见有关基于改进马尔科夫链的模拟风电功率时间序列生成方法的文献报道和实际应用。
技术实现要素:
本发明的目的是,提供一种科学合理,简单实用,计算速度快,精度更高,模拟效果更佳的基于改进马尔科夫链的模拟风电功率时间序列生成方法。
实现本发明目的所采用的技术方案是,一种基于改进马尔科夫链的模拟风电功率时间序列生成方法,其特征在于,它包括以下步骤:
1)数据分类
基于改进马尔科夫链的模拟风电功率时间序列生成方法需要综合考虑风电功率的季节特性、日特性及波动特性,因此在计算状态转移矩阵之前需对历史数据进行分类,分类原则如下:
①考虑季节特性
风电功率的季节特性主要表现为一年当中不同月份输出功率的大小存在差异,为了在生成的风电功率时间序列中体现出季节特性,需将时间长度为一年的历史风电功率时间序列分为12个片段,用λ表示,λ=1,2,…,12,每一个月为一个片段;
②考虑日特性
风电功率的日特性主要表现为由于日照的原因,一天当中不同时段风电功率的大小存在差异,且不同月份的日特性一般也不同,需将历史风电功率时间序列每一天的数据分为四部分,每一部分对应的时间分别为00:00-06:00,06:00-12:00,12:00-18:00,18:00-24:00,将四个时间段用θ表示,θ=θ1,θ2,θ3,θ4;
将历史风电功率时间序列用ω来表示,则月份λ里时段θ中的历史风电功率时间序列表示为ωλ.θ,其中λ=1,2,…,12;θ=θ1,θ2,θ3,θ4;
2)确定风电功率状态数
根据历史风电功率区间大小,将风电功率的取值区间平均分为s个部分,s为风电功率状态数;
3)计算风电功率状态转移矩阵
在风电功率的一阶马尔科夫链p={p1,p2,…,pt,…,pn}中,pt为模拟风电功率时间序列中的元素,其中t=1,2,…,n,n为模拟风电功率时间序列的数据个数,风电功率值均处于状态空间e中,e={e1,e2,…,ei,…,es},ei为风电功率的第i个状态,i=1,2,…,s,s为风电功率状态总个数,模拟风电功率时间序列每一时刻的功率值只能处于其中一个状态,风电功率从当前时刻状态转向下一时刻状态的过程称为状态转移,其在状态转移过程中,有s-1种方向是转向其它状态,有一种方向是转向自身,因此每一个状态都有s种转移方向;
状态转移概率的定义为,在t时刻的风电功率值处于状态ei的前提下,t+1时刻的风电功率值处于状态ej的概率,记作fi.j,可用公式(1)计算,
fi.j=g(pt+1∈ej|pt∈ei)(1)
式中,pt和pt+1分别为t时刻和t+1时刻的风电功率值,其中t=1,2,…,n,n为模拟风电功率时间序列的数据个数,ei与ej分别为风电功率的第i个状态和第j个状态,i=1,2,…,s;j=1,2,…,s;s为风电功率状态总个数;g(·|·)为条件转移概率;
状态转移概率矩阵f由状态转移概率构成,如公式(2)所示,为s阶方阵,各行元素之和均为1;
式中,fi.j为风电功率从状态ei转移到状态ej的状态转移概率,i=1,2,…,s;j=1,2,…,s;s为风电功率状态总个数;
在历史风电功率时间序列ωλ.θ中,风电功率从状态ei转移到状态ej的状态转移概率记作fi.j.λ.θ,用公式(3)计算,
式中,ki.j.λ.θ为历史风电功率时间序列ωλ.θ中,风电功率从状态ei转移到状态ej的转移频数,这里只计算经过一步转移的频数,i=1,2,…,s;j=1,2,…,s,s为风电功率状态总个数;
对应风电功率时间序列ωλ.θ的状态转移概率矩阵fλ.θ的表达式见式(4),
式中,fi.j.λ.θ为历史风电功率时间序列ωλ.θ中风电功率从状态ei转移到状态ej的状态转移概率,i=1,2,…,s;j=1,2,…,s;s为风电功率状态总个数,λ=1,2,…,12;θ=θ1,θ2,θ3,θ4;
4)拟合波动量
风电功率的波动性是指后一时刻与当前时刻的风电功率值存在差异,这里采用一阶差分量来刻画波动量,其表达式见公式(5),
δp=pt+1-pt(5)
其中,δp表示风电风功率的波动量;pt+1和pt分别为风电功率时间序列中第t+1时刻和第t时刻的风电功率值,t=1,2,…,n,n为模拟风电功率时间序列的数据个数;
采用tlocation-scale分布函数对风电功率波动量的概率分布函数拟合,其表达式见公式(6),
式中:г的计算公式为
利用公式(6)拟合历史风电功率波动量,得到μ,б,ν的值,然后生成满足公式(6)中所得参数的波动量的集合;
5)模拟生成风电功率时间序列
模拟生成风电功率时间序列的步骤如下:
①确定所用数据的边界
当前时刻记作t,t∈{1,2,…,n},n为模拟风电功率时间序列的数据个数,当前时刻模拟风电功率所处状态记作ei,i∈{1,2,…,s},s为风电功率状态总个数,历史风电功率平均值记作模拟风电功率时间序列开始前的零时刻值,当前时刻风电功率大小记作pt,pt∈(pei.min,pei.max),其中,pei.min、pei.max分别为模拟风电功率状态ei对应的风电功率区间的最小值与最大值,当前时刻风电功率所处月份记作λt,λt∈{1,2,…,12},当前时刻风电功率所处时段记作θt,θt∈{θ1,θ2,θ3,θ4},t∈{1,2,…,n},n为模拟风电功率时间序列的数据个数,生成一个服从均匀分布的随机数ε,且ε∈(0,1);
②计算累计状态转移矩阵
根据已知的λt、θt,确定出对应的状态转移矩阵,进而计算出相应的累计状态转移矩阵qλt.θt,计算公式见式(7),
式中:q为累计状态转移矩阵,qλt.θt为月份λt中时段θt对应的累计状态转移矩阵,fi.δ.t为t时刻风电功率从状态ei转移到状态eδ的状态转移概率,qi.j.t为t时刻风电功率从状态ei转移到状态ej的累计转移概率,δ=1,2,…,j;i=1,2,…,s;j=1,2,…,s;s为风电功率状态总个数,t∈{1,2,…,n},n为模拟风电功率时间序列的数据个数;
③确定下一时刻风电功率状态
求出累计状态转移矩阵后,进一步确定当前模拟风电功率pt的下一时刻模拟风电功率pt+1所处的状态ej,ej∈{e1,e2,…,es},当0<ε<qi.1.t时,j=1,qi.1.t为t时刻的风电功率从状态ei转移到状态e1的累计转移概率;当qi.m.t<ε<qi.m+1.t时,j=m+1,qi.m.t为t时刻的风电功率从状态ei转移到状态em的累计转移概率,qi.m+1.t为t时刻的风电功率从状态ei转移到状态em+1的累计转移概率,em和em+1分别为风电功率的第m个状态和第m+1个状态,m∈{1,2,…,s-1},s为风电功率状态总个数,t∈{1,2,…,n},n为模拟风电功率时间序列的数据个数;
④抽取波动量叠加生成下一时刻风电功率值
确定了当前模拟风电功率pt的下一时刻模拟风电功率pt+1所处状态ej后,进一步确定下一时刻模拟风电功率pt+1的数值,pt+1∈(pej.min,pej.max),pej.min、pej.max分别为状态ej对应的风电功率区间的最小值与最大值,在符合公式(6)的参数的波动值集合中随机抽取波动量γt,γ为风电功率波动值的集合,γ∈(γmin,γmax),γt为t时刻抽取的风电功率波动量,γt∈(γmin,γmax),γmin,γmax分别为风电功率波动值集合的最小值与最大值;
在当前模拟风电功率pt的基础上,叠加当前时刻抽取的风电功率波动量γt,得到下一时刻模拟风电功率pt+1,即pt+1=pt+γt,pt+1∈(pt+γmin,pt+γmax),当pt+1在状态ej的取值范围内时,将pt+1作为模拟风电功率下一时刻的值,否则重新抽取风电功率波动量γt,并重新叠加到pt上,再进行判断,t∈{1,2,…,n},n为模拟风电功率时间序列的数据个数;
⑤判断计算是否结束
当t+1<n时,返回5)模拟生成风电功率时间序列的子步骤②,继续计算下一时刻模拟风电功率值;当t+1=n时,计算过程结束,就生成了所需长度的模拟风电功率时间序列,其中t=1,2,…,n,n为模拟风电功率时间序列的数据个数。
本发明的基于改进马尔科夫链的模拟风电功率时间序列生成方法,在充分利用历史风电功率自身的时域特性的基础上,对基于马尔科夫链的风电功率时间序列模型进行了改进,模拟生成的风电功率时间序列与历史风电功率时间序列及基于马尔科夫链模拟生成的风电功率时间序列相比,在概率密度分布与自相关性方面表现得更好。具有方法科学合理,简单实用,计算速度快,精度更高等优点。
附图说明
图1为本发明的基于改进马尔科夫链的模拟风电功率时间序列生成方法的流程图;
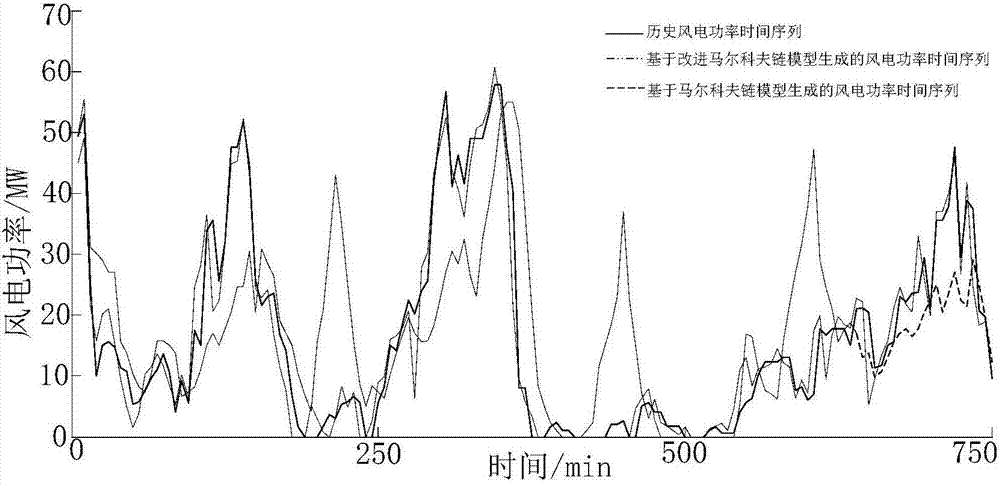
图2为历史风电功率时间序列、基于马尔科夫链模型生成的风电功率时间序列和基于改进马尔科夫链模型生成的风电功率时间序列的曲线;
图3为历史风电功率时间序列、基于马尔科夫链模型生成的风电功率时间序列和基于改进马尔科夫链模型生成的风电功率时间序列的概率分布对比图;
图4为历史风电功率时间序列的自相关系数图;
图5为基于马尔科夫链模型生成的风电功率时间序列的自相关系数图;
图6为基于改进马尔科夫链模型生成的风电功率时间序列的自相关系数图。
具体实施方式
参照图1,本发明的基于改进马尔科夫链的模拟风电功率时间序列生成方法,包括以下步骤:
1)数据分类
需要综合考虑风电功率的季节特性、日特性及波动特性,因此在计算状态转移矩阵之前需对历史数据进行分类,分类原则如下:
①考虑季节特性
风电功率的季节特性主要表现为一年当中不同月份输出功率的大小存在差异,为了在生成的风电功率时间序列中体现出季节特性,需将时间长度为一年的历史风电功率时间序列分为12个片段,用λ表示,λ=1,2,…,12,每一个月为一个片段;
②考虑日特性
风电功率的日特性主要表现为由于日照的原因,一天当中不同时段风电功率的大小存在差异,且不同月份的日特性一般也不同,需将历史风电功率时间序列每一天的数据分为四部分,每一部分对应的时间分别为00:00-06:00,06:00-12:00,12:00-18:00,18:00-24:00,将四个时间段用θ表示,θ=θ1,θ2,θ3,θ4;
将历史风电功率时间序列用ω来表示,则月份λ里时段θ中的历史风电功率时间序列表示为ωλ.θ,其中λ=1,2,…,12;θ=θ1,θ2,θ3,θ4;
2)确定风电功率状态数
根据历史风电功率区间大小,将风电功率的取值区间平均分为s个部分,s为风电功率状态数;
3)计算风电功率状态转移矩阵
在风电功率的一阶马尔科夫链p={p1,p2,…,pt,…,pn}中,pt为模拟风电功率时间序列中的元素,其中t=1,2,…,n,n为模拟风电功率时间序列的数据个数,风电功率值均处于状态空间e中,e={e1,e2,…,ei,…,es},ei为风电功率的第i个状态,i=1,2,…,s,s为风电功率状态总个数,模拟风电功率时间序列每一时刻的功率值只能处于其中一个状态,风电功率从当前时刻状态转向下一时刻状态的过程称为状态转移,其在状态转移过程中,有s-1种方向是转向其它状态,有一种方向是转向自身,因此每一个状态都有s种转移方向;
状态转移概率的定义为,在t时刻的风电功率值处于状态ei的前提下,t+1时刻的风电功率值处于状态ej的概率,记作fi.j,可用公式(1)计算,
fi.j=g(pt+1∈ej|pt∈ei)(1)
式中,pt和pt+1分别为t时刻和t+1时刻的风电功率值,其中t=1,2,…,n,n为模拟风电功率时间序列的数据个数,ei与ej分别为风电功率的第i个状态和第j个状态,i=1,2,…,s;j=1,2,…,s;s为风电功率状态总个数;g(·|·)为条件转移概率;
状态转移概率矩阵f由状态转移概率构成,如公式(2)所示,为s阶方阵,各行元素之和均为1;
式中,fi.j为风电功率从状态ei转移到状态ej的状态转移概率,i=1,2,…,s;j=1,2,…,s;s为风电功率状态总个数;
在历史风电功率时间序列ωλ.θ中,风电功率从状态ei转移到状态ej的状态转移概率记作fi.j.λ.θ,用公式(3)计算,
式中,ki.j.λ.θ为历史风电功率时间序列ωλ.θ中,风电功率从状态ei转移到状态ej的转移频数,这里只计算经过一步转移的频数,i=1,2,…,s;j=1,2,…,s,s为风电功率状态总个数;
对应风电功率时间序列ωλ.θ的状态转移概率矩阵fλ.θ的表达式见式(4),
式中,fi.j.λ.θ为历史风电功率时间序列ωλ.θ中风电功率从状态ei转移到状态ej的状态转移概率,i=1,2,…,s;j=1,2,…,s;s为风电功率状态总个数,λ=1,2,…,12;θ=θ1,θ2,θ3,θ4;
4)拟合波动量
风电功率的波动性是指后一时刻与当前时刻的风电功率值存在差异,这里采用一阶差分量来刻画波动量,其表达式见公式(5),
δp=pt+1-pt(5)
其中,δp表示风电风功率的波动量;pt+1和pt分别为风电功率时间序列中第t+1时刻和第t时刻的风电功率值,t=1,2,…,n,n为模拟风电功率时间序列的数据个数;
采用tlocation-scale分布函数对风电功率波动量的概率分布函数拟合,其表达式见公式(6),
式中:г的计算公式为
利用公式(6)拟合历史风电功率波动量,得到μ,б,ν的值,然后生成满足公式(6)中所得参数的波动量的集合;
5)模拟生成风电功率时间序列
模拟生成风电功率时间序列的步骤如下:
①确定所用数据的边界
当前时刻记作t,t∈{1,2,…,n},n为模拟风电功率时间序列的数据个数,当前时刻模拟风电功率所处状态记作ei,i∈{1,2,…,s},s为风电功率状态总个数,历史风电功率平均值记作模拟风电功率时间序列开始前的零时刻值,当前时刻风电功率大小记作pt,pt∈(pei.min,pei.max),其中,pei.min、pei.max分别为模拟风电功率状态ei对应的风电功率区间的最小值与最大值,当前时刻风电功率所处月份记作λt,λt∈{1,2,…,12},当前时刻风电功率所处时段记作θt,θt∈{θ1,θ2,θ3,θ4},t∈{1,2,…,n},n为模拟风电功率时间序列的数据个数,生成一个服从均匀分布的随机数ε,且ε∈(0,1);
②计算累计状态转移矩阵
根据已知的λt、θt,确定出对应的状态转移矩阵,进而计算出相应的累计状态转移矩阵qλt.θt,计算公式见式(7),
式中:q为累计状态转移矩阵,qλt.θt为月份λt中时段θt对应的累计状态转移矩阵,fi.δ.t为t时刻风电功率从状态ei转移到状态eδ的状态转移概率,qi.j.t为t时刻风电功率从状态ei转移到状态ej的累计转移概率,δ=1,2,…,j;i=1,2,…,s;j=1,2,…,s;s为风电功率状态总个数,t∈{1,2,…,n},n为模拟风电功率时间序列的数据个数;
③确定下一时刻风电功率状态
求出累计状态转移矩阵后,进一步确定当前模拟风电功率pt的下一时刻模拟风电功率pt+1所处的状态ej,ej∈{e1,e2,…,es},当0<ε<qi.1.t时,j=1,qi.1.t为t时刻的风电功率从状态ei转移到状态e1的累计转移概率;当qi.m.t<ε<qi.m+1.t时,j=m+1,qi.m.t为t时刻的风电功率从状态ei转移到状态em的累计转移概率,qi.m+1.t为t时刻的风电功率从状态ei转移到状态em+1的累计转移概率,em和em+1分别为风电功率的第m个状态和第m+1个状态,m∈{1,2,…,s-1},s为风电功率状态总个数,t∈{1,2,…,n},n为模拟风电功率时间序列的数据个数;
④抽取波动量叠加生成下一时刻风电功率值
确定了当前模拟风电功率pt的下一时刻模拟风电功率pt+1所处状态ej后,进一步确定下一时刻模拟风电功率pt+1的数值,pt+1∈(pej.min,pej.max),pej.min、pej.max分别为状态ej对应的风电功率区间的最小值与最大值,在符合公式(6)的参数的波动值集合中随机抽取波动量γt,γ为风电功率波动值的集合,γ∈(γmin,γmax),γt为t时刻抽取的风电功率波动量,γt∈(γmin,γmax),γmin,γmax分别为风电功率波动值集合的最小值与最大值;
在当前模拟风电功率pt的基础上,叠加当前时刻抽取的风电功率波动量γt,得到下一时刻模拟风电功率pt+1,即pt+1=pt+γt,pt+1∈(pt+γmin,pt+γmax),当pt+1在状态ej的取值范围内时,将pt+1作为模拟风电功率下一时刻的值,否则重新抽取风电功率波动量γt,并重新叠加到pt上,再进行判断,t∈{1,2,…,n},n为模拟风电功率时间序列的数据个数;
⑤判断计算是否结束
当t+1<n时,返回5)模拟生成风电功率时间序列的子步骤②,继续计算下一时刻模拟风电功率值;当t+1=n时,计算过程结束,就生成了所需长度的模拟风电功率时间序列,其中t=1,2,…,n,n为模拟风电功率时间序列的数据个数。
实施例的一种基于改进马尔科夫链的模拟风电功率时间序列生成方法,包括以下步骤:
①以西北地区某风电场某一年的风电功率数据作为历史风电功率数据,将历史风电功率的取值区间平均分为40个状态,其中第i个状态对应的风电功率区间为[(i-1),i]×2mw,i=1,2,…,40,历史风电功率平均值记作模拟风电功率时间序列开始前的零时刻值;
②将历史风电功率时间序列按照不同的月份和时段划分成不同的段,并利用公式(3)、公式(4)计算每一类数据对应的状态转移矩阵;
③利用公式(5)计算出历史风电功率时间序列的波动量,采用公式(6)进行拟合,生成满足公式(6)中所得参数的波动量的集合;
④在已计算出的改进马尔科夫链模型的多个状态转移矩阵中,根据模拟风电功率当前时刻所处的月份和时段,确定出对应的状态转移矩阵,并利用公式(7)计算累计状态转移概率矩阵,得出下一时刻模拟风电功率所处的状态,进而确定下一时刻模拟风电功率所在的区间;
⑤在生成的风电功率波动量的集合中随机抽取一个值作为叠加波动量,叠加到当前时刻的风电功率值上,并判断叠加后的风电功率值是否在下一时刻风电功率的范围内,是则继续计算余下时刻的风电功率值,否则重新抽取波动量;
⑥当到下一时刻为止,模拟得到的风电功率时间序列的数据个数为所求风电功率时间序列的数据个数时,停止计算,否则,令时刻值加1后,返回子步骤④;
由于历史风电功率时间序列的时间间隔为5分钟,因此生成的模拟风电功率时间序列也是每隔5分钟的数据,图2为生成的风电功率部分时间序列,为了能够清晰、直观的对比,只给出前750分钟的风电功率时间序列;
⑦将改进马尔科夫链模型和原始马尔科夫链模型生成的风电功率时间序列按不同月份分为12类,分别计算每类的平均值、标准差和最大值,以及各统计参数的绝对误差和相对误差,并与原始风电功率时间序列的各参数值进行对比,结果如表1至表3所示:
表1不同月份的风电功率平均值比较
表2不同月份风电功率标准差比较
表3不同月份风电功率最大值比较
从表1中可看出,改进马尔科夫链模型生成的风电功率时间序列的平均值更接近于原始风电功率时间序列的平均值,且能体现出每个月份风电功率平均值的变化情况,而在原始马尔科夫链模型生成的风电功率时间序列中,每个月的风电功率平均值并没有太大变动,体现不出风电功率的季节特性,由此可得,改进马尔科夫链模型考虑了风电功率季节特性、日特性和波动特性之后,其生成的风电功率时间序列具有更高的精度。表2、表3与表1的分析结果类似。
6)概率密度函数(pdf,probabilitydensityfunction)与自相关系数(acf,(autocorrelationfunction)的比较
将改进马尔科夫链模型和原始马尔科夫链模型生成的风电功率时间序列与历史风电功率时间序列的pdf进行对比,如图3所示,从图3的对比中可得出,改进马尔科夫链模型生成的风电功率序列较好的保留了历史风电功率时间序列的概率分布特性,而原始马尔科夫链模型生成的风电功率序列在概率分布上与历史风电功率时间序列相比相差很大,不能保留历史数据的概率分布特性。
原始风电功率时间序列、原始马尔科夫链模型生成的风电功率时间序列与改进马尔科夫链模型生成的风电功率时间序列,在不同滞后时间下的acf如图4至图6所示。通过比较可以看出,改进马尔科夫链生成的风电功率时间序列基本完全保留了历史风电功率时间序列的自相关性,原始马尔科夫链生成的风电功率时间序列的acf与历史风电功率序列相比相差较大,这是由于风电功率在一年中的不同月份表现出的风电功率特性不同,且在一天当中不同时段的特性也不同,由于改进马尔科夫链模型引入了日特性和季节特性,故生成的风电功率时间序列保留了良好的自相关性。
本发明的特定实施例已对本发明的内容做出了详尽的说明,但不局限本实施例,本领域技术人员根据本发明的启示所做的任何显而易见的改动,都属于本发明权利保护的范围。
- 还没有人留言评论。精彩留言会获得点赞!