临界切除时间的确定方法及装置与流程

本发明涉及电网分析领域，更具体的说，是涉及一种临界切除时间的确定方法及装置。

背景技术：

近年来，随着国家大力推展电网建设，电网规模越来越大，电网系统也越来越复杂，大电网的安全可靠运行，成为本领域技术人员重点研究的课题。电网分析工作中，暂态稳定极限的求取，对电网安全运行具有重要意义。目前对暂态稳定参数分析的主要方法有时域仿真法和直接法。

时域仿真法采用详细模型和逐步积分方法，可得到故障后系统的精确运行轨迹。该方法首先建立系统状态变量的微分方程及网络的代数方程(1)，数学模型包括一次电网的数学描述(网络方程)和发电机、负荷、无功补偿、直流输电等一次设备和二次装置动态特性的数学描述(微分方程)以及各种可能发生的扰动方式和稳定措施的模拟等。然后以某一稳态的潮流计算结果作为初始状态，求解该联立方程组。

其中f＝(f1,f2,...,fn)^t，g＝(g1,g2,......,gn)^t。

x＝(x1,x2,......,xn)^t为微分方程组求解的变量；

y＝(y1,y2,......,yn)^t为网络方程组求解的变量。

采用梯形隐积分的迭代法，求解微分方程；采用直接三角分解和迭代相结合的方法求解网络方程；微分方程和网络方程两者交替迭代，直至收敛，完成一个时段的求解。故障情况下，微分方程具有不连续性，故障引入和故障切除都会引起导纳阵变化，此时需修改系统方程，进行分段求解。

目前，时域仿真法在数学模型、计算方法和程序的实现上已相当成熟，作为一种强有力的离线分析工具，已经被广泛地应用于实际工程中，它的主要优点有：①模型足够精确；②数值稳定性好；③可以作为各种物理问题及控制对策的时域分析方法以及其他分析方法的校验手段。时域仿真法的一些缺点包括：①用于一个大系统进行全过程的暂态稳定分析时，计算工作量大，耗机时间长。②只能判断系统是稳定还是不稳定，无法提供一个连续量化的数值指标；③对于仿真过程中得到的大量信息，利用率较低。

用时域仿真法求取临界切除时间的传统方法，采用二分法逐步搜索的思想，并认为临界切除时间所在的位置即是系统的不返回点。具体流程如下：首先设定初始切除时间，t0＝0s,te＝5s。(将二分法的初始搜索范围设为0-5秒，认为由于继电保护动作以及系统各类调节措施的实施，超出5秒的临界切除时间不影响系统稳定。)然后，判断中间切除时间tm＝(t0+te)/2对应的系统稳定性。暂态稳定判据采用功角判据，设定最大发电机功角差设为500度。若系统稳定则设定t0＝tm；反之，设定te＝tm。如此循环直至t0-te在指定精度范围内。由于初值设置保守，收缩范围较大，采用该方法求取临界切除时间循环次数较多，在大系统分析时将明显降低计算速度。

暂态能量函数法是从能量的观点看问题，而不是通过计算系统运动的轨迹来判断系统是否稳定。pebs法(potentialenergyboundarysurface，势能界面法)，是暂态能量函数法的一种。pebs法假定在不稳定平衡点附近势能变化比较平缓，因此可用持续故障的轨迹与pebs相交的点来求出近似的不稳定平衡点。pebs法对故障轨迹进行模拟跟踪，沿故障轨迹去寻找势能界面，从而确定出系统的临界能量。该方法无需计算相关不稳定平衡点，只要构成相应的暂态能量函数，就可以较方便地计入复杂的元件模型，因此在计及复杂元件模型进行直接法暂态稳定分析时，被广泛采用。

对于含有n台发电机的电力系统，假定发电机采用经典二阶模型；发电机的输入机械功率保持恒定；负荷用恒定阻抗模拟；忽略系统阻尼。由于在同步坐标下进行暂态稳定直接法分析往往精度很差，实际分析通常采用惯量中心坐标系(centerofinertia，coi)进行分析。

惯量中心(coi)的等值转子角δcoi定义为各发电机转子角δi的加权平均值，权系数为mi，即发电机的惯性时间常数，从而：

式中

惯量中心等值角速度ωcoi定义为：

式中ωi为各发电机转子角速度与同步速的偏差。显然有

定义coi坐标下各发电机的转子角和转子角速度为：

对于i＝1,2...n，将各发电机运动方程作累加，并根据惯量中心的定义，可导出惯量中心的运动方程为：

pcoi为coi坐标下的加速功率，其值等于各发电机加速功率之和。

(1)coi坐标下n机系统的数学模型

对于第i台发电机，将代入

根据惯量中心的运动方程，可得：

另外可导出

因此，coi坐标下各发电机的运动方程为：

由于系统采用经典模型，可以将网络收缩到发电机内节点，上式中

其中θij＝θi-θj＝(δi-δcoi)-(δj-δcoi)＝δij，yij＝gij+jbij,yij为收缩到发电机内节点的节点导纳阵，gij为节点i的自电导，gij为节点i、j的互电导，bij为节点i、j的互电纳。

(2)coi坐标下的暂态能量

暂态动能：

暂态势能：

系统的暂态能量为：

暂态能量函数法的主要优点在于：①计算速度快；②可以通过能量判据来判别稳定，并给出稳定裕度。虽然暂态能量函数法已趋于成熟，但在实际应用中仍然存在着许多缺点和局限性，主要有：①对模型的适应性有待于进一步提高；②分析得到的结果只能提供系统动态过程的特性和一些有价值的信息，不能提供系统变量的时间响应；③如果系统不稳定，暂态能量函数法的分析不能指明系统是如何失步的，也不能指明被解列的那部分系统是否免遭破坏；④不能反映有切换操作的系统的稳定性。目前，暂态能量函数法还处在不断发展之中。

综上所述，如何提供一种有效的故障临界切除时间的确定方法，是本领域技术人员亟待解决的问题。

技术实现要素：

有鉴于此，本发明提供了一种临界切除时间的确定方法及装置，以实现对故障临界切除时间的快速而精确的获取。

为实现上述目的，本发明提供如下技术方案：

一种临界切除时间的确定方法，包括：

通过直接法计算确定临界切除时间初值tcr；

根据所述临界切除时间初值tcr和时域仿真系统误差error确定搜索范围；

在所述搜索范围内，采用二分法搜索并确定临界切除时间cct。

可选的，所述直接法为pebs法，则所述通过直接法计算确定临界切除时间初值tcr，包括：

通过pebs法计算临界切除时间初值tcr。

可选的，所述根据所述临界切除时间初值tcr和时域仿真系统误差error确定搜索范围，包括：

确定故障极限时间初值min＝tcr*(1-error),max＝tcr*(1+error)，并将[min，max]确定为搜索范围。

可选的，所述在所述搜索范围内，采用二分法搜索并确定临界切除时间cct，包括：

计算初始潮流；

确定时域仿真法的计算步长dt；

确定故障开始时间为ts＝min，故障结束时间为te＝(min+max)/2；

通过时域仿真法进行暂态稳定计算；

通过二分法确定最小区间，所述最小区间满足max-min＜dt；

根据所述最小区间确定临界切除时间cct。

可选的，所述通过时域仿真法进行暂态稳定计算，包括：

通过梯形隐积分的迭代法，求解微分方程；

通过直接三角分解和迭代相结合的方法求解网络方程；

将所述微分方程和所述网络方程进行交替迭代处理，直至收敛。

一种临界切除时间的确定装置，包括：

初值确定模块，用于通过直接法计算确定临界切除时间初值tcr；

范围确定模块，用于根据所述临界切除时间初值tcr和时域仿真系统误差error确定搜索范围；

cct确定模块，用于在所述搜索范围内，采用二分法搜索并确定临界切除时间cct。

可选的，所述直接法为pebs法，则所述初值确定模块具体用于：

通过pebs法计算临界切除时间初值tcr。

可选的，所述范围确定模块具体用于：

确定故障极限时间初值min＝tcr*(1-error),max＝tcr*(1+error)，并将[min，max]确定为搜索范围。

可选的，所述cct确定模块包括：

潮流计算模块，用于计算初始潮流；

步长确定模块，用于确定时域仿真法的计算步长dt；

时间设置模块，用于确定故障开始时间为ts＝min，故障结束时间为te＝(min+max)/2；

暂态计算模块，用于通过时域仿真法进行暂态稳定计算；

区间确定模块，用于通过二分法确定最小区间，所述最小区间满足max-min＜dt；

时间确定模块，用于根据所述最小区间确定临界切除时间cct。

可选的，所述暂态计算模块具体用于：

通过梯形隐积分的迭代法，求解微分方程；通过直接三角分解和迭代相结合的方法求解网络方程；将所述微分方程和所述网络方程进行交替迭代处理，直至收敛。

经由上述的技术方案可知，与现有技术相比，本发明公开了一种临界切除时间的确定方法及装置，首先通过直接法计算确定临界切除时间初值tcr，然后根据所述临界切除时间初值tcr和时域仿真系统误差error确定搜索范围，在所述搜索范围内，采用二分法搜索并确定临界切除时间cct。所述临界切除时间的确定方法及装置，以直接法的计算结果为初值，基于该初值，用时域仿真法进行精确搜索，在提升计算速度的同时，保证了临界切除时间结果的准确性。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据提供的附图获得其他的附图。

图1为本发明实施例公开的临界切除时间的确定方法流程图；

图2为本发明实施例公开的确定临界切除时间cct的流程图；

图3为本发明实施例公开的临界切除时间的确定装置的结构示意图；

图4为本发明实施例公开的cct确定模块的结构示意图。

具体实施方式

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

请参阅附图1，为本发明公开的临界切除时间的确定方法流程图，如图1所示，所述方法可以包括：

步骤101：通过直接法计算确定临界切除时间初值tcr。

其中，临界切除时间tcr是指能使系统保持暂态稳定的最大切除时间。暂态稳定指的是电力系统受到大干扰后，各发电机保持同步运行并过渡到新的或恢复到原来稳定运行状态的能力。临界切除时间具有表征系统暂态稳定性的能力。一般地，临界切除时间越大，表征系统抵御故障的能力越强。相应地，系统的稳定裕度越大；反之系统稳定裕度越小。

具体的，通过直接法计算确定临界切除时间初值tcr，可以包括：通过pebs法，即势能界面法，来计算临界切除时间初值tcr。由于采用pebs法计算临界切除时间在实际应用中已实现，在此不再详细介绍。

步骤102：根据所述临界切除时间初值tcr和时域仿真系统误差error确定搜索范围。

具体的，步骤102可以包括：确定故障极限时间初值min＝tcr*(1-error),max＝tcr*(1+error)，并将[min，max]确定为搜索范围。

故障切除时间是指从故障发生起至故障元件完全从电网切除的这段时间。上面所述的故障极限时间min，可以理解为故障切除时间的最小值，故障极限时间max，可以理解为故障切除时间的最大值。

步骤103：在所述搜索范围内，采用二分法搜索并确定临界切除时间cct。

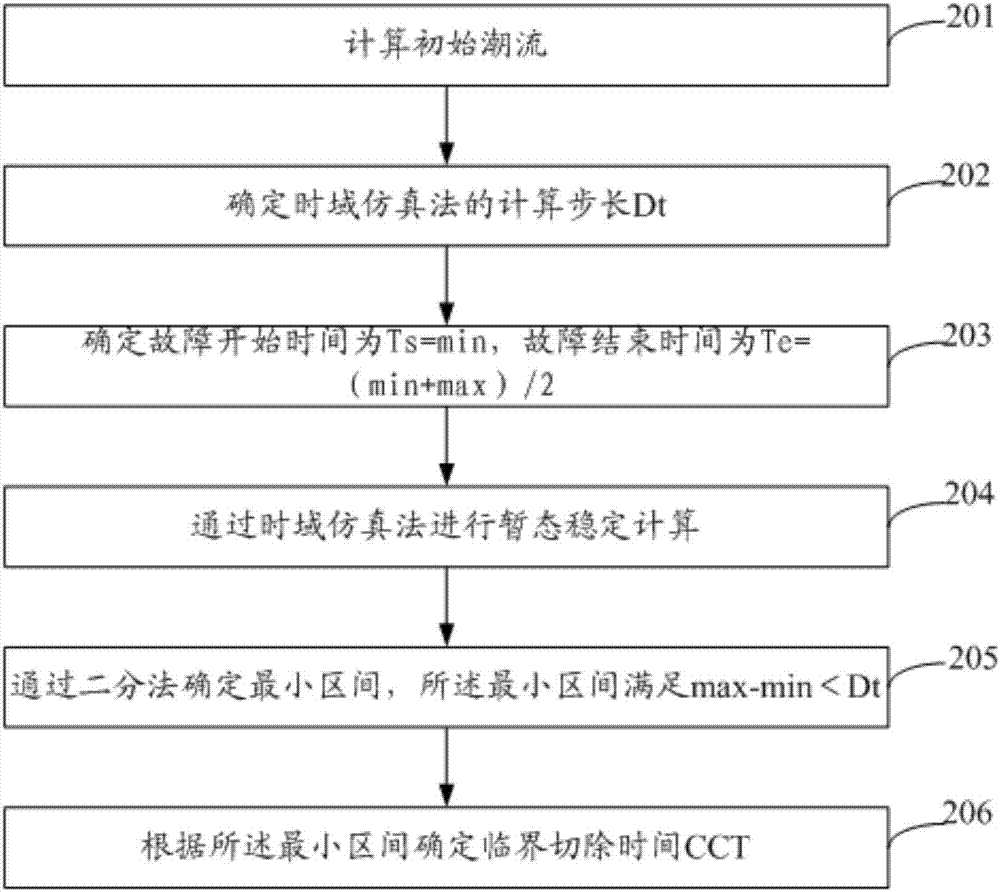
图2为本发明实施例公开的确定临界切除时间cct的流程图，如图2所示，可以包括：

步骤201：计算初始潮流；

步骤202：确定时域仿真法的计算步长dt；

步骤203：确定故障开始时间为ts＝min，故障结束时间为te＝(min+max)/2；

步骤204：通过时域仿真法进行暂态稳定计算；

首先建立系统状态变量的微分方程及网络的代数方程：

其中，其中f＝(f1,f2,...,fn)^t，g＝(g1,g2,......,gn)^t。

x＝(x1,x2,......,xn)^t为微分方程组求解的变量；

y＝(y1,y2,......,yn)^t为网络方程组求解的变量。

结合上面所述的初始潮流结果、步长dt、故障开始时间和故障结束时间求解上述方程。

具体的，可以通过梯形隐积分的迭代法，求解微分方程；通过直接三角分解和迭代相结合的方法求解网络方程；将所述微分方程和所述网络方程进行交替迭代处理，直至收敛，完成一个时段的求解。故障情况下，微分方程具有不连续性，故障引入和故障切除都会引起导纳阵变化，此时需修改系统方程，进行分段求解。系统方程是一个潮流计算的初始值，可以理解为一个假设值，上面所述修改系统方程，即是修改初始值的数字。

步骤205：通过二分法确定最小区间，所述最小区间满足max-min＜dt；

其中，可以将最小区间，即积分区间max-min小于积分步长dt设置为搜索终止条件，从而保证最后的结果与时域仿真法的精度相符合。

步骤206：根据所述最小区间确定临界切除时间cct。

具体的，在采用二分法确定临界切除时间cct的过程中，可以根据一次计算结束时最小区间两端点max、min处的稳定情况判断计算是否成功：若两时间点处系统都稳定则cct计算失败，重新设置计算区间min＝max；max＝5；若两时间点处系统都失稳则cct计算失败，重新设置计算区间min＝0；max＝min；若max处系统失稳，min处系统稳定则计算成功。

表1为华东电网500kv网架cct计算结果，其中混合法即为本发明实施例公开的临界切除时间的确定方法。结合表1，华东电网包括江苏、浙江、福建、安徽和上海电网，含176个500kv电压级节点。由于500kv母线均为重要母线，因此对所有176条母线进行故障扫描，仿真结果如表1所示。

表1：华东电网500kv网架cct计算结果

表1中列出了临界时间最小的前10个故障母线，并对比分析了直接法和混合法的计算精度。从表中可以看出故障情况最严重的前十条母线中，只有浙双龙线的直接法结果误差范围超出了20％，也就是说只有一条母线需要二次搜索。另外，根据混合法的计算原理，其计算结束的条件与时域仿真法一致，因此混合法的结果的精度与时域仿真法的精度一致。

表2：华东电网500kv网架cct求解时间

表2为华东电网500kv网架仿真计算时间。表2中比较了传统时域仿真方法和混合法分析华东电网500kv网架所用的时间。由于减少了搜索的范围，计算cct所需的暂态稳定计算次数减少，仿真表明采用混合法可节省约2/3的时间。

本实施例中，所述临界切除时间的确定方法首先通过直接法计算确定临界切除时间初值tcr，然后根据所述临界切除时间初值tcr和时域仿真系统误差error确定搜索范围，在所述搜索范围内，采用二分法搜索并确定临界切除时间cct。所述临界切除时间的确定方法，以直接法的计算结果为初值，基于该初值，用时域仿真法进行精确搜索，在提升计算速度的同时，保证了临界切除时间结果的准确性。

上述本发明公开的实施例中详细描述了方法，对于本发明的方法可采用多种形式的装置实现，因此本发明还公开了一种装置，下面给出具体的实施例进行详细说明。

图3为本发明实施例公开的临界切除时间的确定装置的结构示意图，如图3所示，所述临界切除时间的确定装置30可以包括：

初值确定模块301，用于通过直接法计算确定临界切除时间初值tcr；

其中，临界切除时间tcr是指能使系统保持暂态稳定的最大切除时间。暂态稳定指的是电力系统受到大干扰后，各发电机保持同步运行并过渡到新的或恢复到原来稳定运行状态的能力。临界切除时间具有表征系统暂态稳定性的能力。一般地，临界切除时间越大，表征系统抵御故障的能力越强。相应地，系统的稳定裕度越大；反之系统稳定裕度越小。

具体的，所述初值确定模块301具体可以用于：通过pebs法，即势能界面法，来计算临界切除时间初值tcr。由于采用pebs法计算临界切除时间在实际应用中已实现，在此不再详细介绍。

范围确定模块302，用于根据所述临界切除时间初值tcr和时域仿真系统误差error确定搜索范围；

具体的，所述范围确定模块302可以用于：

确定故障极限时间初值min＝tcr*(1-error),max＝tcr*(1+error)，并将[min，max]确定为搜索范围。

故障切除时间是指从故障发生起至故障元件完全从电网切除的这段时间。上面所述的故障极限时间min，可以理解为故障切除时间的最小值，故障极限时间max，可以理解为故障切除时间的最大值。

cct确定模块303，用于在所述搜索范围内，采用二分法搜索并确定临界切除时间cct。

图4为本发明实施例公开的cct确定模块的结构示意图，如图4所示，所述cct确定模块303可以包括：

潮流计算模块401，用于计算初始潮流；

步长确定模块402，用于确定时域仿真法的计算步长dt；

时间设置模块403，用于确定故障开始时间为ts＝min，故障结束时间为te＝(min+max)/2；

暂态计算模块404，用于通过时域仿真法进行暂态稳定计算；

首先建立系统状态变量的微分方程及网络的代数方程：

其中，其中f＝(f1,f2,…,fn)^t，g＝(g1,g2,......,gn)^t。

x＝(x1,x2,......,xn)^t为微分方程组求解的变量；

y＝(y1,y2,......,yn)^t为网络方程组求解的变量。

结合上面所述的初始潮流结果、步长dt、故障开始时间和故障结束时间求解上述方程。

具体的，可以通过梯形隐积分的迭代法，求解微分方程；通过直接三角分解和迭代相结合的方法求解网络方程；将所述微分方程和所述网络方程进行交替迭代处理，直至收敛，完成一个时段的求解。故障情况下，微分方程具有不连续性，故障引入和故障切除都会引起导纳阵变化，此时需修改系统方程，进行分段求解。系统方程是一个潮流计算的初始值，可以理解为一个假设值，上面所述修改系统方程，即是修改初始值的数字。

区间确定模块405，用于通过二分法确定最小区间，所述最小区间满足max-min＜dt；

其中，可以将最小区间，即积分区间max-min小于积分步长dt设置为搜索终止条件，从而保证最后的结果与时域仿真法的精度相符合。

时间确定模块406，用于根据所述最小区间确定临界切除时间cct。

具体的，在采用二分法确定临界切除时间cct的过程中，可以根据一次计算结束时最小区间两端点max、min处的稳定情况判断计算是否成功：若两时间点处系统都稳定则cct计算失败，重新设置计算区间min＝max；max＝5；若两时间点处系统都失稳则cct计算失败，重新设置计算区间min＝0；max＝min；若max处系统失稳，min处系统稳定则计算成功。

本实施例中，所述临界切除时间的确定装置首先通过直接法计算确定临界切除时间初值tcr，然后根据所述临界切除时间初值tcr和时域仿真系统误差error确定搜索范围，在所述搜索范围内，采用二分法搜索并确定临界切除时间cct。所述临界切除时间的确定装置，以直接法的计算结果为初值，基于该初值，用时域仿真法进行精确搜索，在提升计算速度的同时，保证了临界切除时间结果的准确性。

本说明书中各个实施例采用递进的方式描述，每个实施例重点说明的都是与其他实施例的不同之处，各个实施例之间相同相似部分互相参见即可。对于实施例公开的装置而言，由于其与实施例公开的方法相对应，所以描述的比较简单，相关之处参见方法部分说明即可。

还需要说明的是，在本文中，诸如第一和第二等之类的关系术语仅仅用来将一个实体或者操作与另一个实体或操作区分开来，而不一定要求或者暗示这些实体或操作之间存在任何这种实际的关系或者顺序。而且，术语“包括”、“包含”或者其任何其他变体意在涵盖非排他性的包含，从而使得包括一系列要素的过程、方法、物品或者设备不仅包括那些要素，而且还包括没有明确列出的其他要素，或者是还包括为这种过程、方法、物品或者设备所固有的要素。在没有更多限制的情况下，由语句“包括一个……”限定的要素，并不排除在包括所述要素的过程、方法、物品或者设备中还存在另外的相同要素。

结合本文中所公开的实施例描述的方法或算法的步骤可以直接用硬件、处理器执行的软件模块，或者二者的结合来实施。软件模块可以置于随机存储器(ram)、内存、只读存储器(rom)、电可编程rom、电可擦除可编程rom、寄存器、硬盘、可移动磁盘、cd-rom、或技术领域内所公知的任意其它形式的存储介质中。

对所公开的实施例的上述说明，使本领域专业技术人员能够实现或使用本发明。对这些实施例的多种修改对本领域的专业技术人员来说将是显而易见的，本文中所定义的一般原理可以在不脱离本发明的精神或范围的情况下，在其它实施例中实现。因此，本发明将不会被限制于本文所示的这些实施例，而是要符合与本文所公开的原理和新颖特点相一致的最宽的范围。