基于典型相关性分析及线性插值的土壤养分模型转移方法与流程

本发明涉及一种模型转移方法，具体涉及基于典型相关性分析及线性插值的土壤养分模型转移方法。

背景技术：

光谱中包含丰富的物质信息，且光谱分析技术具有无损、快速等优点，在农业、食品、工业等领域已有广泛的应用。采用光谱数据以及相关化学值进行建模，能够快速实现对未知样品化学值的预测，但这种光谱模型对未知样品的预测具有一定的局限性，只能够针对一定范围内的未知样品进行预测。不同温度、不同仪器、不同测量条件、不同地区间样品的光谱均会导致预测结果不准确。为解决这一问题，一种方法是采集样品光谱及化学值重新建立模型，该方法耗时耗力；另一种方法对原模型进行模型转移解决模型不适配等问题，简单、快速的提高未知样品的预测结果。

针对不同温度、不同仪器、不同测量条件下的模型转移主要采用直接校正法(ds)、分段直接校正(pds)、正交信号法(osc)、小波变换(wt)、专利算法(shenk's)等算法，在一定程度上能解决模型受仪器性能变化、分析时间、测量条件等方面的影响。针对不同地区间样品的模型转移主要为添加新样本于原模型中，重新建立模型，这种方法不仅耗时，同时修订后的模型预测效果会降低，不能够实现对不同地区间未知样品的准确预测。目前基于光谱技术针对不同地区间土壤养分进行模型转移尚没有成熟的算法较好的预测结果，因此提供一种快速、准确实现不同地区间土壤养分模型转移方法是很有必要的。

技术实现要素：

本发明为解决不同地区间土壤养分模型转移的问题，采用以下述技术方案予以实现：

基于典型相关性分析及线性插值的土壤养分模型转移方法，步骤如下：

(1)采集某一地区土壤样品，测得其光谱数据和养分化学值，并将该土壤样品作为主样品，用于主样品模型的建立；

(2)采集其他地区土壤样品，采用与主样品同样的光谱仪测得其光谱数据和养分化学值，将其作为从样品，用于对主样品模型的预测；

(3)采用kennard-stone算法划分土壤主样品的校正集和检验集；以偏最小二乘法(pls)建立主样品校正集模型，并对主样品检验集进行预测，根据绝对系数r²和相对分析误差rpd判断主样品模型效果；

(4)采用kennard-stone算法划分土壤从样品的标准集和未知集，其中标准集用于主样品校正集模型转移的标准样品，未知集用于检验模型转移后土壤样品的预测结果；

(5)对主样品建模集和检验集及从样品标准集和未知集进行光谱预处理；

(6)分别采用多种算法对从样品进行模型转移，代入原主样品校正模型，得到土壤从样品未知集的预测结果；

(7)对从样品未知集化学值和预测值进行评价分析，推荐出效果最好的模型转移算法，将此算法用于该从样品地区土壤的样品预测，用校准后的模型进行大批量速测。

步骤(1)、(2)中，采用可见-近红外光谱、近红外光谱等光谱数据。

步骤(1)、(2)中，测量全氮、全磷、全钾等土壤养分含量。

步骤(5)中，光谱预处理包括无预处理、谱区选择、平滑求导、snv、msc、归一化等。

步骤(6)中，多算法包括分段直接矫正结合线性插值(pds-li)、直接矫正结合线性插值(ds-li)、典型相关性分析结合线性插值(cca-li)、分段直接矫正结合斜率/截距修正法(pds-s/b)、直接矫正结合斜率/截距修正法(ds-s/b)、典型相关性分析结合斜率/截距修正法(cca-s/b)等算法。

步骤(6)中，典型相关性分析结合线性插值(cca-li)算法具体步骤为：

1)采用cca算法求出转移矩阵f。采用kennard-stone算法从主样品校正集x主中筛选出与从样品标准集x标样品个数一样的矩阵x主cca，根据x主cca和x标计算矩阵c,由矩阵c计算特征值与特征向量，其相关公式如下：

将每一个非零特征值ρ所对应的特征向量wm和ws分别归为矩阵wm和ws，即为x主cca和x标的典型相关系数wm和ws，对x主cca和x标进行cca分解，计算出x主cca和x标的典型相关成分lm和ls，最终得到转移矩阵f，公式如下：

lm＝x主cca×wm

ls＝x标×ws

f＝ws×f1×f2

2)根据转移矩阵f，分别对从样品标准集x标和未知集x未光谱进行转换，得到经cca算法转换后的标准集x标f和未知集x未f相关公式如下：

x标f＝x标·f

x未f＝x未·f

3)建立预测值校正函数。用主模型分别对从样品标准集和未知集转化后的光谱矩阵进行预测。分别计算标准集中每个样品与未知集中的第i个样品的共生距离d(i)，共生距离d(i)为转化光谱的欧氏距离与化学预测值的绝对偏差之和，计算公式为：

d2(p,i)＝|y标f(p)-y未f(i)|

其中，m为光谱波长点数，x标f和x未f分别为标准集和未知集的转换后的光谱矩阵，y标f和y未f分别为标准集和未知集经转换矩阵f转换后的预测值，d1(p,i)为标准集中第p个样品与未知集中第i个样品之间光谱的欧式距离，d2(p,i)为标准样品中第p个样品与未知样品中第i个样品之间预测值的绝对值偏差，d1(i)和d2(i)分别为d1(p,i)和d2(p,i)中p取1-n所有值组成的向量，n为标准集的样品个数。

寻找d(i)中2个最小值对应的序列p1和p2，根据标准集中的第p1、p2个样品对应的预测值和实测值，建立插值函数。将未知集中第i个样品的预测值代入插值函数，得到校正后的预测值y未p，相关公式如下：

其中，y标(p1)和y标(p2)为标准集养分含量的实测值。

步骤(6)中，分段直接矫正结合斜率/截距修正法(pds-s/b)算法具体步骤为：

1)采用pds算法求出转移矩阵f。分别计算主样品校正集x主和从样品标准集x标的平均光谱，对主样品第j个波长点处的光谱值求其平均光谱m1，在从样品标准集平均光谱m2的第j个波长点附近截取窗口宽度为(j-k～j+k)的波段，令zj＝[m2,j-k,…,m2,j,m2,j+1,…m2,j+k]，然后构建m1(j)与zj之间的多元线性回归方程m1(j)＝zj×fj，由pls算法求得回归系数fj，然后循环j，求出所有的fj。将fj置于转移矩阵f的主对角线上，并将其他元素置0，得到转移矩阵f，相关公式如下：

m1＝m2·f

其中，n1和n2分别为x主和x标的样品个数，x(i,j)为光谱矩阵x中第i行第j列处的光谱值。

2)根据转移矩阵f，分别对从样品标准集x标和未知集x未光谱进行转换，得到经pds算法转换后的标准集x标f和未知集x未f相关公式如下：

x标f＝x标·f

x未f＝x未·f

3)采用s/b算法计算最终预测值，用一元线性回归方程来拟合转换后的标准集x标f和转换后标准集的实测值y标，求得此线性方程的最小二乘解，即为该线性模型的斜率slope和截距bias，根据计算的斜率和截距求得未知集的预测值y未p，相关公式如下：

y未p＝slope·x未f+bias

步骤(6)中，典型相关性分析结合斜率/截距修正法(cca-s/b)算法具体步骤为：

1)采用cca算法求出转移矩阵f。采用kennard-stone算法从主样品校正集x主中筛选出与从样品标准集x标样品个数一样的矩阵x主cca，根据x主cca和x标计算矩阵c,由矩阵c计算特征值与特征向量，其相关公式如下：

将每一个非零特征值ρ所对应的特征向量wm和ws分别归为矩阵wm和ws，即为x主cca和x标的典型相关系数wm和ws，对x主cca和x标进行cca分解，计算出x主cca和x标的典型相关成分lm和ls，最终得到转移矩阵f，公式如下：

lm＝x主cca×wm

ls＝x标×ws

f＝ws×f1×f2

2)根据转移矩阵f，分别对从样品标准集x标和未知集x未光谱进行转换，得到经cca算法转换后的标准集x标f和未知集x未f相关公式如下：

x标f＝x标·f

x未f＝x未·f

3)采用s/b算法计算最终预测值，用一元线性回归方程来拟合转换后的标准集x标f和转换后标准集的实测值y标，求得此线性方程的最小二乘解，即为该线性模型的斜率slope和截距bias，根据计算的斜率和截距求得未知集的预测值y未p，相关公式如下：

y未p＝slope·x未f+bias

基于不同品种或地区间的模型转移现有算法有分段直接矫正结合线性插值(pds-li)、直接矫正结合线性插值(ds-li)、斜率/截距修正法(s/b)、直接矫正结合斜率/截距修正法(ds-s/b)等。分段直接矫正结合线性插值(pds-li)算法是采用pds算法对从样品进行校正，然后在从样品标准样品中选择与未知样品最接近的两个样品，根据其预测值和实测值，建立li函数，实现对未知样品的预测。直接矫正结合线性插值(ds-li)与pds-li算法类似，区别在于采用ds算法对从样品进行校正，然后再建立li函数。斜率/截距修正法(s/b)算法是主样品模型对从样品标准集的预测值和实测值用一条直线拟合得到斜率和截距，将其作为模型转移未知样品修正的系数。直接矫正结合斜率/截距修正法(ds-s/b)是先对从样品进行ds校正，然后采用s/b算法得到模型转移未知样品的修正系数。这些算法也可用于本技术方案。

步骤(7)中，评价分析采用平均相对误差、最大相对误差、预测均方根误差(rmsep)综合进行评价分析。

本发明基于光谱技术，采用多种模型转移算法，实现不同地区间土壤的养分含量值预测。在现有仪器间模型转移算法应用的基础上，通过结合和改进现有模型转移算法，提出一些新的模型转移算法，如pds-s/b、cca-li、cca-s/b等，将其作为多算法推荐的基础。通过采用多种模型转移算法实现不同地区间土壤养分含量的预测，根据平均相对误差、预测均方根误差等评价标准推荐出一种最优模型转移方法，能够更加全面、准确的实现土壤养分含量的预测。本发明运用一个土壤养分含量模型，提出了新的模型转移算法，结合多种模型转移算法推荐出最优算法，解决了不同地区间土壤养分含量预测的难题，在保证该模型预测效果的同时，减少了土壤养分化学方法测量的时间，降低成本，节省人力物力，快速、简单的实现土壤养分的预测。

附图说明

图1：基于典型相关性分析及线性插值的土壤养分模型转移方法流程图；

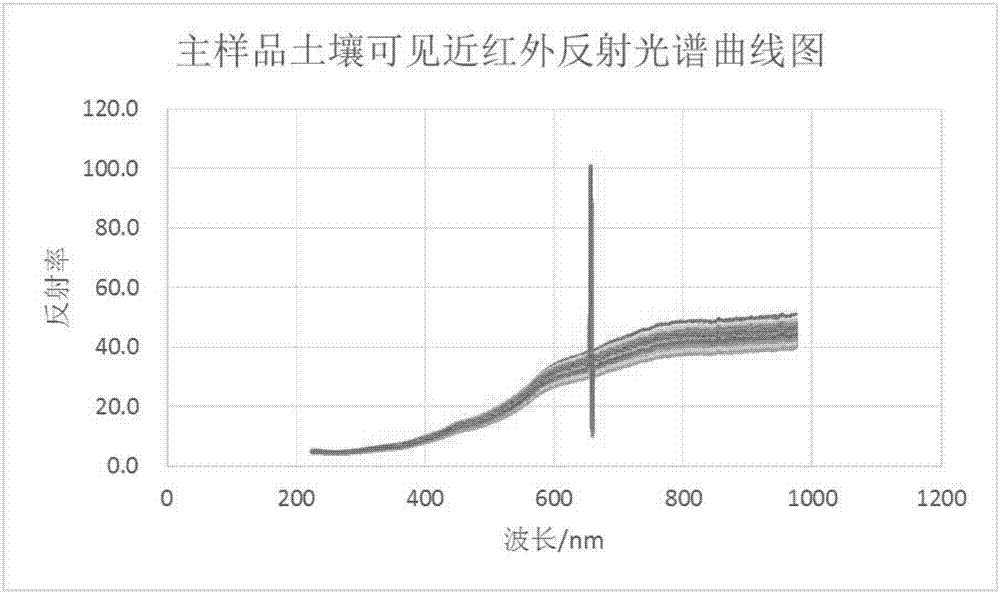
图2：主样品土壤可见近红外反射光谱曲线图；

图3：从样品土壤可见近红外反射光谱曲线图；

图4：主样品与从样品第一主成分和第二主成分空间分布图；

图5：主样品土壤养分(全氮)校正集的拟合结果图；

图6：主样品土壤养分(全氮)检验集的拟合结果图；

图7：从样品未知集土壤养分(全氮)预测值与实测值对比图。

具体实施方式

结合附图和具体实施方式对本发明的技术方案作进一步详细的说明：

基于典型相关性分析及线性插值的土壤养分模型转移方法，采用cca-li算法对不同地区间土壤全氮含量值实现模型转移为例，包括下列步骤：

(1)采集土壤样品

采集青岛浮山山麓、青岛李村河畔土壤样品各60份，深度为0-20cm，设定青岛李村河畔土壤为主样品，设定青岛浮山山麓为从样品。

(2)测定土壤样品养分含量及可见-近红外光谱

从土壤样品中分别取出5-10g，采用碳氮分析仪测定土壤样品的全氮含量。

采用海洋光学qe65000光谱仪测定土壤样品的光谱，谱区范围是200-1100nm(光谱范围主要为可见近红外光谱，包含小部分紫外光谱)。每个土壤样品测定5次光谱反射率，取平均值，主、从样品土壤可见近红外反射光谱的曲线图分别如图2、图3所示.主、从样品土壤第一主成分与第二主成分在主成分空间的分布见图4，主、从样品在主成分空间中分成了两个区域，说明两样品光谱有明显差异。

(3)建立主样品校正模型

采用kennard-stone算法以3:1的比例划分主样品的校正集和检验集，即校正集45份，检验集15份。以偏最小二乘法(pls)建立主样品校正集模型，并对主样品检验集进行预测，主样品土壤养分(全氮)校正集和检验集的拟合结果分别如图5、图6所示,校正集和检验集的绝对系数r²分别为0.9603、0.9053，相对分析误差rpd为2.506。该模型校正集和检验集的绝对系数均在0.9以上，且rpd值在2.5以上，该校正模型预测效果极好。

(4)划分从样品标准集和未知集

剔除从样品中的异常土壤样品，采用kennard-stone算法以1:5的比例划分从样品的标准集和未知集，即标准集10份，未知集48份。

(5)光谱预处理和模型转移

主、从样品无光谱预处理，采用cca-li算法对主、从样品进行模型转移，下表为未经模型转移预测结果、进行模型转移后预测结果及其相对误差，图7为未知集土壤养分(全氮)预测值与实测值对比图。

由上表可知，经cca-li模型转移算法处理后，预测值准确性有大幅度的提高，无模型转移平均相对误差为462.9％，模型转移后平均相对误差为8.51％，平均相对误差明显下降；模型转移后相对误差最大值为21.36％，远小于无模型转移每个预测值与实测值的相对误差；rmsep由2.525降为0.053，因此采用cca-li算法能够实现不同地区间土壤养分含量预测。

以上实施例仅用以说明本发明的技术方案，而非对其进行任何限制；尽管参照前述实施例对本发明进行了详细的说明，对于本领域的普通技术人员来说，依然可以对前述实施例所记载的技术方案进行修改，或者对其中部分技术特征进行等同替换；而这些修改或替换，并不使相应技术方案的本质脱离本发明所要求保护的技术方案的精神和范围。