一种基于位置社交网络的商家推荐的优化方法与流程
本发明属于位置社交网络技术领域,具体涉及一种基于位置社交网络的商家推荐的优化方法。
背景技术:
位置社交网络的广泛使用与其规模的不断扩大使得商家推荐系统成为时下热门应用之一。商家推荐系统即为用户推荐可能感兴趣地点的商家。位置社交网络中存在着丰富的多源异构信息,如社交网络关系,包含经纬度的地理位置信息,用户对商家的点评文本,评分以及相应的时间戳信息等。母庸置疑,通过挖掘这些信息可以有效提升个性化商家推荐系统的准确性。
传统的推荐系统方法可以被无缝地移值到商家推荐系统中。在这种情况下,位置社交网络中的商家被看成是一个普通的物品接受用户点评。然而由于位置社交网络的特殊性,其具有传统推荐系统研究中不具备的多源异构信息,而这些信息可以帮助更好的学习到用户的偏好并有助于提高推荐的准确率,因此融合这些多源信息来进行商家推荐系统的设计值得研究。尽管之前的一些研究也在这些方面有一些进展,如在一个模型中融入相对较全面的多源异构信息来进行推荐,且模型具有一定的鲁棒性,即能够在部分信息缺失的情况下依然能够保证推荐系统的正常运行,现有的模型关于社交关系信息建模方面利用了社交网络所具有的天然社交关系进行商家推荐。然而,最近的社会学研究结果表明这种方法可能不是最恰当的。研究指出,将人们聚在一起的规则包括:(1)习惯或生活方式;(2)态度;(3)口味;(4)道德标准;(5)经济水平;(6)已经知道的人。显然,规则3和规则6是现有推荐系统考虑的主流因素,但利用社交网络天然社交关系进行商家推荐存在的最大的问题在于,虽然用户彼此之间是好友,但彼此间生活方式差异可能会巨大,因此好友推荐的结果可能跟自己希望的截然不同,而规则1可能是最直观的,即利用相似生活方式的社交关系进行商家推荐则可能更为精准。
技术实现要素:
为了帮助更好地学习到用户的偏好,并有助于提高推荐的准确率,本发明提供一个融合用户的点评文本,社交关系以及用户访问位置的地理位置信息的联合模型的优化方案。
为此目的,本发明采用的技术方案是一种基于位置社交网络的商家推荐的优化方法,具体包括如下步骤:
步骤1、构建原多源信息融合模型cosolorec,包含内容,社交和位置信息;
步骤2、基于生活方式相似的社交关系信息进行建模,即在cosolorec中社交关系信息建模阶段,采用基于用户的协同过滤的方法来预测商家对用户的吸引力,通过lda算法引入带有生活方式属性的内容计算用户间的相似度;
步骤3、采用余弦相似度进行度量;
步骤4、采用改进的杰卡德相关系数进行度量。
进一步,上述步骤1中的原多源信息融合模型包含个人兴趣和距离,用下式来表示:
probability=(pex+pim)×((1-λ)pl+λpf)
其中pim表示隐式兴趣概率,pex表示显示兴趣概率,pl和pf分别表示地理上距离影响概率和基于好友心理上的影响概率,λ是用来调整地理距离与心理距离在贡献概率中的比重大小。
上述步骤2中,所述计算用户间的相似度的具体步骤如下:
(1)将用户的日常生活与文档主题生成模型进行类比,即将用户的日常生活模拟为文档,将生活方式作为主题,将活动作为词;
(2)采用概率主题模型来从“生活文档”中发现用户隐藏的“生活方式向量”;
(3)用户间生活方式的相似度定义为用户间整体生活方式向量的相似度与主要生活方式向量相似度相乘的形式。
上述步骤3中所述的整体生活方式向量的生成具体包括:将用户的日常生活与文档主题生成模型进行类比,即将用户的日常生活模拟为文档,将生活方式作为主题,将活动作为词,采用概率主题模型来从“生活文档”中发现用户隐藏的“生活方式向量”,具体如下:
令w=[w1,w2....ww]表示一组活动,其中wi是第i个活动,w是活动的总数,令z=[z1,z2....zz]表示一组生活方式,其中zi是第i种生活方式,z是生活方式的总数,令d=[d1,d2....dn]表示一组生活文档,其中di是第i个生活文档,n是用户总数,p(wi|dk)表示在生活文档dk中出现活动wi的概率,p(wi|zj)表示在生活方式zj中出现活动wi的概率,p(zj|dk)表示在生活文档中dk中出现生活方式zj的概率,根据概率主题模型,则有:
p(wi|dk)可以通过使用生活文档dk的“活动袋”模型容易地得到,计算:
fk(wi)表示活动wi在生活文档dk中出现的频次,将给定的所有用户的生活文档进行矩阵分解为:p(w|d)=p(w|z)p(z|d)
p(w|d)=[p(w|d1),p(w|d2),...p(w|dn)]是活动-生活文档矩阵,其包含在每个生活文档上每个活动出现的概率,p(w|dk)=[p(w1|dk),p(w2|dk),...p(ww|dk)]t是活动-生活文档矩阵中的第k列,表示用户k的生活文档dk上各个活动出现的概率,
p(w|z)=[p(w|z1),p(w|z2),...p(w|zz)]是活动-生活方式矩阵,表示在每个生活方式上每个活动出现的概率,p(w|zk)=[p(w1|zk),p(w2|zk),...p(ww|zk)]t是活动-生活方式矩阵中的第k列,表示用户k的生活方式zk上各个活动出现的概率。
p(z|dk)=[p(z1|dk),p(z2|dk),...p(zz|dk)]t是生活方式-生活文档矩阵,其包含每个生活方式在每个生活文档上出现的概率,据此获得所有用户的生活方式向量:
li=[p(z1|di),p(z2|di),...p(zz|di)]和li′=[p(z1|di′),p(z2|di′),...p(zz|di′)]分别表示用户i和用户i′的生活方式向量。
上述步骤3中所述主要生活方式向量的生成具体包括:
首先定义一组用户的主要生活方式集,即定义用户i的主要生活方式的集合di是满足以下要求的所有生活方式的子集:
1)集合的总概率分布大于或等于预定义的阈值λ;
2)集合中任何生活方式的概率分布大于或等于不在集合中的任何生活方式的概率分布;
3)集合应该具有最小数量的生活方式;
然后按照生活方式的概率以降序排列得到生活方式向量
最后,可以得到用户i的主要生活方式向量di={zi1,...,ziqi}。
上述相似度的计算过程如下:
用户i和用户i′之间的生活方式的相似性,表示为sim(i,i′),定义如下:
sim(i,i′)=simc(i,i′)·simd(i,i′)
其中simc(i,i′)用于测量用户间整体的生活方式向量的相似度,simd(i,i′)用于测量用户间主要生活方式向量的相似度。
上述采用余弦相似度进行度量具体包括:采用常用的余弦相似度表示simc(i,i′),即simc(i,i′)=cosθ,θ表示的是用户i生活方式向量li和用户i′生活方式向量li′间的夹角。
上述采用改进的杰卡德相关系数进行度量具体包括:在杰卡德相关系数上做了改进,定义如下:
simd(i,i′)的范围是[0,1],观察到相同生活方式的百分比越高,相似性越大,
当di和di′之间没有重叠时,相似度为0;当di和di′相同时,相似度为1,simc(i,i′)和simd(i,i′)在0和1之间变化。
与现有技术相比,本发明的有益效果在于:
1,本发明在原联合模型中利用社交关系信息建模的基础上,提出了一种基于相似生活方式的好友推荐方法,定义了一个新的带有生活方式属性的相似度来测量两个用户生活方式之间的相似性。
2,本发明通过引入了额外的信息源,使得新相似度的计算更为准确,从而缓解原相似度中所带来的数据稀疏问题,提高了系统推荐准确率。
附图说明
图1为cosolorec多源信息融合建模的推荐系统框架图。
图2为aggregatedlda图模型。
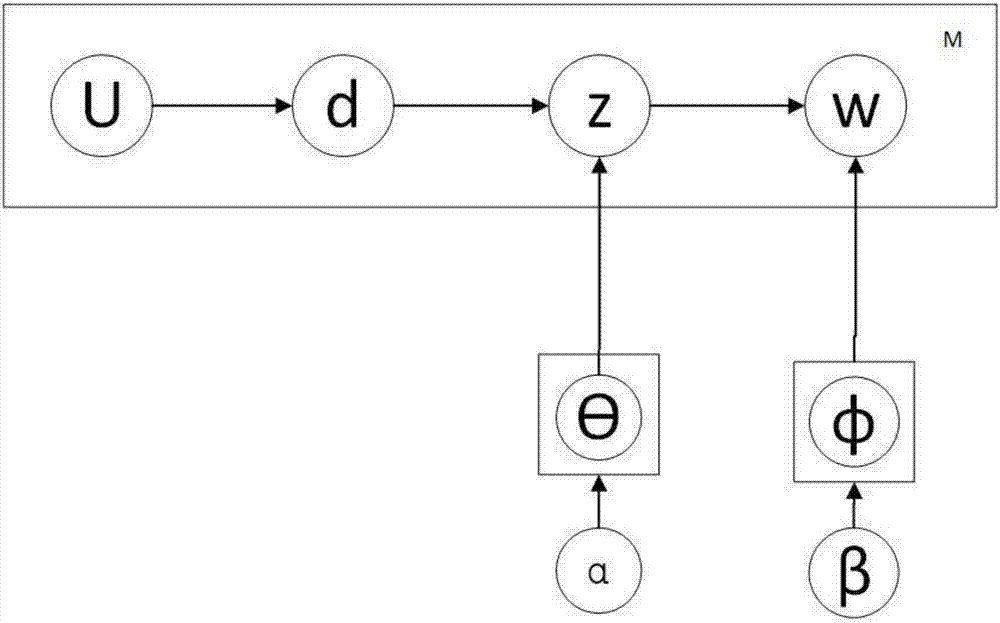
图3为cosolorec概率图模型。
具体实施方式
以下结合说明书附图,对本发明创造作详细说明。
本发明涉及杰卡德相关系数模型,文档主题生成模型等,在原多源信息融合模型中利用社交关系信息建模阶段,提出了一种基于相似生活方式的好友推荐方法,对用户访问商家行为进行建模,预测用户偏好,从而为用户个性化地推荐商家。本发明使用基于相似生活方式的好友关系的协同过滤(collaborativefiltering,cf)对社交关系建模,将用户的日常生活模型模拟为文本挖掘中的文档模型,再通过(latentdirichletallocation)lda算法提取出用户的生活方式向量。
生活方式信息通常无法直接被提取出来,但其与日常生活和活动密切相关。受文本挖掘领域最新研究的启发,将用户的日常生活模型模拟为文本挖掘中的文档模型。文档模型认为一篇文章的每个词语都是通过一定概率选择了某个主题,并从这个主题中以一定概率选择某个词语,若给定所有的文档,即将文档-词矩阵分解成文档-主题矩阵与主题-词矩阵,对应到日常生活模型,即将生活文档-活动矩阵分解成生活文档-生活方式矩阵与生活方式-活动矩阵,再通过lda算法提取出用户的生活方式向量。
如图1、图2及图3所示,本发明在一个融合了用户的点评文本,社交关系以及用户访问位置的地理位置信息的联合模型基础上进行了改进,即在利用社交关系信息建模阶段,基于相似生活方式的好友推荐方法,定义了一个新的带有生活方式属性的相似度来测量两个用户生活方式之间的相似性。该方法包括如下步骤:
步骤1、原多源信息融合模型
基于图1的框架提出联合模型cosolorec(涉及了内容(content),社交(social)和位置(location),因而称其推荐算法为cosolorec)。该模型结合了地理信息,社会关系以及文本等多源异构信息。模型由四大部分构成,且认为影响一个用户光顾商家概率的因素大致有两点,一个是个人兴趣,二是距离。每个方面又可以拆分成各两个小方面。
对于个人兴趣来说,可以分为显式的兴趣和隐式的兴趣。显式的兴趣可以通过从用户的点评文本中挖掘得到。具体的采用了隐狄利克雷分布来抽取用户和商家的主题分布,并通过匹配两者来判别用户对商家是否感兴趣。显式兴趣之所以称之为显式兴趣,是因为通过主题模型抽取出来的主题有明确的意义和解释。相较于显式兴趣,隐式兴趣顾名思义则是兴趣不可解释,这是由于除去用户显式表露出来的兴趣之外,还有很多因素影响着用户对商户的兴趣,例如心情,天气以及突发状况等。使用概率隐变量模型来对用户的隐式兴趣建模。具体来说,假设用户和商家的隐藏兴趣由少量的特征来决定,通过用户特征矩阵和商家特征矩阵的学习可以得到用户和商家的兴趣匹配程度,因而得到在隐藏兴趣方面用户对商户的感兴趣程度(即概率)。对于距离来说,主要分为物理上的距离和心理上的距离。物理上的距离,通过对球形地理空间上用户光顾商家的行为进行建模可以获得用户在该空间上光顾该商家的概率。心理上的距离由社交网络中基于相似生活方式的趋同性理论所保证,表明了用户在心理上对某一商家的认可程度。用户对商家的喜好受生活方式相似的好友的影响并与之相近似,因而可以使用生活方式相似的好友对商家的喜好概率来建模用户对商家心理上的距离的概率。最后通过以下模型来将这几者信息融合起来,如下所示:
probability=(pex+pim)×((1-λ)pl+λpf)
其中pim表示隐式(implicit)兴趣概率,pex表示显示(explicit)兴趣概率,pl和pf分别表示地理上(location)距离影响概率和基于相似生活方式的好友(friend)心理上的影响概率。
lda模型是目前应用最广泛的一种概率主题模型,该模型认为文档是若干主题的混合分布,而每个主题又是一个关于单词的概率分布,它具有比其他模型更全面的文本生成假设,常被用于计算论文的主题向量及基于内容的推荐方法。有两种表示方法,分别为生成模型表示法和图模型表示法。生成模型适用于仅生成一篇文档,图模型适用于生成m份包含n个单词的文档。
图2即采用的是lda图模型表示法,是一种将概率和传统的图结构结合起来的表示方法。通过图结构的清晰表示,可以更好地理解概率的分布,具体过程如下:
(1)对文本集中的任意文本d,其单词集合为nd;
(2)计算该文本d的文本-主题特征向量θ,其中θ是参数为给定正数α的多项分布函数,再从参数为θ的多项分布函数中随机采样得到一个主题z;
(3)计算主题z的主题-单词特征向量φ,φ是参数为给定正数β的多项分布函数,再从参数为φ的多项分布函数中随机采样得到一个单词w,且w属于nd。
为了给用户推荐其感兴趣的商家,因而需要预测用户在所有候选商家上的兴趣偏好。用户对商家的兴趣偏好高,即表明用户有更大的可能性会光顾该商家,因而也就更应该将商家推荐给该用户。用户对商家的光顾可能性在数学上表示为用户对商家的光顾概率。用户对商家的光顾概率受用户的兴趣与用户与商家的距离两者调控。当兴趣越大,则光顾概率越高,而当距离越近,则光顾概率也相应的越高。
用户对商家的光顾概率与由距离决定的光顾概率成正比。于是有以下形式:
p(i,j)∝η(i,j)((1-λ)pl(i,j)+λpf(i,j))(1)
其中η(i,j)表示的是用户i对商家j的兴趣大小,pl(i,j)表示的是受地理位置影响的用户i对商家j的光顾概率,pf(i,j)表示的是受基于相似生活方式的好友关系影响的用户i对商家j的光顾概率,λ是用来调整地理距离与心理距离在贡献概率中的比重大小。特别的,当λ为1的时候,仅有心理距离作用,这个时候无需对地理距离进行建模。当λ为0的时候,仅有物理距离作用,这个时候无需对心理距离进行建模。由此可见,该模型从某种程度上来说,对于特殊情况下,信息缺失的情况具有很好的鲁棒性。由于兴趣包含了显式兴趣与隐式兴趣两个方面,因而兴趣η(i,j)又有两个部分构成,一为基于概率主题模型的显式兴趣
由此,完整的联合模型过程如下:
1.drawauserinterest
(a)generatoruserlatentfactoruiw~gamma(αu,βu)
(b)generatoritemlatentfactorvjw~gamma(αv,βv)
y(i,j)~p(p(i,j))(2)
2.
其中θi表示的是用户的兴趣主题分布,πj表示的是商家表现在用户感兴趣的主题上的分布。ui表示的是用户的特征向量,vj表示的是商家的特征向量,αu、βu、αv、βv均为超参,uiw与vjw表示的是用户的兴趣和商家的表现的分布。该过程对应的概率图模型如图3所示。
步骤2、基于生活方式相似的社交关系信息建模
社交网络信息中的社交关系指的是用户与用户建立的或者单向或者双向的好友连接关系。在社交网络中,根据“趋同性”理论,用户倾向与自己有相同兴趣爱好的好友建立联系,即用户与自己的好友有相似的兴趣爱好。利用社交网络的该特性,可以对用户心理上对商家的距离进行度量。将用户i的所有对商家j评分过的好友作为用户i的好友集合,采用基于用户的协同过滤的方法来预测商家对用户的吸引度,其公式如下:
rf(i,j)指的是用户i对商家j的预测评分,
由于概率在【0,1】区间内,故将预测评分归一化,如下:
其中pf(i,j)表示的是预测用户i光顾商家j的概率,rmax是所有评分中的最大值,fi指的是用户i的所有对商家j评分过的好友集合,ri′j指的是用户i′对光顾过的商家j的评分,
因此本发明在原多源信息融合模型中利用社交关系信息建模的基础上,提出了一种基于相似生活方式的好友推荐方法,定义了一个新的带有生活方式属性的相似度来测量两个用户生活方式之间的相似性,具体如下:
令w=[w1,w2,…,ww]表示一组活动,其中wi是第i个活动,w是活动的总数。令z=[z1,z2,…,zz]表示一组生活方式,其中zi是第i种生活方式,z是生活方式的总数。令d=[d1,d2,…,dn]表示一组生活文档,其中di是第i个生活文档,n是用户总数。p(wi|dk)表示在生活文档dk中出现活动wi的概率,p(wi|zj)表示在生活方式zj中出现活动wi的概率,p(zj|dk)表示在生活文档dk中出现生活方式zj的概率。根据概率主题模型,则有:
p(wi|dk)可以通过使用生活文档dk的“活动袋”模型(对应文本挖掘中的词袋模型)容易地得到计算:
fk(wi)表示活动wi在生活文档dk中出现的频次
lk=[p(z1|dk),p(z2|dk)....p(zz|dk)]表示用户k的生活方式向量,代表该用户的生活方式。目标是根据给定的所有用户的生活文档发现每个用户的生活方式向量。在等式(6)中虽然可以很容易计算p(wi|dk),但是由于生活方式的隐藏特征,p(wi|zj)跟p(zj|dk)难以解决。因此需使用如下lda分解算法来求解方程,从而获得用户的生活方式向量。给定所有用户的生活文档,公式(6)可以进一步表示为矩阵分解问题:
p(w|d)=p(w|z)p(z|d)(8)
p(w|d)=[p(w|d1),p(w|d2),...p(w|dn)]是活动-生活文档矩阵,其包含在每个生活文档上每个活动出现的概率,p(w|dk)=[p(w1|dk),p(w2|dk),...p(ww|dk)]t是活动-生活文档矩阵中的第k列,表示用户k的生活文档dk上各个活动出现的概率。
p(w|z)=[p(w|z1),p(w|z2),...p(w|zz)]是活动-生活方式矩阵,表示在每个生活方式上每个活动出现的概率,p(w|zk)=[p(w1|zk),p(w2|zk),...p(ww|zk)]t是活动-生活方式矩阵中的第k列,表示用户k的生活方式zk上各个活动出现的概率。
p(z|d)=[p(z|d1),p(z|d2),...p(z|dn)]是生活方式-生活文档矩阵,其包含在每个生活文档上每个生活方式出现的概率。
p(z|dk)=[p(z1|dk),p(z2|dk),...p(zz|dk)]t是主题文档矩阵中的第k列,其表示用户k的生活方式在生活文档dk上的概率。
li=[p(z1|di),p(z2|di),...p(zz|di)]和li′=[p(z1|di′),p(z2|di′),...p(zz|di′)]分别表示用户i和用户i′的生活方式向量。
由于相似性不仅受他们整体的生活方式向量影响,而且也受最重要的生活方式向量(也称为主要生活方式)影响,即受矢量内具有较大概率值的元素影响。本发明还认为,如果他们的大多数生活方式完全不同,两个用户不会有很多相似性。因此,用户i和用户i′之间的生活方式的相似性,表示为sim(i,i′),定义如下:
其中simc(i,i′)用于测量用户间整体的生活方式向量的相似度,simd(i,i′)用于测量用户间主要生活方式向量的相似度。
采用常用的余弦相似性度量表示simc(i,i′),即simc(i,i′)=cosθ,θ表示的是用户i生活方式向量li和用户i′生活方式向量li′之间的夹角。(10)
为了计算等式(9)中的simd(i,i′),首先定义一组用户的主要生活方式集。
定义:用户i的主要生活方式的集合di是满足以下要求的所有生活方式的子集:
1)集合的总概率分布大于或等于预定义的阈值λ。
2)集合中任何生活方式的概率分布大于或等于不在集合中的任何生活方式的概率分布。
3)集合应该具有最小数量的生活方式。
这些要求保证具有较大概率值的生活方式更可能被包括在集合中。为了找到di,按照生活方式的概率以降序排列得到生活方式向量
最后,可以得到主要生活方式集
杰卡德相关系数最初被用来衡量两个集合之间的相似程度,被定义为集合的交集大小与集合的并集大小的比值,其更加适合于离散维度特征的向量之间的相似度,如下:
本发明的相似性度量simd(i,i′)用于测量两个用户的主要生活方式集的相似性,在杰卡德相关系数上做了改进,定义如下:
simd(i,i′)的范围是[0,1],观察到相同生活方式的百分比越高,相似性越大。
当di和di′之间没有重叠时,相似度为0;当di和di′相同时,相似度为1。simc(i,i′)和simd(i,i′)在0和1之间变化,得出结论:相似性度量sim(i,i′)在0和1之间变化。
- 还没有人留言评论。精彩留言会获得点赞!