本发明涉及机器人仿真技术领域,具体涉及一种基于kinect的darwin机器人关节映射解析方法。
背景技术:
仿人机器人是机器人领域的重要研究方向之一,体态感知作为一种自然的人机交互形式,在交互过程中能够很好的识别与传递人的意图,并携带有极为丰富的信息量。当前机器人技术的研究正朝着智能化和多样化的方向发展,为符合各种复杂、恶劣环境的特殊要求,需要机器人具有更高的适应性以及具备一定的学习能力,需要机器人能自主移动到指定的地方,在工业、医疗、航空、国防领域及危险场合等进行工作。而传统机器人往往只针对特定的任务,且需要大量人为编程,费时费力,难以满足灵活性的要求。为此人们正在积极探索机器人模仿学习的行为控制,将开发人员从复杂的编程工作中解放出来。由于人体关节自由度和仿人机器人的自由度不同,以及仿人机器人的物理约束等问题,限制了仿人机器人直接模仿人体行为。而目前大部分的研究工作主要集中在上半身的动作模仿,采用的关节解析方法也主要针对上半身,目前亟待提出一种关节解析方法能实现将人体关节信息映射到darwin机器人上,以解决机器人自由度约束等情况的影响,并能保证在模仿过程中机器人全身的重心稳定。
技术实现要素:
本发明的目的是为了解决现有技术中的上述缺陷,提供一种基于kinect的darwin机器人关节映射解析方法,该解析方法首先利用kinect采集到的人体关节骨骼数据,然后将kinect人体关节骨骼数据通过关节解析后映射到darwin机器人的关节,并使其在最大程度上实现了darwin机器人模仿人体动作。
本发明的目的可以通过采取如下技术方案达到:
一种基于kinect的darwin机器人关节映射解析方法,所述方法包括下列步骤:
s1、利用kinect采集人体关节点p的骨骼数据;
s2、建立基于人体的参考坐标系,并将人体关节点p的骨骼数据映射到该坐标系上,通过同一骨架的两个关节点可以得到darwin机器人的单位关节矢量v;
s3、通过欧拉旋转分析,将关节矢量v解析得到kinect与darwin机器人共同关节的相应转动角度θ;
s4、对darwin机器人脚部扩展关节进行重心稳定分析,得到darwin机器人单、双脚稳定站立的脚关节角度,对舵机的转动角度θ进行计算和校准。
进一步地,所述人体关节点p的骨骼数据包括:头部、颈部、躯干、左肩、左肘、左手、右肩、右肘、右手、左臀、左膝、左脚、右臀、右膝、右脚,用p1-p15表示;
所述单位关节矢量v包括:头部矢量、颈部矢量、左上臂矢量、左下臂矢量、右上臂矢量、右下臂矢量、左大腿矢量、左小腿矢量、右大腿矢量、右小腿矢量,用v1-v10表示。
进一步地,定义机器人初始状态为人体的站立姿态,则所有关节矢量的初始坐标可表示[0-10]t,根据欧拉旋转关系可以得到变换阵re,可以得到关节矢量v=re[0-10]t,其中re与旋转顺序、次数和旋转轴有关,有一到多个旋转算子组成,旋转算子rx(θ)、ry(θ)、rz(θ)分别表示绕坐标系x、y、z轴旋转θ角的变换阵,有:
θ角的id号为i的舵机转过的对应角度为θi,第i个关节矢量vi的各轴分量分别表示为vxi、vyi、vzi;
darwin机器人头部有2个舵机,id为19和20,id19舵机级联id20舵机,id19控制y转向,id20控制x转向;
darwin机器人左右手各有3个舵机,id为1-6,其中,关于右手,id1舵机级联id3舵机,再级联id5舵机,id1控制右手x转向,id3控制右手y转向,id5控制右手z转向,关于左手,id2舵机级联id4舵机,再级联id6舵机,id2控制左手x转向,id4控制左手y转向,id6控制左手z转向;
darwin机器人左右脚各有6个舵机,id为7-18,关于右脚,id7舵机级联id9舵机,再级联id11舵机,再级联id13舵机,再级联id15舵机,再级联id17舵机,id7控制右脚y转向,id9控制右脚z转向,id11控制右脚x转向,id13控制右脚x转向,id15控制右脚x转向,id17控制右脚z转向;关于左脚,id8舵机级联id10舵机,再级联id12舵机,再级联id14舵机,再级联id16舵机,再级联id18舵机,id8控制左脚y转向,id10控制左脚z转向,id12控制左脚x转向,id14控制左脚x转向,id16控制左脚x转向,id18控制左脚z转向。
进一步地,θ1、θ2的取值范围(-ππ),其他角度取值范围另外,θ3、θ5、θ6、θ9、θ10只能取正,θ4、θ13、θ14、θ20只能取负。
进一步地,所述步骤s4具体过程如下:
定义
r1=rx(θ1),r2=rx(θ2),r3=r1rz(θ3),r4=r2rx(θ4),
r5=r3rz(θ5),r6=r4rx(θ6),
r7=ry(θ7),r8=ry(θ8),r9=r7rz(θ9),r10=r8rz(θ10),
r11=r9rx(θ11),r12=r10rx(θ12),
r13=r11rx(θ13),r14=r12rx(θ14),r15=r13rx(θ15),r16=r14rx(θ16),
r17=r15ry(θ17),r18=r16ry(θ18),r19=ry(θ19),r20=r19rx(θ20)
po1=poff1,po2=poff2,po3=po1+r1poff3,po4=po2+r2poff4,
po5=po3+r3poff5,po6=po4+r4poff6,po7=poff7,po8=poff8,
po9=po7+r7poff9,po10=po8+r8poff10,po11=po9+r9poff11,po12=po10+r10poff12,
po13=po11+r11poff13,po14=po12+r12poff14,po15=po13+r13poff15,po16=po14+r14poff16,po17=po15+r15poff17,po18=po16+r16poff18,po19=poff19,po20=po19+r19poff20
右手重心位置:
左手重心位置:
右脚重心位置:
左脚重心位置:
头部重心位置:
整体重心位置:
同上,可计算右脚平面和左脚平面中心点坐标分别为:
pa=po17+r17[10-33.50]t,pb=po18+r18[-10-33.50]t
根据双足站立稳定条件可以得到脚平面法向量:
此时拓展关节矢量v10=v11=f,则机器人能够稳定站立,由旋转关系有:v10=rx(θ15)rz(θ17)v7,v11=rx(θ16)rz(θ18)v9,可得结果:
若机器人为双脚站立,如果重心g投影点c不在两脚平面中心点连线上,则机器人将左右不平衡,需要修正θ9、θ10,修正方法为加入偏移量±通过递归方法直到找到稳定点;
若机器人为单脚站立,则重心投影应落在该脚平面的中心点上,此时机器人能稳定站立,以右脚站立时,有:f=pb-pg,解析过程相同,以左脚站立时,有f=pb-pg。
进一步地,所述舵机的转动角度θ的解析关系如下:
θ1=atan2(sinθ5vy3-cosθ3cosθ5vz3,-sinθ5vz3-cosθ3cosθ5vy3),
θ2=atan2(sinθ6vy5-cosθ4cosθ6vz5,-sinθ6vz5-cosθ4cosθ6vy5),
θ3=arcsin(vx2),
θ4=arcsin(vx4),
θ5=arccos(v2·v3),
θ6=arccos(v4·v5),
θ7=0,
θ8=0,
θ11=-arcsin(vz6),
θ12=-arcsin(vz8),
θ13=-arccos(v6·v7),
θ14=-arccos(v8·v9),
θ20=-arccos(vy1)。
本发明相对于现有技术具有如下的优点及效果:
采用统一的欧拉旋转分析方法进行解算,其欧拉旋转顺序与达尔文机器人的关节级联顺序相同,直观易于理解,其解析角度与达尔文机器人舵机角度基本相同,相较于传统的矢量计算方法,采用统一参考坐标系的欧拉角度计算方法思路更加清晰,拓展性更强,方便重心位置与末端位置的计算,该方法适用于头部、手部和脚部的关节解析,适用性强。该方案还采用重心稳定分析的方法对机器人双足站立进行了分析,能够保证机器人的稳定站立,实现全身的基本模仿。同时,在能判别单脚站立的情况下,该重心稳定方法也同样适用于单脚站立情况。
附图说明
图1是kinect人体关节点信息图;
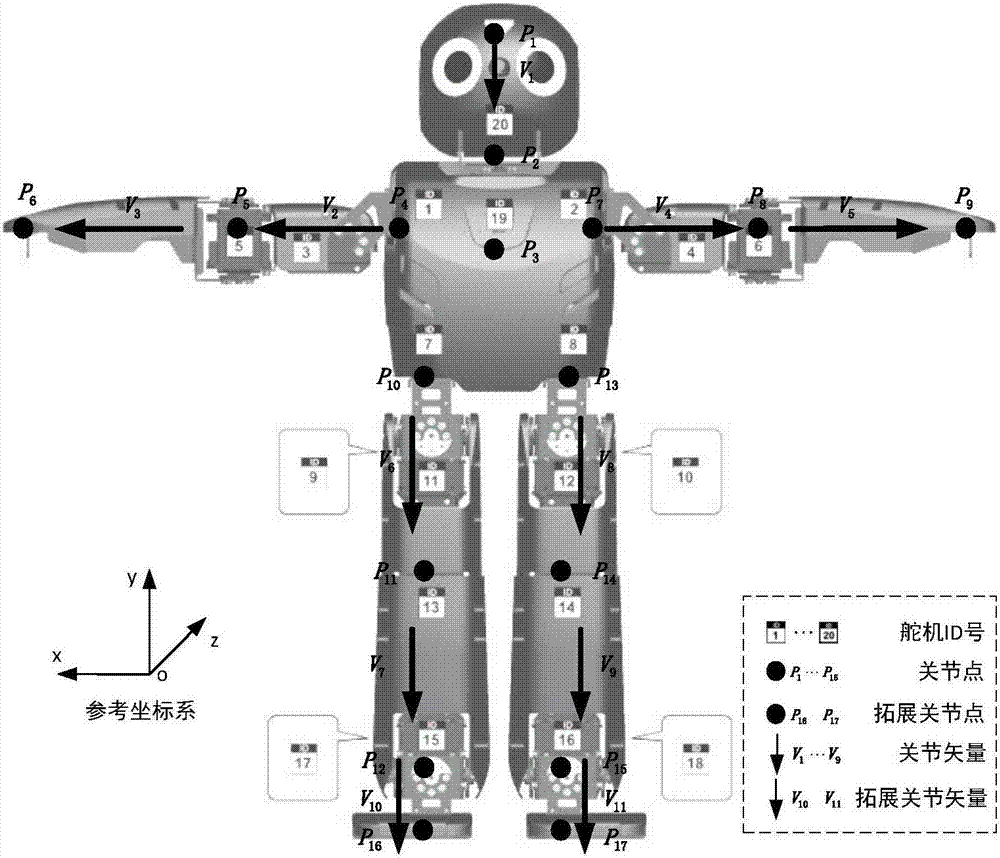
图2是darwin机器人的关节矢量图;
图3是kinect到darwin机器人的关节映射解析方法流程图。
具体实施方式
为使本发明实施例的目的、技术方案和优点更加清楚,下面将结合本发明实施例中的附图,对本发明实施例中的技术方案进行清楚、完整地描述,显然,所描述的实施例是本发明一部分实施例,而不是全部的实施例。基于本发明中的实施例,本领域普通技术人员在没有作出创造性劳动前提下所获得的所有其他实施例,都属于本发明保护的范围。
实施例
本实施例公开了一种基于kinect的darwin机器人关节映射解析方法,该解析方法首先利用kinect采集人体关节骨骼数据,然后将kinect人体关节骨骼数据通过关节解析后映射到darwin机器人的关节,并使其在最大程度上实现了darwin机器人模仿人体动作。该方法具体包括下列步骤:
s1、利用kinect采集人体关节点p的骨骼数据;
该步骤中利用openni能够读取到kinect的24个关节点信息,分别为:头部、颈部、躯干、腰、左领、左肩、左肘、左腕、左手、左指尖、右领、右肩、右肘、右腕、右手、右指尖、左臀、左膝、左踝、左脚、右臀、右膝、右踝、右脚,在实际应用中只有15个关节点数据有效,分别为:头部、颈部、躯干、左肩、左肘、左手、右肩、右肘、右手、左臀、左膝、左脚、右臀、右膝、右脚,用p1-p15表示。由于kinect的深度图与彩色图配准的精度问题,对关节点数据进行初步补偿,并采用滑动均值滤波减缓关节点数据波动程度。
s2、建立基于人体的参考坐标系,并将人体关节点p的骨骼数据映射到该坐标系上,通过同一骨架的两个关节点可以得到darwin机器人的单位关节矢量v,分别为:头部矢量、颈部矢量、左上臂矢量、左下臂矢量、右上臂矢量、右下臂矢量、左大腿矢量、左小腿矢量、右大腿矢量、右小腿矢量,用v1-v10表示。
以关节点躯干为坐标系原点,规定关节点左肩指向关节点右肩的方向为参考坐标系的x方向,关节点左肩、右肩与躯干平面法向量指向人体背面的方向为z方向,则根据右手坐标系规则可确定y方向。可以得到坐标系变换阵以头部矢量为例,其相关的两个关节点为关节点头部与颈部,则其他矢量计算相同。
s3、通过欧拉旋转分析,将关节矢量v解析得到kinect与darwin机器人共同关节的相应转动角度θ;
定义机器人初始状态为人体的站立姿态,则所有关节矢量的初始坐标可表示[0-10]t,根据欧拉旋转关系可以得到变换阵re,可以得到关节矢量v=re[0-10]t,其中re与旋转顺序、次数和旋转轴有关,有一到多个旋转算子组成,旋转算子rx(θ)、ry(θ)、rz(θ)分别表示绕坐标系x、y、z轴旋转θ角的变换阵,有:
θ角的取值范围为(-ππ),为表示方便,id号为i的舵机转过的对应角度为θi,第i个关节矢量vi的各轴分量分别表示为vxi、vyi、vzi。由于机器人机械限制,θ1、θ2可取(-ππ),其他角度只能取另外,θ3、θ5、θ6、θ9、θ10只能取正,θ4、θ13、θ14、θ20只能取负。
1)darwin机器人头部有2个舵机,id为19和20,id19舵机级联id20舵机,id19控制y转向,id20控制x转向,则头部矢量v1=ry(θ19)rx(θ20)[0-10]t,可以得到
2)darwin机器人左右手各有3个舵机,id为1-6,以右手为例,id1舵机级联id3舵机,再级联id5舵机,id1控制右手x转向,id3控制右手y转向,id5控制z转向,则右上臂矢量v2=rx(θ1)ry(θ3)[0-10]t,可以得到θ3=arcsin(vx2),则右下臂矢量v3=rx(θ1)ry(θ3)rx(θ5)[0-10]t,可以得到考虑到θ1取值范围为(-ππ),修改为θ1=atan2(sinθ5vy3-cosθ3cosθ5vz3,-sinθ5vz3-cosθ3cosθ5vy3)。而θ5为v2和v3的夹角,所以θ5=arccos(v2·v3)。左手情况相同。
3)darwin机器人左右脚各有6个舵机,id为7-18,以右脚为例,id7舵机级联id9舵机,再级联id11舵机,再级联id13舵机,再级联id15舵机,再级联id17舵机,id7控制y转向,id9控制z转向,id11控制x转向,id13控制x转向,id15控制x转向,id17控制z转向。为降低解析复杂度和消除多解情况,忽略id7舵机的控制,则右大腿矢量v6=rz(θ9)rx(θ11)[0-10]t,可以得到θ11=-arcsin(vz6),而θ13为v6和v7的夹角,所以θ13=-arccos(v6·v7)。左脚情况相同。
s4、通过重心稳定分析,对舵机的转动角度θ进行计算和校准。
以上能实现机器人的动作模仿,但机器人不能稳定站立,通过扩展两个关节矢量,通过重心稳定方法控制脚踝部分的4个舵机,可以实现机器人的稳定站立。先不考虑地面不水平和单脚站立情况,为了实现机器人双脚稳定站立,则需要满足条件:机器人的两个脚平面与地面完全贴合;机器人的重心投影落在两脚平面中心点连线上。通过查阅资料与计算测量,可得到机器人各部件的重心信息,如表1所示。其中,重心位置为该关节重心距离旋转中心的距离,偏移位置为旋转中心距离上一个关节旋转中心的位置。
表1.darwin机器人各部件重心信息表
根据空间坐标平移与旋转变换,可得到机器人整体的重心位置。定义
r1=rx(θ1),r2=rx(θ2),r3=r1rz(θ3),r4=r2rx(θ4),
r5=r3rz(θ5),r6=r4rx(θ6),
r7=ry(θ7),r8=ry(θ8),r9=r7rz(θ9),r10=r8rz(θ10),
r11=r9rx(θ11),r12=r10rx(θ12),
r13=r11rx(θ13),r14=r12rx(θ14),r15=r13rx(θ15),r16=r14rx(θ16),
r17=r15ry(θ17),r18=r16ry(θ18),r19=ry(θ19),r20=r19rx(θ20)
po1=poff1,po2=poff2,po3=po1+r1poff3,po4=po2+r2poff4,
po5=po3+r3poff5,po6=po4+r4poff6,po7=poff7,po8=poff8,
po9=po7+r7poff9,po10=po8+r8poff10,po11=po9+r9poff11,po12=po10+r10poff12,
po13=po11+r11poff13,po14=po12+r12poff14,po15=po13+r13poff15,po16=po14+r14poff16,po17=po15+r15poff17,po18=po16+r16poff18,po19=poff19,po20=po19+r19poff20
右手重心位置:
左手重心位置:
右脚重心位置:
左脚重心位置:
头部重心位置:
整体重心位置:
同上,可计算右脚平面和左脚平面中心点坐标分别为:
pa=po17+r17[10-33.50]t,pb=po18+r18[-10-33.50]t
根据双足站立稳定条件可以得到脚平面法向量:
此时拓展关节矢量v10=v11=f,则机器人能够稳定站立,由旋转关系有:v10=rx(θ15)rz(θ17)v7,v11=rx(θ16)rz(θ18)v9,可得结果:
若重心g投影点c不在两脚平面中心点连线上,则机器人将左右不平衡,需要修正θ9、θ10,修正方法为加入偏移量±通过递归方法直到找到稳定点。
若机器人为单脚站立,则重心投影应落在该脚平面的中心点上,此时机器人能稳定站立,以右脚站立为例,有:f=pb-pg,解析过程相同。以左脚站立为例,有f=pb-pg。
综上,可得到关节解析表,如下:
表2.关节解析表
综上所述,本发明公开的一种基于kinect的darwin机器人关节映射解析方法,利用kinect获取人体的15个关节点,通过补偿与后,在参考坐标系中构建9个单位关节矢量,并根据darwin机器人关节级联方式进行欧拉旋转分析,得到相应关节的角度,最后利用重心稳定分析对darwin机器人的脚部扩展关节进行解析,从而实现kinect到darwin机器人的动作模仿。
上述实施例为本发明较佳的实施方式,但本发明的实施方式并不受上述实施例的限制,其他的任何未背离本发明的精神实质与原理下所作的改变、修饰、替代、组合、简化,均应为等效的置换方式,都包含在本发明的保护范围之内。