适应性多尺度相关量化计算方法与流程

本发明涉及气象水文学研究领域，防灾减灾及灾害预警应用技术，具体为一种适应性多尺度相关量化计算方法。

背景技术：

变量相关性分析技术是气象水文学归因理论研究中的关键技术，是研究各气象水文过程、现象成因与机理的关键，对于从机理上探讨气象水文过程及现象具有重大理论与现实意义；在实践应用是，是开展防洪工程建设、水资源管理、防洪抗旱减灾等诸多生产实践的理论基础。

在时间序列分析中，两个变量相关性量化是传统的分析方法，同时也是变量相关性量化的最基础、最重要也是最主要的分析方法。主要以pearson相关分析为主。

传统的相关性量化法为：

上面有短线的变量为该变量的均值，x，y分别为两个变量，而rxy为x与y两个变量的相关系数。

现有的分析方法主要是线性相关，而且是全局相关，即没有考虑两变量在短历时上相关性的变化，在短历时上，两变量的相关是不稳性的，时而正相关，时而负相关，时而相关性不明显，即两变量在时域变化上存在非平稳性，因而，现有技术没有将时序变化的非平稳性考虑进去，从而易得出偏差性结果，给相关性量化分析结果增加了诸多不确定性，进而得出误导性结论。

技术实现要素：

本发明旨在克服现有技术的不足，提供一种新的适应性多尺度相关量化计算方法，基于变量时序变化过程中存在的非平稳性以及统计参数的不稳定性，本发明提出时序显微镜分析理论，从更小的时间尺度上研究两变量在不同时段的相关，克服了传统方法对时序非平稳性考虑的不足，避免了由时序非平稳性导致的分析结果的偏差甚至出现误导性结论。

本发明提供的一种适应性多尺度相关量化计算方法，该方法基于变量的时间序列，根据寻找突变点或变异点的方法将所述时间序列分段，再在每一小段区域内寻找突变点或变异点，直到没有突变点发现为止；再计算泛化相关指数，并验证其显著性，即完成变量相关性量化计算过程。

寻找突变点或变异点的方法为：

从时间序列自左向右滑动，计算时间序列每个点左右的偏差合并，如果某点的两篇偏差合并值越大，表示两端时间序列的趋势变化不一致，从而确定出该点是时间序列的变异点。

寻找突变点或变异点的具体过程为：

对每个变异点计算t检验统计量为：

再利用下式进行检验：

式中，sd表示某点的偏差合并，μ、n和s分别表示样本序列的均值、样本量及标准差，而其下标l或r，则分别表示从左到右分别计算每个点左边部分和右边部分的样本集；

基于上述计算，找到假设突变点中的最大值，根据下式检验其显著性：

其中，e为样本长度，η＝4.19lne–11.54和δ＝0.40是根据蒙特卡洛拟合的经验公式和经验参数，当达到设定的置信度水平值时，即认为所述假设的突变点为统计意义上的突变点。

所述计算泛化相关指数，并验证其显著性的具体过程为：

在k阶，给定局部相关系数，对应相应的时间长度为则

相应的检验统计量为：

而

其中，m为样本长度表示k阶的综合相关系数，表示k阶第i段的相关系数。根据的定义，结合相应的检验统计量，所述显著性检验采用z检验方法，则为泛化适应性相关系数。

所述置信度水平为95％。

本发明采用以上技术方案与现有技术相比，具有以下技术效果：

本发明是基于局域化相关性量化指标基础上，进行不同时段偏差合并的计算总值，然后取对数得出泛化相关性量化指标，克服了传统方法对时序非平稳性考虑的不足，避免了由时序非平稳性导致的分析结果的偏差甚至出现误导性结论。

附图说明

以下将结合附图对本发明作进一步说明：

图1为某一水文观测站实际观测的流量与水位过程图；

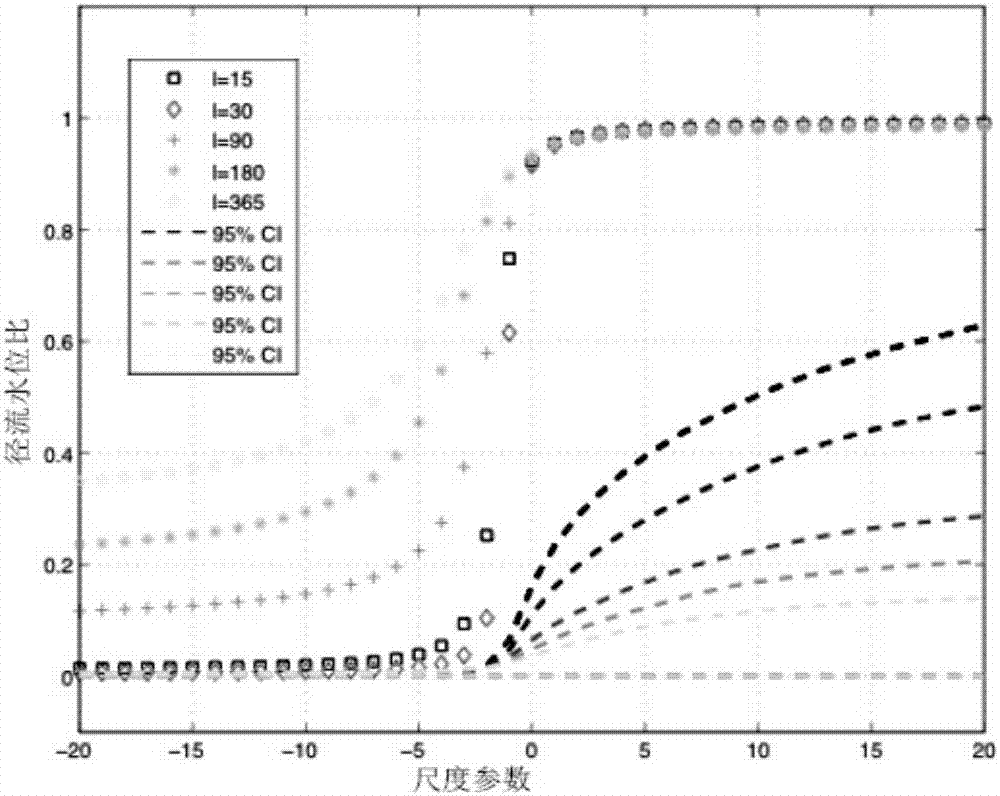
图2为采用本发明方法的局域化相关性量化指标。

具体实施方式

本发明的实施提供一种新的适应性多尺度相关量化计算方法，为使本领域技术人员更好地理解本发明的技术方案，下面结合附图和具体实施方式对本发明作进一步详细描述。通过参考附图描述的实施方式是示例性的，仅用于解释本发明，而不能解释为对本发明的限制。

传统的相关性量化法为：

上式中有短线的变量为该变量的均值，x，y分别为两个变量，而rxy为x与y两个变量的相关系数。而局域化相关量化指标的计算取决于对整个时间序列进行分段，而分段的依据则是寻找突变点或变异点。下面将找变异点步骤一一列出：

(1)假定某一点为变异点，然后验证此点是否变异，然后将这个假设的变异点从时间序列左侧向右侧滑动，以便找出所有可能的变异点。对每一变异点计算t检验统计量为：

要利用这个公式进行检验，即：

式中μ、n和分别表示样本序列的均值、样本量及标准差，而其下标l或r，则分别表示假设变异点的位置。

在以上计算基础上，找到tmax，即所有假设突变点的t值中的最大值；检验其显著性p(tmax)，置信度水平一般定为95％，而

其中η＝4.19lnn–11.54，而δ＝0.40。n为要分段的整个时间序列的长度，而ix(a,b)为不完全beta函数。如果p(tmax)达到95％显著性水平，则所假设的突变点即为统计意义上的突变点。在依据上述计算找到的突变点将时间序列分段后，再在分段后的时间序列中重复上述过程，直到没有突变点发现为止。

在此基础上，计算泛化相关指数，k为第k阶。对每一阶相关系数，都要计算局域相关系数及验证其显著性。在k阶，给定局域相关系数对应相应时间段长度为则可计算为：

而相应的检验统计量为：

而

根据的定义，此值等于1或-1，这种情况时，只有所有局域时段的相关为完全正相关与完全负相关，再结合相关检验统计量相关系数的显著性可用z检验进行验证。则即为泛化适应性相关系数。

检验统计量公式是：

其中，sign()为符号函数，当xi-xj小于、等于或者大于零时，sign(xi-xj)分别为-1、0和1；m-k统计量公式s大于、等于、小于零时分别：

z为正值表示增加趋势，负值表示减少趋势。z的绝对值在大于等于1.28、1.96、2.32时分别通过了信度90％、95％、99％显著检验。

实施例1，如图1、图2所示，为同一水文观测站实际观测的流量与水位过程，由此图可进一步证实，两个原本相关性极高的水文过程，由于人类活动以及气候变化，导致两个时序出现显著非平稳性，相关性在不同时段出现显著不稳定性，进一步证明我们此项计算算法发明的重大学术及实际应用价值。

基于不同时段长度以及尺度得出的局域化相关性量化指标，在此指标之上，由对数转化后，即可得出泛化相关性量化指标。

上述实施例仅为本发明技术方案的一种实现方式，不构成对本发明实施例的限定，本领域的技术人员在本发明公开的度分布设计方案的基础上，能够将其应用到其它的编译码方法中。