进行核燃料板弹簧压紧力模拟测定的方法与流程

本发明涉及核电核燃料性能分析技术领域，尤其是涉及一种进行核燃料板弹簧压紧力模拟测定的方法。

背景技术：

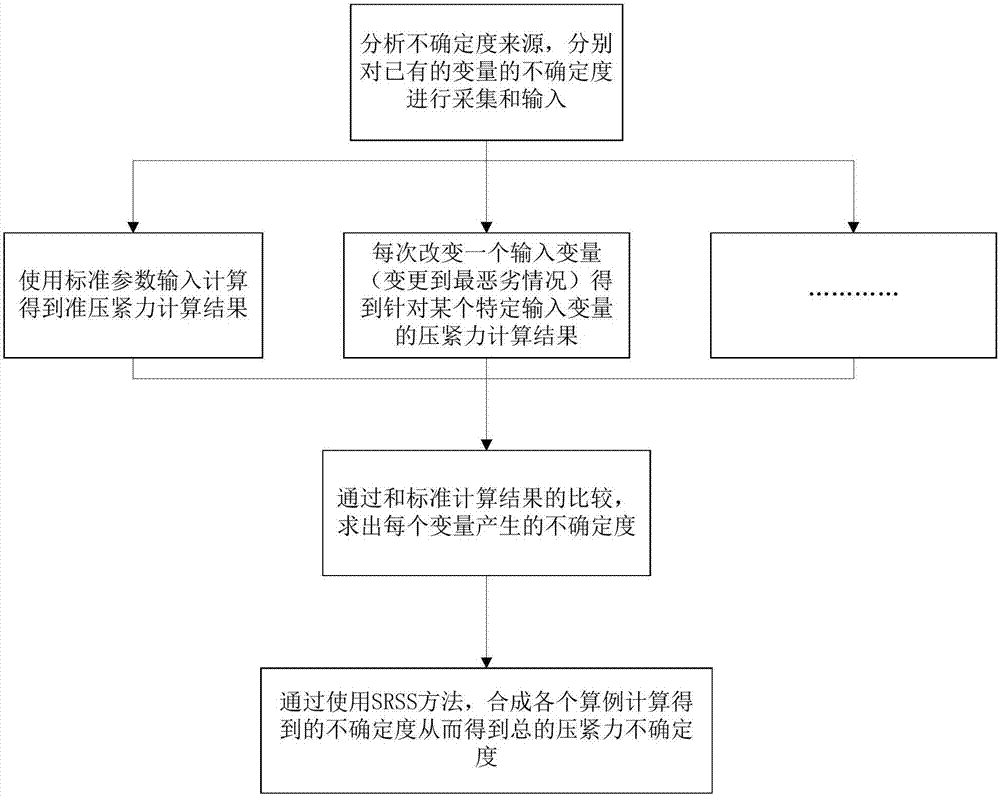
在燃料压紧力模拟测定过程中对不确定度的分析一直以来是采用gum方法(通用不确定度模拟测定方法)，通过对名义值进行模拟测定，然后通过一定的方法将不确定度进行叠加从而得到模拟测定结果的不确定度。具体流程如下：

gum方法压紧力模拟测定流程如图1所示。

此类gum分析方法具有很大的局限性，首先需要满足的以下假设：

1.假设输入量的概率分布呈对称分布；

2.假设输入量的概率分布近似为正态分布或者t分布；

3.测量模型为线性模型、可以转化为线性模型或者可用线性模型近似的模型。

这样的限制条件往往导致此种gum分析方法有很大的局限性。

技术实现要素：

本发明要解决的技术问题在于，针对现有技术中的上述缺陷，提供一种可以提高核燃料板弹簧压紧力的模拟测定结果科学性和准确度的模拟测定方法。

本发明解决其技术问题所采用的技术方案是：构造一种进行核燃料板弹簧压紧力模拟测定的方法，包括步骤：

s1：根据不确定度来源，获得影响压紧力的独立变量；

s2：选择压紧力测定工况状态点；

s3：在压紧力测定工况状态点下，对每个独立变量进行蒙特卡洛随机抽样，形成输入参数集合；

s4：将输入参数输入压紧力测定模型，得到对应的压紧力结果；

s5：重复多次s3、s4，得到多次压紧力测定结果，将电站的核燃料板弹簧设计基准的参数输入压紧力测定模型，得到设计基准压紧力结果，将多次压紧力测定结果与设计基准压紧力结果进行比较并统计比较结果，以获得压紧力总不确定度。

优选地，s3包括：利用随机数发生器产生一系列随机数，优选地，s2包括：

工况状态点由下述参数定义：电站的泵的体积流量、旁流、冷却剂密度、系统压力、堆芯功率、堆芯结构和燃耗。

优选地，工况包括电站的泵启动过程低温运行和超功率稳态的工作状况。

优选地，s3包括：

完成以下变量的不确定性传播：堆芯体积流量、压紧弹簧刚度、水力阻力、燃料组件湿重、跨距和/或弹簧压缩量；

其中，堆芯体积流量采用测量值拟合的正态分布来进行抽样；

压紧弹簧刚度采用实验值拟合的正态分布来进行抽样；

优选地，s5包括：根据多次压紧力测定结果得到压紧力的分布情况，得出压紧力正态分布的均值和方差。

实施本发明的技术方案，至少具有以下的有益效果：本发明可用于燃料组件性能分析上，可以对压紧力变化进行最接近真实的模拟测定，提高模拟测定结果的科学性和准确度。

附图说明

下面将结合附图及实施例对本发明作进一步说明，附图中：

图1是现有的gum方法压紧力模拟测定流程图。

图2是本发明的方法模拟测定核燃料压紧系统压紧力的流程图。

图3是本发明的方法基于本蒙特卡洛方法的模拟测定物理情景。

图4表示通过本发明方法中的物理模型模拟100000次得到的随机分布结果。

具体实施方式

为了对本发明的技术特征、目的和效果有更加清楚的理解，现对照附图详细说明本发明的具体实施方式。

如图2所示，本发明一个优选实施方式中的进行核燃料板弹簧压紧力模拟测定的方法，包括步骤：

s1：根据不确定度来源，获得影响压紧力的独立变量；

s2：选择压紧力测定工况状态点；

s3：在所述压紧力测定工况状态点下，对每个所述独立变量进行蒙特卡洛随机抽样，形成输入参数集合；

s4：将所述输入参数输入压紧力测定模型，得到对应的压紧力结果；

s5：重复多次s3、s4，得到多次压紧力测定结果，将电站的核燃料板弹簧设计基准的参数输入所述压紧力测定模型，得到设计基准压紧力结果，将所述多次压紧力测定结果与所述设计基准压紧力结果进行比较并统计比较结果，以获得压紧力总不确定度。

在一些实施例中，s3包括：利用随机数发生器产生一系列随机数，根据所述随机数，对每个所述独立变量进行蒙特卡洛随机抽样；所述随机数发生器提供一个任意的种子数，以保证每次的抽样值不相重复。随机正态或均匀分布的蒙特卡洛传播需要一个严密的数学模型，其中随机的抽样方法最为关键。如果随机正态分布期望为0，方差为1，可写为n[0，1]。均匀分布期望为0，半宽为1，可写为u[-1，1]。

该方法可用于燃料组件性能分析上，可以对压紧力变化进行最接近真实的模拟测定，提高模拟测定结果的科学性和准确度。其具体有以下有益效果：

1)本方法解决了确定论方法(gum方法)中无法给出不确定度的缺点。

2)本方法可以考虑来自各个方面的不确定度，可以详细的分析各个不确定度的来源和传播方式，方便扩展，能够提供更精确和更加贴近现实的各种变量的影响，最后的到得到准确的压紧力模拟测定结果。

3)结果可统计，可以使用任意置信度的结果，方便最终准则的调整。

4)本方法基于蒙特卡洛方法对输入变量进行抽样，针对每种组合进行了压紧力的模拟测定，并对其结果进行统计，这种方法更接近于现实情况，非常好的模拟了压紧力的真实情况，使得模拟测定结果更真实可信；

5)本方法实现了基本的全统计法模拟测定流程，同时方便拓展到其他参数的分析；

6)本方法流程清晰完整，方便今后编制程序，同时易于仿真分析。

在一些实施例中，s2包括：

所述工况状态点由下述参数定义：电站的泵的体积流量、旁流、冷却剂密度、系统压力、堆芯功率、堆芯结构和燃耗。通常，极限工况为低温度下的等温运行(冷却剂密度和流量大)。这个工况通常在电站启动(泵启动)和停闭(泵停转)。更极限的状态点为稳态超功率。优选地，所述工况包括电站的泵启动过程低温运行和超功率稳态的工作状况。

在一些实施例中，s3包括：

完成以下变量的不确定性传播：堆芯体积流量、压紧弹簧刚度、水力阻力、燃料组件湿重、跨距和/或弹簧压缩量。

其中，所述堆芯体积流量采用测量值拟合的正态分布来进行抽样；

所述压紧弹簧刚度采用实验值拟合的正态分布来进行抽样；

根据堆芯功率、堆芯流量和堆芯入口条件确定所述水力阻力系数；

根据燃料组件干重和排水体积和密度确定所述燃料组件湿重，取名义值；

所述跨距取名义值；

根据堆腔高度、燃料组件高度、辐照生长、热膨胀、弹簧自由高度、弹簧厚度确定所述弹簧压缩量。

在一些实施例中，所述s5包括：根据所述多次压紧力测定结果得到压紧力的分布情况，得出压紧力正态分布的均值和方差，作为其统计的关键参数，以便分析压紧力。

下面对这个方法进行详细的解释，这个方法的关键在于以下5步：

1)识别影响压紧力的独立变量；

2)开发模拟测定压紧力的模型，在模拟测定压紧力时，同时改变每个独立变量；

3)将每个独立变量的不确定性进行量化处理；

4)通过(2)的模型完成不确定性的蒙特卡洛传播，以获得压紧力总不确定性；

5)评估压紧力的公差范围，对最终的结果进行统计分析，得到其统计学关键参数。

使用本方法的优点：

1)各不确定度分量的大小可以不相接近

2)不确定度传播方式可以非常复杂，当模拟测定模型偏导数无法求得时同样适用

3)输出量的pdf可以不为正态分布和t分布

4)测量模型明显非线性也可以适用

5)输入量的pdf明显非对称也能适用

本蒙特卡洛方法的模拟测定物理情景，可以用图3进行描述。

下面对本发明的方法进行详细的进一步解释。本方法采用新的蒙特卡洛法(mcm)来进行不确定度的模拟测定。具体过程如图2所示。

一、识别影响压紧力的独立变量

模拟测定压紧力有两大类参数：

a)机械

影响压紧力的参数，包括：压紧弹簧刚度、燃料组件辐照生长、燃料组件热膨胀、冷停后的压紧弹簧厚度、燃料组件重力、燃料组件高度、上下堆芯板距离。

b)水力

影响水力载荷的参数，包括：冷却剂温度、堆芯入口流量分配不均匀性、部件压降系数、浮力、冷却剂流量(取决于泵的扬程曲线和冷却剂系统的水力抗性)。

对给定堆芯结构、燃料设计、运行工况和工况所处寿期，上述每个参数都有名义值。

给定堆芯结构、燃料设计、运行工况和工况所处寿期通过状态点体现。在以前的燃料组件压紧系统分析中，参数的不确定性采用确定论方法处理(除了获得弹簧压缩量的机械参数采用srss处理)。因此，确定论方法分析结果过于保守。另一方面，不确定性的统计学处理，对不确定性的联合作用后果提供一个更为合理的预测，减少了分析中的保守性。

二、模拟测定传播的物理模型

此物理模型和原有的模拟测定模型相同，可以继续使用原有压紧力模拟测定方法，即使用广核已经开发的软件系统(cactus)进行模拟测定。

其中需要输入的物理量如下：

(1)弹簧刚度

(2)堆腔高度

(3)燃料组件高度

(4)燃料组件热膨胀

(5)燃料组件辐照生长

(6)弹簧自由长度

(7)弹簧厚度

(8)弹簧松弛

(9)燃料组件体积(排水体积)

(10)冷却剂密度

(11)燃料组件重力

(12)水力升力

(13)堆芯体积流量

(14)组件跨距

决定平衡力的原始参数一共有14个。这14个原始参数中的某些可能不是统计学分布，或者在对参数的采样抽样过程会有差别，对于这种没法进行统计学分布描述的参数可以用恒量代替，或者近似统计抽样(或根据实际采样点数值)进行描述。

通过对整体的随机抽样进行多次模拟测定，最终得到压紧力结果，并对其进行统计学分析。

三、参数的随机抽样

随机正态或均匀分布的蒙特卡洛传播需要一个严密的数学模型，其中随机的抽样方法最为关键。如果随机正态分布期望为0，方差为1，可写为n[0，1]。均匀分布期望为0，半宽为1，可写为u[-1，1]。

使用模拟测定机语言的随机数发生器，产生介于正负之间的随机数。该发生器需要提供一个任意的种子数，以保证每次的抽样值不相重复。

随机正态分布的产生如下：

图4表示通过此模型模拟100000次得到的随机分布结果。

四、压紧力模拟测定工况状态点选择

通常，极限工况为低温度下的等温运行(冷却剂密度和流量大)。这个工况通常在电站启动(泵启动)和停闭(泵停转)。更极限的状态点为稳态超功率。

状态点由下述参数定义：体积流量、旁流、冷却剂密度、系统压力、堆芯功率、堆芯结构(燃料设计)和燃耗。

极限状态点的压紧力最小，其必须模拟测定的情况：泵启动过程低温运行和超功率稳态。

五、不确定性的传播

通过长期的工程经验和科学推论，总结出以下变量需要进行不确定性传播的考虑：堆芯体积流量、压紧弹簧刚度、水力阻力、燃料组件湿重(体积密度)、跨距、机械分析(弹簧压缩量)。

如果上述参数的不确定性不符合统计学分布，则采用保守值。

a)体积流量

对给定电站，名义堆芯体积流量≥测量流量。堆芯体积流量不确定性≥rcs流量测量不确定性。

模拟测定中采用测量值拟合的正态分布来进行抽样。

b)压紧弹簧刚度

对于给定组件，压紧弹簧刚度取决于弹簧系统的设计，该值可以根据实验获得。

模拟测定中采用实验值拟合的正态分布来进行抽样。

c)水力阻力系数

水力阻力系数，为复合参数，随状态点的改变而改变，取决于堆芯功率、堆芯流量和堆芯入口条件。水力参数包含了无量纲的压降系数(代表冲击压降和摩擦压降)。水力阻力的不确定性取决于冲击压降的不确定性。不确定性可以通过计算测量和预测之间的偏差，并通过多项式修正。

不包含不确定度。

d)燃料组件湿重，体积，密度

湿重取决于燃料组件干重和排水体积和密度。湿重变化很小，取名义值，不包含不确定性。

e)跨距

尺寸参数，用于计算压降。通常取名义值，不包含不确定性。

f)压紧弹簧变形

压紧弹簧变形取决于6个基本的尺寸参数，堆腔高度、燃料组件高度、辐照生长、热膨胀、弹簧自由高度、弹簧厚度。

燃料组件高度为下堆芯板与燃料组件接合处到上堆芯板与燃料组件接合处(通常为弹簧顶端)的距离。上述6个参数的名义值和不确定性来自于计算或测量。

六、确定最小压紧力

一旦状态点、参数和不确定性确定，就要检查电厂的设计基准算例。设计基准算例为采用核安全局批准的程序评价堆芯的热工水力状况，以获得每个燃料组件的压降。电站运行的典型工况定义了设计基准算例。

在给定的燃料设计，极限燃料组件在给定燃耗(如bol或eol)下有着最高的压降。在大多数情况下，弹簧系统的压紧能力和燃耗有关。保守的选择压紧能力最低的组件，以降低分析的数量。

通过热工水力程序预测设计基准算例得到的压降为：程序预测△pbasedesigncase：

基于rcs体积流量、堆芯旁流、燃料设计、堆芯功率水平、系统压力和入口冷却剂温度，冷却剂密度由堆芯平均温度确定。

程序预测了设计基准算例的压降，同时各个参数及其不确定性作为传播模型的输入。传播模型采用前述模型。

传播模型确定平衡力，要求计算10000次。压紧力的期望值和偏差在计算后即可获得。该状态点的平衡力在95％置信水平下，保持方向向下的概率为95％，计算公式为：

nhd95/95＝nhdmean-k95/95/n(σnhd)

其中，n＝10000

则nhd95/95＝nhdmean-k95/95/10000(σnhd)

其中，k95/95/10000＝1.670

在对每个状态点计算nhd95/95后，最小的nhd95/95值为极限工况。

因为得到了最终的压紧力分布数据，我们就可以对压紧力进行统计学处理，从而得到对应的统计量，以及我们要求的压紧力不确定度。

七、分析流程

在采用蒙特卡洛进行压紧力分析的分析过程如下：

a)定义分析的状态点；

b)定义原始变量的名义值和不确定性；

c)采用核安全局批准的程序和等于或接近于状态点的流量模拟测定堆内所有燃料组件压降，以定义设计基准算例；

d)采用传播模型(即使用已经进过验证的模拟测定软件，如cactus)，确定每个燃料组件的压紧力。如果每个燃料组件的合力为正(向下为正方向)，则压紧准则满足。其中具有最小压紧裕量的组件为所要分析的组件。

e)最终对所有的模拟测定结果进行统计分布，可以得出所需要的所有统计量，同时确定压紧力的不确定度。

八、方法的扩展

a)本发明实现了基本的全统计法模拟测定流程，同时方便拓展到其他参数的分析。

由于本方法采用蒙特卡洛抽样法实现，该方法使用抽样产生数据，只要需要参数的输入量及其统计分布规律就可以进行初始化数据输入进行整体模拟测定，而不需要考虑其中间过程的复杂性。对其最终的模拟测定结果仅需要进行统计学分析即可得到相关信息，所以大大降低了各类参数不确定度分析的难度。同时该方法具有普适性，可以推广应用于其他类似参数的模拟测定分析中。

b)本方法流程清晰完整，便于今后编制程序，同时易于仿真分析。

由于蒙特卡洛法基本思想就来源于计算机随机抽样模拟，便于进行编程仿真分析。其次本方法结构性强，循环清晰，逻辑严密，已经详细归纳出了其分析流程，便于后续方法的程序化。最后由于输入数据本身可独立修改，作到根据实际测量结果进行修正，极大地方便了燃料组件压紧力精确分析的实现。

以上所述仅为本发明的优选实施例而已，并不用于限制本发明，对于本领域的技术人员来说，本发明可以有各种更改、组合和变化。凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的权利要求范围之内。