基于小波变换维纳滤波和边缘检测的图像降噪方法与流程

本发明涉及一种图像处理技术，特别是一种基于小波变换维纳滤波和边缘检测的图像降噪方法。

背景技术

在微光条件下，由于光照较低以及探测器灵敏度等的限制，系统所获视频图像信噪比较低，影响人眼观察，甚至无法有效获得目标场景图像。微光视频的噪声主要由ccd所产生的符合高斯分布的白噪声和像增强器所产生的量子噪声所组成。

微光图像降噪算法主要分为空域滤波和变换域滤波两类，图像变换域去噪方法是对图像进行某种变换，将图像从空间域转换到变换域，再对变换域中的变换系数进行处理，再进行反变换将图像从变换域转换到空间域来达到去除图像嗓声的目的。将图像从空间域转换到变换域的变换方法很多，如傅立叶变换、沃尔什—哈达玛变换、余弦变换、k-l变换以及小波变换等。而傅立叶变换和小波变换则是常见的用于图像去噪的变换方法。空域滤波是在原图像上直接进行数据运算，对像素的灰度值进行处理。常见的空间域图像去噪算法有邻域平均法、中值滤波、低通滤波等。单独使用空域或者变换域滤波难以在降低图像噪声的同时保留图像边缘信息。因此，本文提出了一种在时域滤波的基础上进行空域滤波的时空域混合的微光视频滤波方法。

技术实现要素：

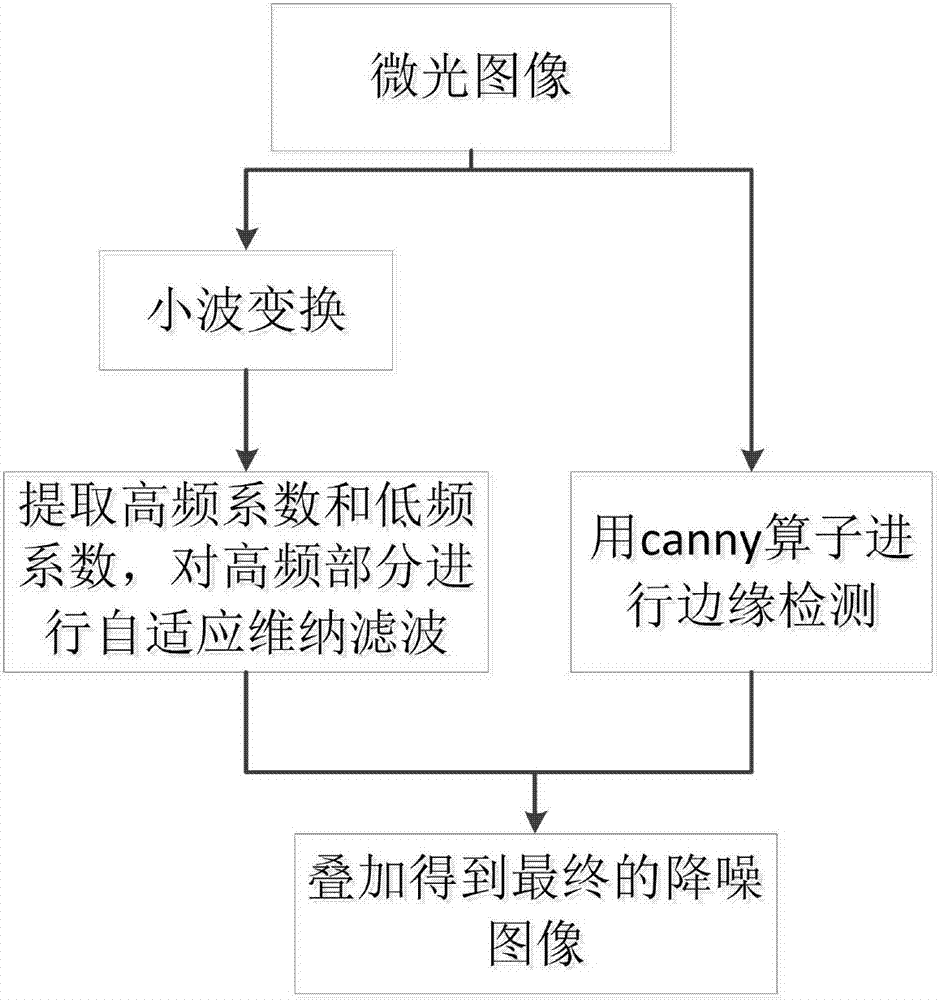
本发明的目的在于提供一种基于小波变换的改进的维纳滤波和边缘检测的微光图像降噪方法，本发明包括以下步骤：

步骤1，对原始的微光图像进行两层小波分解，提取第二层小波分解的近似系数和第二层小波分解的细节系数的水平分量、垂直分量、对角分量；

步骤2，选取合适的滤波窗口，通过改进的自适应维纳滤波降噪算法对图片进行降噪处理；

步骤3，在原图的基础上通过canny算子进行边缘检测，将检测出的边缘同经过维纳滤波后的重构图像进行叠加，得到最终的降噪图像。

本发明将空间域转换成小波域，选取合适的小波变换层数对含噪声图像进行自适应维纳滤波去噪，同时采用log边缘检测算子检测待降噪图像边缘，将图像分为边缘区和待降噪区，最后将边缘同小波重构后的图像降噪区叠加得到最终降噪图像。

下面结合说明书附图对本发明作进一步描述。

附图说明

图1为本发明基于小波变换的自适应维纳滤波和边缘检测的微光图像降噪算法流程图。

图2为基于小波变换的维纳滤波算法示意图。

图3为在0.10lux照度下人立于树林中微光成像实验示意图。

图4为在0.22lux照度下静止建筑物实验示意图。

图5为在0.22lux照度下微光移动人像实验示意图。

图6为在0.5lux照度下微光静止建筑物实验示意图。

具体实施方式

步骤1，对原始微光图像进行小波变换；

假设待处理的图像表示为y＝x+n；其中，x表示“干净”的图像，n是与x互不相关、均值为零、方差为σ²的高斯噪声矩阵。进行小波变换后可得：y＝x+n，式中y＝wy，x＝wx，n＝wn，w为小波变换的变换矩阵。由小波变换的正交性可知，n仍然是均值为零、方差为σ²的高斯变量，且与x互不相关。

步骤2，对待处理图像用’db2’小波函数进行两层小波分解，并提取第2层小波分解的近似系数(低频成分)，第2层小波分解的细节系数水平分量，第2层小波分解的细节系数垂直分量，第2层小波分解的细节系数对角分量。

对经过小波分解的待降噪图像的水平分量、垂直分量和对角分量分别进行自适应维纳滤波。

算法步骤如图2所示。

根据步骤1中所假设，待处理图像表示为y＝x+n；进行小波变换后可得：y＝x+n，式中y＝wy，x＝wx，n＝wn，w为小波变换的变换矩阵。由小波变换的正交性可知，n仍然是均值为零、方差为δ²的高斯变量，且与x互不相关。由于正交小波变换的去相关性，信号x经过正交小波变换以后的输出x也是不相关的，因此，我们也认为x是零均值的高斯随机变量，此时，维纳滤波的形式可简化为

其中e[·]表示变量的数学期望，a是维纳滤波系数，为x的最优线性估计。考虑到n与x互不相关，所以有

e[x²]＝e[y²]-δ²(2)

可以逐个求得e[y²]，对于位于坐标(i,j)处的e[y²]，可利用yi,j及其周围的值估计得到。为了不失一般性，利用一个(2r+1)×(2r+1)的方形窗(该窗的中心位于坐标(i,j)处)中对yi,j值平均求得

其中qi,j是方形窗内经过小波变换的像素内积和，qi,j是内积和均值，m是方形窗的大小。将qi,j作为的近似估计值，即代入(2)式可得

其中表示的数学期望，qi,j是数学期望的近似值，δ²是噪声方差。再代入(1)式，可得维纳滤波的各个系数为

由e[x²]≥0这个约束条件，所以(6)式可写成max(qi,j-δ²,0)。

现在定义维纳滤波的最小均方误差期望如下：

lmse＝e{[xi,j-ai,jyi,j]²}(7)

令bi,j＝δ²/qi,j，并由(6)可得

lsme＝e{[xi,j-(1-bi,j)(xi,j-ni,j)]²}(8)

为了简化，忽略各个下标，(8)式又可改写为

lsme＝e{[b(x+n)-n]²}(9)

当方形窗尺寸足够大时，可认为b与x和n是相互独立的。这一假设完全可以接受。将上式展开，根据数学期望的性质，并将(5)式代入(9)，可得

lmse＝e[b²]q+δ²{1-2e[b]}(10)

假设如果当：

lmse＞e[x²](11)

其中lmse是维纳滤波的最小均方误差期望，e[·]是变量的数学期望。则对于x的线性估计会变得很差，所以此时比较好的解决方案是将x直接赋0。

由代入(7)式可得

解上面的不等式，可得

q＜kδ²(13)

其中由于m取的典型值为9(3×3像素的图像块)，49(7×7像素的图像块)，所以k为1.47，1.20。即是说，当q小于kδ²时，放弃对x的线性估计，直接将x赋0，由此对图像完成基于小波分解的维纳滤波算法。

步骤2-2、将待降噪图像的小波变换的低频分量和经过自适应维纳滤波后的各方向分量进行叠加，采用’db2’小波函数重构得到降噪后的图像。

步骤3:使用canny算子对源图像进行边缘检测，将检测出的边缘图像同降噪后的图像进行叠加，得到最终降噪图像。

步骤3-1、canny算子具有低误码率、高定位精度和抑制虚假边缘等优点。在程序中，首先读入灰度微光图像，并采用canny算子进行边缘检测。在进行边缘检测时，采用函数自动计算的阈值，并返回该阈值，函数返回的阈值thresh为归一化后的阈值，得到对含噪原图进行边缘提取的边缘图像。

步骤3-2、将边缘图像同经小波域维纳滤波后的图像进行叠加得到最终的去噪图像。

实施例

本文选取了多个实验场景拍摄微光图像，分别对多种情况下拍摄的图像进行了实验验证。图3为在0.10lux照度下人立于树林中微光成像实验图像处理截图、图4为在0.22lux照度下静止建筑物微光成像实验图像处理截图、图5为在0.22lux照度下微光移动人像实验图像处理截图、图6为在0.5lux照度下微光静止建筑物实验图像处理截图。

可以看出本发明提出的一种基于小波变换的自适应维纳滤波和边缘检测的微光图像降噪算法克服了单一时空域滤波在滤除噪声的同时会将图像边缘等重要高频信息也滤除的缺点，在进行滤波的同时对含噪声图像的边缘进行了提取，有效地抑制了微光图像噪声，使得图像目标及背景轮廓更清晰，更便于信息的获取。