一种层状岩体隧道中光面聚能爆破参数的确定方法与流程

本发明涉及土木工程技术领域，具体是一种层状岩体隧道中光面聚能爆破参数的确定方法。

背景技术：

光面爆破是通过正确选择爆破参数和合理施工方法，分区分段微差爆破，使爆破后轮廓线符合设计要求的一种控制爆破技术。光面爆破技术因其能取得较理想的爆破面，不产生超挖，也不欠挖用等优点，被广泛用于隧道的爆破。聚能光面爆破是在光面爆破基础上，采用聚能装置使炸药的能量集中往预定爆破方向传递，从而达到更好的控制炸药能量释放，对隧道预定轮廓线的岩石进行切割，取得更为平整、理想的爆破面，正确确定周边眼爆破参数是爆出预设轮廓面的保证。但目前关于横观各向同性岩体中的爆破参数的确定以及结构面、节理裂隙发展方向对周边眼间距影响的理论研究成果还相对较少。

技术实现要素：

本发明的目的在于提供一种科学、精确的层状岩体隧道中光面聚能爆破参数的确定方法，解决在层状岩体中，由于结构面的存在导致光面爆破超挖严重，轮廓面不平整等问题。

为实现上述目的，本发明提供如下技术方案：

一种层状岩体隧道中光面聚能爆破参数的确定方法，包括以下步骤：

(1)炸药能量是沿四周均匀传递的，由于聚能缝的存在，爆炸时释放的能量分为两部分，一部分是向孔壁四周均匀传递的能量v1，其向四周产生四周内压p1，其中四周内压p1所积蓄的应变能为υε1，一部分是沿着切缝出汇集的能量v2，产生集中内压p2，所积蓄的应变能为υε2；爆轰产物对岩壁作用所积蓄的应变能υε由下式表示：

式中：ν——岩体的泊松比；

σ1、σ2、σ3——分别表示薄壁上任意点的环向应力、轴向应力以及径向应力；

e——岩体的弹性模量；

(2)假设影响因素λ，其中0≤λ≤1，影响因素λ与聚能管的材质、聚能缝宽度与长度有关，假设能量分配应按下式分配：

υε1＝(1-λ)υε

υε2＝λυε

(3)由四周内压p1产生的四周荷载f1按下式计算：

式中：α——其沿半径方向变化的一个微小角度，rad；

db——炮孔直径，m；

lc——装药长度，m；

将四周荷载f1分为两个方向的力，在x轴产生作用力和y轴产生作用力；在x轴产生作用力是作用在围岩侧对岩石的压应力；在y轴正方向产生作用力是作用于岩石临空面侧的拉应力；对四周荷载f1沿y轴方向进行积分，由四周荷载f1作用岩石产生的拉应力为：

式中：ee——周边眼间距，cm；

对四周荷载f1沿x方向进行积分，求四周荷载f1作用岩石产生的压应力为：

(4)由集中内压p2产生的集中荷载f2按下式计算：

由集中内压p2在岩壁上的产生的集中荷载f2的大小为：

式中：ρ0——炸药密度，g/cm³；

d——炸药爆速，m/s；

lb——炮孔长度，m；

dc——炸药直径，m；

θ——聚能缝缝宽所对应的圆心角，rad；

δ——薄壁圆筒的厚度；

n——爆破后产生气体碰撞岩壁时产生的应力增大倍数；

其拉应力用下式表示：

压应力表示：

在聚能管的作用下，四周荷载f1、集中荷载f2共同作用下对岩石产生的拉应力σy为：

由上面整理，得：

在x轴方向，四周荷载f1、集中荷载f2共同作用下对岩石的压应力σx为：

(5)假设结构面与两炮孔间的轮廓线夹角为βi，结构面上的正应力σγ与x轴夹角为：

γi＝|βi-90°|

其单元体在压应力σx与拉应力σy作用下，切应力τx为零，因此单元体在γ方向上正应力σγ与切应力τγ用下式表示：

当炸药爆炸作用于岩石产生的拉应力大于岩石的极限抗拉强度σp时，岩石将沿轮廓线发生y方向的拉破坏，且结构面方向上切应力小于岩石自身的抗剪强度；即破坏准则方程为：

σy≥σp

得出：

其中，——结构面的内摩擦角，c——结构面上的粘聚力。

作为本发明进一步的方案：影响因素λ的边界条件是：

①当λ＝0时，聚能管的刚度为零，该情况下的爆轰产物对岩壁的作用等同于一般爆破所对岩壁的作用，聚能管对爆破产生的影响不大；即p2＝0，p1＝p；

②当λ＝1时，聚能管材为刚性材质，能量集中于两侧聚能缝中扩散，即p1＝0。

作为本发明进一步的方案：γ、影响因素λ与周边眼间距ee的表达式为：

作为本发明进一步的方案：根据周边眼间距得出光面层厚度w为：w＝1.25ee。

与现有技术相比，本发明的有益效果是：

本发明根据结构面与周边眼间距所成角度计算不同角度，引入库伦与最大拉应力破坏准则，对不同影响因素下周边眼间距变化进行准确计算，将传统周边眼的参数确定根据实践经验类比提升至准确的计算得出聚能光面爆破周边眼的间距以及光面层厚度，该算法可以精确算出层状岩体中结构面与周边眼间距角度不同时，在不同的聚能管刚度λ影响下，其周边眼间距相应变化的合适取值。从而解决在层状岩体中超爆严重，开挖轮廓线不整齐，更简单准确的控制光面爆破开挖轮廓线。

附图说明

图1是聚能管结构示意图；

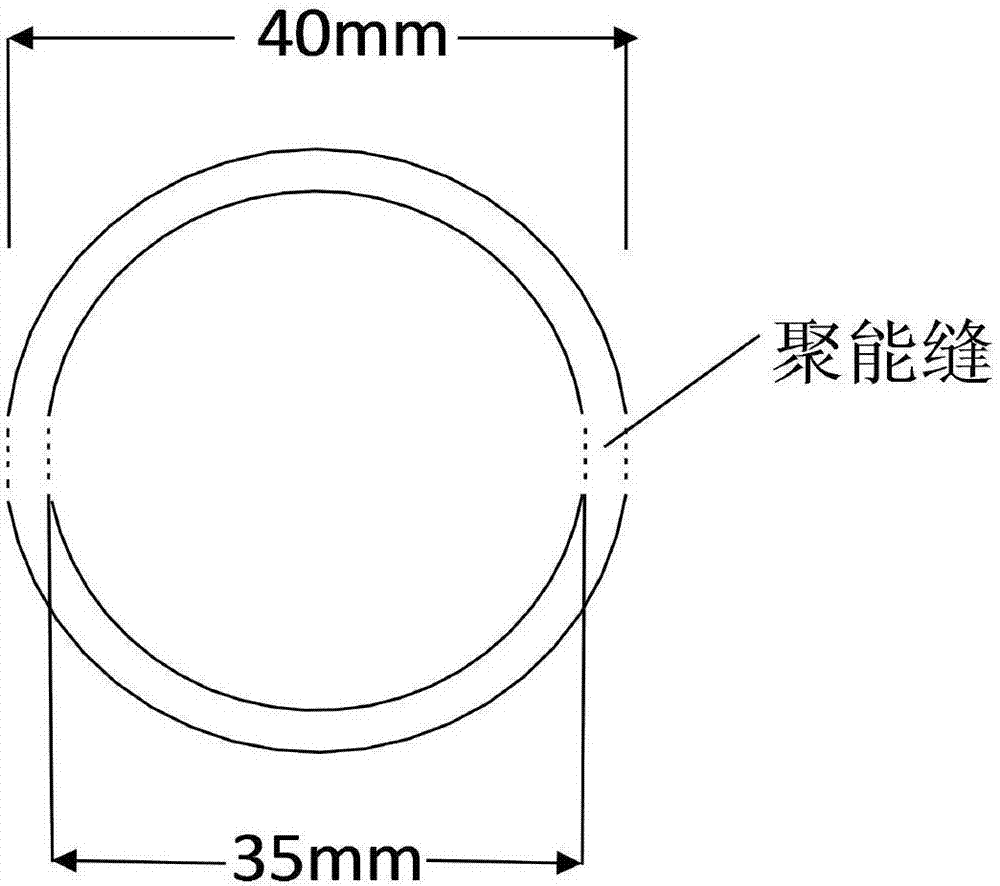
图2是图1的截面图；

图3是聚能爆破作用后的内压分布图；

图4是单元体受单向集中内压作用下的单元体应力状态图；

图5是单元体受均布内压作用下的单元体应力状态图；

图6两个炮孔间的周边眼间距示意图；

图7岩壁在受均布压力作用示意图；

图8岩壁受单向集中压力作用时产生横向拉应力的应力分布图；

图9两炮孔间距与层状岩体结构面所成角度示意图；

图10两炮孔间单元岩体所受应力示意图。

具体实施方式

下面将结合本发明实施例，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

实施例1

本发明对隧道聚能光面爆破参数确定的一种方法，下面结合附图和具体的算法进行详细说明。聚能光面爆破轮廓线上的炮眼(周边眼)是在其它炮眼爆破后最后起爆，周边眼采用聚能管装药，是炸药爆炸能量集中，使岩体沿开挖轮廓线爆出。本发明以长3.5m，直径36mm的pvc管为聚能管进行聚能缝切割(图1-2)，聚能切缝爆破是指将炸药爆炸时释放的能量沿着切缝槽穴汇集成聚能流，在切缝槽穴处产生高压、高速的高温射流，使之具有超强的穿透能力，从而对岩石进行切割，以获得较为平整的轮廓面。

一般光面爆破采用不耦合装药，不耦合装药时，爆轰波首先压缩聚能管与岩壁之间间隙内的空气，引起空气冲击波，而后再由空气冲击波作用于岩壁。因此，在对求作用于岩壁载荷时，假定：

(1)爆炸产物在间隙内的膨胀为绝热膨胀，其膨胀规律为pv³等于常数，遇岩壁激起冲击压力，并在岩石中引起爆炸应力波；

(2)忽略间隙内空气的存在(间隙较小)；

(3)爆轰产物开始膨胀时的压力按平均爆轰压力pm计算。

式中：ρ0——炸药密度(g/cm³)；d——炸药爆速(m/s)；

由式(1)得到，爆轰产物撞击岩壁前的炮孔内压的关系式为：

式中：

vc——炸药体积(m³)；vb——炮孔体积(m³)；

根据相关研究，爆轰产物撞击炮孔岩壁时，压力将明显增大，增大倍数n＝8～11。n——爆破后产生气体碰撞岩壁时产生的应力增大倍数。因此，炮孔岩壁受到爆轰压力为：

对隧洞掘进中钻孔柱装药：

式中：db——炮孔直径(m)；dc——炸药直径(m)；

lb——炮孔长度(m)；lc——装药长度(m)；

由式(3)和式(4)可得炮孔岩壁受到的爆轰压力为：

为分析问题方便起见，设炸药爆炸时对岩壁的压力是作用在一个两端封闭的薄壁圆柱形圆筒内，爆轰产物的传播是在圆筒内均匀传播，容器承受的内压压强为p，将岩壁看作一个理想弹塑体、可变形。相同得，薄壁容器视作理想弹塑性体。通过计算圆筒上任意点的应力分布状态，得出岩壁所积蓄的应变能υε。爆轰产物对岩壁作用所积蓄的应变能可由下式表示：

式中：ν——岩体的泊松比；

σ1、σ2、σ3——分别表示薄壁上任意点的环向、轴向以及径向应力；

e——岩体的弹性模量；

假设δ＜＜dc，δ为薄壁圆筒的厚度，纵截面上各点处的正应力σ1，该段圆筒表面y轴上的合力fy＝p·dc，由y轴的平衡方程关系得：

∑fy＝0，p·dc-2σ1×δ×1＝0(7)

按轴向拉伸计算其正应力σ2为；

径向的正应力σ3为：

σ3＝-p(9)

将(7)、(8)、(9)式代入(6)，可得爆轰产物对岩壁作用所积蓄的应变能νε值：

炸药能量是沿四周均匀传递的。但由于聚能缝的存在，爆炸时释放的能量分为两部分，一部分是向孔壁四周均匀传递的能量v1，其向四周产生四周内压p1，其中四周内压p1所积蓄的应变能为υε1，一部分是沿着切缝出汇集的能量v2，产生集中内压p2，所积蓄的应变能为υε2，其作用效果(图3)：

引入影响因素λ，λ的影响因素与聚能管的材质、聚能缝宽度与长度等因素有关即不妨假设能量分配应按下式分配：

υε1＝(1-λ)υε(11)

υε2＝λυε(12)

λ的边界条件是：

①当λ＝0时，聚能管的刚度为零，该情况下的爆轰产物对岩壁的作用等同于一般爆破所对岩壁的作用，聚能管对爆破产生的影响不大。即p2＝0，p1＝p。

②λ＝1时，即聚能管材为刚性材质，能量只往两侧聚能缝里扩散。即p1＝0。通过两种情况下的应变能相等来推导出p1，p2与p的关系。

因力与能量的可加性，可先对集中内压p2部分的所产生的应变能分析，圆筒两侧只受集中内压作用为p2，如图4(a)所示列x轴的平衡方程关系得：

圆筒横截面上各点处的正应力σ2相等，按轴向拉伸计算其正应力σ2′，由图4(b)得；

式中：a表示聚能缝宽度(mm)；

径向的正应力σ′3为：

σ3′＝-p2(15)

σ3′的绝对值远小于σ1′，所以近似的σ3′＝0。

由(13)、(14)、(15)可知，仅集中内压p2部分作用下圆筒的任意点处于单轴受拉状态，其应变能表达式应为：

由(10)、(12)、(16)可得集中内压p2的表达式：

在对四周内压p1部分的所产生的应变能分析，类比于一般爆破产生的应变能，如图5(a)所示列x轴的平衡方程关系得：

∑fy＝0，p1·dc-2σ1″×δ×1＝0(18)

按轴向拉伸计算，如图5(b)所示其正应力σ2″为；

径向的正应力σ3″为：

σ3″＝-p1(20)

将(18)、(19)、(20)式代入(6)，可得爆轰产物对岩壁作用所积蓄的应变能νε1值：

由(10)、(11)、(22)整理可得，四周内压p1的表达式：

将边界条件代入(17)、(23)，验证可得λ＝0时，p1＝p，p2＝0。λ＝1时，p1＝0，满足边界条件。

周边眼是沿轮廓线进行钻孔，因此，相邻两炮孔间的岩石受到炸药爆炸的作用对岩体进行切割，如图6所示。沿孔壁四周均匀分布作用于岩壁的四周内压p1，因此作用在四周的四周荷载f1向四周360°均匀扩散，因此可表示为：

根据(5)、(23)可以将(24)写成：

其中：α——其沿半径方向变化的一个微小角度(rad)；

建立直角坐标系(如图7)，将四周荷载f1分为两个方向的力，在x轴产生作用力和y轴产生作用力。在x轴产生作用力是作用在围岩侧对岩石的压应力，y轴产生作用力是作用于临空面侧对岩石的拉应力。由于岩石的抗拉强度为抗压强度的1/10～1/20，因而岩石大多都是受拉破坏。沿两炮孔间方向为x轴，垂直于x轴且指向岩石临空面侧为y轴，对四周荷载f1沿y方向进行积分，求四周荷载f1作用岩石产生的拉应力σy为：

式中：ee——周边眼间距(cm)；

由(26)、(25)整理可得：

对四周荷载f1沿x方向进行积分，求四周荷载f1作用岩石产生的压应力σx为：

将(25)代入(28)式可得：

由集中内压p2在岩壁上的产生的集中荷载f2简图(如图8(a))所示，在集中荷载f2的作用下，两炮孔间的岩石先是被挤压，而后由于集中荷载f2的作用，产生x轴方向的拉应力(图8(b))，岩石受拉破坏(根据文献岩石力学)，其集中荷载f2的大小可表示为：

式中：

θ——聚能缝缝宽所对应的圆心角(rad)

由(5)、(17)可将(30)写成：

其拉应力可用下式表示：

由(31)、(32)整理可得：

压应力可用(34)式表示：

将(31)代入(34)整理可得：

在聚能管的作用下，四周荷载f1、集中荷载f2共同作用下对岩石产生的拉应力为：

由式(27)、(33)、(36)整理，可得：

在x轴方向，四周荷载f1、集中荷载f2共同作用下对岩石的压应力为：

将(29)(35)代入(38)整理可得：

在横观各向同性的岩体中，岩石的破坏状态很大部分与结构面的发育有关，即结构面与两炮孔连线的之间的夹角不同，影响两炮孔的贯通裂缝产生。正是因为结构面的存在，岩体的破坏形式有三种情况：(1)沿两炮孔间的轮廓线发生y向拉断裂；(2)沿结构面发生剪切破坏；(3)同时发生沿两炮孔间轮廓线的拉断裂与沿层状岩体结构面的剪切破坏。

本发明假设结构面与两炮孔间的轮廓线夹角为βi，炮孔位置与层状岩体结构面发育不一致，导致结构面与两炮孔间的轮廓线夹角也不断变化如图9，取结构面与轮廓线之间的岩体分析，其单元体应力状态如图10所示。结构面上的正应力σγ与x轴夹角为：

γi＝|βi-90°|(40)

该单元体在主应力σx与σy作用下，切应力τx为零，因此单元体在γ方向上正应力σγ与切应力τγ可用下式表示：

由上述关系可知，显然在光面爆破中第二种与第三种爆破形式都对光爆效果有不同程度影响。若在层状岩体中要达到良好的光爆效果即发生第一种破坏形式，当炸药爆炸作用于岩石产生的拉应力大于岩石的极限抗拉强度时，岩石将沿轮廓线发生y方向的拉破坏，且结构面方向上剪切应力小于岩石自身的抗剪强度。因此，可以通过破坏关系有：

σy≥σp(43)

式中：——结构面的内摩擦角，c——结构面上的粘聚力

将(37)代入(43)可得：

将(37)、(39)、(40)、(41)、(42)代入破坏准则方程(44)中整理可得：

将(46)换一种表达可得γ、λ与周边眼间距ee的表达式：

周边眼间距ee与光面层厚度的关系通常以密集系数k来表示，其大小对光面爆破效果有较大影响，其关系为：

理论和实践均证明光面爆破炮眼间距与光面层厚度之比取0.8较为适宜，因此，光面层厚度为：

w＝1.25ee(49)

式中：w——光面层厚度(cm)；

考虑到需要同时满足破坏准则(45)、(47)即能使破裂面沿两炮孔轮廓线，因此可得周边眼间距ee、光面层厚度w与λ、γi的关系可查附表1。

表1

对于本领域技术人员而言，显然本发明不限于上述示范性实施例的细节，而且在不背离本发明的精神或基本特征的情况下，能够以其他的具体形式实现本发明。因此，无论从哪一点来看，均应将实施例看作是示范性的，而且是非限制性的，本发明的范围由所附权利要求而不是上述说明限定，因此旨在将落在权利要求的等同要件的含义和范围内的所有变化囊括在本发明内。

此外，应当理解，虽然本说明书按照实施方式加以描述，但并非每个实施方式仅包含一个独立的技术方案，说明书的这种叙述方式仅仅是为清楚起见，本领域技术人员应当将说明书作为一个整体，各实施例中的技术方案也可以经适当组合，形成本领域技术人员可以理解的其他实施方式。