一种梯级泵站调水工程甩站优化调度方法与流程

本发明涉及一种梯级泵站调水工程甩站优化调度方法，是一种梯级泵站调水工程优化调度技术，是一种在小流量输水工况下可节能增效的甩站优化调度方法。

背景技术：

梯级泵站调水工程是解决区域性水资源供需矛盾，实现水资源合理配置的重要手段。采用优化调度技术实现梯级泵站调水工程的安全稳定和高效经济运行，是泵站优化调度研究的重点问题。梯级泵站调水工程优化调度常针对特定的运行工况，采用适当的优化算法，对系统流量、扬程进行优化分配。但现有的调度方法忽略了一种情况，即：在工程试运行期或水源地可供水量较少时，渠道输水流量一般低于设计流量，沿程和局部水力损失均会减小，导致梯级泵站实际提升的扬程降低。在这种情况下，如果按照常规启动所以泵站进行调控，开启了过多的泵站提升扬程，这实际是一种浪费。如何解决这个问题，以期找到更加简单和能够节约能源的调度方法是需要解决的问题。

技术实现要素：

为了克服现有技术的问题，本发明提出了一种梯级泵站调水工程甩站优化调度方法。所述的方法通过优化调度方法，在水量较小的情况下，以甩站的方式，减少泵站开启，简化调度，降低运营成本。

本发明的目的是这样实现的：一种梯级泵站调水工程甩站优化调度方法，所述方法的步骤如下：

对泵站进行甩站可行性分析的步骤：建立水力学模型，试算渠段稳态水面线，对各级泵站进行甩站可行性分析，过程如下：

逐次构造各级泵站离散计算工况点：

具有m梯级泵站的调水工程，则m级泵站形成m-1个渠池，输水过程中全线流量匹配，离散梯级泵站可运行流量区间qmin，qmax，得到等步长流量离散序列q1，q2，……qs-1，qs，离散步长可调；离散各级泵站进水侧水位控制区间zi,min，zi,max，其等步长离散序列为zi,1，zi,2，……zi,t-1，zi,t，离散步长可调；由流量序列和水位序列组合得到第i级泵站离散计算工况点集，其中：i=2，……，m；

利用水力学模型试算各种工况下的渠段稳态水面线，并判断甩站可行性：

耦合构筑物相容方程和恒定流st.venant方程组，构建水力学模型，采用preissmann格式离散方程组，并用双扫描法求解模型；

对第i级泵站进行甩站运行可行性分析，采用水力学仿真模型，模拟第i+1级泵站至第i-1级泵站之间渠段在各种工况下的水面线；

判断是否可以甩站的步骤：选取第i+1级泵站进水侧水位zi+1,in为下游边界，第i-1级泵站输水流量qi-1为上游边界，在全线流量匹配条件下qi+1=qi-1，模拟工况点即为第i+1级泵站离散工况点qi+1，zi+1,in；

以第i-1级泵站出水侧水位控制区间zi-1,outmin，zi-1,outmax为判断条件，若模拟得到的第i-1级泵站出水侧水位zi-1,out在其水位控制区间内，即zi-1,outmin≤zi-1,out≤zi-1,outmax，则第i级泵站可以甩站运行，并进入下一步骤；否则，则第i级泵站无法甩站运行，并退出；

形成甩站运行可行域的步骤：拟合可甩站运行临界工况点，形成甩站运行可行域，过程如下：

当第i级泵站可甩站运行时，对离散的输水流量序列，统计相应于各流量的第i+1级泵站进水侧甩站临界水位，分别拟合可甩站运行最高、最低临界工况点，得到第i级泵站甩站运行时，第i+1级泵站进水侧临界水位与流量的函数关系式：

zi+1,dmin=fmin（q），zi+1,dmax=fmax（q），

甩站临界水位-流量曲线与泵站固有的流量、水位约束共同形成甩站运行可行域；

构建甩站优化调度模型的步骤：采用动态规划算法，在甩站可行域内求解模型，得到甩站优化调度方案，过程如下：

选择优化调度模型的目标函数，以总能耗最小为目标函数：

式中：n表示梯级泵站总功率；ni表示第i级泵站参与运行的机组数；ρ为水的密度；g为重力加速度；qi，j表示第i级泵站第j台机组的提水流量；ηi，j表示第i级泵站第j台机组的效率；hi为第i级泵站的提水扬程；

构造甩站优化调度的约束条件：

第i级泵站的扬程约束：hi，min≤hi≤hi，max；

第i级泵站进水侧水位约束：zi，inmin≤zi，in≤zi，inmax；

第i级泵站出水侧水位约束：zi，outmin≤zi，out≤zi，outmax；

第i级机组抽水功率约束：0≤ni≤ni，max；

第级泵站流量约束：qi，min≤qi≤qi，max；

若第i级泵站甩站运行，则该级泵站的扬程约束为：hi，min≤hi≤hi，max或hi=0；当第i级泵站甩站时，第i+1级泵站进水侧水位约束修正为甩站水位约束，即：

max（zi+1，dmin，zi+1，inmin）≤zi+1，in≤min（zi+1，dmax，zi+1，inmax）；

优化调度结果的步骤：动态规划算法求解甩站优化调度模型：

将梯级泵站的每一级看作一个阶段，故阶段变量为i；第i阶段至最末阶段m的累积扬程si为状态变量；第i级泵站的提水扬程hi为决策变量；

根据动态规划算法建立状态转移方程和动态规划递推方程：

状态转移方程：si+1=si－hi+hfi，hfi表示第i渠段的水力损失；

动态规划递推方程：

fi（si）=min{ni（qi，hi）+fi+1（si－hi+hfi）}；

构建甩站调控模型的步骤：以优化调度方案为调控目标，采用控制蓄量法获取满足安全标准的经济调控方案，过程如下：

转换调控目标为模型约束：

设第i级泵站需要甩站运行，当前时刻第i级泵站进水侧水位为z1c，第i+1级泵站进水侧水位为z2c，两级泵站输水流量均为qic；

甩站目标：第i级泵站进水侧水位为z1d，第i+1级泵站进水侧水位为z2d，两级泵站输水流量为均qid；

通过各渠段的水位-流量-蓄量关系计算，得到第i级泵站站前渠池的蓄量变化量为δv1，第i级泵站站后渠池的蓄量变化量为δv2，同时还可计算得到站后渠池15cm最小蓄量变化量δv2（15cm）min；由此可得第i+1级泵站的允许最大抽水流量：

qi+1，max=δv2（15cm）min/3600；

形成甩站调控方案的步骤：计算有约束条件下的最节能调控方案：

考虑甩站运行时，节制闸的开启条件，要求甩站运行泵站的配套节制闸闸前、闸后在同一时间达到同一水位。即：

式中，t为甩站调控过程中，由当前工况调整到甩站工况的时间；t1为站前渠池，由当前工况调整到甩站工况的时间；t2为站后渠池，由当前工况调整到甩站工况的时间；

第i－1级泵站t时刻的功率为：

式中，h（t）i－1为i时刻第i－1级泵站的扬程；η（t）i－1为i时刻第i－1级泵站的效率；

第i+1级泵站t时刻的功率为：

式中，h（t）i+1为t时刻第i+1级泵站的扬程；η（t）i+1为t时刻第i+1级泵站的效率；

第i级泵站甩站调控总费用为：

式中，td为第i级泵站甩站，第i+1和第i－1级泵站工况调整的总费用；p为单位电价；

将qi-1通过时间关系转换为qi+1的函数，并将td对qi+1求导，得到满足安全约束的最节能调控方案：

第i+1级泵站最优输水流量qd，i+1，第i－1级泵站最优输水流量qd，i－1，甩站调控时间t。

本发明产生的有益效果是：本发明所述方法在梯级泵站调水工程中，建立水力学模型，试算渠段稳态水面线，对各级泵站进行甩站可行性分析，得到甩站运行可行域；构建甩站优化调度模型，采用动态规划算法，在甩站可行域内求解模型，得到甩站优化调度方案；构建甩站调控模型，以优化调度方案为调控目标，采用控制蓄量法获取满足安全标准的经济调控方案。本发明建立适用于梯级泵站调水工程在工程试运行期或水源地可供水量较少时，小流量输水工况下的甩站优化调度方法，能够根据实际工况优化参与调水的泵站级数，降低运行成本；同时优化甩站相邻泵站的运行工况，合理分配泵站扬程，进一步节能降耗，为实际调度提供科学依据和技术支撑。

附图说明

下面结合附图和实施例对本发明作进一步说明。

图1是本发明的实施例一所述梯级泵站调水工程甩站运行方法的示意图；

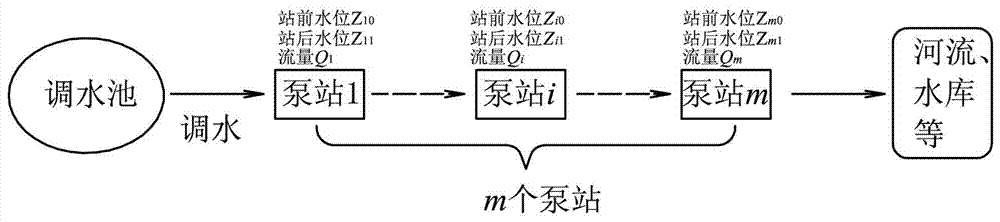
图2是梯级泵站调水工程示意图；

图3是本发明的实施例一所述的方法的流程图；

图4是本发明的实施例一所述的第i级泵站甩站运行可行域示意图；

图5是本发明的实施例一所述的甩站调控示意图。

具体实施方式

实施例一：

本实施例是一种梯级泵站调水工程甩站优化调度方法。所谓“甩站”就是通过减少参与运行的泵站级数，实现系统节能增效的运行方式，即某级泵站不运行，通过调整该级泵站前、后渠池的水位关系，使水流直接经上一级泵站提水后靠重力自流到下一级泵站。如图1中有三个泵站，图1中标示为1的泵站i，图1中标示为2的泵站i－1，图1中标示为3的泵站i+1。图1中还标示了正常运行的最低水面线4和正常运行的最高水面线5，图1中用阴影部分表示可以实现甩站运行的区域，不运行中间的一个泵站（图1中用虚线表示的泵站i标示为1），使泵站i－1和泵站i+1之间形成了甩站运行的水位状态，图1中标示了甩站运行的最高水面线6，和甩站运行的最低水面线7，以此节约运营成本，提高调控效率。

本实施例的基本原理为：

梯级泵站调水工程如图2所示。该系统由m个泵站和m－1个渠段组成，假设首级泵站的进水侧水位和末级泵站的出水侧水位在短时间内不变，并且全线输水流量匹配。各级泵站进、出水侧水位和系统输水流量均为已知。

针对上述调水工程中，建立水力学模型，试算渠段稳态水面线，对各级泵站进行甩站可行性分析，得到甩站运行可行域；构建甩站优化调度模型，采用动态规划算法，在甩站可行域内求解模型，得到甩站优化调度方案；构建甩站调控模型，以优化调度方案为调控目标，采用控制蓄量法获取满足安全标准的经济调控方案。

本实施例所述方法的具体步骤包括（梯级泵站调水工程甩站优化调度流程见图3）：.

（一）对泵站进行甩站可行性分析的步骤：首先，建立水力学模型，试算渠段稳态水面线，对各级泵站进行甩站可行性分析，获取甩站运行可行域，过程如下：

1.逐次构造各级泵站离散计算工况点：

假设梯级泵站调水工程共有m级泵站，则由该m级泵站形成m－1个渠池。输水过程中认为全线流量匹配，离散梯级泵站可运行流量区间（qmin，qmax），得到等步长流量离散序列q1，q2，……qs-1，qs，离散步长可调。离散各级泵站进水侧水位控制区间（zi,min，zi,max）（以第i级泵站为例），其等步长离散序列为（zi,1，zi,2，……zi,t-1，zi,t），离散步长可调。由流量序列和水位序列组合得到第i（i=2，……，m）级泵站离散计算工况点集：

2.利用水力学模型试算各种工况下的渠段稳态水面线，并判断甩站可行性：

由于模拟的是稳态（恒定流）水面线，故对st.venant方程组进行简化，除去水力要素随时间的偏导项，得到恒定流st.venant方程组。耦合构筑物相容方程和恒定流st.venant方程组，构建水力学模型，采用preissmann格式离散方程组，并用双扫描法求解模型。

假设对第i级泵站进行甩站运行可行性分析，采用水力学仿真模型，模拟第i+1级泵站至第i－1级泵站之间渠段在各种工况下的水面线。

（二）判断是否可以甩站的步骤：选取第i+1级泵站进水侧水位zi+1,in为下游边界，第i－1级泵站输水流量qi-1为上游边界，在全线流量匹配条件下（qi+1=qi-1），模拟工况点即为第i+1级泵站离散工况点（qi+1，zi+1,in）。

以第i－1级泵站出水侧水位控制区间（zi-1,outmin，zi-1,outmax）为判断条件，若模拟得到的第i－1级泵站出水侧水位zi-1,out在其水位控制区间内，即zi-1,outmin≤zi-1,out≤zi-1,outmax，则第i级泵站可以甩站运行；否则，则第i级泵站无法甩站运行。

（三）形成甩站运行可行域的步骤：拟合可甩站运行临界工况点，形成甩站运行可行域：

当第i级泵站可甩站运行时，对离散的输水流量（qi=qi+1=qi-1）序列，统计相应于各流量的第i+1级泵站进水侧甩站临界水位。分别拟合可甩站运行最高、最低临界工况点，得到第i级泵站甩站运行时，第i+1级泵站进水侧临界水位与流量的函数关系式：

zi+1,dmin=fmin（q），zi+1,dmax=fmax（q）。

甩站临界水位-流量曲线与泵站固有的流量、水位约束共同形成甩站运行可行域（见图4）。

（四）构建甩站优化调度模型的步骤：采用动态规划算法，在甩站可行域内求解模型，得到甩站优化调度方案，过程如下：

1.选择优化调度模型的目标函数：

梯级泵站调水工程的目标函数通常为泵站总效率最高或总能耗最小。以总能耗最小为例：

式中：n表示梯级泵站总功率，kw；m表示梯级泵站总级数；ni表示第i级泵站参与运行的机组数；ρ为水的密度，取为1.0×10³kg/m³；g为重力加速度，取为9.8n/kg；qi，j表示第i级泵站第j台机组的提水流量；ηi，j表示第i级泵站第j台机组的效率；hi为第第i级泵站的提水扬程。

2.构造甩站优化调度的约束条件：

第i级泵站的扬程约束：hi，min≤hi≤hi，max；

第i级泵站进水侧水位约束：zi，inmin≤zi，in≤zi，inmax；

第i级泵站出水侧水位约束：zi，outmin≤zi，out≤zi，outmax；

第i级机组抽水功率约束：0≤ni≤ni，max；

第i级泵站流量约束：：qi，min≤qi≤qi，max；

若第i级泵站甩站运行，则该级泵站的扬程约束为：hi，min≤hi≤hi，max或hi=0；当第i级泵站甩站时，第i+1级泵站进水侧水位约束修正为甩站水位约束，即:

max（zi+1，dmin，zi+1，inmin）≤zi+1，in≤min（zi+1，dmax，zi+1，inmax）。

（五）优化调度结果的步骤：动态规划算法求解甩站优化调度模型：

梯级泵站甩站优化调度是一个多阶段决策过程，采用工程中常用的动态规划算法对模型进行求解。将梯级泵站的每一级看作一个阶段，故阶段变量为i；第i阶段至最末阶段m的累积扬程si为状态变量；第i级泵站的提水扬程hi为决策变量。根据动态规划算法建立状态转移方程和动态规划递推方程：

状态转移方程：：si+1=si－hi+hfi，hfi表示第i渠段的水力损失。

动态规划递推方程：

fi（si）=min{ni（qi，hi）+fi+1（si－hi+hfi）}。

梯级各泵站内部一般采用性能相同的机组，故采用平均分配原则制定站内流量分配方案。采用上述方法进行优化求解，寻找最优的梯级水位组合。

（六）构建甩站调控模型的步骤：以优化调度方案为调控目标，采用控制蓄量法获取满足安全标准的经济调控方案，过程如下：

转换调控目标为模型约束：

甩站是一种主动调整运行方式的行为，并非应急工况，渠道中水位降幅需要满足每小时不超过15cm的要求，甩站调控示意见图5。

假设第i级泵站需要甩站运行，当前时刻第i级泵站进水侧水位为z1c（图5中标示为9的水面线），第i+1级泵站进水侧水位为z2c（图5中标示为8的水面线），两级泵站输水流量均为qic。甩站目标：第i级泵站进水侧水位为z1d（图5中标示为10的水面线，与第i—1级泵站进水侧水位相等），第i+1级泵站进水侧水位为z2d，两级泵站输水流量为均qic。通过各渠段的水位-流量-蓄量关系计算，得到第i级泵站站前渠池的蓄量变化量为δv1，第i级泵站站后渠池的蓄量变化量为δv2（站后渠池为水位下降渠池），同时还可计算得到站后渠池15cm最小蓄量变化量δv2（15cm）min。由此可得第i+1级泵站的允许最大抽水流量：

qi+1，max=δv2（15cm）min/3600。

（七）形成甩站调控方案的步骤：计算有约束条件下的最节能调控方案：

考虑甩站运行时，节制闸的开启条件，要求甩站运行泵站的配套节制闸闸前、闸后在同一时间达到同一水位。即：

，

式中，t为甩站调控过程中，由当前工况调整到甩站工况（开启配套节制闸）的时间；t1为站前渠池，由当前工况调整到甩站工况的时间；t2为站后渠池，由当前工况调整到甩站工况的时间；其余含义同上。

第i－1级泵站t时刻的功率为：

式中：ρ为水的密度，取为1.0×10³kg/m³；g为重力加速度，取为9.8n/kg；h（t）i－1为t时刻第i－1级泵站的扬程；η（t）i－1为t时刻第i－1级泵站的效率。

第i+1级泵站t时刻的功率为：

式中，h（t）i+1为t时刻第级泵站的扬程；η（t）i+1为t时刻第i+1级泵站的效率；其余含义同上。

第i级泵站甩站调控总费用为：

式中，td为第i级泵站甩站，第i+1和第i－1级泵站工况调整的总费用，元；p为单位电价，元/千瓦时；其余含义同上。

为得到在最少费用时的调控方案，该问题转换为复合函数的极值问题。将qi-1通过时间关系转换为qi+1的函数，并将td对qi+1求导，得到满足安全约束的最节能调控方案：qd，i+1（第级泵站最优输水流量），qd，i－1（第i－1级泵站最优输水流量），t（甩站调控时间）。

最后应说明的是，以上仅用以说明本发明的技术方案而非限制，尽管参照较佳布置方案对本发明进行了详细说明，本领域的普通技术人员应当理解，可以对本发明的技术方案（比如模型的选择、各种公式的运用、步骤的先后顺序等）进行修改或者等同替换，而不脱离本发明技术方案的精神和范围。