一种基于分形维值的断层带渗透性定性评价方法与流程

本发明涉及煤系承压断层带渗透性研究领域，具体涉及一种基于分形维值的断层带渗透性定性评价方法。

背景技术：

断层作为岩体内的缺陷结构，在其影响带内岩石破碎、松散、裂隙发育，是煤层和下伏承压含水层发生联系的主要途径。断层破碎带岩石的渗透性是表征断层富水性及导水性的重要指标，同时也是影响地下工程中由渗流失稳而引发灾害事故的重要影响因素之一，因此对断层渗透性评价至关重要。目前对断层渗透性评价大多采用试验方法，此方法操作较为繁琐。

本发明基于断层泥是由断层反复运动时两盘岩石的挤压、碎裂、摩擦、滑动作用与地下水携带物质的沉淀等作用形成的，蕴含了有关断层运动和性质的大量信息，且近年国际国内一些学者研究发现，不同岩石介质及力学环境中形成的断层泥有着不同的分维，对断层渗透性进行定性评价。

技术实现要素：

1.本发明的目的

鉴于此，本发明针对断层渗透性评价方法的不足，提供一种更能定性评价断层渗透性的方法。

2.本发明的技术方案

为实现上述目的，本发明一种基于分形维值的断层带渗透性定性评价方法，该方法包括：步骤a，以断层泥样品颗粒粒径为对象，绘制m(r)/m与粒径r的线性拟合图；步骤b，根据线性拟合图，结合相关公式，求出拟合公式；步骤c，根据线性拟合公式，求解断层泥岩样分形维值d；步骤d，根据所得分维值的大小，判断断层带粘粒含量，以此定性评价断层带渗透性。

本发明以断层泥颗粒粒径为研究对象，借助分形维值d来定性评价断层带的渗透性的方法较为新颖，且操作简单，易于实际应用，为断层带渗透性评价提供了一种新的方法和思路。

附图说明

此处用来说明的附图是为了对本发明的进一步解释和说明，为本申请的一部分，但并不能限定本发明。

图1为本发明基于分形维值的断层带渗透性定性评价方法流程图。

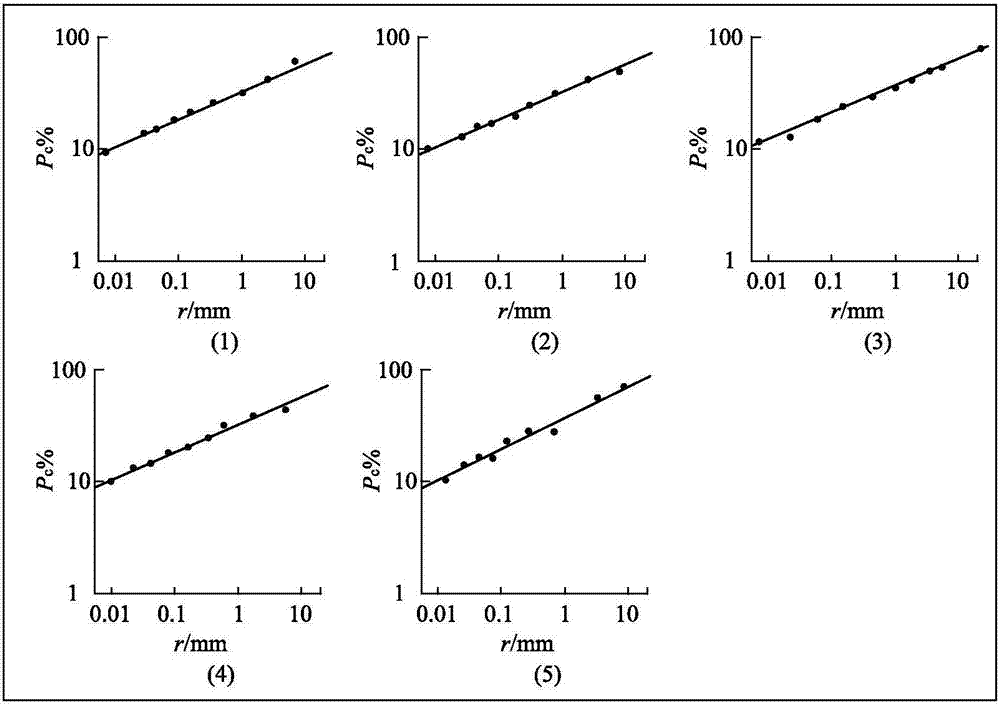
图2为本发明实例某断层m(r)/m与粒径r的线性拟合图。

图3为本发明实例某断层泥分形维值与细颗粒物质关系散点图。

具体实施方案

下面结合附图及本发明所应用的实例，对本发明进行进一步说明。

图1为本发明基于分形维值的断层带渗透性定性评价方法流程图。如图1所示，该方法包括：

步骤a，以断层泥样品颗粒粒径为对象，绘制m(r)/m与粒径r的线性拟合图；

步骤b，根据线性拟合图，结合相关公式，求出拟合公式；

步骤c，根据线性拟合公式，求解断层泥岩样分形维值d；

步骤d，根据所得分维值的大小，判断断层带粘粒含量，以此定性评价断层带渗透性。

以下结合具体实例，对上述每一步骤进行解释说明。

步骤a，以断层泥样品颗粒粒径为对象，绘制m(r)/m与粒径r的线性拟合图。在本发明实例中，根据某断层泥样品颗粒粒径为对象，绘制m(r)/m与粒径r的线性拟合图，见图2。

步骤b，根据线性拟合图，结合相关公式，求出拟合公式。

断层泥分形分析原理：

自然界中物质形态、功能、信息及时空结构等方面在局部与整体性上往往显示出自相似性，在分形学中可用一种基于hausdorff-besicovitch空间的连续变化非整数的分形维数(简称“分维”)d表示空间维数，从而产生了测度观的转变，为研究自然界中的复杂现象提供了一种科学方法。目前分形学方法在地学领域被日益广泛应用。

细粒沉积物颗粒分布在统计上通常具有一定的自相似性，称为统计分形。对应于不同类型和性质的物质颗粒指标的某些特征用分形学的分维法描述，可显示出空间维数上的不同分维d：

logn(r)＝-dlogr+c(1)

设沉积物颗粒的平均粒径为r，粒径小于r的颗粒累积质量为m(r)，m为样品总质量，根据经验，相对累计质量m(r)/m与r的关系式往往满足式(2)，即

log(m(r)/m)＝blogr+a(2)

假定沉积物颗粒固体密度均匀分布，则颗粒质量正比于颗粒粒径立方，即频度的增量与质量的增量关系为：

联立(1)～(3)式，可得到：

(4)式的意义是：如果沉积物的粒度组成确有分形特征，则在双对数坐标下，可得到确切d值。注意到3-d在公式中是一个线性比例系数，因此当对某个具体样品颗粒成分依据(4)式进行相关分析，如果线性相关系数高，意味着样品颗粒分形特征明显。

在本发明实例中，以某断层破碎带断层泥颗粒粒径为对象(见表1)，根据(4)式在双对数坐标系建立pc＝m(r)/m与r线性拟合关系，拟合出5条曲线的方程，分别为：

①y＝1.901+0.181x；②y＝1.892+0.175x；③y＝1.613+0.305x：

④y＝1.862+0.171x；⑤y＝1.885+0.108x

步骤c，根据线性拟合公式，求解断层泥岩样分形维值d。

本发明实例中，根据步骤b，5个线性拟合公式，求出5个样品的分维d分别为2.912、2.863、2.709、2.827和2.872，见表1。

步骤d，根据所得分维值的大小，判断断层带粘粒含量，以此定性评价断层带渗透性。

对比图2中(1)～(5)可看到，由于粒径分布右端点都对应于pc＝100％，因此左端的pc值(即“粘粒含量”)实际控制了直线斜率；当粘粒含量多时，直线斜率较缓，即3-d较小，因此d自然较大。对表1的粘粒含量和分维作线性拟合，可以得到粘粒含量与分维d的关系表(表1)和散点图(图3)所示，除某断层第2号样品外，其它4个样品其相关系数达到了r＝0.932。说明粘粒土含量与分形维值存在正比，体现出分形维值是表征断层碎屑粘粒含量的一个代表性参数。

表1某断层泥分形维值与细颗粒物质的关系表

分形多孔介质固有渗透率随分形维值d增加而减小已获得理论证明，d趋于3时，渗透率趋于0。由于某断层碎屑分形维值d普遍很大，自然渗透性弱。粘粒含量在控制碎屑物质导水性方面可起到关键性作用，原因是颗粒表面静电大量吸附极性水分子形成的结合水层抗拒重力作用，不易传递静水压力，不具有流动性，致使粘性土具有很好的隔水性，因此较高粘性土含量是某断层带渗透性很低的关键原因。可以认为正是由于颗粒分形维值d普遍很高，因此某断层带渗透性必然很差。

本发明以断层泥颗粒粒径为研究对象，借助分形维值d来定性评价断层带的渗透性的方法较为新颖，且操作简单，易于实际应用，为断层带渗透性评价提供了一种新的方法和思路。

以上所述具体实例，对本发明的目的，过程和有益效果进行详细说明，并不用于限定本发明的限定范围，凡在本发明的精神原则之内，所做的任何修改、等同替换等，均应包含在本发明的保护范围之内。