一种基于张量字典约束的动态PET图像重建方法与流程

本发明属于pet成像
技术领域：
，具体涉及一种基于张量字典约束的动态pet图像重建方法。
背景技术：
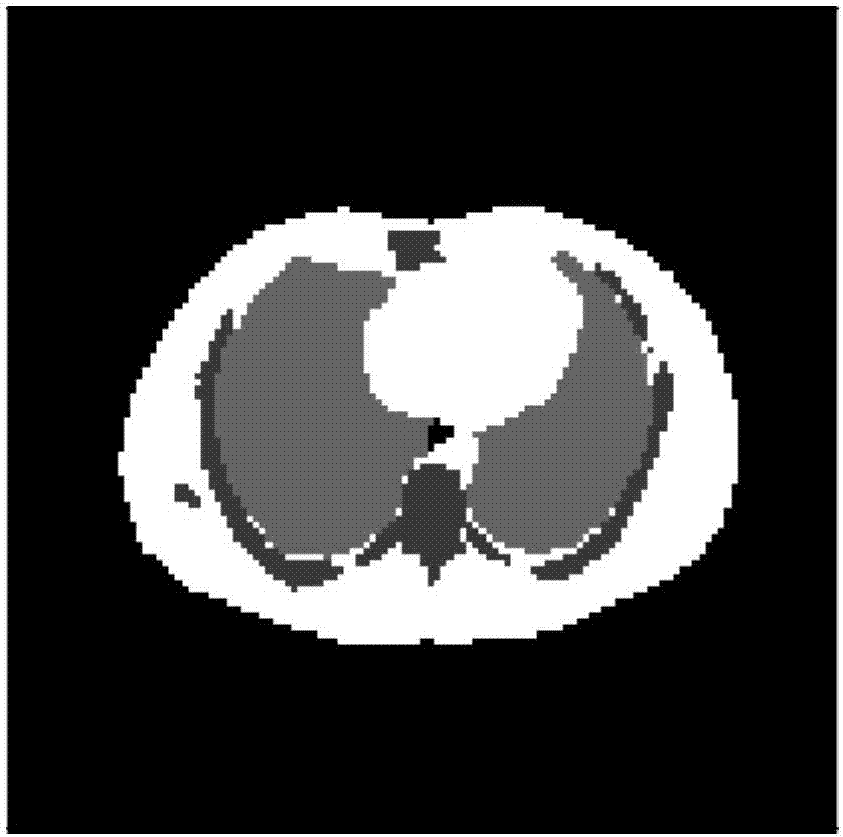
：正电子发射断层成像(positronemissiontomography，pet)是一种基于核物理学、分子生物学的医学影像技术，它能够从分子水平上观察细胞的代谢活动，为早期疾病的检测和预防提供了有效依据。动态pet是通过对患者进行一段时间的扫描，获得许多帧随时间变化的数据，这是一种功能医学显像模式，它可以记录精确的活体药代动力学定量信息，为早期癌症探测及治疗反应评估提供有效帮助。传统的动态pet重建方法是将动态数据的每一帧分别进行静态重建，从而获得重建后放射性浓度随时间变化的图像集。pet图像具有高灵敏度、高特异性的优点，但由于放射性核素受人体组织的影响会发生严重的衰减，且校正衰减的方法复杂、成本高，因此由测量得到的数据重建后的图像分辨率较低，图像略模糊。传统上，放射性浓度分布重建往往采用统计迭代方法，由于迭代法基于统计学模型，对不完全数据适应性好，逐渐成为pet重建算法研究关注点，其中包括著名的ml-em(最大似然期望最大化)、map(最大后验)和sage(惩罚似然)算法，然而这些方法只考虑了每帧数据的空间信息，忽视了每一帧数据之间的时间联系。故如何获得更精确、清晰的重建图像是本领域研究的热点。技术实现要素：鉴于上述，本发明提出了一种基于张量字典约束的动态pet图像重建方法，能够获得高质量的动态pet重建图像。一种基于张量字典约束的动态pet图像重建方法，包括如下步骤：(1)在一定时间内利用探测器对注入有放射性药剂的生物组织进行探测，采集得到对应各个时刻的符合计数向量，并建立三阶张量符合计数矩阵(2)使动态的pet图像序列组合成三阶张量pet浓度分布矩阵并根据pet成像原理建立pet测量方程；(3)通过对pet测量方程引入张量字典约束的稀疏惩罚项得到基于张量字典约束的pet图像重建模型如下：其中：为三阶张量系统矩阵，其维度为ni×nj×m；三阶张量系统矩阵中的第一层切片为ni×nj维的系统矩阵g(该矩阵表达了各像素点处出射的光子被各探测器接收到的概率)，其余m-1层切片均为ni×nj维的全零矩阵，ni为符合计数向量的维度，nj为pet浓度分布向量的维度即pet图像的像素点个数，m为采样时刻个数；λ1和λ2均为权重系数，为三阶张量pet浓度分布矩阵重新排列后的三维pet图像数据，其维度为p×m×r，p和r均为自然数且p×r＝nj；为三维pet图像数据中的第s个张量块，es为对应第s个张量块的分割算子，s为自然数且1≤s≤ns，ns为三维pet图像数据中的分块个数；为结构字典(其为利用k-svd算法从ct图像中获取的矩阵，参考文献：k-svdanalgorithmfordesigningovercompletedictionariesforsparserepresentation)，为对应第s个张量块的稀疏系数矩阵；(4)对上述pet图像重建模型进行最优化求解得到三阶张量pet浓度分布矩阵进而将其转换为动态的pet图像序列。所述三阶张量符合计数矩阵由各符合计数向量按时序排列组成，其维度为ni×1×m；所述三阶张量pet浓度分布矩阵由各时刻对应的pet浓度分布向量(即一帧pet图像)按时序排列组成，其维度为nj×1×m。所述pet测量方程的表达式如下：其中：noise为三阶张量测量噪声矩阵。所述步骤(4)中采用基于增广拉格朗日的交替方向乘子算法(alternatingdirectionmethodofmultipliers，admm)对pet图像重建模型进行最优化求解。所述交替方向乘子算法基于以下迭代方程：其中：fs和hs为辅助变量矩阵，和分别为第k+1次迭代和第k次迭代的三阶张量pet浓度分布矩阵和分别为第k+1次迭代和第k次迭代的稀疏系数矩阵和分别为第k+1次迭代和第k次迭代的三维pet图像数据和分别为三维pet图像数据和中的第s个张量块，为第k+1次迭代的结构字典和分别为第k+1次迭代和第k次迭代的辅助变量矩阵hs，为第k+1次迭代的辅助变量矩阵fs，β为惩罚系数，t表示矩阵转置，表示矩阵的摩尔-彭若斯广义逆。本发明通过引入三阶张量的概念和相关的张量乘积的定义来帮助动态pet图像重建，通过建立重建问题的张量数学模型，加入张量字典约束，基于张量字典的约束来进行动态pet图像重建；最后采取admm算法进行优化求解。故本发明有效利用张量字典约束，改善了计算机在进行pet图像重建的过程中产生的结果低分辨率和噪声干扰的问题。附图说明图1为本发明pet图像重建方法的流程示意图。图2(a)为关于肺部体模的真值图像。图2(b)为采用ml-em算法重建肺部体模的pet图像。图2(c)为采用本发明方法重建肺部体模的pet图像。具体实施方式为了更为具体地描述本发明，下面结合附图及具体实施方式对本发明的技术方案进行详细说明。如图1所示，本发明基于张量字典约束的动态pet图像重建方法，包括如下步骤；正电子发射断层扫描仪探测人体内发出的放射性信号，经过符合和采集系统处理，形成原始数据，并以正弦图的方式存放于计算机硬盘中；对原始采集到的sinogram，以已知的系统矩阵为输入项，调用相关模块。s1.根据pet探测的原理和张量定义建立重建问题的基本张量模型；s2.引入张量字典对重建进行约束；s3.初始化，设置权重系数λ1、λ2，设置初始值，s4.从设置的初始值开始，按照admm算法对目标方程求解。首先在目标方程中引入辅助变量和h；定义我们采取固定其余变量解一个变量的方式进行迭代循环求解，分别求出s5.判断是否满足迭代停止条件不满足该条件则执行步骤s4，满足则迭代停止，进而得到pet浓度分布向量实现pet成像。以下为对张量的介绍和张量矩阵乘积的相关定义：张量代表多维数据，它的阶数由数据的维度决定。如果数据则可称为三阶张量。我们将1×1×c的数据称为一个管纤维，任一三阶张量矩阵都可分解为管纤维的矩阵，而a×1×c的数据可视作管纤维的向量。我们定义是三阶张量矩阵的侧片，是三阶张量矩阵的正片，每一片都是一个a×b的矩阵。对于张量矩阵我们定义unfold函数和fold函数如下：函数的块循环矩阵的大小为ac×cb，矩阵如下：定义1：假定则张量乘积的形式可以定义为：式中张量乘积是矩阵乘法的自然延伸。定义2：给定一个管纤维集和一个侧片的线性组合，可定义：式中：乘积不成立，除非a＝1。定义3：单位张量iaac的第一个正片为a×a的单位矩阵，其余正片都为0。定义4：如果是a×b×c，则它的转置张量矩阵是b×a×c；先将每个正片进行转置，再将第2到n的正片的顺序颠倒。定义5：假定aijk是的第i，j，k项，则张量矩阵的frobenius范数为：式中：vec函数表示将张量矩阵中的数据堆叠成一个长为a×b×c的矢量，在matlab中，同时还有以下定义：完成张量的定义后，我们构建目标方程过程如下：根据张量定义，构建一个测量数据的三阶张量矩阵如下它包含了m帧正弦图矩阵转化后的列向量。与之相对应的重建图像数据它包含了m帧大小为p×r的图像，nj＝p×r。两者关系如下：式中的系统张量矩阵的第一正片为pet扫描仪的系统矩阵其余的m-1个正片均为0。考虑到图像重建解的病态问题，我们构建一个字典和它的稀疏系数用字典和稀疏表达来解决这个问题。我们用es算子从重新排列后的图像数据p×r＝nj中提取出一个三阶张量块可以将这个张量块表达成字典和其系数的乘积，字典是由q张二维大小为sp×sr数据图块组成的基，是和字典相对应的系数。基于上述条件，我们可以构建如下目标方程：式中：λ1、λ2是权重参数。基于上述目标方程，其利用admm算法的解如下：在上式中我们引入辅助变量和h，目标方程变为：由于式中有多个变量，我们采取固定其余变量解一个变量的方式进行迭代循环求解。对于解字典和其系数的子问题为：式中，k表示稀疏程度，它代表了系数中非零项的数目，可以直接通过以下公式解出：式中，代表矩阵的摩尔－彭若斯广义逆，固定后我们可以用fista算法更新每一张量块对应的对于解f的子问题为：这个最小二乘问题的解为：对于子问题为：这个问题可以用可分离抛物面替代方法解得：以下我们采用肺部数字体模模型数据实验来验证本发明的有效性，实验运行环境为：16g内存，3.40ghz，64位操作系统，cpu为inteli7。将本发明基于张量字典约束的动态pet图像重建方法和传统的ml-em方法重建结果做比较，二者使用相同的观测值y以保证结果的可比性，具体参数设置如下：y为128×128×18维采集到的sinogram。从图2可以直观地看出基于本发明重建的图像与ml-em的结果相比，ml-em算法的效果并不理想，重建图像过于平滑导致边缘十分不清晰。对比之下，采用本发明算法重建后的图片各区域有清晰地边界，且图像内部平滑。对于相同的数据，分别采用本发明和传统ml-em方法进行比较，如表1所示；应用本发明重建结果在与真值的偏差，方差均小于传统的ml-em方法，说明对本发明技术方案在提高精确度和降低噪声方面的可行性。表1方法偏差方差ml-em0.20190.1043本发明0.12710.0845上述对实施例的描述是为便于本
技术领域：
的普通技术人员能理解和应用本发明。熟悉本领域技术的人员显然可以容易地对上述实施例做出各种修改，并把在此说明的一般原理应用到其他实施例中而不必经过创造性的劳动。因此，本发明不限于上述实施例，本领域技术人员根据本发明的揭示，对于本发明做出的改进和修改都应该在本发明的保护范围之内。当前第1页12