一种大数据环境下的多群落双向驱动协作搜索算法的制作方法

本发明涉及一种大数据环境下的多群落双向驱动协作搜索算法，属于信息数据分析与挖掘
技术领域：
。
背景技术：
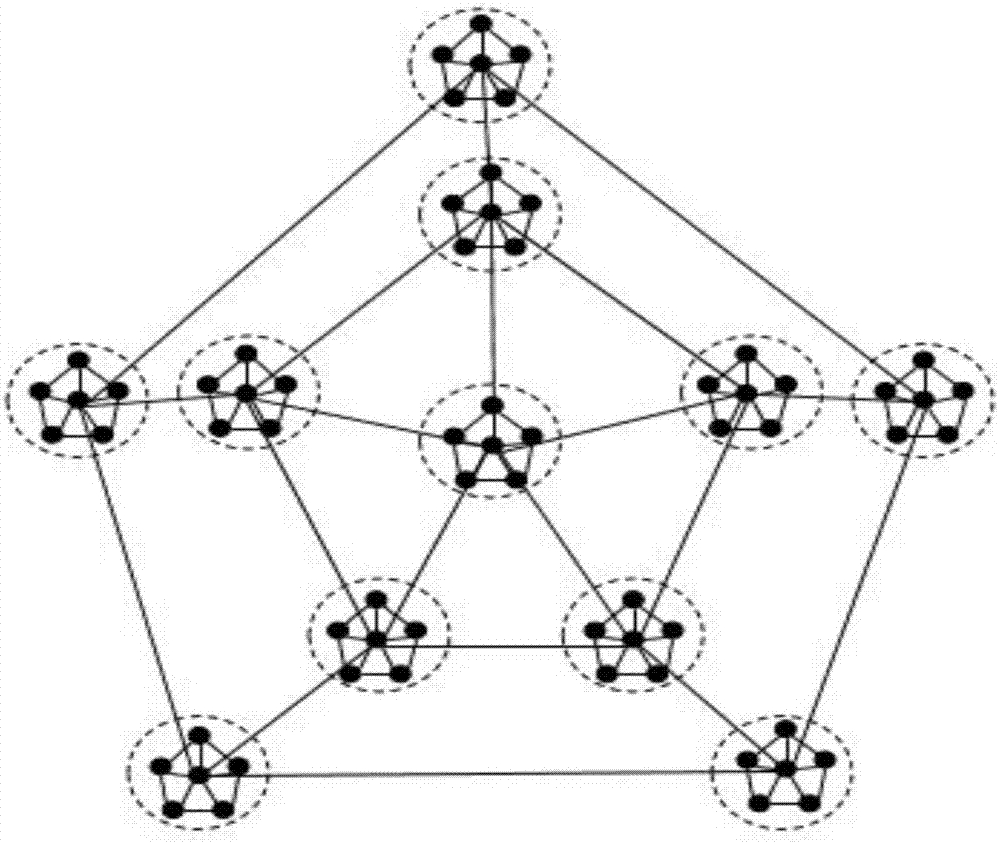
：随着互联网、移动智能终端、工业传感器、工业物联网等信息与通信技术的迅猛发展，来源于复杂工业控制系统、物联网系统，以及各种监控系统的数据呈爆炸式增长，大数据正渗透到社会生活和工业领域的方方面面，有关大数据隐藏价值挖掘的讨论也逐渐成为产业界和学术界共同关注的热点。然而，面对大数据混杂多变的特点，模型驱动方法存在本质上的局限性，很难根据先验知识建立精确模型，同时传统方法难以适应大数据分析过程中伴随的环境变化，面对大数据分析巨大的计算时空开销，可能无法在可接受的时间内得到精确解。微粒群算法是一种模拟鸟群、鱼群等生物群社会行为的群体智能算法，具有较强的自适应、自组织和泛化能力，不易受问题规模和非线性的影响，是一种解决大规模复杂优化问题的有效手段。目前，微粒群算法在进行迭代求解过程中，群体中所有微粒均以最优微粒作为目标进行追踪，群体的多样性将迅速降低，很容易陷入局部极值，出现“早熟”收敛现象，并且在进行高维粒子群优化时，优化难道较大，且优化时间过长，难以满足在大数据环境下对大规模混杂多变问题的求解需要。技术实现要素：针对上述现有技术存在的问题及不足，本发明提供了一种大数据环境下的多群落双向驱动协作搜索算法，用以解决在大数据环境下大规模混杂多变问题在求解时优化难度大、求解效率低的问题。本发明的技术方案是：一种大数据环境下的多群落双向驱动协作搜索算法，所述方法具体步骤如下：步骤1：初始化群落微粒个体p，赋予其随机的位置x和速度v；设定群落个数q，群落成员内微粒迭代次数，微粒加速常数c1、c2及惯性权重ω；步骤2：依据设定的群落个数q，将初始化的微粒个体平均分配到q个进程中，形成大小为的群落，对于取整后剩余的微粒个体随机分配到q个进程中，同时根据目标函数计算q个群落中每个微粒个体的适应值；步骤3：将q个群落分别运行于q个进程中执行异步并行进化运算：步骤3.1：设置最优位置存储区；其中最优位置存储区用于存储群落间的最优位置；步骤3.2：计算群落i的全局最优适应值fi(i＝1,2,...,q)，并依据判定阈值ft将所有群落划分为模范群落mc和普通群落cc，进而构建多群落协作网络；步骤3.3：计算群落i的节点强度si(i＝1,2,..,q)，并依据si对相应类别群落的最优位置进行评价，得到所属类中最大节点强度si对应的群落最优位置作为该所属类别群落间的最优位置，并保存到最优位置存储区；步骤3.4：各微粒群落依据双向驱动协同进化机制进行迭代进化，具体包括：规则1：群落内进化规则：每个群落内部的微粒个体均依据基本微粒群迭代公式进行进化，并产生群落的最优位置，其中普通群落的群落最优位置记作gbest，模范群落的群落最优位置记作gbest；规则2：群落间双向驱动协同进化规则：规则2.1：存在且则普通群落成员cch进入模范群落，原模范群落中末位群落mcj被舍弃；同时，将模范学习因子引入普通群落内部进化规则：其中，r1表示模范群落与普通群落间的协作关系，r表示协作关系集合，表示普通群落最优位置集合中的最优值，表示模范群落最优位置集合中的最差值，u表示普通群落的总个数，n表示模范群落的总个数，m代表的是普通群落中微粒个体的数量且m≤p，d代表最高维度，表示第t次迭代下微粒个体k在维度为d时的速度，ω表示惯性权重，c1、c2表示微粒加速常数，rand1、rand2表示[0，1]之间的随机数，c3是一个随机数且满足c1rand1+c2rand2+c3∈[0,4]，表示第t次迭代下微粒个体k在维度为d时的个体最优位置，表示第t次迭代下群落在维度为d时的最优位置，表示第t次迭代下微粒个体k在维度为d时的位置，表示第t次迭代下普通群落在维度为d时的模范学习因子；规则2.2：存在群落节点强度对任意均满足得到模范群落间最优位置：其中，r2表示模范群落与模范群落间的协作关系，表示模范群落a的群落节点强度，表示模范群落b的群落节点强度，是模范群落a的群落最优位置，将其作为模范群落间最优位置；规则2.3：存在群落节点强度对任意均满足得到普通群落间最优位置：其中，r3普通群落与普通群落间的协作关系，表示普通群落e的群落节点强度，表示普通群落f的群落节点强度，是普通群落e的群落最优位置，将其作为普通群落间最优位置；其中，群落间双向驱动协同进化规则比群落内进化规则的执行优先级更高；步骤3.5：重复执行步骤3.3～步骤3.4，并从最优位置存储区中获得全局最优解，直到达到迭代次数。所述如果fi≥ft，则表明该群落具有较强的局部寻优能力，将其作为模范群落，记作mc；如果fi<ft，则表明则该群落具有较强的全局探索能力，将其作为普通群落，记作cc。所述其中：ωio为群落ci与co之间的协作权重，ei为群落的响应度，ui为群落ci的邻域，邻域表示与群落ci存在协作关系的群落的集合。本发明的有益效果是：1.本发明在分析微粒群落特性的基础上，提出一种多群落协作搜索方法，通过协同进化机制降低群落内与群落间进化的耦合度，由节点强度表征群落间的协作强度，并采用协同规则触发对多群落协作搜索过程，可提高算法的可扩展性和自适应性，有效解决大数据混杂多变情况的优化问题；2.采用并行实施机制，设置最优位置存储区，完成各搜索进程的异步迭代，并将每一步迭代结果以广播的形式发送给其他进程，减少进程通信，提升算法的优化效率，有效降低大数据分析中巨大的计算时空开销。附图说明图1是本发明方法的流程示意图；图2是多群落协作网络示意图；图3是多群落双向驱动协同进化机制示意图；图4是rastrigin函数仿真实验图；图5是rosenbrock函数仿真实验图；图6是schaffer函数仿真实验图；图7是greiwank函数仿真实验图。具体实施方式实施例1：一种大数据环境下的多群落双向驱动协作搜索算法，选择rastrigin、rosenbrock、schaffer、greiwank四类高维复杂多模benchmark函数，对多群落双向驱动协作搜索算法进行测试分析。四个测试函数形式，f1：rastrigin函数，f2：rosenbrock函数，f3：schaffer函数，f4：greiwank函数；函数主要特征如表1所示。表1benchmark测试函数函数搜索范围初始化空间全局最优解f1(-5.1,5.1)(0,5)0f2(-100,100)(10,50)0f3(-100,100)(10,50)-1f4(-600,600)(50,300)0(1)rastrigin函数：rastrigin函数是一个典型的具有大量局部最优点的复杂多模函数，函数峰形呈现出高低起伏不定性跳跃状态，且最优值的数目随函数维数呈指数增加，该函数通常用来评价算法的适应性能。(2)rosenbrock函数：rosenbrock是一非凸病态函数，它的全局最优点位于一个平滑、狭长、难以辨别搜索方向的抛物形山谷内，此函数通常用来评价算法的执行效率。(3)schaffer函数：schaffer函数的全局最优点位于一个狭窄区域内，且距离全局最优值(3.14)的范围内存在无限多的局部最优点，函数强烈震荡的特性使其很难收敛于全局最优。(4)greiwank函数：greiwank函数是具有广泛搜索空间的典型非线性多模态函数，大量局部最优点使其成为多数优化算法难以处理的复杂多模态问题。上述4个函数，随着维数的增加，这些函数的寻优问题会变得愈发复杂，可有效评估本发明提出算法的优化性能。所述方法的具体步骤如下：步骤1：初始化群落微粒个体p，赋予其随机的位置x和速度v；设定群落个数q，群落成员内微粒迭代次数，微粒加速系数c1、c2及惯性系数ω；本实施例中，微粒个体数为4000，开启4个并行线程，微粒迭代次数为500，惯性权重ω＝1.1，微粒加速常数c1＝c2＝2。步骤2：依据设定的群落个数q，将初始化的微粒个体平均分配到q个进程中，形成大小为的群落，对于取整后剩余的微粒个体随机分配到q个进程中，同时根据目标函数计算q个群落中每个微粒个体的适应值；步骤3：将q个群落分别运行于q个进程中执行异步并行进化运算：步骤3.1：设置最优位置存储区；其中最优位置存储区用于存储群落间的最优位置；步骤3.2：计算群落i的全局最优适应值fi(i＝1,2,...,q)，并依据判定阈值ft将所有群落划分为模范群落mc和普通群落cc，进而构建多群落协作网络；所述如果fi≥ft，则表明该群落具有较强的局部寻优能力，将其作为模范群落，记作mc；如果fi<ft，则表明则该群落具有较强的全局探索能力，将其作为普通群落，记作cc。步骤3.3：计算群落i的节点强度si(i＝1,2,..,q)，并依据si对相应类别群落的最优位置进行评价，得到所属类中最大节点强度si对应的群落最优位置作为该所属类别群落间的最优位置，并保存到最优位置存储区；所述其中：ωio为群落ci与co之间的协作权重，ei为群落的响应度，ui为群落ci的邻域，邻域表示与群落ci存在协作关系的群落的集合。步骤3.4：各微粒群落依据双向驱动协同进化机制进行迭代进化，具体包括：规则1：群落内进化规则：每个群落内部的微粒个体均依据基本微粒群迭代公式进行进化，并产生群落的最优位置，其中普通群落的群落最优位置记作gbest，模范群落的群落最优位置记作gbest；规则2：群落间双向驱动协同进化规则，如图3所示，为了表示方便，图中用i、j描述；规则2.1：存在且则普通群落成员cch进入模范群落，原模范群落中末位群落mcj被舍弃；同时，将模范学习因子引入普通群落内部进化规则：其中，r1表示模范群落与普通群落间的协作关系，r表示协作关系集合，表示普通群落最优位置集合中的最优值，表示模范群落最优位置集合中的最差值，u表示普通群落的总个数，n表示模范群落的总个数，h、j分别表示任意普通、模范群落成员，m代表的是普通群落中微粒个体的数量且m≤p，d代表最高维度，表示第t次迭代下微粒个体k在维度为d时的速度，ω表示惯性权重，c1、c2表示微粒加速常数，rand1、rand2表示[0，1]之间的随机数，c3是一个随机数且满足c1rand1+c2rand2+c3∈[0,4]，表示第t次迭代下微粒个体k在维度为d时的个体最优位置，表示第t次迭代下群落在维度为d时的最优位置，表示第t次迭代下微粒个体k在维度为d时的位置，表示第t次迭代下普通群落在维度为d时的模范学习因子；规则2.2：存在群落节点强度对任意均满足得到模范群落间最优位置：其中，r2表示模范群落与模范群落间的协作关系，a、b表示任意模范群落成员，表示模范群落a的群落节点强度，表示模范群落b的群落节点强度，是模范群落a的群落最优位置，将其作为模范群落间最优位置；规则2.3：存在群落节点强度对任意均满足得到普通群落间最优位置：其中，r3普通群落与普通群落间的协作关系，e、f表示任意普通群落成员，表示普通群落e的群落节点强度，表示普通群落f的群落节点强度，是普通群落e的群落最优位置，将其作为普通群落间最优位置；其中，群落间双向驱动协同进化规则比群落内进化规则的执行优先级更高；步骤3.5：重复执行步骤3.3～步骤3.4，并从最优位置存储区中获得全局最优解，直到达到迭代次数。测试实验结果：按照上述步骤，分别对4个测试函数进行仿真实验，记录算法寻优过程的实验结果，如表2所示。表2测试结果函数进化代数最优值最差值平均值f150002.34e-0091.87e-012f2500000f3500-1-1-1f450004.03e-0082.11e-010从表2可以看出，本发明提出的多群落双向驱动协作搜索算法对于4种测试函数均表现出较强的适应能力、较快的收敛速度和较高的收敛精度；能够根据寻优过程中多种群协作规则自适应调整算法探索和搜索能力，较好的适应rastrigin峰形变化；能够根据多种群协作关系的重组，较快发现rosenbrock函数的正确搜索方向，尤其对于多模态greiwank函数，在未知峰值点个数的情况下，能够根据协作规则扩展普通种群探索能力，提高模范种群的群落节点的强度，尽可能多的搜索到峰值点。四类benchmark函数的仿真寻优过程如图4-7所示(横坐标：进化代数；纵坐标：适应度值)，可以看出，本发明的多群落双向驱动协作搜索算法能够根据寻优环境的变化，重组协同进化规则来协调不同群落间的进化搜索，不断增强普通群落的探索能力，提高模范群落的节点强度，保障群落整体的竞争力，使算法能够适应测试函数复杂多变的特性，迅速跳出局部最优点，且以较快的收敛速度，持续、有效的搜索全局最优点，可有效解决大数据复杂多变的优化问题并进一步降低巨大的计算时空开销，提高优化效率。上述过程中：多群落协作网络：一般地，假设有多个微粒群落，每个群落均是以全局最优微粒为核心的单群落寻优模式，由于多群落相互间存在进化信息交互和关联关系，使得这些微粒群落之间形成不同层次的搜索任务协作关系，这些新的任务协作关系将多个群落连接成新的网络，将之称为多群落协作网络，记作mccn。协作关系单元：设不同群落间的的协同搜索活动为一个二元组(cr)，其中c＝{c1,c2,...,cq}为参与协同搜索活动的群落序列，r:c×c为搜索过程中群落之间的交互依赖关系。称作协作关系单元，其中r1表示模范群落与普通群落间的协作关系，r2表示模范群落与模范群落间的协作关系，r3普通群落与普通群落间的协作关系。协作关系集中不同群落间协作关系单元的个数称作该协作关系集的模，记作||r||，r表示协作关系集合，r1、r2、r3组成r；协作权重：设为多群落协作网络中不同群落之间的协作权重，其中，ci与co之间的协作权重也称为多群落协作网的边权重；距离向量：将群落i的群落最优位置分别与该群落内的u个微粒的个体最优位置求差并取绝对值，得到该群落最优位置的距离向量：hi＝(h1,h2,…,hu)；响应度：设定合格距离阈值dd，依据响应值evi公式：对距离向量hi进行遍历运算，可得到该群落微粒对群落最优位置的响应值，将响应值按序相加得到该群落最优位置的响应度ei。群落节点强度：在mccn中，定义群落节点的强度为si，则其中：ωio为群落ci与co之间的协作权重，ei为群落节点的响应度，ui为群落ci的邻域，邻域表示与群落ci存在协作关系的群落的集合上面结合附图对本发明的具体实施方式作了详细说明，但是本发明并不限于上述实施方式，在本领域普通技术人员所具备的知识范围内，还可以在不脱离本发明宗旨的前提下作出各种变化。当前第1页12