基于泊松分布的二级库存最优保险储备量计算方法与流程

本发明涉及电力二级库存计算方法
技术领域：
，尤其涉及一种基于泊松分布的二级库存最优保险储备量计算方法。
背景技术：
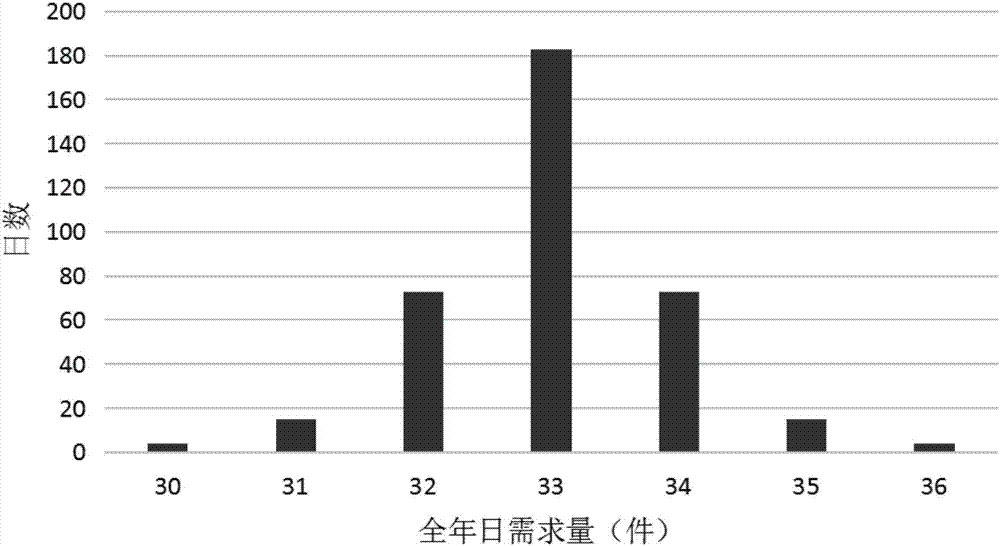
：在电力企业生产中，物资是指电力生产、建设过程中所消耗的各种生产资料。电力企业的物资储备管理是保障电力企业科学发展的重要前提，在电力企业的发展中占据了重要位置，也发挥了重要作用。以电力企业检修用的物资为例，物资储备管理的目的是在企业出现计划内的设备检修和计划外的设备检修时，能够利用已有的物资将维修、检修等工作的时间缩短，提高供电质量和供电效率，从而使电力企业能更好地进行供电服务，同时提高电力企业的经济效益。近年来，电力企业致力于提高采购、仓储、供应三者整体的运营效率，建立了“集中储备、统一配送”的供应保障新机制，基本建成了以中心库为主体、各周转库为支撑的主动配送体系。在实际工作中，特殊情况下的物资储备会形成一些无效储备，增加了管理工作的负担，降低了管理工作的效率，并在一定程度上减少了企业的可流动资金，增加了企业的运行风险。例如，电力企业物资被从存库领用后，会在一段时间内堆放在项目实施现场、供电所仓库、备品备件库等场所，形成一类小型出库物资，一般称之为“二级库”。如何提升这类小型出库物资的储备水平，优化物资储备清单及定额编制工作，为电力日常生产运行提供物力支撑，避免物资储备的补仓采购不及时等问题，也是电力企业需要解决的迫切问题之一。因此，如何确定电力企业二级库的最优保险储备量也是电力企业目前的研究课题之一。技术实现要素：为了解决上述现有技术中存在的缺点和不足，本发明提供了一种能够有效帮助电力企业确定二级库存的基于泊松分布的二级库存最优保险储备量计算方法。为了实现上述技术目的，本发明提供的基于泊松分布的二级库存最优保险储备量计算方法，包括以下步骤：步骤一：获取平均交货时间和物资每日需求量，确定每次经济订货量和每年二次库采购次数；步骤二：基于泊松分布原理确定在物资交货期内需求量的概率分布情况，并计算每种保险储备量下的采购缺货期望值；步骤三：根据所述二级采购次数和所述采购缺货期望值，获取不同保险储备量下与物资缺失和保险储备相关的总成本，并从所述总成本中选取最低值作为最优保险储备量。优选的，所述获取平均交货时间以及物资每日需求量，确定每次经济订货量和每年二次库采购次数，包括：根据公式一计算储备物资总成本，其中，fwz为储备物资总成本，q1为每年物资年需求量，q2为每次需求量，f1为每次二级库订货成本，q3为每日从一级库转移至二级库的送货量，q4为每日物资耗用量，f2为与物资数量有关的年单位变动储存成本；对公式一中的每次需求量q2进行边界求导运算，结合公式二计算得到的最优值为每次经济订货量q*，其中，q*为每次经济订货量；对公式一中的每次需求量q2进行边界求导运算，结合公式二计算得到的最优值为每次经济订货量q*，其中，qcs为每年二级库从一级库采购的次数。优选的，所述步骤二包括：假设初始状态的再订货点为qd,0、保险储备量为qb,i(i＝1，2，···，n)，在不同保险储备量下再订货点转变为qd,i(i＝1，2，···，n),qd,0、qb,i、qd,i三者间的关系如公式四，qd，i＝qd,0+qb，i(i＝1，2，···，n)，公式四；记第i种保险储备量下一次采购的缺货期望值为假设平均交货时间t为定值，物资全年的平均日需求量记为qp，k(k＝1，2，···，m)，存货交货期内的需求量为qj，k(k＝1，2，···，m)，从小到大依次记为qj,1、qj,2、···、qj,m，每种物资需求量对应的概率为gk(k＝1，2，···，m)，若qj，j-1＜qd，i且qj，j≥qd，i，则建立如公式五的数学模型，且qj，k＝t×qp，k(k＝1，2，···，m)，公式六。优选的，假设所述每种物资需求量服从泊松分布原理，gk(k＝1，2，···，m)对应物资交货期期间[t，t+δt]内对物资需求量为qj，k(k＝1，2，···，m)的概率，则gk(k＝1，2，···，m)服从参数为λδt的泊松分布，满足公式七，考虑日需求量，令δt＝1并代入公式七，得到公式八，令公式八的均值和方差均为λ，根据公式九通过最大似然估计计算λ，其中，xi为二级物资日需求量的统计数据，n为统计数据xi的个数；根据公式十的似然方程，结合公式九计算λ，将公式十一代入公式八得到每种物资需求量对应的概率gk，将公式十二代入公式五运算得到第i种保险储备量下的采购缺货期望值优选的，所述步骤三包括：在第i种保险储备量下，设与物资缺失和保险储备相关的总成本为fwz，i，缺货成本为fqh，i,保险储备成本为fbx，i,则通过公式十三计算不同保险储备量下与物资缺失和保险相关的总成本fwz，i，并从总成本fwz，i中选取最低值为最优保险储备量。采用上述技术方案后，本发明提供的基于泊松分布的二级库存最优保险储备量计算方法具有如下优点：1、本发明提供的二级库存最优保险储备量计算方法，为电力企业解决了物资交货期内需求量的问题，帮助电力企业获得了每种保险储备量下一次采购的缺货期望值，有利于帮助电力企业在储备物资满足补仓要求的情况下降低购买储备物资的总成本，电力企业在物资满足二级库存使用要求的前提下减少了成本支出。有利于提高电力企业的管理工作效率，降低电力企业运行风险。2、本发明将泊松分布的统计方法引入了电力企业二级库物资储备的计算过程，大大提高了计算结果的合理性，进而保证二级库存最优保险储备量计算结果的可靠性，避免电力企业因计算结果不合理而遭受损失，降低电力企业的运行风险。3、通过本发明的计算方法，可以计算出每种不同保险储备量下物资缺失和保险相关的总成本，总成本为最低值的即为最优保险储备量，有利于帮助电力企业合理降低在物资缺失和保险相关方面的支出。附图说明图1为本发明实施例基于泊松分布的二级库存最优保险储备量计算方法的流程图；图2为某电力企业二级库物资在某年内日需求量的统计直方图。具体实施方式如图1所示，本发明实施例提供的基于泊松分布的二级库存最优保险储备量计算方法，包括以下步骤：步骤一：获取平均交货时间和物资每日需求量，确定每次经济订货量和每年二次库采购次数；步骤二：基于泊松分布原理确定在物资交货期内需求量的概率分布情况，并计算每种保险储备量下的采购缺货期望值；步骤三：根据所述二级采购次数和所述采购缺货期望值，获取不同保险储备量下与物资缺失和保险储备相关的总成本，并从所述总成本中选取最低值作为最优保险储备量。步骤一的具体计算过程为：根据公式一计算储备物资总成本，其中，fwz为储备物资总成本，q1为每年物资年需求量，q2为每次需求量，f1为每次二级库订货成本，q3为每日从一级库转移至二级库的送货量，q4为每日物资耗用量，f2为与物资数量有关的年单位变动储存成本；对公式一中的每次需求量q2进行边界求导运算，结合公式二计算得到的最优值为每次经济订货量q*，其中，q*为每次经济订货量；根据每年物资年需求量q1和每次经济订货量q*计算每年二级库从一级库采购的次数qcs,其中，qcs为每年二级库从一级库采购的次数。步骤二包括的具体计算过程为：假设初始状态的再订货点为qd,0、保险储备量为qb，i(i＝1，2，···，n)，在不同保险储备量下再订货点转变为qd，i(i＝1，2，···，n),qd,0、qb，i、qd，i三者间的关系如公式四，qd，i＝qd,0+qb，i(i＝1，2，···，n)，公式四；记第i种保险储备量下的采购缺货期望值为假设平均交货时间t为定值，物资全年的平均日需求量记为qp，k(k＝1，2，···，m)，存货交货期内的需求量为qj，k(k＝1，2，···，m)，从小到大依次记为qj,1、qj,2、···、qj,m，每种物资需求量对应的概率为gk(k＝1，2，···，m)，若qj，j-1＜qd，i且qj，j≥qd，i，则建立如公式五的数学模型，且qj，k＝t×qp，k(k＝1，2，···，m)，公式六；假设每种物资需求量服从泊松分布原理，gk(k＝1，2，···，m)对应物资交货期期间[t，t+δt]内对物资需求量为qj，k(k＝1，2，···，m)的概率，则gk(k＝1，2，···，m)服从参数为λδt的泊松分布，即考虑日需求量，令δt＝1并代入公式七，得到公式八，令公式八的均值和方差均为λ，根据公式九通过最大似然估计计算λ，其中，xi为二级物资日需求量的统计数据，n为统计数据xi的个数；根据公式十的似然方程，结合公式九计算λ，将公式十一代入公式八得到每种需求量的概率gk，将公式十二代入公式五运算得到第i种保险储备量下的采购缺货期望值步骤三的具体计算过程为：在第i种保险储备量下，设与物资缺失和保险储备相关的总成本为fwz，i，缺货成本为fqh，i,保险储备成本为fbx，i,则通过公式十三计算不同保险储备量下与物资缺失和保险相关的总成本fwz，i并选取最低值为最优保险储备量。为了更好的说明本实施例基于泊松分布的二级库存最优保险储备量计算方法，下面结合具体数据进一步说明。如图1的所示，假设某电力企业二级库物资在某年内日需求量的统计直方图如图2所示，本实施例计算方法的模型相关参数如表1所示，保险储备量设置情况如表2所示。表1、模型相关参数设置表参数描述(单位)数值qb,0初始状态的保险储备量(件)0qb,1第1种保险储备量(件)5qb,2第2种保险储备量(件)10qb,3第3种保险储备量(件)15表2、保险储备量设置情况在不同保险储备量下，根据公式四，结合表1、表2中的参数数据得到相应的再订货点，如表3所示。参数描述(单位)数值qd,1第1种保险储备量情况(件)170qd,2第2种保险储备量情况(件)175qd,3第3种保险储备量情况(件)180表3、不同保险储备量下的再订货点根据图2可知二级库物资全年平均日需求量的概率分布情况，如表4所示。表4、二级库物资全年平均日需求量的概率分布情况根据公式六，结合表1、表4计算二级库物资交货期内的需要量，如表5所示。表5、二级库物资交货期内的需要量及概率分布情况根据公式五，结合表3、表5计算不同保险储备量情况下的采购缺货期望值，如表6所示。表6、不同保险储备量情况下的采购缺货期望值根据公式十三，结合表1、表2和表6计算每种保险储备量下与物资缺失和保险储备相关的总成本，如表7所示。表7、每种保险储备量下与物资缺失和保险储备相关的总成本根据表7可知，在第三种保险储备量情况下，当保险储备量为10件时，与物资缺失和保险储备相关的总成本为398元，为三种保险储备量情况下的最低值，因此，确定10件为二级库存的最优保险储备量。除上述优选实施例外，本发明还有其他的实施方式，本领域技术人员可以根据本发明作出各种改变和变形，只要不脱离本发明的精神，均应属于本发明权利要求书中所定义的范围。当前第1页12