基于统计分析的电力用户高可靠性供电计算系统的制作方法

本发明涉及电力数据分析，具体涉及基于统计分析的电力用户高可靠性供电计算系统。

背景技术：

高可靠性供电费用，是为了保障重要用户连续不间断用电，而允许用户占用更多的电网资源，因此对其征收的费用。根据国家电网营销〔2010〕1247号关于印发《国家电网公司业扩报装工作规范(试行)》和《国家电网公司业扩供电方案编制导则》的通知，根据对供电可靠性的要求以及中断供电危害程度，重要电力客户可以分为特级、一级、二级重要电力客户和临时性重要电力客户。在符合《国家电网公司业扩供电方案编制导则》规定且具备供电条件的情况下，用户选择多路供电是否合算成为了许多用户关心的热点。

技术实现要素：

本发明所要解决的技术问题就是提供一种基于统计分析的电力用户高可靠性供电计算系统，对电力用户高可靠性供电的成本进行计算。

为解决上述技术问题，本发明采用如下技术方案：基于统计分析的电力用户高可靠性供电计算系统，包括：

输入模块，输入用户停电的历史数据；

停电预测模块，根据用户停电的历史数据计算用户停电次数的概率分布情况，并预测用户停电时间；

第一成本计算模块，根据停电预测模块的输出结果计算用户全额支付高可靠性费用，但不承担停电损失的成本总额；

第二成本计算模块，根据停电预测模块的输出结果计算用户支付部分高可靠性费用，但需承担一定停电损失的情况下的成本总额；

第三成本计算模块，根据停电预测模块的输出结果计算用户全额承担停电风险情况下的成本总额；

成本比较模块，比较第一成本计算模块、第二成本计算模块、第三成本计算模块的输出的成本总额；

输出模块，根据成本比较模块的比较结果输出成本总额最小的成本计算模块。

进一步的，停电预测模块的计算方法包括如下子步骤：

1.1假设用户停电次数服从泊松分布，基于用户停电次数的历史数据，对参数进行估计，

首先假设用户停电次数服从泊松分布，

记p{x＝k,δt}为在时间段[t,t+δt]内发生k次停电的概率，则p{x＝k,δt}服从参数为λδt的泊松分布，即：

考虑单位时间内的停电次数，令δt＝1，则：

该分布的均值和方差均为λ，

根据极大似然估计方法估算参数λ，

首先求似然函数为

其中，xi为年停电次数的历史数据，n为历史观测数据xi的个数，

似然方程为

得解

其中λ^*为极大似然估计量，由于泊松分布的均值即λ，因此用户停电次数的期望为

1.2计算预计用户停电总时长，

假设用户平均每次停电的时间为h，则预计每年用户停电总时长为

进一步的，第一成本计算模块的计算方法包括如下子步骤：

3.1计算全额支付的高可靠性费用，

当为自建本级电压外部供电工程时，

当vc＝10kv时，f＝160×ca

当vc＝35kv时，f＝9×ca(9)

当非自建本级电压外部供电工程时，

当vc＝10kv时，f＝220×ca

当vc＝35kv时，f＝170×ca(10)

当电压不等于10kv且不等于35kv时，

f＝90×ca(11)

其中，vc为电压等级，f为上交供电公司的高可靠性费用，最小备用容量为ca；3.2计算全额支付高可靠性费用情境下的全周期总成本，

电力用户为享受高可靠性服务，首先需要投资建设部分设备及网架，这部分投资用in1表示，

则电力用户为享受高可靠性服务，共需花费的成本tc'1为

tc'1＝in1+f(12)；

3.3计算全额支付高可靠性费用情境下的年均成本，

tc1＝tc'1·(a,p,i,m)(13)

其中，tc1为年均成本，i为折现率，m为一次性支付成本后可享受高可靠性服务的总时间。

进一步的，第二成本计算模块的计算方法包括如下子步骤：

4.1计算用户愿意承担的一定风险概率下的停电损失，

假设用户自身可以承受的停电时间在预计停电总时长中的占比为α。则承担的停电损失总额为

l2＝h·α·lh(14)

其中，lh为每小时停电损失估算值；

4.2计算与风险程度对应的用户高可靠性费用总额，

tc'2＝in2+f·α(15)

其中，tc'2为电力用户与风险程度对应的全周期高可靠性费用，用户投资费用为in2；

4.3计算用户支付部分高可靠性费用，但需承担一定停电损失的情况下的成本年值，

tc2＝tc'2·(a,p,i,m)+l2(16)

其中tc2为部分停电风险自留情境下的年均成本。

进一步的，第二成本计算模块的计算方法包括如下子步骤：

4.1计算用户愿意承担的一定风险概率下的停电损失，

假设用户自身可以承受的停电时间在预计停电总时长中的占比为α，则承担的停电损失总额为

l2＝h·α·lh(14)

其中，lh为每小时停电损失估算值；

4.2计算与风险程度对应的用户高可靠性费用总额，

tc'2＝in2+f·α(15)

其中，tc'2为电力用户与风险程度对应的全周期高可靠性费用，用户投资费用为in2。

4.3计算用户支付部分高可靠性费用，但需承担一定停电损失的情况下的成本年值。

tc2＝tc'2·(a,p,i,m)+l2(16)

其中tc2为部分停电风险自留情境下的年均成本。

进一步的，第三成本计算模块计算用户全额承担停电风险情况下的成本总额

tc3＝h·lh，lh为每小时停电损失估算值。

本发明采用的技术方案，使用统计分析的方法，预测电力用户停电的期望时长，从而计算可能产生的停电损失。将电力用户可选择的高可靠性投资方案分为三种：全额交付高可靠性供电费用，从而保证自身用电最高限度的可靠性，发生的停电损失由供电公司全额赔付；只交付部分的高可靠性费用，但需要承受一定范围内的停电损失；不交付高可靠性费用，停电损失完全由用户自身承担。比较不同方案下电力用户需要支付的总成本，帮助选择其中成本较小的高可靠性供电投资方案。

与现有技术相比，本发明具有以下优点和有益效果：

(1)本发明提出的方法基于数据分析，对电力用户高可靠性供电的成本进行计算，为电力用户解决高可靠性供电投资的决策问题提供了依据，帮助用户节约用电成本。

(2)本发明将统计分析的方法引入电力用户高可靠性供电计算系统，从而提高分析结果的可靠性。

附图说明

下面结合附图和具体实施方式对本发明作进一步描述：

图1为本发明的具体流程图；

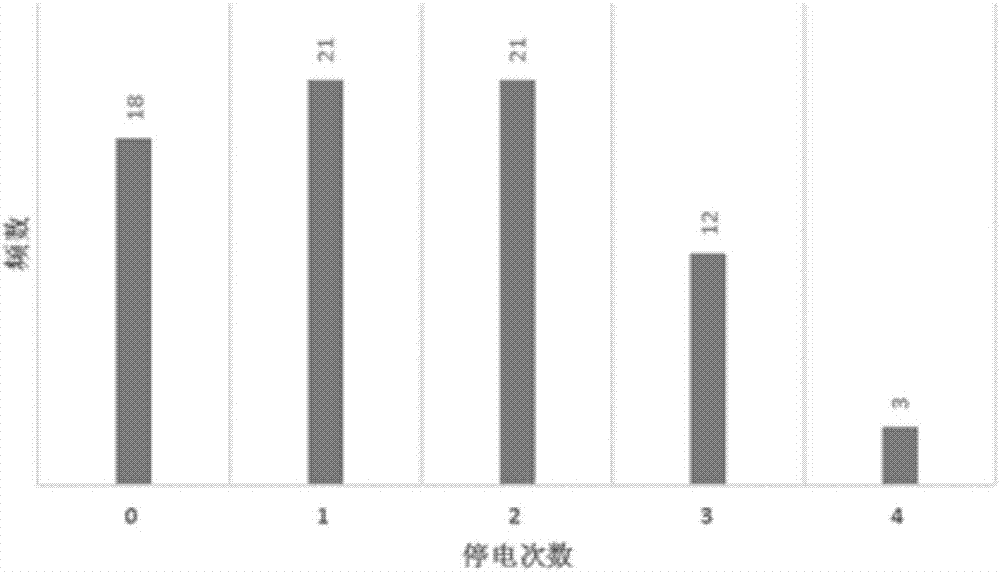
图2某用户的停电次数统计直方图。

具体实施方式

下面结合本发明实施例的附图对本发明实施例的技术方案进行解释和说明，但下述实施例仅为本发明的优选实施例，并非全部。基于实施方式中的实施例，本领域技术人员在没有做出创造性劳动的前提下所获得其他实施例，都属于本发明的保护范围。

基于统计分析的电力用户高可靠性供电计算系统，包括

输入模块，输入用户停电的历史数据；

停电预测模块，根据用户停电的历史数据计算用户停电次数的概率分布情况，并预测用户停电时间；

第一成本计算模块，根据停电预测模块的输出结果计算用户全额支付高可靠性费用，但不承担停电损失的成本总额；

第二成本计算模块，根据停电预测模块的输出结果计算用户支付部分高可靠性费用，但需承担一定停电损失的情况下的成本总额；

第三成本计算模块，根据停电预测模块的输出结果计算用户全额承担停电风险情况下的成本总额；

成本比较模块，比较第一成本计算模块、第二成本计算模块、第三成本计算模块的输出的成本总额；

输出模块，根据成本比较模块的比较结果输出成本总额最小的成本计算模块。

本发明使用统计分析的方法，预测电力用户停电的期望时长，从而计算可能产生的停电损失。将电力用户可选择的高可靠性投资方案分为三种：全额交付高可靠性供电费用，从而保证自身用电最高限度的可靠性，发生的停电损失由供电公司全额赔付；只交付部分的高可靠性费用，但需要承受一定范围内的停电损失；不交付高可靠性费用，停电损失完全由用户自身承担。比较不同方案下电力用户需要支付的总成本，帮助选择其中成本较小的高可靠性供电投资方案。

下面结合附图进一步说明本发明的具体实施方式。

见图1，

停电预测模块的计算方法进一步包括如下子步骤：

1.1假设用户停电次数服从泊松分布，基于用户停电次数的历史数据，对参数进行估计。

相关文献指出，电网系统故障次数近似服从泊松分布，系统故障将会引起用户停电，因此首先假设用户停电次数服从泊松分布。

记p{x＝k,δt}为在时间段[t,t+δt]内发生k次停电的概率，则p{x＝k,δt}服从参数为λδt的泊松分布，即：

考虑单位时间内的停电次数，令δt＝1，则：

该分布的均值和方差均为λ。

根据极大似然估计方法估算参数λ。

首先求似然函数为

其中，xi为年停电次数的历史数据，n为历史观测数据xi的个数。

似然方程为

得解

其中λ^*为极大似然估计量。由于泊松分布的均值即λ，因此用户停电次数的期望为

1.2计算预计用户停电总时长。

假设用户平均每次停电的时间为h，则预计每年用户停电总时长为

步骤2进一步包括子步骤：

2.1计算全额支付的高可靠性费用。

当为自建本级电压外部供电工程时，

当vc＝10kv时，f＝160×ca

当vc＝35kv时，f＝9×ca(9)

当非自建本级电压外部供电工程时，

当vc＝10kv时，f＝220×ca

当vc＝35kv时，f＝170×ca(10)

当电压不等于10kv且不等于35kv时，

f＝90×ca(11)

其中，vc为电压等级，f为上交供电公司的高可靠性费用，最小备用容量为ca。上述高可靠性费用单位：元/kva。

2.2计算全额支付高可靠性费用情境下的全周期总成本。

电力用户为享受高可靠性服务，首先需要投资建设部分设备及网架，这部分投资用in1表示。

则电力用户为享受高可靠性服务，共需花费的成本tc'1为

tc'1＝in1+f(12)

2.3计算全额支付高可靠性费用情境下的年均成本。

tc1＝tc'1·(a,p,i,m)(13)

其中，tc1与

tc1为年均成本，i为折现率，m为一次性支付成本后可享受高可靠性服务的总时间。

等额分付现值公式

等额分付现值指，在考虑资金时间价值的条件下，若折现率为i，假设m年内每年现金流均为a，则相当于在第1年年初的现金流为p，p的计算公式为

上式可简记为(p,a,i,m)

等额分付资本回收公式

等额分付资本回收公式是等额分付现值公式的逆运算，即已知现值，求与之等价的等额年值。

上式可简记为(a,p,i,m)

(p,a,i,m)的计算方法为现有技术，在此不再赘述。

第三成本计算模块计算用户全额承担停电风险情况下的成本总额进一步包括子步骤：

3.1计算用户愿意承担的一定风险概率下的停电损失。

假设用户自身可以承受的停电时间在预计停电总时长中的占比为α。则承担的停电损失总额为

l2＝h·α·lh(14)

其中，lh为每小时停电损失估算值。

3.2计算与风险程度对应的用户高可靠性费用总额。

tc'2＝in2+f·α(15)

其中，tc'2为电力用户与风险程度对应的全周期高可靠性费用，用户投资费用为in2。

3.3计算用户支付部分高可靠性费用，但需承担一定停电损失的情况下的成本年值。

tc2＝tc'2·(a,p,i,m)+l2(16)

其中tc2为部分停电风险自留情境下的年均成本。

步骤4：第三成本计算模块计算用户全额承担停电风险情况下的成本总额

tc3＝h·lh(17)

步骤5：比较tc1、tc2、tc3，选择其中成本最小的方案作为结果输出。

需要说明的是，上述计算公式中出现的“点”表示乘号，另外除了用户停电的历史数据外，引入的其他外部数值如，h、ca、α、in1、in2、l2、lh等直接输入即可。

下面将结合应用实例进一步说明本发明。

假设某用户的停电次数统计直方图如图2所示。

模型相关参数如表1所示。

表1参数设置表

根据上述参数，结合步骤1～5中的相关公式，计算可得三种情境下用户需要付出的年成本总额如表2所示。

表2成本计算结果表

由上表可以推算，当用户全额交付高可靠性费用时，年均成本最低，因此用户可以选择这种投资方案。

以上所述，仅为本发明的具体实施方式，但本发明的保护范围并不局限于此，熟悉该本领域的技术人员应该明白本发明包括但不限于附图和上面具体实施方式中描述的内容。任何不偏离本发明的功能和结构原理的修改都将包括在权利要求书的范围中。