电网资产保险支出测算模型的制作方法

本发明涉及电力技术。
背景技术：
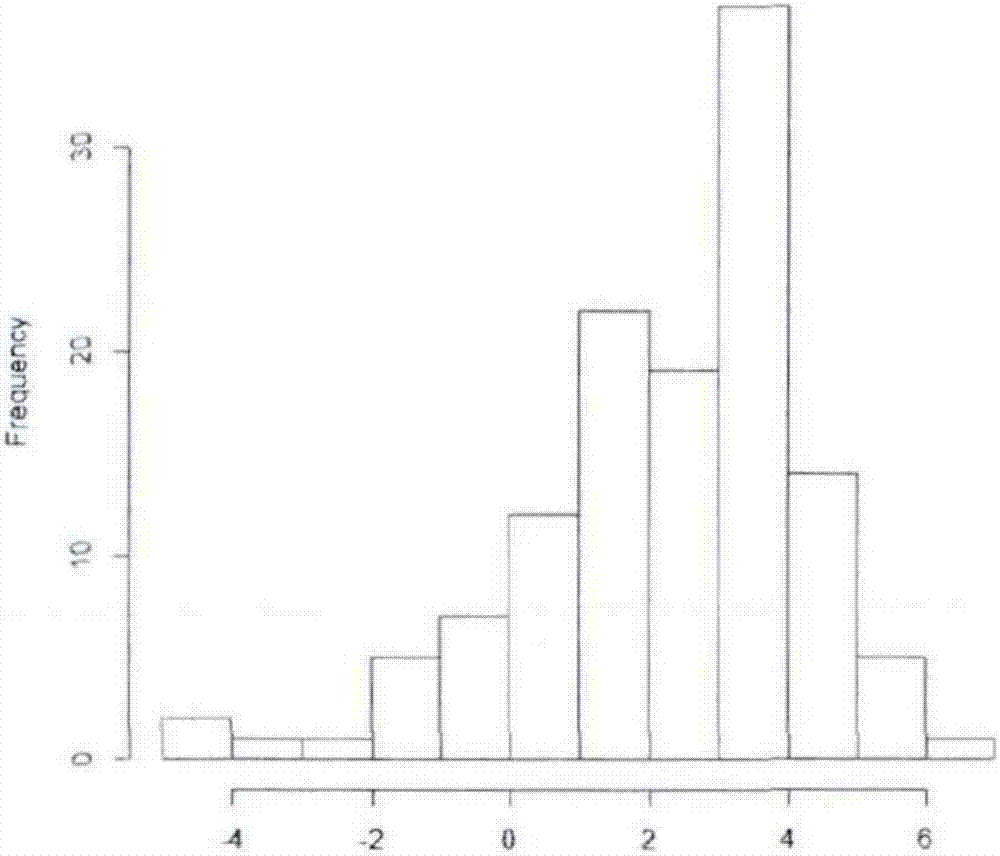
：电力企业是较为典型的资产密集型企业，固定资产数量大，种类多，分布广，对资产从竣工投产、设备运营、更新改造，到其毁损报废的一系列管理工作是电力公司经营管理业务的重要构成。在这个资产全寿命周期管理工作中，对资产开展保险管理工作是其中的一个重要部分，也是落实资产精益化管理的要求。如2008年冰冻灾害、2013年余姚水灾等导致电网设备大规模损毁，给电网企业经营带来了较大的冲击。增强资产保险意识，树立全局观念，维护电力企业资产权益，是电力企业经营管理者需要具有的一种战略思想。为了更好的开展资产保险管理工作，需要对电网资产的保险费用进行合理评估，测算保险费用合理性。技术实现要素：本发明所要解决的技术问题就是提供一种电网资产保险支出测算模型，基于电网资产发生严重水灾造成的损失数额及损失次数的历史数据，测算电网企业的合理保险支出。为解决上述技术问题，本发明采用如下技术方案：电网资产保险支出测算模型，包括：输入模块，输入电网资产发生严重灾害造成的损失数额及损失次数的灾害损失样本数据；灾害损失预测模块，根据电网资产发生严重灾害造成的灾害损失样本数据，基于gpd分布的pot模型测算电网资产在发生严重灾害时可能产生的损失；灾害次数预测模块，根据电网资产发生严重灾害造成的灾害损失样本数据，基于泊松分布测算电网资产每年可能发生严重灾害的次数；灾害损失总额测算模块，根据发生严重灾害时可能产生的损失与每年可能发生严重灾害的次数，测算电网资产每年由于严重灾害可能产生的损失总额；输出模块，输出灾害损失总额测算模块测算出的损失总额。进一步的，灾害损失预测模块的测算方法包括如下子步骤：1.1灾害损失样本数据修正修正公式如下：其中，i为样本数据的编号，n为样本数据的个数，xi为修正后的样本数据，xi为修正前的样本数据，p为预测年的物价水平，c为预测年的资产规模，pi为样本数据所处年份的物价水平，ci为样本数据所处年份的资产规模；1.2构建灾害损失基于gpd分布的pot模型设x1,x2,…xn是一个独立同分布的随机变量，具有相同的累积分布函数f(x)＝p{xi＜x}，对某一足够大的临界值u，存在一个正的函数β(u)，则超出量yi＝xi-u的分布近似表示为当ξ≥0时，y≥0，ξ＜0时，则称x服从gpd分布，根据ξ的取值将gpd分布进一步分为三种形式：由于yi的分布为条件超额分布，即：即1.3选取阈值运用r软件中ismev程序包中的mrl.plot函数绘出台风巨灾损失数据的平均超出量函数图，选择其中存在正线性相关关系的区间，作为阈值的初选范围，使用r软件下ismev包中的gpd.fitrange函数绘得在初选范围内的各待选阈值对应的形状参数和尺度参数估计量，选择稳定范围内的最大值作为最后的阈值选择结果。进一步的，灾害次数预测模块的测算方法为：假设电网资产由于严重灾害导致损失超过阈值u的次数服从泊松分布，记p{k＝k,δt}为在时间段[t,t+δt]内发生k次损失超过阈值的严重灾害的概率，则p{k＝k,δt}服从参数为λδt的泊松分布，即：考虑单位时间内的停电次数，令δt＝1，则：该分布的均值和方差均为λ，根据极大似然估计方法估算参数λ，首先求似然函数为其中，ki为年停电次数的历史数据，n为历史观测数据ki的个数，似然方程为得解∵∴其中λ*为极大似然估计量，由于泊松分布的均值即λ，因此用户停电次数的期望为进一步的，灾害损失预测模块的测算方法包括如下子步骤：3.1计算年损失总额的期望值年损失总额表示为其中，k表示导致损失额超过阈值的重大灾害次数，xi表示第i次损失额超过阈值时的损失额度，相应的均值和方差公式如下：e(s)＝e[e(s|k)]＝e(n)·e(x)var(s)＝var[e(s|k)]+e[var(s|k)]＝var[k·e(x)]+e[k·var(x)]＝e2(x)·var(k)+e(k)·var(x)以表示服从形状参数为ξ、尺度参数为β、阈值为u的gpd分布的均值，则：3.2计算var值var值是在险价值，令n为样本数，n0为大于阈值u的样本的数量，则(n-n0)/n近似表示f(u)，f(x)表示为尾部估计表示为对于给定的置信水平q，3.3计算cvar值cvar值指损失大于某个特定的var值的条件下，该投资组合损失的平均值，本发明采用的技术方案，利用广义帕累托分布对电网资产在严重灾害下可能产生的损失进行预测，并对可能发生严重损失的频数进行概率统计，测算电网资产由于严重灾害可能产生的损失总额。基于测算的损失额度，合理确定电网资产的保险支出。与现有技术相比，本发明具有以下优点和有益效果：(1)本发明提出的方法为测算电网企业的合理保险支出提供了依据，帮助企业合理调配资金，从而保证电网企业的经济运行。(2)本发明将统计分析的方法引入测算电网企业的合理保险支出问题，从而提高分析结果的可靠性。附图说明下面结合附图和具体实施方式对本发明作进一步描述：图1为本发明的具体流程图；图2为水灾损失分布直方图；图3为重大水灾频次直方图。具体实施方式下面结合本发明实施例的附图对本发明实施例的技术方案进行解释和说明，但下述实施例仅为本发明的优选实施例，并非全部。基于实施方式中的实施例，本领域技术人员在没有做出创造性劳动的前提下所获得其他实施例，都属于本发明的保护范围。电网资产保险支出测算模型，包括：输入模块，输入电网资产发生严重灾害造成的损失数额及损失次数的灾害损失样本数据；灾害损失预测模块，根据电网资产发生严重灾害造成的灾害损失样本数据，基于gpd分布的pot模型测算电网资产在发生严重灾害时可能产生的损失；灾害次数预测模块，根据电网资产发生严重灾害造成的灾害损失样本数据，基于泊松分布测算电网资产每年可能发生严重灾害的次数；灾害损失总额测算模块，根据发生严重灾害时可能产生的损失与每年可能发生严重灾害的次数，测算电网资产每年由于严重灾害可能产生的损失总额；输出模块，输出灾害损失总额测算模块测算出的损失总额。本发明以水灾为例，利用广义帕累托分布对电网资产在严重水灾下可能产生的损失进行预测，并对可能发生严重损失的频数进行概率统计，测算电网资产由于严重水灾可能产生的损失总额。基于测算的损失额度，合理确定电网资产的保险支出。下面结合附图进一步说明本发明的具体实施方式。灾害损失预测模块的测算方法包括如下子步骤：1.1水灾损失样本数据修正由于选取的电网资产水灾损失数据与企业资产规模及物价水平相关，因此需要将获取的历史损失样本数据基于预测年的物价水平及资产规模进行修正，修正公式如下：其中，i为样本数据的编号，n为样本数据的个数，xi为修正后的样本数据，xi为修正前的样本数据，p为预测年的物价水平，c为预测年的资产规模，pi为样本数据所处年份的物价水平，ci为样本数据所处年份的资产规模。1.2构建水灾损失基于gpd分布的pot模型关于极端天气与自然灾害等的研究指出，巨灾风险并不符合正态分布特征，而通常以属于极值分布的gpd分布来对其进行具体地拟合预测。gpd分布以过程为单位进行数据收集，样本数据为所统计过程的最大值，即极值。一般情形下发生极值事件的概率极小，但一旦发生则损失巨大，严重水灾损失即属于极值事件。设x1,x2,…xn是一个独立同分布的随机变量，具有相同的累积分布函数f(x)＝p{xi＜x}，对某一足够大的临界值u，存在一个正的函数β(u)，则超出量yi＝xi-u的分布可近似表示为当ξ≥0时，y≥0，ξ＜0时，则称x服从gpd分布。根据ξ的取值又可将gpd分布进一步分为三种形式：由于yi的分布为条件超额分布，即：即1.3选取阈值运用r软件中ismev程序包中的mrl.plot函数绘出台风巨灾损失数据的平均超出量函数图，选择其中存在正线性相关关系的区间，作为阈值的初选范围。采用参数估计值稳定法确定阈值u：如果相应的超出量服从gpd分布，则对于大于初始值阈值u0的其他阈值u，相应的形状参数和尺度参数估计量应该保持一致。在此基础上，还应该选择尽量大的阀值。使用r软件下ismev包中的gpd.fitrange函数绘得在初选范围内的各待选阈值对应的形状参数和尺度参数估计量，选择稳定范围内的最大值作为最后的阈值选择结果。再运用r软件中gpd.fit函数得gpd分布的参数u,β,ξ的估计结果。在计算得到相应的参数后，可使用广义帕累托分布与超出分布拟合图、分布尾部拟合图和模型残差的q-q图来判断拟合的优度。国内外众多学者通过实证数据验证了台风、地震等自然灾害发生严重损失的频数可以通过泊松分布进行拟合。灾害次数预测模块的测算方法为，假设电网资产由于严重水灾导致损失超过阈值u的次数服从泊松分布。记p{k＝k,δt}为在时间段[t,t+δt]内发生k次损失超过阈值的严重水灾的概率，则p{k＝k,δt}服从参数为λδt的泊松分布，即：考虑单位时间内的停电次数，令δt＝1，则：该分布的均值和方差均为λ。根据极大似然估计方法估算参数λ。首先求似然函数为其中，ki为年停电次数的历史数据，n为历史观测数据ki的个数。似然方程为得解∵∴其中λ*为极大似然估计量。由于泊松分布的均值即λ，因此用户停电次数的期望为灾害损失预测模块的测算方法包括如下子步骤：3.1计算年损失总额的期望值年损失总额可以表示为其中，k表示导致损失额超过阈值的重大水灾次数，xi表示第i次损失额超过阈值时的损失额度。相应的均值和方差公式如下：e(s)＝e[e(s|k)]＝e(n)·e(x)(15)var(s)＝var[e(s|k)]+e[var(s|k)]＝var[k·e(x)]+e[k·var(x)]＝e2(x)·var(k)+e(k)·var(x)(16)以表示服从形状参数为ξ、尺度参数为β、阈值为u的gpd分布的均值，则：3.2计算var值var值是在险价值，即在一般市场状态下，在一定置信水平下，一定期间内的某一金融工具或投资组合可能面临的最大潜在损失值。令n为样本数，n0为大于阈值u的样本的数量，则(n-n0)/n可以近似表示f(u)，f(x)可表示为尾部估计可以表示为对于给定的置信水平q，3.3计算cvar值cvar值指损失大于某个特定的var值的条件下，该投资组合损失的平均值，又称为期望损失。对于给定的置信水平q，有把握认为重大水灾损失年度总额不会超过需要说明的是，上述计算公式中引入的数据直接从数据库调取即可。下面将结合应用实例进一步说明本发明。假设某地区水灾损失分布情况如图2所示。该分布属于gpd分布，根据步骤1所述，利用r软件计算该分布的阈值u及相关参数，计算结果如表1所示。表1gpd分布参数计算结果表参数数值u3.63β0.6929ξ-0.0692对每年内损失额超过阈值的次数进行统计，统计结果如图3所示。根据极大似然估计，泊松分布参数估计结果为1.48。根据步骤3，置信水平设为95％，var与cvar值的估计结果如表2所示。表2var、cvar估计结果表参数数值var122cvar215即有95％的把握可以认为最大损失为215亿元。以上所述，仅为本发明的具体实施方式，但本发明的保护范围并不局限于此，熟悉该本领域的技术人员应该明白本发明包括但不限于附图和上面具体实施方式中描述的内容。任何不偏离本发明的功能和结构原理的修改都将包括在权利要求书的范围中。当前第1页12