一种非线性系统的状态估计方法与流程

本申请属于航空航天、智能交通、模式识别以及医学工程
技术领域：
，具体地说，涉及一种非线性系统的状态估计方法。
背景技术：
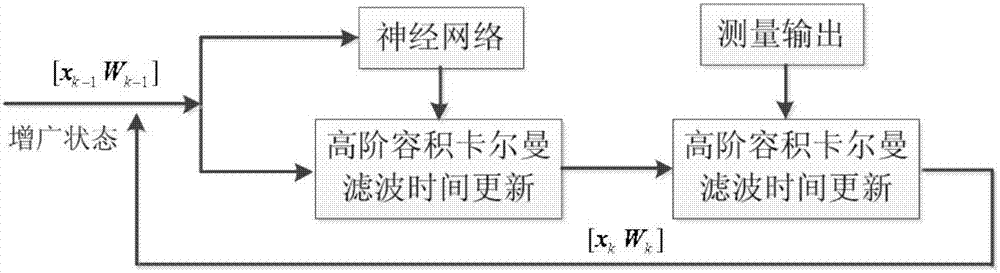
：非线性系统状态模型未知情况下，现有的基于非线性滤波和神经网络的算法对非线性系统状态估计的精度受限。当系统模型未知时，采用神经网络对模型进行非线性近似是一种简单而有效的方法。神经网络根据实际数据集确定网络逼近的非线性函数，然而，当实际系统的状态变量不完全可测时，单独采用神经网络将无法建立过程的模型。状态空间模型法对系统的内部状态和外部可观测输出变量之间的变化关系进行描述，由于该方法可以对系统内部复杂的状态进行估计和预测，因此已经被广泛的应用在动态系统的处理当中。对系统的状态空间模型建立完成之后，就需要对利用合适的方法对系统的状态进行估计。滤波方法在状态空间中利用系统输入输出观测数据，对系统状态进行最优估计。这种滤波的方法不仅可以对状态进行估计，还可以对神经网络系统参数进行辨识。非线性滤波算法在参数估计中得到了长足的发展，特别是在神经网络的参数辨识方面，其将网络的权系数参数看作特殊的状态进行估计。现有的方法利用神经网络建立状态空间模型，将网络权系数作为系统的状态变量，进而基于扩展卡尔曼滤波算法对状态变量进行实时更新。扩展卡尔曼滤波是目前应用最为广泛的一种非线性滤波方法，然而当系统的非线性程度较高，一阶近似会带来非常大的截断误差，扩展卡尔曼滤波算法的估计性能将随之大大下降，甚至发散。由于扩展卡尔曼滤波稳定性差、精度低等缺点，julier等人提出了无迹卡尔曼滤波，使用无迹变换来处理均值和方差的非线性传递。已经有不少学者利用无迹卡尔曼滤波和神经网络来解决未知系统模型的非线性系统状态估计问题。大量的仿真实验结果表明基于无迹卡尔曼滤波算法的神经网络算法明显优于基于扩展卡尔曼滤波算法的神经网络算法。然而无迹卡尔曼滤波的精度仍然有限，而且当系统维数较高时，其估计性能明显降低。技术实现要素：有鉴于此，本申请针对状态模型未知的非线性系统，提出了一种基于高阶容积卡尔曼滤波算法和神经网络的非线性系统状态估计方法，该方法利用神经网络对系统状态进行建模，并利用高阶容积卡尔曼滤波算法对状态进行实时更新估计，本发明方法弥补了现有算法的不足。一种非线性系统的状态估计方法，包括以下步骤：步骤一：将非线性系统的状态与神经网络的权系数组合起来，利用神经网络建立状态空间模型，将网络的权系数和非线性系统的状态组合一起为增广的状态变量；步骤二：采用高阶容积卡尔曼滤波算法对神经网络系统状态进行时间更新，以及根据时间更新后的结果进行测量更新，从而实现网络权系数的自适应调整和状态的实时更新。进一步地，如上所述的方法，步骤一包括：将系统的状态与神经网络的权系数组合起来，形成增广状态xa＝[xw]t，则可建立如下所示的非线性系统：其中，fj(xk)为神经网络对非线性系统建立的数学模型：g(x)为神经网络sigmod核函数，wk为神经网络的权系数，新系统的过程噪声wk和观测噪声vk均为独立的零均值高斯白噪声，并且对应的协方差矩阵分别为qk，rk；xk代表第k时刻的状态向量，代表第k时刻的增广状态向量，zk代表表示第k时刻的观测向量，代表非线性观测函数。进一步地，如上所述的方法，步骤二对状态进行时间更新包括：6)在时刻k，假设k-1时刻的误差协方差已知且为pk-1|k-1，分解因数：其中，向量sk-1|k-1为pk-1|k-1的cholesky分解；代表sk-1|k-1的转置，t代表转置操作；7)计算容积点代表第k-1时刻增广状态的估计值；其中m＝2n，向量ξi为式中，ei表示n维单位向量且其第i个元素为1；分别为8)计算状态方程传播后的容积点(i＝1，2，…，m)9)计算一步状态预测其中，权值wi分别为10)计算一步预测误差协方差矩阵进一步地，如上所述的方法，步骤二根据时间更新后的结果进行测量更新包括：10)分解因数：sk|k-1代表矩阵分解值；11)计算更新后的状态容积点12)计算测量方程传播后的容积点13)计算k时刻一步量测预测14)计算新息协方差矩阵15)计算一步预测互协方差矩阵16)计算增益矩阵17)计算更新状态18)计算协方差矩阵与现有技术相比，本申请可以获得包括以下技术效果：本发明针对未知状态模型的非线性系统，首先利用神经网络建立状态空间模型，将网络的权系数和系统的状态组合一起为增广的状态变量，然后采用高阶容积卡尔曼滤波算法对神经网络系统状态进行估计预测，从而实现网络权系数的自适应调整和状态的实时更新，提高了非线性系统状态的估计精度，仿真实验表明了本发明所提算法的有效性。附图说明此处所说明的附图用来提供对本申请的进一步理解，构成本申请的一部分，本申请的示意性实施例及其说明用于解释本申请，并不构成对本申请的不当限定。在附图中：图1是神经网络的模型结构；图2是状态估计系统原理图；图3为仿真实验中状态1的估计曲线；图4为仿真实验中状态2的估计曲线；图5为仿真实验中状态1的误差曲线；图6为仿真实验中状态2的误差曲线。具体实施方式以下将配合附图及实施例来详细说明本申请的实施方式，藉此对本申请如何应用技术手段来解决技术问题并达成技术功效的实现过程能充分理解并据以实施。神经网络的状态空间模型神经网络的结构模型一般可分为前馈神经网络模型、反馈神经网络模型以及随机神经网络模型等。目前在各个行业领域中前馈神经网络模型应用最为广泛，其状态空间的模型结构如图1所示，其中，x1,x2,...xn用来表示输入的样本节点，y1,y2,...ym用来表示输出样本节点，θ1,θ2,...θq表示权重系数，该神经网络模型结构共有三个节点层，分别为输入层、隐层和输出层，各个层之间通过权系数进行连接，输入输出层在两端，中间隐含层的节点数根据实际要求进行选取。高阶容积卡尔曼滤波原理首先考虑如下离散非线性系统：xk＝f(xk-1)+wk(1)zk＝h(xk)+vk(2)其中，xk为n维的状态向量；zk为m维的观测向量；函数f，h为已知的非线性函数；{wk}与{vk}均为独立的零均值高斯白噪声。对于一般的非线性系统，在高斯假设下可将贝叶斯估计基本理论与任意阶容积规则相结合，从而推导出高阶的容积卡尔曼滤波。与无迹卡尔曼滤波结构相同，同样分为状态预测(时间更新)和测量更新两个步骤，主要是高阶容积卡尔曼滤波采用的是相径容积规则解决了高维系统维数爆炸问题。高阶容积规则满足：式中，ej为n维空间rn的单位矢量矩阵的第j列。与为如下式所示的点集：权系数和分别为其中，是单位球面的表面积，根据矩匹配法，当n＝2时，权值为：基于高阶容积卡尔曼滤波和神经网络的状态估计当系统的模型未知时，采用神经网络对系统模型进行建模逼近，那么就需要求解最优的网络节点权系数，同时状态也是未知的，然而，状态跟权系数是彼此联系的，因此，本发明将系统的状态和权系数组合在一起作为新的状态，将原来的系统方程和权系数方程的增广方程作为新的系统模型，进而利用高阶容积卡尔曼滤波算法对状态和权系数实时估计，具体的系统原理如图2所示。图2当中，在k-1时刻，原系统的状态xk-1与权系数wk-1组合成新的增广状态向量[xk-1wk-1]，输入到神经网络中，进而高阶容积卡尔曼滤波根据增广状态和神经网络的输出结果进行时间更新步骤，最后高阶容积卡尔曼滤波结合时间更新的结果和测量的输出结构进行时间更新得到k时刻的系统增广状态值[xkwk]，并作为下次系统的输入状态。具体算法如下：首先将系统的状态与神经网络的权系数组合起来，形成增广状态xa＝[xw]t，则可建立如下所示的非线性系统：其中，fj(xk)为神经网络对非线性系统建立的数学模型：g(x)为神经网络sigmod核函数，wk为神经网络的权系数，新系统的过程噪声wk和观测噪声vk均为独立的零均值高斯白噪声，并且对应的协方差矩阵分别为qk，rk。然后对状态进行时间更新：1)在时刻k，假设k-1时刻的误差协方差已知且为pk-1|k-1，分解因数：其中，向量sk-1|k-1为pk-1|k-1的cholesky分解。2)计算容积点其中m＝2n，向量ξi为式中，ei表示n维单位向量且其第i个元素为1。分别为3)计算状态方程传播后的容积点(i＝1，2，…，m)4)计算一步状态预测其中，权值wi分别为5)计算一步预测误差协方差矩阵最后进行测量更新：19)分解因数：20)计算更新后的状态容积点21)计算测量方程传播后的容积点22)计算k时刻一步量测预测23)计算新息协方差矩阵24)计算一步预测互协方差矩阵25)计算增益矩阵26)计算更新状态27)计算协方差矩阵对于公式(9)(10)所描述的已知非线性系统，给定状态初始条件p0|0，即可根据上述的时间更新和测量更新两个步骤进行高阶容积卡尔曼滤波，得到增广的状态向量值。仿真实验考虑如下非线性系统离散模型y(k)＝x1(k)+x2(k)+v(k)(30)其中，过程噪声w(k)和观测噪声v(k)均是相互独立的零均值高斯白噪声，且方差分别为和r(k)＝0.1，初始状态x0＝[100.6]t，初始状态估计值为以及初始状态误差协方差矩阵为神经网络隐层节点数为10，核函数选择sigmod型，初始权重设为方差为0.3的随机噪声，漂移方差阵为qw＝0.022i40×40。为了对比方便，本发明对如下算法进行如下简单标记：算法1：基于高阶容积卡尔曼滤波和神经网络的估计算法算法2：基于无迹卡尔曼滤波和神经网络的估计算法仿真结果如图1-图6及表1所示。表1估计误差对比平均绝对估计误差算法1算法2状态10.18350.2830状态20.22020.5663从图3和图4的估计曲线来看，算法1和算法2都能对原始状态进行较好的跟踪估计，说明两种算法都是有效的，从图4和图5的估计误差曲线来看，两种算法的误差很快趋于稳定，且算法1的误差明显要小于算法的误差，从表1的统计数据来看，算法1的状态估计精度大大高于算法2，特别是在对状态2的估计精度上，算法2的估计误差是算法1估计误差的两倍多，这主要是因为高阶容积卡尔曼滤波算法的估计精度高于无迹卡尔曼滤波算法，从而说明了基于高阶容积卡尔曼滤波和神经网络的估计算法的有效性。上述说明示出并描述了本申请的若干优选实施例，但如前所述，应当理解本申请并非局限于本发明所披露的形式，不应看作是对其他实施例的排除，而可用于各种其他组合、修改和环境，并能够在本申请构想范围内，通过上述教导或相关领域的技术或知识进行改动。而本领域人员所进行的改动和变化不脱离本申请的精神和范围，则都应在本申请所附权利要求的保护范围内。当前第1页12