一种基于增强局部搜索能力的人工蜂群优化方法与流程

本发明涉及优化领域，尤其涉及一种基于增强局部搜索能力的人工蜂群优化方法。

背景技术：

优化是许多科学和工程领域中一个重要的问题，在生产与生活中，人们经常会遇到如何安排生产资源、销售计划，或者怎样合理选取参数、路径，才能使总利润最大、总成本最小、总时间最短，或使相应产品指标达到最优、资源利用率迖到最经济等诸如此类的问题，这些问题都可以归结为最优化问题。传统的优化方法具有对初值的强依赖性、容易陷入局部极值点、可能得不到全局最优值、一般要求解析的目标函数是连续且可导的，变量也是连续的、而对于一些复杂的非线性的、离散的或多目标值的优化问题，用传统的优化方法很难得到理想的结果等缺点。为了解决这些问题，研究者们开始将目光转向对大自然中生物所展示出的智能行为的模拟和研究，从而开启了一个重要的研究领域仿生智能计算来解决以往难以实现的优化问题。

人工蜂群算法(abc)是一种模拟蜜蜂群体寻找优良蜜源的仿生智能计算方法，与遗传算法、粒子群算法、蚁群算法等智能计算方法相比，该算法的突出优点是在每次迭代中都进行全局和局部搜索、控制参数少、易于实现、计算方便等。

但是，人工蜂群算法仍存在一些问题，种群初始化盲目性、局部搜索能力弱和易陷入局部最优的缺点。因此，本发明人对其进一步的探索和研究，提出一种基于增强局部搜索能力的人工蜂群优化方法。

技术实现要素：

本发明的技术目的在于提出一种基于增强局部搜索能力的人工蜂群优化方法，以增强局部搜索能力，与abc的较强全局搜索能力平衡，提高收敛速度，改善算法性能。

为了解决上述技术问题，本发明的技术方案如下：

一种基于增强局部搜索能力的人工蜂群优化方法，包括以下步骤：

步骤1、设置esabc的参数，所述参数包括种群大小sn、采蜜蜂个数ne、跟随蜂个数no、最大迭代次数mcn、个体维数d、阈值limit；

步骤2、按公式(1)进行初始化，得到初始种群：

其中，i＝1,2,…,sn,j＝1,2,…,d；sn表示食物源(解)的数量；d表示解的维数；由公式(2)所得：

所述公式(2)为洛伦兹混沌系统，通过该公式产生三组分布均匀、遍历性好的混沌迭代序列；其中，取x(0),y(0),z(0)为初始值，δ，γ，β为洛伦兹系统的参数，取值分别为δ＝10，β＝8/3,γ＞24.74，从产生的三组混沌序列中随机选一维，记作

步骤3、根据公式(3)分别计算各个解的适应值fit，并将适应值排名前sn/2的解作为初始的采蜜蜂种群，剩余的蜜蜂则为观察蜂种群：

fiti＝0.1/(0.1+1/|lgfi|),0≤fi≤10^-λ(3)

其中，fiti表示第i个个体的适应值，fi表示第i个个体的函数值，λ则由计算机的计算精度决定；

步骤4、在由步骤3选择出来的采蜜蜂附近进行邻域搜索，搜索策略如公式(4)所示：

其中，r为{1,2,…,sn}内的随机整数，且r≠i，i和j的含义同公式(1)，为[-1,1]内的随机数，随机为第r个蜜蜂的第j维，代表当代种群中最优个体的第j维，即当前种群最优解引导下一代个体的进化方向，可以达到增强局部搜索能力和提高解精度的效果；

步骤5、按照公式(3)计算其适应值fit_new，若fit<fit_new，更新当前采蜜蜂，trial(i)＝0,否则，trial(i)++；

步骤6、对于跟随蜂，首先根据公式(5)计算选择概率p，以概率p(i)搜索新的食物源，然后转化为采蜜蜂进行邻域搜索，根据公式(3)计算适应值，比较并判断是否更新，同时修改标识向量trial(i)；其中概率计算如公式(5)所示：

步骤7、判断trial(i)>limit是否成立，若成立，则放弃该食物源，进入侦查蜂阶段，根据公式(1)生成新的食物源，若不成立，转至步骤8；

步骤8、记录最优解；

步骤9、判断是否满足终止条件iter≥mcn，若满足，则输出最优解，否则，返回步骤4。

采用上述方案后，本发明具有以下特点：

一、初始化种群时采用一种遍历性好、分布均匀的高维混沌序列产生方式，增强了初始种群的多样性和分布性，在一定程度上避免了abc中随机初始化的盲目性；

二、采用基于对数的适应度评价方式划分初始的采蜜蜂种群和观察蜂种群，通过该方法把个体间差异明显化，扩大了种群个体适应值的差异性，减小了选择压力，进而把函数值相似但不同的种群个体区分开，使得优秀个体有更大的概率被跟随开采；

三、本发明并采用一种增强局部搜索能力的搜索策略，在一定程度上有效地避免了陷入局部最优，提高了解的精度。

下面结合附图和具体实施方式对本发明的技术方案进行详细说明。

附图说明

图1是本发明一种基于增强局部搜索能力的人工蜂群优化方法的流程简图；

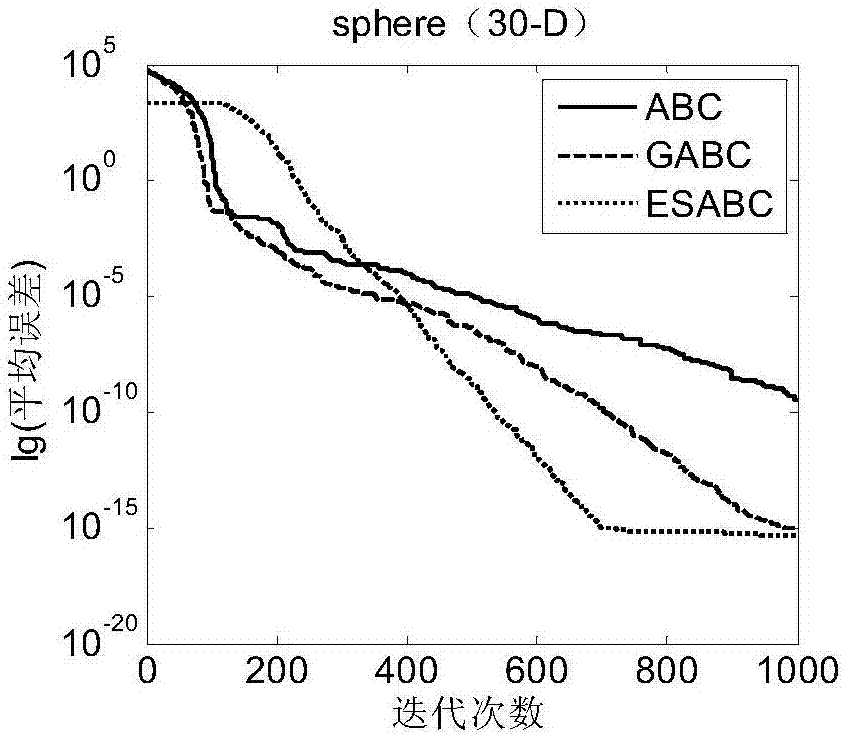
图2-12是本发明分别对于11个测试函数在d＝30的情况下的进化曲线图；

图13-22是本发明分别对于11个测试函数在d＝60的情况下的进化曲线图。

具体实施方式

本发明公开的一种基于增强局部搜索能力的人工蜂群优化方法(esabc)，能够达到搜索某一问题最优解的目的。下面是本发明的一个实施例，具体说明如何应用本发明esabc。

实施例：通过matlab(商业数学软件，用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境)对12个典型的函数最小化问题的仿真寻优来测试本发明esabc的性能，并与abc(传统人工蜂群算法)、gabc(用于与本发明esabc性能比较，参考zhug,kwongs.gbest-guidedartificialbeecolonyalgorithmfornumericalfunctionoptimization[j].appliedmathematics&computation,2010,217(7):3166-3173.)进行比较。测试函数介绍如表1所示。

表1.测试函数

表1中f01-f04为单峰函数，f05-f12为多峰函数。esabc，abc和gabc被用于优化上述函数，三个算法在相同的实验背景下运行，且每个测试函数独立运行10次以避免偶然性，并记录最优值、最差值、平均值和方差。

如图1所示，是采用本发明的一种基于增强局部搜索能力的人工蜂群优化方法对上述12个典型的函数最小化问题的仿真寻优过程，包括：

s1、设置初始参数。本例设初始参数为：维数d＝30&60，种群个数sn＝150，最大迭代次数mcn＝1000，阈值limit＝100；

s2、按公式(1)进行初始化，得到初始种群：

其中，i＝1,2,…,sn,j＝1,2,…,d；sn表示食物源(解)的数量；d表示解的维数；由公式(2)所得：

所述公式(2)为洛伦兹混沌系统，通过该公式产生三组分布均匀、遍历性好的混沌迭代序列，在一定程度上避免了abc中随机初始化的盲目性；其中，取x(0),y(0),z(0)为初始值，δ，γ，β为洛伦兹系统的参数，取值分别为δ＝10，β＝8/3,γ＞24.74，从产生的三组混沌序列中随机选一维，记作

s3、根据公式(3)分别计算各个解的适应值fit，即将步骤s2得到的初始个体向量(解)代入测试函数，即得到目标函数值fi，如ellipitic函数，目标函数值然后将fi代入公式(3)计算适应值fit，并将适应值排名前75的解作为初始的采蜜蜂种群，剩余的蜜蜂则为观察蜂种群：

fiti＝0.1/(0.1+1/|lgfi|),0≤fi≤10^-λ(3)

其中，fiti表示第i个个体的适应值，fi表示第i个个体的函数值，λ则由计算机的计算精度决定，此处，取λ＝8；

其他测试函数采用同样方式计算每个个体的适应值fit；

s4、在由步骤s3选择出来的采蜜蜂附近进行邻域搜索，搜索策略如公式(4)所示：

其中，r为{1,2,…,sn}内的随机整数，且r≠i，i和j的含义同公式(1)，为[-1,1]内的随机数，随机为第r个蜜蜂的第j维，代表当代种群中最优个体的第j维，采用该搜索策略，当前种群最优解引导下一代个体的进化方向，可以达到增强局部搜索能力和提高解精度的效果；

s5、按照公式(3)计算其适应值fit_new，若fit<fit_new，更新当前采蜜蜂，trial(i)＝0,否则，trial(i)++；

步骤6、对于跟随蜂，首先根据公式(5)计算选择概率p，以概率p(i)搜索新的食物源，然后转化为采蜜蜂进行邻域搜索，根据公式(3)计算适应值，比较并判断是否更新，同时修改标识向量trial(i)；其中概率计算如公式(5)所示：

s7、判断trial(i)>limit是否成立，若成立，则放弃该食物源，进入侦查蜂阶段，根据公式(1)生成新的食物源，若不成立，转至s8；

s8、记录最优解；

s9、判断是否满足终止条件iter≥mcn，若满足，则输出最优解，否则，返回s4。

表2和表3分别为d＝30和d＝60的实验结果，其中d＝30的情况对其中11个函数进行测试，d＝60的情况在10个函数进行测试。

表2.三种算法优化结果(d＝30)

表3.三种算法优化结果(d＝60)

由表2可看出：对于单峰函数，esabc的解的精度和稳定性均优于abc和gabc；对于多峰函数，除了himmelblau函数，esabc的性能均优于abc和gabc。

由表3可以看出：d＝60时，除了ackley函数，esabc的解均优于abc和gabc。

收敛曲线用于评价三种算法的性能。为了更好地分析收敛曲线，在迭代中取对数，三种算法的收敛曲线如图2-12(d＝30)及图13-22(d＝60)所示。由图2-12可知：对于himmelblau函数，三个算法的收敛精度一样，esabc的收敛速度比gabc慢，比abc快；对于其他函数，esabc的收敛精度均好于abc和gabc,收敛速度总体上快于另外两个算法。由图13-22可知：除了ackley函数的精度和收敛速度差于gabc，优于abc；对于其余函数，esabc的解均优于abc和gabc。

总体来说，本发明esabc在解的精度和收敛速度方面都有所提高。

以上所述，仅是本发明较佳实施例而已，并非对本发明的技术范围作任何限制，故凡是依据本发明的技术实质对以上实施例所作的任何细微修改、等同变化与修饰，均仍属于本发明技术方案的范围内。