一种基于改进朴素贝叶斯的个人收入分类方法与流程

本发明属于分类方法领域，涉及一种处理连续型数据的改进朴素贝叶斯分类方法，具体是一种基于改进朴素贝叶斯的个人收入分类方法，用于判断个人收入属于何种水平。

背景技术：

随着社会的不断发展，人们的购买力也在不断的提高，网上购物也成为了年轻人的主要购买手段。因此，一大批的购物网站应用而生，伴随着的是对于商品推荐系统的旺盛需求。

在推荐商品时，首先应该对用户的收入水平进行确认，然后根据收入对用户进行分类，再对不同类的用户推荐不同的商品。但是目前的大部分用户分类系统都是根据用户购买东西的种类和数量进行分类，这种分类方法有一定的优势，它可以根据用户的购物记录对老用户进行准确的分类，确定这些用户属于哪一类的收入水平。但是对于新注册的用户，由于没有购买记录，因此无从判断。

本发明基于这一现状，提出了一种基于改进朴素贝叶斯的个人收入判断分类方法。

分类是用于数据挖掘、机器学习和模式识别等方面的一个关键步骤。它属于有监督学习，主要过程是通过对数据集进行分析，从而得到数据集中蕴含的分类原理，进而建立分类器，然后依靠分类器来确定未分类的数据所属的类别。

朴素贝叶斯分类算法是基于贝叶斯定理实现的。贝叶斯定理是在条件概率已知的情况下，可以得到两个事件交换后的概率。而朴素贝叶斯算法就是基于这种原理发展出来的，对于给出的待分类项，求解在此项出现的条件下，属于各个类别时分别出现的概率，哪个最大，就认为此待分类项属于哪个类别。但是，由于贝叶斯定理的条件独立特性和所有属性对结果影响程度相同的问题，在朴素贝叶斯算法实际使用时，其准确度偏低，所以很多人据此对朴素贝叶斯算法做出了改进。

目前对朴素贝叶斯算法的改进方法主要有：第一种，利用频繁项集的针对文本数据的结合apriori算法改进朴素贝叶斯分类器，这种方法分类效果极佳，但是使用范围较窄，只适用于文本数据；第二种，针对属性对结果影响的结合属性加权的朴素贝叶斯分类器，这种方法可以在一定程度上提高分类的准确率，但是在单独使用的情况下仍然无法得到优秀的效果；第三种，针对算法的基本公式进行改进，这种方法在提高准确率的同时不会造成其他的后果，但是改进面较窄，不利于之后的进一步研究。

技术实现要素：

本发明的目的针对上述问题，提出一种基于关联规则的改进贝叶斯分类方法，并将其应用于个人收入判断分类方法中。这种方法是基于关联规则来提升准确率的，可以适用于除文本数据以外的其他种类的数据集，解决了关联规则改进的贝叶斯算法只适应于文本分类的问题。在本方法中首先提出了基于连续型数据的类条件概率估计方法，用于确定各类的类条件概率。其次，在分割后的数据集中引入拉普拉斯校准，避免0点影响过大的问题。再次，提出一种改进关联规则算法，这种方法可以根据训练集的分类结果来衡量两个属性之间的密切关系。最后，引入属性加权的概念，从而解决朴素贝叶斯算法所有属性对结果影响相同的问题。

为实现上述技术问题，本发明所采用的技术解决方案如下：一种基于连续型数据集的改进朴素贝叶斯算法，包括以下步骤：

步骤(1)、获取用于甄别居民收入水平的数据集，其中属性变量包括年龄、工种、学历、性别、工作地点等用于对居民收入水平进行分类的信息；

上述收集的数据集属性变量包括连续型属性和离散型属性；

步骤(2)、对步骤(1)获取的数据集中离散文字型属性进行量化处理：

从离散文字型属性中选择一个属性，将其中文字相同的元素用相同的数字表示，文字内容不同的元素不得使用同一数字表示。

譬如选择工种属性，在工种属性中包括医生，教师，律师等文字内容，量化处理过程为，将工种属性中出现的所有内容为医生的元素用1来代替，教师用2来代替，律师用3来代替，不得出现教师，律师皆用1来代替的情况。

步骤(3)、对步骤(1)获取的数据集中连续型属性进行离散化处理：

3.1从数据集中选择连续型属性a；

3.2根据数据集中存在的分类结果c1，c2，…，cn，将属性a中分属不同类别的元素集合记为ac1，ac2，…，acn。

3.3计算ac1，ac2，…，acn均值μ1，μ2，…，μn和方差

3.4采用高斯公式计算相邻两个类别元素集aci和ac(i+1)的交点xi，记为q1，q2，…，qn-1。交点的计算公式如下：

其中1≤i≤n-1；

3.5将交点q1，q2，…，qn-1按从小到大的顺序进行排列，并以其为分割点对属性a的所有元素进行分类，构成元素集a1，a2，…，an。

3.6将3.5处理后的同属一类的所有元素用一个常数来代替，属于不同类别的则必须使用不同的常数来代替(比如a1中的用数字1来代替，a2中的用2来代替…；a1和a2不能同使用数字1来代替)。

3.7采用步骤3.1-3.6对其他的连续型属性进行离散化处理，直到所有的连续属性皆处理完毕，整理归并；

步骤(4)、对步骤(2)-(3)初步处理后对数据集中存在的类条件概率为0的情况进行处理；

类条件概率是以类别作为条件的概率。在步骤4中具体指在某属性类别中，某总分类结果出现的概率。举个例子，即在医生这一属性类别中，年收入超过50w的医生占全部医生的概率。反过来说也属于类条件概率，但是不便于理解。

通过使用拉布拉斯校准来避免0点影响过大的问题，故在每一属性的类条件概率对应的属性数量值上加1，从而避免0的出现；

步骤(5)、求出各属性各类的先验概率和类条件概率p(ai|cj),其中ai表示属性a中第i个属性类别，cj表示分类结果c中第j个类别。

步骤(6)、采用改进的关联规则算法来判断属性之间的相关性，判断出关联度较高的属性：

6.1选择属性类别个数相同的属性，判断同一总分类结果ck下任意两个属性类别的关联程度：

p(ai|ck)-p(bi|ck)，i≤n，k≤n；

属性类别是指属性自己内部的类别，比如我们上文提到的工种属性中的医生，律师，教师等分类。

若所有关联程度绝对值均小于0.2，则说明在总分类结果ck中，属性a和b的相关度较高，故需要继续判断其他总分类结果中属性a和b的相关度；若存在大于0.2的情况，则认为这两个属性的相关程度不高，故无需继续进行判断；

6.2若在所有的总分类结果中，属性a和属性b的关联度仍是较高，则从其中任意选择一个属性保留，将另一个属性删除；若两个属性的关联度在总分类结果下存在偏低的情况，则将两个属性均保留。

上述提及的总分类结果指的是数据集本身自带的最终结果的类别。拿本文举例，本文衡量的是个人收入分类，具体包括年收入大于50w的，30-50w的，10-30w的，10w以下的。这个分类本身就存在于数据集中。

简单的描述一个数据集：

这是一个用于分类的数据集，必须包括最后的年收入的信息。

6.3对其他属性类别个数相同的属性根据步骤6.1-6.2操作进行相关度判断，并根据结果对数据集中的属性进行删除和保留，直到都所有属性类别个数相同的属性被判断完毕，更新数据集。

步骤(7)、采用属性加权来改变每个属性的权重，进而提升准确率。

7.1各总分类结果下寻求属性a中最大值类条件概率，记为p(ai|c1)，p(aj|c2)，…，p(ak|cn)；若属性a的属性类别重复出现，则说明属性a的属性类别与总分类结果的关联度偏低，认为属性a不是一个好的属性，故删除之；若属性a的属性类别均不一样，则说明属性a的属性类别与总分类结果的关联度较高，认为属性a是一个好的属性，故保留之，进行步骤7.2；

7.2根据步骤7.1得到的最大值类条件概率，计算属性a的平均置信度，即与总分类结果的关联度：

其中t的值越大，说明关联程度越高。

7.3根据步骤7.2得到的属性a的平均置信度，并依据上述步骤得到其他属性的置信度，计算次方系数α＝1-t，则属性加权后的公式为代表着使属性加权后的贝叶斯公式分子取最大值时对应的ci的值。

7.4根据步骤7.1-7.3，对其他的属性进行与总分类结果的相关性判断，并据此进行删除或者加权操作。

步骤(8)、分类判断过程。

多属性的贝叶斯基础公式为：

步骤(7)中所示：则有求出的ci即为元素对应的最大类别。

采用上述步骤对所有元素进行判定，ci最大值所对应的分类结果即为所需的分类结果。

本发明的有益效果是：

与现有技术相比，本发明能够应用于除了文本数据集以外的其他类型的数据集，包括离散型和连续型数据集在内，极大的提高了应用范围；而且能够提高一定的准确率，尤其是在属性类别过多的情况下，提升更为明显。

附图说明

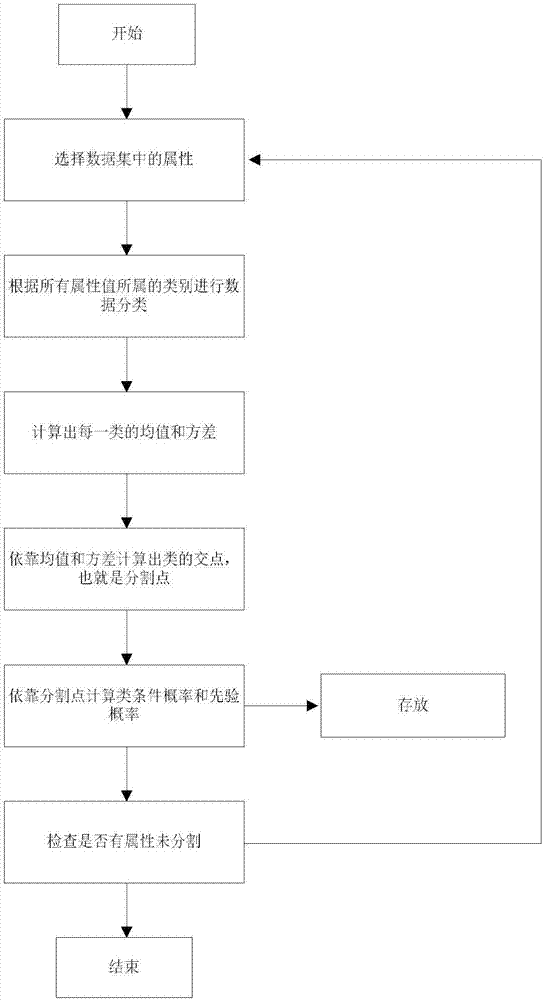
图1是基于连续型数据集的改进朴素贝叶斯算法框架图；

图2是采用高斯分布进行数据分割流程图。

具体实施方式

下面结合具体实施例对本发明做进一步的分析。

实施例1：如图1所示：

1)分析数据集，本数据集从人口数据库中抽取而来，可以用于甄别居民收入水平。其中的属性变量包含年龄，工种，学历，职业，人种等重要信息，包括了连续属性和离散属性，是一个很具有代表性的综合数据集。

2)为方便描述，对数据集中的离散文字型属性进行量化处理，比如职业，人种，工种等。具体处理方法为：将数据集中的所有非数字类信息全部换为数字，相同的非数字信息全部换为相同的数字，如将“工作”属性中，属性值为医生的全部换为数字1；属性值为程序员的，全部换为数字2；属性值为老师的，全部换为数字3…。不同属性之间可以使用相同的数字，比如“工作”和“工种”两种属性，在两个属性中都可以使用数字1,2,3…来代替属性原本的值。但是在同一属性中描述不同的属性值时，必须使用不同的数字，比如工作属性中，医生和程序员不能都使用数字1来代替，否则会出现极大的错分误差。

上述操作的目的是为了方便在下一步中计算类条件概率。如图2所示。

3)连续型属性数据离散化。

具体过程如下所示：

1.从数据集中选择一个连续型属性a。

2.数据集的分类结果为c1，c2，…，cn。统计整理属性a中分属不同类别的元素，分别命名为ac1，ac2，…，acn。

3.计算ac1，ac2，…，acn中的均值μ1，μ2，…，μn和方差

4.采用高斯公式计算相邻两个类别的交点，即ac1和ac2，ac2和ac3，…，acn-1和acn。分别将其命名为q1，q2，…，qn-1。交点的计算过程如下所示：

求出的x的值即代表了交点的位置

5.将交点q1，q2，…，qn-1按从小到大的顺序进行排列，并以其为分割点对属性a的所有值进行分类，其类别分别为a1，a2，…，an。

6.将同属一类的属性值用一个常数来代替(比如a1中的用数字1来代替，a2中的用2来代替…)。

7.采用上述方法对其他的连续属性进行处理，直到所有的连续属性皆处理完毕。

8.整理归并，得到初步处理之后的数据集。

4)在经过初步处理得到的上述数据集中，会有一部分属性类别(如ai，bn等)中没有属于某分类结果的元素，这种情况会对分类结果的准确率产生很大的影响。举个例子，比如ai中属于ck类的元素个数为0，即p(ai|ck)＝0，多属性贝叶斯公式为其中

p(x|ci)＝p(ax|ci)×p(bx|ci)×…×p(xx|ci)

当p(ax|ck)＝0时，会使p(ck|x)也等于0，这样的话，会将p(bx|ck)等其他属性的分类效果掩盖，造成一定程度上的错分。

为解决这一问题，引入拉普拉斯校准，即在所有属性类别中的每一个分类结果类别的元素数量上加1，不论其是否为0。比如在ai这个属性类别中，分别对属于c1，c2，…，cn分类类别的属性元素的个数上加1，这样可以在不影响数据的情况下避免0的出现。

5)求出各类的先验概率和类条件概率。

6)采用改进的关联规则算法来判断属性之间的相关性，判断出关联度较高的属性。具体过程如下例所示：

本文的数据集在属性a中，有a1，a2，a3，a4，a5五个类别，在属性b中，有b1，b2，b3三个类别，在属性d中，有d1，d2，d3三个类别，而总体的分类结果分为c1，c2，c3三个类别。

对于属性a和属性b，由于这两个属性的类别个数不同，其相关性相对较低，因此无需参与判别。

对属性b和属性d，这两个属性的类别个数相同，具有参与判断的基本条件。判断过程如下：

1.计算出p(b1|c1)，p(b2|c1)，p(b3|c1)，p(b1|c2)等共计9个的类条件概率

2.计算出p(d1|c1)，p(d2|c1)，p(d3|c1)，p(d1|c2)等共计9个的类条件概率

3.先判断c1类别下的关联程度，用p(d1|c1)，p(d2|c1)，p(d3|c1)各自减去p(b1|c1)，p(b2|c1)，p(b3|c1)，看在不重复(即属于c1类的所有类条件概率，不管是属于属性b还是属性d，都只出现一次)相减的情况下，是否有三个差的绝对值均小于0.2的情况出现。如果不是，则可以直接证明这两个属性的相关程度不高，无需继续进行判断；如果三个数的值小于0.2的情况出现了，则说明在分类结果c1中，属性b和d的相关度还是比较高的，需要继续判断在c2，c3中的情况。

4.采用6.3中的方法分别判断类别c2和c3中属性b和d的关联情况。如果在类别c2和c3中都有三个数小于0.2的情况出现，那么就说明在整体的分类结果中，属性b和属性d的关联度是较高的，可以从其中选择一个属性保留，将另外的一个属性删除。如果没有这种情况出现，说明在属性b和属性d中有一部分是关联度偏低的，因此属性b和属性d都保留。

5.对其他的类别个数相同的属性进行如上述步骤的相关性判断，并根据结果对数据集中的属性进行删除和保留，直到所有类别个数相同的属性都被判断完毕，更新数据集。

7)采用属性加权来改变每个属性的权重，进而提升准确率。本文采用上文中提到的属性a和分类结果c来进行描述，具体过程如下：

1.已知a为属性，有a1，a2，a3，a4，a5五个类别，c为总体分类结果，有c1，c2，c3三个类别。

2.分别对三个类找到三个类条件概率最大的值，即找到p(ai|c1)，p(aj|c2)，p(ak|c3)这三个类条件概率的最大值。i，j，k的值必须都不一样，如果出现重复，说明a的属性类别与分类效果的联系程度偏低，说明这不是一个好的属性，故删除之。

3.令其中t代表着属性a的平均置信度，即与分类结果的关联程度。t的值越大，说明关联程度越高。

4.令α＝1-t，则属性加权后的公式为

5.对其他的属性进行与分类结果的相关性判断，并据此进行删除或者加权操作。

8)分类判断过程。

多属性的贝叶斯基础公式为：

其主要作用是用来判断在某元素所有属性(即x)的具体值和类别已经确定的情况下，该元素属于ci这一分类结果的概率。

在本文中的具体作用是用来判断元素分别属于c1，c2，c3三个类别的概率，值最大的，就是属性最可能属于的类别。

在上式中，由于x的类别确定，因此p(x)是常量，所以只需对p(ci)×p(x|ci)的值进行判断。

在上述步骤7)中，本文采用了属性加权的方法，因此在这一步可以将属性加权加入贝叶斯基础公式中，如步骤7)中所示：则有求出的ci即为元素对应的最大类别。

采用上述步骤对所有元素进行判定，得到最终的分类结果。