一种泥石流沟道侵蚀量的计算方法与流程

本发明涉及到地质灾害防治工程技术领域，尤其涉及一种泥石流沟道侵蚀量的计算方法。

背景技术：

泥石流作为一种介于水流与碎屑流之间的两相流体，以其流速快、冲击强及暴发突然等运动特征，快速且强烈地作用于山岳地区，是强震区地质灾害后效应最主要的表现形式，将在未来较长时期内，严重危害灾区居民、城镇、交通、水利、电力设施等的安全，是影响灾后恢复重建的重要制约因素之一。全都有着极大的威胁。

泥石流沟道侵蚀作为一种主要的侵蚀机制，是由于沟道松散物质在一定深度的流体作用下，一旦流体对固体颗粒的驱动力大于其抵抗力时，便会失稳被裹挟进泥石流活动中，前人将这种起动机制称为“消防水管效应”，并认为流体强烈冲刷沟床堆积物是泥石流起动的关键因素。泥石流沟道侵蚀往往造成桥梁、堤防等基础的暴露等，其危害不亚于泥石流淤积。

目前有关泥石流沟道侵蚀的研究多是基于实验进行的定性描述或半定量分析，未能明晰泥石流侵蚀沟床的内在力学机理。如陈光曦等用实验定性研究了泥石流容重、流量、流速以及侵蚀基准面、沟道坡度、物质等因素对侵蚀的影响，则分类定性对比分析了泥石流侵蚀机理，认为稀性泥石流侵蚀与挟沙水流比较接近，而黏性泥石流的冲淤则接近滑坡。近来，虽然何思明等以上限定理为工具，对黏性泥石流对沟道土体的侵蚀能量条件进行了理论研究，但却缺乏力学机理解析，因而都难以定量描述侵蚀速率变化等侵蚀过程的发展，也不能对侵蚀深度等物理过程特征进行预测，因此，要以此为依据去指导泥石流沟道的治理还远远不够。

公开号为cn102943450a，公开日为2013年02月27日的中国专利文献公开了一种粘性泥石流沟沟床最大冲刷深度的测算方法，所述粘性泥石流沟包括原始沟床和在原始沟床上运动的泥石流体，其特征在于：所述粘性泥石流沟沟床最大冲刷深度的测算方法步骤如下：a、通过实际调查泥石流过流痕迹，确定泥石流体的深度h，单位m；通过泥石流容重计算公式计算或实际取样实测容重，确定泥石流体的重度γ1，单位kn/m³；通过实际取样实测容重，确定原始沟床堆积物质的重度γ2，单位kn/m³；通过大比例尺地形图测量计算，确定粘性泥石流沟的沟道纵比降j，单位‰；通过测定泥石流体的颗粒组成状况和浓度比，确定泥石流体的动摩擦角β，单位度；通过直接剪切或三轴试验，确定原始沟床堆积物质的内摩擦角，单位度；通过直接剪切或三轴试验，确定原始沟床堆积物质的粘性系数c，单位kpa；b、通过公式确定粘性泥石流沟沟床最大冲刷深度h1，单位m。

以该专利文献为代表的现有技术，均存在缺乏力学机理解析的缺陷，难以定量描述侵蚀速率变化等侵蚀过程的发展，也不能对侵蚀深度等物理过程特征进行预测，难以为实际防治工程提供依据。

技术实现要素：

本发明为了克服上述现有技术的缺陷，提供一种泥石流沟道侵蚀量的计算方法，本发明从泥石流沟道侵蚀的力学机理角度出发，将泥石流流深作为切入点，综合考虑沟床物质在因流动剪应力和自重静压带来的应力增加、因基质剪容和孔隙水压导致的强度衰减、以及因流体下渗产生的物质基础的联合作用，能够定量的描述侵蚀速率变化等侵蚀过程的发展，对侵蚀深度等物理过程特征进行预测，为防治工程基础埋深的设计提供依据，适应实际工程需求。

本发明通过下述技术方案实现：

一种泥石流沟道侵蚀量的计算方法，包括以下步骤：

a、收集获取泥石流流量q，测取泥石流沟道宽度b和泥石流平均流速vm，进而根据公式求得泥石流流深hd；

b、根据现场注水试验求得水流平均入渗速度vi和土体渗流系数k^*，再根据湿润锋计算公式计算得出沟床湿润锋zf，其中vi＞k^*；

c、根据voellmy模型，考虑颗粒摩擦、碰撞以及浆体的共同作用，收集所需要的参数，根据公式计算得出泥石流对沟床表面的流动剪应力τd；

式中，ξ为泥石流紊流系数，单位m/s²，vm为泥石流平均流速，单位m/s，γm为泥石流重度，单位kn·m^-3，μ为沟床摩擦系数，θ为沟床坡度，单位度，γmvm²/ξ为紊流项，μγmhdcosθ为摩擦项；

d、通过公式δσ＝γmhdcos²θ计算因泥石流自重静压而作用于沟床基质上的法向应力δσ、通过公式δτ＝γmhdsinθcosθ计算切向剪应力δτ、通过公式σbot＝(γmhd+γsdsc)cos²θ计算沟床面下dsc处沟床基质法向应力σbot以及通过公式τbot＝(γmhd+γsdsc)sinθcosθ计算切向剪应力τbot；

式中，γs为沟床基质饱和重度，单位kn·m^-3，γm为泥石流重度，单位kn·m^-3；

e、计算在侵蚀基准线处沟床基质所受泥石流流动和自重静压产生的驱动力fd＝τd+τbot，由莫尔-库伦准则推导出在沟床深度dsc处，其两侧岩土体因侧向水平应力而产生的抗剪强度式中k0为侧压力系数；

f、运用孔隙水压力增量公式δp＝bd(δσ+adδτ)计算沟床孔隙水压力增量，式中ad和bd为孔隙水压力系数；在沟床基质中，由于水流下渗而产生的土体初始孔隙水压力为：pini＝γwzfcos²θ，式中，γw为水体重度，单位kn·m^-3；总孔隙水压力为：ptot＝pini+δp；由莫尔-库伦准则推导出土体法向应力与孔隙水压力综合作用产生的抗剪强度

g、将泥石流沟床按坡度和沟谷宽度划分为若干段，用沟床侵蚀深度沿沟床长度进行积分，即得到整个沟床的侵蚀总量。

所述步骤e中，侧压力系数k0通过侧限条件下的单向固结仪进行测定或者在三轴压缩仪中测定。

本发明，适用于粘性泥石流规模、危险范围及堆积扇危险性评价。

本发明，适用于重度大于等于20kn/m³，粒径小于0.005mm，粘粒含量大于1％重量百分比的粘性泥石流沟。

本发明的有益效果主要表现在以下方面：

一、本发明，将沟道泥石流运动概化成明渠流，且泥石流流深hd的计算不考虑沟床水体入渗的影响；zf值会直接影响泥石流侵蚀沟床深度的确定，湿润锋将是侵蚀发生的下限面，这是因为湿润锋下层土体未受流体下渗的影响，故土体强度保持不变，不会失稳裹挟进泥石流活动中。通过泥石流起动模型和流域产/汇流模型作为基础，将泥石流流深作为切入点，综合考虑沟床物质在因流动剪应力和自重静压带来的应力增加、因基质剪容和孔隙水压导致的强度衰减、以及因流体下渗产生的物质基础的联合作用下，发生间断块状侵蚀后参与泥石流活动的过程机制，计算精度经试验验证，可靠度较高，能够定量的描述侵蚀速率变化等侵蚀过程的发展，能够更加准确的反应某段的侵蚀深度，为防治工程基础埋深的设计提供依据，适应实际工程需求。

二、本发明，从应力增加、强度衰减和物质基础三个方面出发，从力学机理角度解析了泥石流侵蚀速率变化等侵蚀过程的发展，定量分析了泥石流沿程沟床侵蚀机制及特征；从而能够对侵蚀深度等物理过程特征进行有效预测。

三、本发明，计算结果以美国地质勘探局的水槽实验的模型验证表明，模型计算值与实验观测值较为接近，且变化趋势相似，对侵蚀深度等物理过程特征具有可靠的预测价值，能够为防治工程基础埋深的设计提供依据。

附图说明

下面将结合说明书附图和具体实施方式对本发明作进一步的具体说明，其中：

图1为本发明的计算模型示意图；

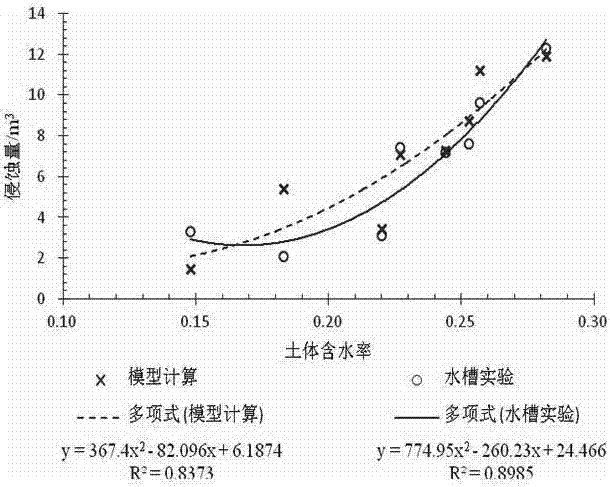
图2为本发明泥石流侵蚀沟床量的模型计算与实验对比曲线图；

图中标记：θi为第i段坡度，hdi为第i段泥石流流深，qi为第i段泥石流流量，dsci为第i段侵蚀深度。

具体实施方式

实施例1

一种泥石流沟道侵蚀量的计算方法，包括以下步骤：

a、收集获取泥石流流量q，测取泥石流沟道宽度b和泥石流平均流速vm，进而根据公式求得泥石流流深hd；

b、根据现场注水试验求得水流平均入渗速度vi和土体渗流系数k^*，再根据湿润锋计算公式计算得出沟床湿润锋zf，其中vi＞k^*；

c、根据voellmy模型，考虑颗粒摩擦、碰撞以及浆体的共同作用，收集所需要的参数，根据公式计算得出泥石流对沟床表面的流动剪应力τd；

式中，ξ为泥石流紊流系数，单位m/s²，vm为泥石流平均流速，单位m/s，γm为泥石流重度，单位kn·m^-3，μ为沟床摩擦系数，θ为沟床坡度，单位度，γmvm²/ξ为紊流项，μγmhdcosθ为摩擦项；

d、通过公式δσ＝γmhdcos²θ计算因泥石流自重静压而作用于沟床基质上的法向应力δσ、通过公式δτ＝γmhdsinθcosθ计算切向剪应力δτ、通过公式σbot＝(γmhd+γsdsc)cos²θ计算沟床面下dsc处沟床基质法向应力σbot以及通过公式τbot＝(γmhd+γsdsc)sinθcosθ计算切向剪应力τbot；

式中，γs为沟床基质饱和重度，单位kn·m^-3，γm为泥石流重度，单位kn·m^-3；

e、计算在侵蚀基准线处沟床基质所受泥石流流动和自重静压产生的驱动力fd＝τd+τbot，由莫尔-库伦准则推导出在沟床深度dsc处，其两侧岩土体因侧向水平应力而产生的抗剪强度式中k0为侧压力系数；

f、运用孔隙水压力增量公式δp＝bd(δσ+adδτ)计算沟床孔隙水压力增量，式中ad和bd为孔隙水压力系数；在沟床基质中，由于水流下渗而产生的土体初始孔隙水压力为：pini＝γwzfcos²θ，式中，γw为水体重度，单位kn·m^-3；总孔隙水压力为：ptot＝pini+δp；由莫尔-库伦准则推导出土体法向应力与孔隙水压力综合作用产生的抗剪强度

g、将泥石流沟床按坡度和沟谷宽度划分为若干段，用沟床侵蚀深度沿沟床长度进行积分，即得到整个沟床的侵蚀总量。

将沟道泥石流运动概化成明渠流，且泥石流流深hd的计算不考虑沟床水体入渗的影响；zf值会直接影响泥石流侵蚀沟床深度的确定，湿润锋将是侵蚀发生的下限面，这是因为湿润锋下层土体未受流体下渗的影响，故土体强度保持不变，不会失稳裹挟进泥石流活动中。通过泥石流起动模型和流域产/汇流模型作为基础，将泥石流流深作为切入点，综合考虑沟床物质在因流动剪应力和自重静压带来的应力增加、因基质剪容和孔隙水压导致的强度衰减、以及因流体下渗产生的物质基础的联合作用下，发生间断块状侵蚀后参与泥石流活动的过程机制，计算精度经试验验证，可靠度较高，能够定量的描述侵蚀速率变化等侵蚀过程的发展，能够更加准确的反应某段的侵蚀深度，为防治工程基础埋深的设计提供依据，适应实际工程需求。

实施例2

一种泥石流沟道侵蚀量的计算方法，包括以下步骤：

a、收集获取泥石流流量q，测取泥石流沟道宽度b和泥石流平均流速vm，进而根据公式求得泥石流流深hd；

b、根据现场注水试验求得水流平均入渗速度vi和土体渗流系数k^*，再根据湿润锋计算公式计算得出沟床湿润锋zf，其中vi＞k^*；

c、根据voellmy模型，考虑颗粒摩擦、碰撞以及浆体的共同作用，收集所需要的参数，根据公式计算得出泥石流对沟床表面的流动剪应力τd；

式中，ξ为泥石流紊流系数，单位m/s²，vm为泥石流平均流速，单位m/s，γm为泥石流重度，单位kn·m^-3，μ为沟床摩擦系数，θ为沟床坡度，单位度，γmvm²/ξ为紊流项，μγmhdcosθ为摩擦项；

d、通过公式δσ＝γmhdcos²θ计算因泥石流自重静压而作用于沟床基质上的法向应力δσ、通过公式δτ＝γmhdsinθcosθ计算切向剪应力δτ、通过公式σbot＝(γmhd+γsdsc)cos²θ计算沟床面下dsc处沟床基质法向应力σbot以及通过公式τbot＝(γmhd+γsdsc)sinθcosθ计算切向剪应力τbot；

式中，γs为沟床基质饱和重度，单位kn·m^-3，γm为泥石流重度，单位kn·m^-3；

e、计算在侵蚀基准线处沟床基质所受泥石流流动和自重静压产生的驱动力fd＝τd+τbot，由莫尔-库伦准则推导出在沟床深度dsc处，其两侧岩土体因侧向水平应力而产生的抗剪强度式中k0为侧压力系数；

f、运用孔隙水压力增量公式δp＝bd(δσ+adδτ)计算沟床孔隙水压力增量，式中ad和bd为孔隙水压力系数；在沟床基质中，由于水流下渗而产生的土体初始孔隙水压力为：pini＝γwzfcos²θ，式中，γw为水体重度，单位kn·m^-3；总孔隙水压力为：ptot＝pini+δp；由莫尔-库伦准则推导出土体法向应力与孔隙水压力综合作用产生的抗剪强度

g、将泥石流沟床按坡度和沟谷宽度划分为若干段，用沟床侵蚀深度沿沟床长度进行积分，即得到整个沟床的侵蚀总量。

所述步骤e中，侧压力系数k0通过侧限条件下的单向固结仪进行测定或者在三轴压缩仪中测定。

实施例3

一种泥石流沟道侵蚀量的计算方法，包括以下步骤：

a、收集获取泥石流流量q，测取泥石流沟道宽度b和泥石流平均流速vm，进而根据公式求得泥石流流深hd；

b、根据现场注水试验求得水流平均入渗速度vi和土体渗流系数k^*，再根据湿润锋计算公式计算得出沟床湿润锋zf，其中vi＞k^*；

c、根据voellmy模型，考虑颗粒摩擦、碰撞以及浆体的共同作用，收集所需要的参数，根据公式计算得出泥石流对沟床表面的流动剪应力τd；

式中，ξ为泥石流紊流系数，单位m/s²，vm为泥石流平均流速，单位m/s，γm为泥石流重度，单位kn·m^-3，μ为沟床摩擦系数，θ为沟床坡度，单位度，γmvm²/ξ为紊流项，μγmhdcosθ为摩擦项；

d、通过公式δσ＝γmhdcos²θ计算因泥石流自重静压而作用于沟床基质上的法向应力δσ、通过公式δτ＝γmhdsinθcosθ计算切向剪应力δτ、通过公式σbot＝(γmhd+γsdsc)cos²θ计算沟床面下dsc处沟床基质法向应力σbot以及通过公式τbot＝(γmhd+γsdsc)sinθcosθ计算切向剪应力τbot；

式中，γs为沟床基质饱和重度，单位kn·m^-3，γm为泥石流重度，单位kn·m^-3；

e、计算在侵蚀基准线处沟床基质所受泥石流流动和自重静压产生的驱动力fd＝τd+τbot，由莫尔-库伦准则推导出在沟床深度dsc处，其两侧岩土体因侧向水平应力而产生的抗剪强度式中k0为侧压力系数；

f、运用孔隙水压力增量公式δp＝bd(δσ+adδτ)计算沟床孔隙水压力增量，式中ad和bd为孔隙水压力系数；在沟床基质中，由于水流下渗而产生的土体初始孔隙水压力为：pini＝γwzfcos²θ，式中，γw为水体重度，单位kn·m^-3；总孔隙水压力为：ptot＝pini+δp；由莫尔-库伦准则推导出土体法向应力与孔隙水压力综合作用产生的抗剪强度

g、将泥石流沟床按坡度和沟谷宽度划分为若干段，用沟床侵蚀深度沿沟床长度进行积分，即得到整个沟床的侵蚀总量。

所述步骤e中，侧压力系数k0通过侧限条件下的单向固结仪进行测定或者在三轴压缩仪中测定。

适用于粘性泥石流规模、危险范围及堆积扇危险性评价。

适用于重度大于等于20kn/m³，粒径小于0.005mm，粘粒含量大于1％重量百分比的粘性泥石流沟。

从应力增加、强度衰减和物质基础三个方面出发，从力学机理角度解析了泥石流侵蚀速率变化等侵蚀过程的发展，定量分析了泥石流沿程沟床侵蚀机制及特征；从而能够对侵蚀深度等物理过程特征进行有效预测。

为了验证理论模型的准确性与适用性，本发明将模型计算结果与实测值进行对比分析，由于野外泥石流现场数据很难准确获取，故本发明利用美国地质勘探局的水槽实验数据验证模型。

实验水槽长95m，宽2m，固体坡度31°，顶部水箱储存泥石流体6m³，沟床中段铺垫均厚12cm的碎石土，考虑其不同含水率的情况下，泥石流突然释放后侵蚀该段沟床物质量的变化；泥石流侵蚀沟床量的模型计算值与实验值对比如表1所示。

表1为泥石流侵蚀沟床量的模型计算值与实验值对比表

表1

对比结果显示：

首先，从单个实验来看，理论模型计算结果与实验观测值较为接近，a-f前6次实验所得侵蚀方量的相对误差仅介于-4.26％-16.67％之间，而g、h两次实验结果偏差较大，是因为在水槽实验数据验证模型中，泥石流流速变量对侵蚀深度或侵蚀总量影响最为显著，所以g实验中虽然土体含水率较低，但由于泥石流流速较大，故计算侵蚀总量较实验值偏大；而h实验中泥石流流速大幅降低，故模型计算值偏小。

其次，从a-h这8次实验的总体趋势来看，模型计算结果较为合理。8次实验的计算侵蚀方量数列的均值为7.06，标准差为3.37；而实测侵蚀方量数列的均值为6.58，标准差为3.30，对比可得，均值的相对误差为7.44％，标准差的相对误差仅为2.22％，这表明两组数列具有相似的平均值和离散程度。

另外，从图2亦可发现，模型计算值与实验值的拟合回归方程也具有相近的变化趋势。

综上所述，据美国地质勘探局的水槽实验数据验证模型的实验结果对比分析，本研究构建的理论模型能够较为准确地计算泥石流侵蚀沟床深度和侵蚀总量，计算结果真实可靠，可用于泥石流固体物质总量的计算，为泥石流规模、危险范围及堆积扇危险性评价奠定理论基础。