一种基于开方分解谱表示法的平稳脉动风场模拟方法与流程

本发明涉及土木工程结构抗风设计方法，具体涉及一种基于开方分解谱表示法的平稳脉动风场模拟方法。

背景技术：

在大跨度桥梁、高层建筑等的风致动力响应分析中，由于需要考虑结构和气动的非线性，传统的频域分析方法不能满足要求，需要采用基于时程的非线性动力响应分析。在非线性时程分析中，模拟结构位置处的脉动风场是一个基本环节，也是最为重要的环节。在众多模拟方法中，谱表示法的形式较为简单，即只通过三角函数的叠加模拟得到，且具有严密的推导作为理论支撑，是平稳风场模拟的常用方法。为了提高模拟效率，该方法常与fft技术相结合。

在上述方法中，由于风场功率谱矩阵的正定性得不到保证，例如自功率谱值为0的频率处，从而导致cholesky分解不能实施，从而影响了风场模拟的进行。因此需要提出一种更为有效且适合于风场谱表示模拟方法的矩阵分解方法。

技术实现要素：

发明目的：本发明的目的是为了解决风场模拟中在局部频率点处不能对功率谱矩阵进行cholesky分解的问题，提供一种通过对功率谱矩阵进行开方分解以使得谱表示法能够适用于更多情况下的功率谱矩阵的基于开方分解谱表示法的平稳脉动风场模拟方法。

技术方案：本发明所述的一种基于开方分解谱表示法的平稳脉动风场模拟方法，包括如下步骤：

(1)将平稳脉动风场进行离散化，确定所需模拟风过程的离散点个数n，此时随机风场的模拟转换为一维多变量(1d-nv)随机过程的模拟，其包含以下n个变量：v1(t),v2(t),…,vn(t)；

(2)根据风场的离散结果，确定随机风场的功率谱矩阵：

其中，sjj(ω)是n个自功率谱矩阵，j＝1,2,…,n；sjk(ω)为互功率谱矩阵，j,k＝1,2,…,n,j≠k；所述功率谱矩阵进一步表示为：

其中，jk(ω)是相干函数矩阵；为体现行波效应项的相位角；

(3)通过对功率谱矩阵进行矩阵的开方分解，得到新的多维高斯功率谱矩阵：

svv(ω)＝h(ω)h^t(ω)

(4)随机生成在[0,2π]范围内均匀分布的n²个随机相位角j,k＝1,2,…,n；

(5)使用基于谱表示法的三角函数叠加方法，生成各个点的风过程时程：

其中，m是频率步数；ωl＝lδω为频率步长；δω＝ωu/m为频率增量；ωu为截断频率。

步骤(5)中，所述频率步数m为2的整数次方；所述截断频率ωu取当高于该值后功率谱函数s(ω)的值为无穷小，或小到可以忽略不计。

有益效果：与现有技术相比，本发明具有以下优点：采用本发明模拟随机平稳风场是，不需要传统方法中所需的cholesky分解，而使用开方分解进行功率谱矩阵分解，从而克服了传统方法中对功率谱矩阵要求为对称正定的要求，而开方分解只需要功率谱矩阵满足对称非负定，从而保证当某些频率处即使功率谱矩阵的特征值存在0值仍可以继续进行分解；此外，该开方分解方法克服了cholesky分解方法分解后矩阵出现大量0元素的缺点，更合理地考虑了各点之间的关联性。

附图说明

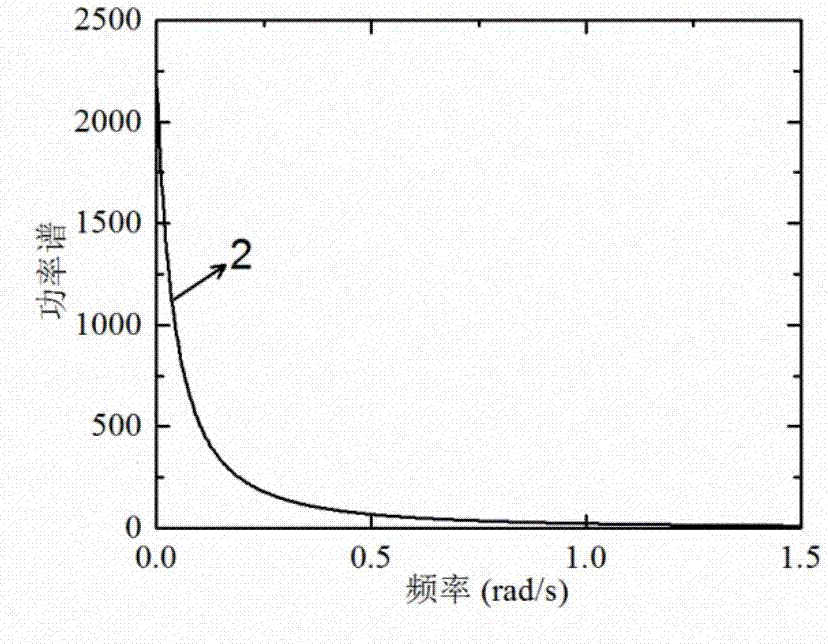
图1(a)-(c)是第一个点、第二个点和第三个点的自功率谱；

图2(a)-(c)是第一个点、第二个点和第三个点的脉动时程；

图3(a)-(c)是第一个点、第二个点和第三个点的风过程的平均自功率谱；

图4(a)是第一个点与第二个点的互自功率谱的平均相位角与目标值的比较；

图4(b)是第二个点与第三个点的互自功率谱的平均相位角与目标值的比较；

图4(c)是第一个点与第三个点的互自功率谱的平均相位角与目标值的比较。

具体实施方式

下面结合附图对本发明的技术方案作进一步说明。

本实施方法以模拟一个一维三变量随机风场为例进行说明：

(1)模拟的点为沿着同一垂线分布的三个点，它们的高度分别为100m，110m，120m。

(2)假定各点的自功率谱为：

其中，zj是第j点的高度，u*是剪切波速，u(zj)是在高度zj处的平均风速，其可以通过以下经验公式得到：

其中，k是vonkarman常数，粗糙长度z0取2.0m；得到各点高度处的平均风速为：

u(z1＝120m)＝64.4m/s

u(z2＝110m)＝63.0m/s

u(z3＝100m)＝61.5m/s

基于上述参数，得到的各点的自功率谱如图1(a)、图1(b)和1(c)所示，图1(a)-(c)中，1表示第一个点的自功率谱；2表示第二个点的自功率谱；3表示第三个点的自功率谱。

相干函数取为：

其中，cz和cx的值分别设为10和6；

体现行波效应的视波速为10m/s；根据上述自功率谱与相干函数，即可以确定互功率谱函数，从而得到功率谱矩阵。

(3)通过对功率谱矩阵进行矩阵的开方分解，得到分解后的矩阵：

svv(ω)＝h(ω)h^t(ω)

(4)随机生成在[0,2π]范围内均匀分布的n²个随机相位角(j,k＝1,2,…,n)。

(5)使用基于谱表示法的三角函数叠加方法，生成各个点的风过程时程：

其中，m是频率步数，为了使用傅里叶变化一般可以2的整数次方，本实施例中m取512；ωl＝lδω为频率步长；频率增量为δω＝ωu/m；ωu为截断频率，取1.5rad/s，其一般可以取当高于该值后功率谱函数s(ω)的值为无穷小，或小到可以忽略不计。

通过上述模拟方法，模拟的三个点的脉动风速如图2(a)、图2(b)和图2(c)所示，图2(a)-(c)中，4表示第一个点的脉动时程；5表示第二个点的脉动时程；6表示第三个点的脉动时程。通过模拟1000组这样的风场，并对其自功率谱以及互功率谱的相位角进行分析，得到各点的平均自功率谱如图如图3(a)、图3(b)和图3(c)所示，图3(a)-(c)中，7表示第一个点的风过程的平均自功率谱；8表示第二个点的风过程的平均自功率谱；9表示第三个点的风过程的平均自功率谱；可见，各点的平均自功率谱与目标自功率谱一致；各点间互功率谱的平均相位角如图如图4(a)、图4(b)和图4(c)所示，图4(a)中，10表示第一个点与第二个点的互自功率谱的相位角的目标值；11表示第一个点与第二个点的互自功率谱的相位角的平均值；图4(b)中，12表示第二个点与第三个点的互自功率谱的相位角的目标值；13表示第二个点与第三个点的互自功率谱的相位角的平均值；图4(c)中，14表示第一个点与第三个点的互自功率谱的相位角的目标值；15表示第一个点与第三个点的互自功率谱的相位角的平均值；也与目标值保持一致，从而可以说明模拟方法的合理性。