基于两维不可分DFT调制滤波器组的图像去噪方法与流程

本发明涉及滤波器组技术领域，具体涉及一种基于两维不可分dft调制滤波器组的图像去噪方法。

背景技术：

多速率滤波器组已广泛应用于图像处理、音视频信号处理、数字通信、计算机视觉和纹理识别与分类等领域中。数字图像去噪的方法大致可以分为空域和变换域两个大方面。空域去噪可分为非线性的空域去噪和线性的空域去噪，它对图像进行去噪处理的过程是在图像的两维空间之中。中值滤波、多副图像平均法以及邻域平均法等都是空域去噪的方法，这些方法通常是利用不同种类的模板，再对图像各邻域间像素进行平滑处理，进而达到图像去噪的目的。与空域去噪方法有所不同，先对图像进行某种变换然后再进行后续工作的方法称为变换域去噪办法。具体讲就是图像先从时域转换到变换域，接着对转换后的变换域上的系数进行一系列操作，最后图像再转换到空间域，这是经过了对变换域进行反变换操作的过程，经过整个操作可以完成图像去噪的效果。目前大部分的两维dft调制滤波器组的图像去噪方法还停留在两维可分dft去噪方法或由一维扩展到两维的不可分去噪方法。两维复滤波器组有着良好的频率方向选择性，对于图像的纹理、边缘能够很好的表示，所以直接利用两维不可分dft调制滤波器组进行图像去噪的方法有待研究。

技术实现要素：

本发明所要解决的是现有基于两维dft调制滤波器组的图像去噪方法对于图像的边缘和纹理处理不够细致的问题，提供一种基于两维不可分dft调制滤波器组的图像去噪方法。

为解决上述问题，本发明是通过以下技术方案实现的：

基于两维不可分dft调制滤波器组的图像去噪方法，包括如下步骤：

步骤1，利用第一个两维不可分dft调制滤波器组的分析滤波器组对噪声图像进行分解，得到一次噪声图像的子带系数；同时利用第二个两维不可分dft调制滤波器组的分析滤波器组对噪声图像进行分解，得到二次噪声图像的子带系数；

步骤2，通过平滑沿着椭圆窗口的一次噪声图像的子带系数的原始能量分布，得到一次噪声图像的子带系数的能量分布估计值；

步骤3，基于步骤1所得一次噪声图像的子带系数和步骤2所得一次噪声图像的子带系数的能量分布估计值，经过第一次维纳滤波得到一次去噪图像的子带系数的估计值；

步骤4，利用第一个两维不可分dft调制滤波器组的综合滤波器组对步骤3所得一次去噪图像的子带系数的估计值进行重构，得到引导图像；

步骤5，利用第二个两维不可分dft调制滤波器组的分析滤波器组对步骤4所得引导图像进行分解，得到引导图像的子带系数；

步骤6，通过平滑沿着椭圆窗口的引导图像的子带系数的原始能量分布，得到引导图像的子带系数的能量分布估计值；

步骤7，基于步骤1所得二次噪声图像的子带系数和步骤6所得引导图像的子带系数的能量分布估计值，经过第二次维纳滤波得到二次去噪图像的子带系数的估计值；

步骤8，利用第二个两维不可分dft调制滤波器组的综合滤波器组对步骤7所得二次去噪图像的子带系数的估计值进行重构，得到最终去噪图像。

与现有技术相比，本发明在图像去噪方面有着一定的优势，尤其在处理非均匀纹理细节图像时，可得到更高的峰值信噪比(psnr)，对于纹理区域的图像可以实现更好的视觉效果。

附图说明

图1是本发明基于两维不可分dft调制滤波器组的图像去噪方法的流程图。

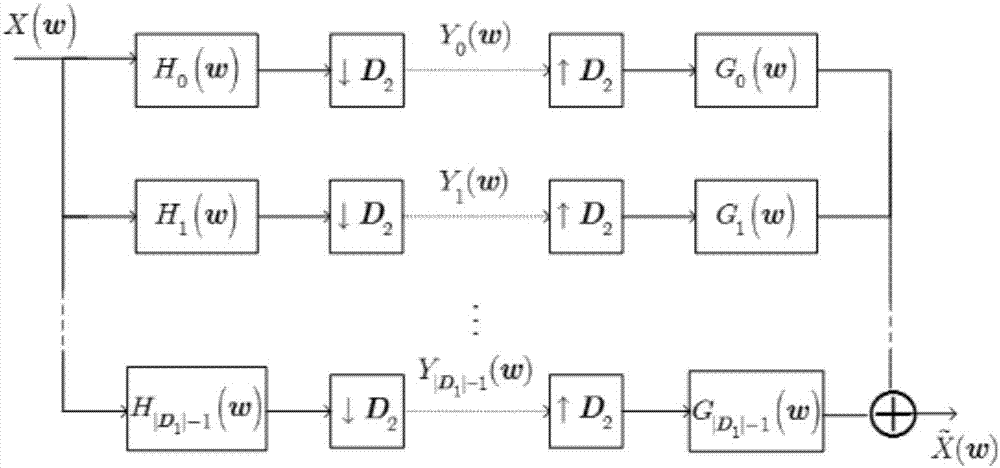
图2是两维dft调制滤波器组的基本结构。

图3是实例2中‘lena’图像的四个局部区域的视觉效果对比图；其中(a)为区域([1,81]×[20,100])，(b)为区域([100,180]×[360,440])，(c)为区域([80,160]×[170,250])，(d)为区域([20,100]×[240,320])。

图4是实例2中‘barbara’图像局部区域的视觉效果对比图；其中(a)为原始图像，(b)为噪声图像，(c)为两维可分dft去噪图像，(d)为本发明算法去噪图像。

具体实施方式

一种基于两维不可分dft调制滤波器组的图像去噪方法，如图1所示，该方法中子带系数的噪声图像经过dft-fb1和dft-fb2进行了两次局部维纳滤波操作，具体包括如下步骤：

第一步：第一次使用局部维纳滤波前，噪声图像y(n)＝x(n)+ε(n)首先通过第一个两维不可分dft调制滤波器组的分析滤波器组分解到一次噪声图像子带系数中，这个过程代表图1中的‘dft-fb1’。再将噪声图像经过第二个两维不可分dft调制滤波器组的分析滤波器组，得到二次噪声图像的子带系数，这个过程代表图1中噪声图像下边的‘dft-fb2’。一次噪声图像子带信号和二次噪声图像子带信号的频域分别为：

其中一次噪声图像子带系数和二次噪声图像子带系数的均值和方差分别为：

其中e代表期望值。第二步：从一次噪声图像子带系数中估计一次噪声图像的子带能量分布。这个过程代表图1中的‘eed-dw1’。

首先分析两维不可分dft调制滤波器组的方向选择性。当两维dft调制滤波器组的调制矩阵为d1时，其集合为其中i＝0,1,...|d1|-1。每个子带滤波器的频域支撑位置可以通过方位角和原始频域支撑的中心距离来确定，距离被称为子带滤波器的频率特征。设a＝u(1)，b＝u(2)，那么子带滤波器的方位角α(m,k)可以通过下标的方法来定义：

其中

同理，频率特征ρ(m,k)也可以通过下标的方法来定义：

其中

角度α(m,k)描述了子带滤波器的方向，表明它可以提取沿着方向α(m,k)变化的两维复值信号。频率特征ρ(m,k)代表子带滤波器的频域选择。

根据子带滤波器的方向性可知，在第i个子带中，图像的大幅度系数通常集中在沿着方向π/2+π/4+α(m,k)的能量簇。并且，能量簇的宽度与子带滤波器的特征频率ρ(m,k)相关。也就是说，子带滤波器沿着方向π/2+π/4+α(m,k)的特征频率越ρ(m,k)大，则图像的边缘和纹理越清晰。因此，沿着方向π/2+π/4+α(m,k)的椭圆窗定义为：

椭圆窗的主半轴相当于沿着直线ny/nx＝tan(π/2+π/4+α(m,k))的r1(1+|d12|ρ(m,k))，次半轴相当于沿着直线ny/nx＝tanα(m,k)的r1/(1+|d12|ρ(m,k))。由此可得，根据上式计算所得的窗是沿着方向π/2+π/4+α(m,k)的长椭圆窗，它与从第i个子带信号提取的边缘和纹理相匹配。此外，当特征频率较大时，椭圆窗的主半轴与次半轴的比值也更大，这与子带滤波器的频率选择性是一致的。乘数|d12|是dft-fb1的采样因子。我们知道，采样因子可以稀释子带的能量簇。因此，一个更大的采样因子需要一个更扁的椭圆窗。在窗内的图像像素值近似等于其中[x]代表实数x的整数部分。

平滑沿着椭圆窗口的一次噪声图像子带系数的原始能量分布，我们可以得到一次噪声图像的子带能量分布的估计值为下式：

其中{x}+＝max{x,0}，代表窗尺寸。

第三步：基于上式得到的估计值以及一次噪声图像的子带系数通过在流程图中标记为‘lwf1’的第一次维纳滤波估计出一次去噪图像的子带系数。

第四步：第一次维纳滤波后的一次去噪图像的子带系数和一次噪声图像低通子带系数(通常，大多数基于变换的图像去噪算法的低通子带是不经过处理的)经过dft-fb1的综合滤波器组处理后，我们可以得到一个噪声比较小的引导图像

第五步：在第二次维纳滤波前，引导图像通过调制矩阵和采样矩阵分别为d21和d22的第二个两维不可分dft调制滤波器组的分析滤波器组分解到引导图像的子带系数中，这个过程代表图1中的‘dft-fb2’。引导图像的子带系数可以表示为

第六步：根据第五步所得的引导图像的子带系数估计出引导图像的子带能量分布。这个过程代表图1中的‘eed-dw2’。

与第一次维纳滤波所得窗函数相似，第二次维纳滤波的椭圆窗定义为：

由于引导图像相比于噪声图像包含更少的噪声，故其中的r2是比r1更小的数字。同样，平滑沿着椭圆窗口的引导图像的子带系数的原始能量分布，我们可以得到引导图像的子带能量分布的估计值，可表示为：

第七步：利用上式以及噪声图像经过‘dft-fb2’的分析滤波器组得到的二次噪声图像子带系数通过在流程图中标记为‘lwf2’的第二次维纳滤波估计出二次去噪图像的子带系数。

第八步：第二次维纳滤波后的二次去噪图像的子带系数和二次噪声图像低通子带系数经过‘dft-fb2’的综合滤波器组处理后，可以重构得到最终的去噪图像

实例1：

为了更好地体现本发明的方向和频率选择性，我们将检测它处理不同图像的结果。测试图像选择三种有代表性的图像，分别为：一、尺寸为512×512的8bit的灰度图像‘lena’，主要由平滑的区域和边缘构成；二、尺寸为512×512的8bit的灰度图像‘barbara’，拥有丰富的、不均匀的纹理细节；三、尺寸为256×256的8bit的灰度图像‘house’，拥有丰富的、均匀的纹理细节。图2是两维dft调制滤波器组的基本结构。现在我们比较两维可分的dft调制滤波器组(简称为可分)和两维不可分的dft调制滤波器组(简称为不可分)分别应用双重局部维纳滤波后对图像去噪的峰值信噪比。其中长度为35×35的两维可分的过采样近似完全重构的dft调制滤波器组是由两个长度为1×35的一维过采样近似完全重构的dft调制滤波器组通过张量积产生的。两维不可分dft调制滤波器组的调制矩阵为采样矩阵为空域支撑为la＝ls＝17，得到的滤波器组长度为1225×1，与两维可分滤波器组长度相同。σ²代表两维高斯白噪声的方差，表1给出了两维不可分图像去噪方法与两维可分图像去噪方法得到的去噪图像的峰值信噪比(psnr)。

表1两维不可分图像去噪方法与两维可分图像去噪方法的性能对比

由表1可以看出，本发明方法在三种类型的测试图像中都得到优化，说明本发明在图像平滑的区域和边缘以及丰富的均匀和非均匀纹理细节方面的整体性能更好。

实例2：

大多数的算法可以在平滑区域实现高的视觉质量，本发明的优势主要在于保留图像的边缘和纹理信息。图3比较了‘lena’图像的四个局部区域，(a)([1,81]×[20,100])代表平滑区域，(b)([100,180]×[360,440])代表边缘区域，(c)([80,160]×[170,250])代表纹理区域，(d)([20,100]×[240,320])代表纹理加平滑区域。在图3的每个局部区域图中，顶部左上角是‘lena’原图，顶部右上角是噪声图像，底部左下角是基于两维可分dft调制滤波器组的双重局部维纳滤波的去噪图像，底部右下角是基于两维不可分dft调制滤波器组的双重局部维纳滤波的去噪图像。噪声水平为σ＝15，相比较的算法其四个局部区域(a)，(b)，(c)，(d)的局部psnr分别为36.99，32.86，32.44和34.45。本发明方法的四个区域的局部psnr分别为36.64，33.06，32.96和35.11。可以看出，本发明方法所得的去噪图像在边缘和纹理区域视觉效果更佳，并且整体视觉效果更好一些。

接下来，我们对比一下本发明方法与基于两维可分dft调制滤波器组的双重维纳滤波的去噪方法在去噪图像‘barbara’中的一个非均匀纹理区域的psnr。图4比较了‘barbara’图像中一个非均匀纹理区域，(a)原始图像，(b)噪声图像，(c)两维可分dft去噪图像，(d)本发明方法的去噪图像。噪声水平为σ＝15，如图4所示，两维可分图像去噪方法的局部psnr为30.00，本发明两维不可分图像去噪方法的局部psnr为31.09，表明本发明方法在非均匀纹理图像中的视觉效果更佳。

综上，本发明方法在图像去噪方面具有一定的优势，不仅在平滑的区域和边缘得到优化，且在丰富的均匀和非均匀纹理细节效果更佳。

本发明先后两次利用两维不可分dft调制滤波器组和局部维纳滤波，通过匹配子带滤波器组的频率方向确定两个椭圆窗，进而估计出图像子带能量分布，最后得出去噪图像的子带系数。将本发明方法计算出的常用测试图像的峰值信噪比(psnr)和基于两维可分dft调制滤波器组的图像去噪的psnr相比较，实验表明，本发明可得到有竞争力的psnr且去噪图像拥有丰富的非均匀纹理细节，可得到视觉效果更好的图像。