一种O2O外卖平台智能调度与路线优化方法与流程

本发明属于物流调度与优化技术，特别是一种o2o外卖平台订单智能调度与路线优化方法。
背景技术：
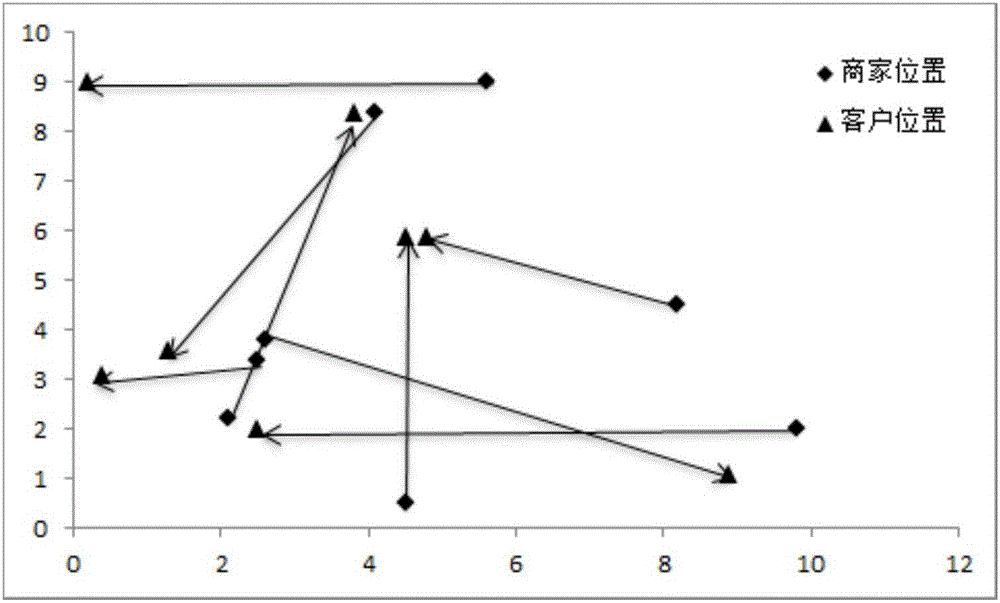
：当前有很多o2o外卖平台，如百度外卖、饿了么、美团等，而外卖调度与配送作为餐饮o2o的重要支撑环节，其优劣直接影响互联网餐饮外卖的进一步扩张与发展。然而，由于区域性限制、时效性要求高、利润点相对较低等诸多原因，外卖配送物流成本居高不下，外卖调度与配送优化是外卖平台最大的难题。目前专门针对o2o外卖平台外卖调度与配送路线的公开文献较少，多数仍然采用传统物流配送优化模型及其变形，如设施选址-分配问题(lap)、路径优化问题(vrp)和同时送取货vrp问题(vrpspd)。lap重点是确定配送中心最佳位置，不允许路线巡回访问；vrp虽允许路线巡回访问，但要求开始与结束位置都必须为同一配送中心，且二者都为先从配送中心取货，后向客户配送的过程；vrpspd为同时送取货的车辆路径问题，所有配送货物都要从配送中心装车送至客户，所有从客户装车的货物都要送至配送中心。但这些方法应用于o2o外卖平台订单调度与配送路线选取时效果都不理想：1)由于外卖配送一般会划分合理的区域范围且距离不会太远，同时为了避免影响餐品质量与口味，一般要求出餐后30分钟送达客户，有严格的配送时间约束；2)传统物流配送优化问题都有固定的配送中心(一般中心较少)且车辆都从中心出发最终回到中心的闭环结构，而外卖配送路线优化问题，必须保证先去订单的商家取餐、后配送到客户，商家、客户不能同等对待，订单的商家、客户位置为动态需求且调度时配送员位置也不固定；3)传统物流配送优化问题调度之后转化为旅行商问题(tsp)，寻找最优路线属于np问题，多采用启发式算法求解，算法效率普遍较低，而o2o外卖平台订单非常多且比较集中，需要快速指派配送员并给出推荐路线。这些因素共同影响，使得o2o外卖平台外卖调度与配送优化问题的处理更为复杂。技术实现要素：为解决现有技术存在的上述问题，本发明要提出一种同时考虑配送时间约束、商家与客户位置依据订单需求动态变化且快速高效的o2o外卖平台智能调度与路线优化方法。为了实现上述目的，本发明的技术方案如下：一种o2o外卖平台智能调度与路线优化方法，包括以下步骤：a、对外卖订单数据进行预处理a1、依据当前未配送外卖订单记录，令k为已指派尚未完成配送的外卖订单数，k’为未指派配送员的外卖订单数，则lsk或lsk’分别为第k或k’个订单的商家位置，lck或lck’分别为第k或k’个订单的客户位置，由于位置主要用于计算距离，而外卖配送的区域范围非常小，用直线距离取代地理空间距离对结果不产生影响；k＝1,2,…,k，k’＝1,2,…,k’；a2、令该配送区域内配送员数为n，xki＝1或xk’i＝1分别表示订单k或k’指派给配送员i，xki＝0或xk’i＝0分别表示订单k或k’未指派给配送员i；xi(s,t)表示配送员i是否需要走边(s,t)，即从s位置直接沿着边(s,t)去t位置，其中是为1，否为0，边长记为l(s,t)；订单k生效时刻为tk0,订单k的客户希望最迟送达时刻为ltk，配送员到订单k的商家取餐的时刻为tks，配送员把订单k送达客户的时刻为tkt；s,t∈{(k+k’)个订单的商家或客户位置}，i＝1,2,…,n；a3、给定配送员平均配送速度为v，单位时间配送成本为uc，超出指定配送时间的延迟单位时间成本为dc，通过当前配送员的手机gps获取位置数据。计算当前所有k’+k个外卖订单的所有商家lsk、客户位置lck的边长，边长矩阵l＝(l(s,t))2k×2k，边长实际为两点s(s1,s2)、t(t1,t2)的欧氏距离，如式(1)所示：b、快速生成外卖订单智能指派模型b1、给定配送员已指派未配送的订单容量约束为q；b2、判断：如果k’+k≤n×q，则全部指派，否则只取k’中先下订单的(n×q-k)作为本次要指派的订单，其他(k’+k-n×q)个订单下次调度时指派，同时将本次需要指派的订单作为k’。b3、将当前所有未指派订单按照订单生成的先后顺序排序，订单序号i越小，表示订单生成越早，应该更优先被指派；设定当前未指派订单序号k’＝1；b4、判断：当前是否有空闲配送员i，i＝1,2,…,n，有则将订单k’指派给配送员i，即xk’i＝1，转到步骤b7，否则转到步骤b5；b5、计算当前订单k’到所有已指派未完成订单的距离，如式(2)所示：d(k’,k)＝l(lsk’,lsk)+l(lck’,lck),k＝1,2,…,k(2)b6、将d(k’,k)按照距离由小到大的顺序排列，对应排序后的订单序号kmin＝1,2,…,k，之后为订单k’指派配送员：b61、设定当前排序后的订单序号kmin＝1；b62、订单kmin已指派的配送员为imin，判断：如果配送员imin已指派未完成数：则转到步骤b63；否则转到步骤b64。b63、令kmin＝kmin+1，判断：如果kmin≤k，转到步骤b62；否则转到步骤b8。b64、将k’指定给配送员imin，即xk’imin＝1。b7、令当前商品节点序号k’＝k’+1，k＝k+1；判断：如果k’≤k’，则转到步骤b4；否则转到步骤b8；b8、所有订单指派完毕，停止指派。c、确定配送路线，估算配送成本c1、设定当前配送员序号i＝1，已指派未完成订单的配送成本z＝0；c2、判断：如果配送员序号i≤n，则转到步骤c3，否则转到步骤c5；c3、判断：如果配送员i没有已指派尚未完成的订单，则令zi＝0，转到步骤c4，否则估算配送员i的配送成本zi：c31、假定指派给配送员i的订单为ki＝1,2,…,ki，令di＝{配送员i要配送订单的所有商家位置}＝{lski|ki＝1,2,…,ki}，di’＝φ，φ为空集，位置变量li为配送员i的当前位置，zi＝0，当前时刻为t；c32、计算di中距离li最近的位置dmin，令int()表示上取整，t＝t+ti，li＝dmin；c33、判断：如果dmin为某订单ki的商家位置lski，则令同时用订单ki对应的客户位置lcki取代di中的dmin，tkis＝t，zi＝zi+ti×uc；否则dmin为某订单的客户位置，则同时将dmin从di中移除，即di＝di-{dmin}，tkit＝t，zi＝zi+ti×uc+max{tkit-ltk,0}×dc；c34、判断：如果di≠φ(空集)，则转到步骤c32；否则di’中元素的顺序即为配送顺序，转到步骤c4；c4、令z＝z+zi，i＝i+1，转到步骤c2；c5、停止计算，输出每个配送员i的最优配送路线di’和总的配送成本z。与现有技术相比，本发明具有以下有益效果：1、本发明对外卖订单数据进行预处理时考虑了配送时间、延迟成本等因素外卖订单数据包含商家、客户位置、订单时刻、订单期望配送时间要求等多指标因素，为了完成对配送员的智能快速指派和配送路线快速生成，本发明预处理过程中综合考虑配送员的当前位置、配送员到达商家及客户的时刻，预估配送员的平均配送速度、单位时间配送成本、超出指定配送时间的延迟单位时间成本等因素，并计算获得所有商家、客户的距离，减少指派、路线选取环节的计算量。2、本发明对外卖订单进行智能快速指派提高外卖订单的指派效率为避免出现个别配送员订单特别多而其他配送员空闲的情况，本发明为配送员设置订单容量约束，同时订单指派时优先指派空闲配送员；并依据订单生成时间的顺序指派配送员，避免出现个别订单由于与其他订单距离较远而长时间未被配送的情况。依据单一商家或客户位置进行指派，易于出现先到达客户但尚未到商家取货的情况，鉴于此，本发明为订单指派配送员时，同时考虑商家和客户的位置，只有二者距离都很近的订单才会指派给同一个配送员。3、本发明利用外卖配送需先去商家取货后去客户送货的思想快速选取配送路线传统路线优化问题应用于外卖配送时会受以下三个方面的制约：1)多数路线优化求解算法都需要给定配送中心，车辆从配送中心出发最终回到配送中心的闭环配送路线，而外卖配送的商家位置和数量都是动态需求，且配送路线不是闭环结构；2)多数路线优化求解算法由于是np问题，都采用启发式算法求解，耗费时间长，而o2o外卖平台的订单数据量非常大，要求快速给出建议路线，无法完成多次访问订单数据的任务；3)传统算法即使能实现同时送取货的任务，但所有送的货都来自于固定配送中心，所有取得货都要送到固定配送中心，而外卖配送所有的外卖都需要从随机、动态的商家取货、配送给动态、随机的客户。因此，本发明利用先到商家、后到客户的思想选取路线可以消除外卖配送的条件制约，直接依据配送员到待取餐商家和已取餐客户的距离进行判断，无须固定配送中心或商家位置、无须多次访问数据、无须建立复杂模型即可快速完成配送路线选取过程。4、本发明的方法包括三个过程：一个外卖订单数据预处理过程、一个快速生成外卖订单智能指派过程和依据已指派订单确定配送路线的过程；利用外卖订单预处理完成对动态时间、配送员位置与容量约束及配送与延迟单位成本等参数的初始化，对待指派订单按照其与已指派订单的距离智能选择配送员，利用外卖配送必先到商家取货、后向客户配送的思想为每个配送员快速选择配送路线，并估算配送成本，为调度员提供调度依据。附图说明本发明共有附图3张，其中：图1是o2o外卖平台智能调度与路线优化流程图。图2是订单初始关系结构图。图3是订单最终配送路线图。具体实施方式下面参考附图，详细描述本发明提出的o2o外卖平台智能调度与路线优化方法。如图1所示，本发明包括三个阶段：1、对外卖订单数据进行预处理；2、快速生成外卖订单智能指派模型；3、确定配送路线，估算配送成本。下面以具体例子来说明本发明的实施过程。假设现有待指派订单5个，配送员3个，已指派未完成订单3个，各订单通过gps获取商家和客户的位置，详见表1，表1中订单的初始结构如图2所示。表1订单情况具体步骤如下：a、对外卖订单数据进行预处理a1、依据当前未配送外卖订单记录，令k＝3为已指派尚未完成配送的外卖订单数，k’＝5为未指派配送员的外卖订单数，则lsk(或lsk’)为第k(或k’)个订单的商家位置，lck(或lck’)为第k(或k’)个订单的客户位置，由于位置主要用于计算距离，而外卖配送的区域范围非常小，用直线距离取代地理空间距离对结果不产生影响；k＝1,2,…,k，k’＝1,2,…,k’；a2、令该配送区域内配送员数为n＝3，xki＝1(或xk’i＝1)表示订单k(或k’)指派给配送员i，为0表示未指派给配送员i；xi(s,t)表示配送员i是否需要走边(s,t)(从s位置直接沿着边(s,t)去t位置)，其中是为1，否为0，边长记为l(s,t)；订单k生效时刻为tk0,订单k的客户希望最迟送达时刻为ltk，配送员到订单k的商家取餐的时刻为tks，配送员把订单k送达客户的时刻为tkt；s,t∈{(k+k’)个订单的商家或客户位置}，i＝1,2,…,n；a3、给定配送员平均配送速度为v＝30km/h(0.5km/m)，单位时间配送成本为uc＝0.2元/m，超出指定配送时间的延迟单位时间成本为dc＝0.2元/m，通过当前配送员的手机gps获取位置数据。计算当前所有k’+k(即11)个外卖订单的所有商家lsk、客户位置lck的边长，边长矩阵l＝(l(s,t))2k×2k，边长实际为两点s(s1,s2)、t(t1,t2)的欧氏距离，如式(1)：由定义可知l(s,t)＝l(t,s)，边长矩阵l为对称矩阵，可表示为上三角或下三角矩阵，具体见表2。b、快速生成外卖订单智能指派模型b1、给定配送员已指派未配送的订单容量约束为q＝5；b2、判断：k’+k＝8<n×q＝3×5，则可以全部指派。b3、将当前所有未指派订单按照订单生成的先后顺序排序，订单序号i越小，表示订单生成越早，应该更优先被指派，假定当前订单已经按照生成顺序排列；设定当前未指派订单序号k’＝1(即订单1’)；k’＝1b4、判断：当前是否有空闲配送员i(i＝1,2,…,n)，当前有空闲配送员3，则将订单k’指派给配送员3，即xk’i＝x1’3＝1，转到b7；b7、当前商品节点序号k’＝k’+1＝2，k＝k+1＝4，k＝4对应订单为订单1’，当前各订单状态下表所示；判断：k’＝2≤k’＝5，则转到步骤b4；订单1231’->42’3’4’5’订单状态配送员1配送员2配送员2配送员3未指派未指派未指派未指派k’＝2b4、判断：当前是否有空闲配送员i(i＝1,2,…,n)，当前没有空闲配送员，则转到b5；b5、计算当前订单k’到所有已指派未完成订单的距离，如式(2)d(k’,k)＝l(lsk’,lsk)+l(lck’,lck),k＝1,2,…,k＝4(2)如d(k’,1)＝l(lsk’,ls1)+l(lck’,lc1)＝1.68+8.91＝10.59；同样，得到d(k’,2)＝11.92，d(k’,3)＝14.23，d(k’,4)＝5.54b6、将d(k’,k)按照距离由小到大的顺序排列，分别为：d(k’,4)＝5.54≤d(k’,1)＝10.59≤d(k’,2)＝11.92≤d(k’,3)＝14.23，对应排序后的订单序号kmin＝1,2,…,k，kmin＝1对应的订单为订单4，kmin＝2对应的订单为订单1，kmin＝3对应的订单为订单2，kmin＝4对应的订单为订单3，之后为订单k’指派配送员：b61：设定当前排序后的订单序号kmin＝1(对应订单4)；b62：订单kmin已指派的配送员为imin(配送员3)，判断：如果配送员imin已指派未完成数转到步骤b64。b64：将k’指定给配送员imin＝3，即xk’3＝1(订单2’指派给了配送员3)。b7、当前商品节点序号k’＝k’+1＝3，k＝k+1＝5，当前各订单状态下表所示；判断：如果k’＝3≤k’＝5，则转到步骤b4；k’＝3b4、判断：当前是否有空闲配送员i(i＝1,2,…,n)，当前没有空闲配送员，则转到b5；b5、计算当前订单k’到所有已指派未完成订单的距离，如式(2)d(k’,k)＝l(lsk’,lsk)+l(lck’,lck),k＝1,2,…,k＝5(2)得到d(k’,1)＝17.75，d(k’,2)＝7.13，d(k’,3)＝15.53，d(k’,4)＝13.87，d(k’,5)＝11.3b6、将d(k’,k)按照距离由小到大的顺序排列，分别为：d(k’,2)＝7.13≤d(k’,5)＝11.3≤d(k’,4)＝13.87≤d(k’,3)＝15.53≤d(k’,1)＝17.75，对应排序后的订单序号kmin＝1,2,…,k，kmin＝1对应的订单为订单2，kmin＝2对应的订单为订单5，kmin＝3对应的订单为订单4，kmin＝4对应的订单为订单3，kmin＝5对应的订单为订单1，之后为订单k’指派配送员：b61：设定当前排序后的订单序号kmin＝1(对应订单2)；b62：订单kmin已指派的配送员为imin(配送员2)，判断：如果配送员imin已指派未完成数转到b64。b64：将k’指定给配送员imin＝2，即xk’2＝1(订单3’指派给了配送员2)。b7、当前商品节点序号k’＝k’+1＝4，k＝k+1＝6，当前各订单状态下表所示；判断：如果k’＝4≤k’＝5，则转到步骤b4；订单1231’->42’->53’->64’5’订单状态配送员1配送员2配送员2配送员3配送员3配送员2未指派未指派k’＝4b4、判断：当前是否有空闲配送员i(i＝1,2,…,n)，当前没有空闲配送员，则转到b5；b5、计算当前订单k’到所有已指派未完成订单的距离，如式(2)d(k’,k)＝l(lsk’,lsk)+l(lck’,lck),k＝1,2,…,k＝6(2)得到d(k’,1)＝11.95,d(k’,2)＝9.85,d(k’,3)＝7.5,d(k’,4)＝5.75,d(k’,5)＝9.21,d(k’,6)＝10.75b6、将d(k’,k)按照距离由小到大的顺序排列，分别为：d(k’,4)＝5.75≤d(k’,3)＝7.5≤d(k’,5)＝9.21≤d(k’,2)＝9.85≤d(k’,6)＝10.75≤d(k’,1)＝11.95，对应排序后的订单序号kmin＝1,2,…,k，kmin＝1对应的订单为订单4，kmin＝2对应的订单为订单3，kmin＝3对应的订单为订单5，kmin＝4对应的订单为订单2，kmin＝5对应的订单为订单6，kmin＝6对应的订单为订单1，之后为订单k’指派配送员：b61：设定当前排序后的订单序号kmin＝1(对应订单4)；b62：订单kmin已指派的配送员为imin(配送员3)，判断：如果配送员imin已指派未完成数转到步骤b64。b64：将k’指定给配送员imin＝3，即xk’3＝1(订单4’指派给了配送员3)。b7、当前商品节点序号k’＝k’+1＝5，k＝k+1＝7，当前各订单状态下表所示；判断：如果k’＝5≤k’＝5，则转到步骤b4；订单1231’->42’->53’->64’->75’订单状态配送员1配送员2配送员2配送员3配送员3配送员2配送员3未指派k’＝5b4、判断：当前是否有空闲配送员i(i＝1,2,…,n)，当前没有空闲配送员，则转到步骤b5；b5、计算当前订单k’到所有已指派未完成订单的距离，如式(2)d(k’,k)＝l(lsk’,lsk)+l(lck’,lck),k＝1,2,…,k＝7(2)得到d(k’,1)＝9.14,d(k’,2)＝6.28,d(k’,3)＝9.8,d(k’,4)＝8.48,d(k’,5)＝7.56,d(k’,6)＝12.3,d(k’,7)＝11.03b6、将d(k’,k)按照距离由小到大的顺序排列，分别为：d(k’,2)＝6.28≤d(k’,5)＝7.56≤d(k’,4)＝8.48≤d(k’,1)＝9.14≤d(k’,3)＝9.8≤d(k’,7)＝11.03≤d(k’,6)＝12.3，对应排序后的订单序号kmin＝1,2,…,k，kmin＝1对应的订单为订单2，kmin＝2对应的订单为订单5，kmin＝3对应的订单为订单4，kmin＝4对应的订单为订单1，kmin＝5对应的订单为订单3，kmin＝6对应的订单为订单7，kmin＝7对应的订单为订单6，之后为订单k’指派配送员：b61：设定当前排序后的订单序号kmin＝1(对应订单2)；b62：订单kmin已指派的配送员为imin(配送员2)，判断：如果配送员imin已指派未完成数转到步骤b64。b64：将k’指定给配送员imin＝2，即xk’2＝1(订单5’指派给了配送员2)。b7、当前商品节点序号k’＝k’+1＝6，k＝k+1＝8，当前各订单状态下表所示；判断：如果k’＝6>k’＝5，则转到步骤b8；订单1231’->42’->53’->64’->75’->8订单状态配送员1配送员2配送员2配送员3配送员3配送员2配送员3配送员2b8、所有订单指派完毕，停止指派。c、确定配送路线，估算配送成本zc1、设定当前配送员序号i＝1，已指派未完成订单的配送成本z＝0；i＝1c2、判断：如果配送员序号i＝1≤n，则转到步骤c3c3、判断：如果配送员i有已指派尚未完成的订单，则估算配送员i的配送成本zi：c31、假定指派给配送员i的订单为ki＝1,2,…,ki，令di＝{配送员i要配送订单的所有商家位置}＝{lski|ki＝1,2,…,ki}，由于只有订单1指派给配送员1，所以di＝{订单1的商家位置ls1}，di’＝φ(空集)，位置变量li为配送员i的当前位置，不失一般性，假定当前位置为(0,0)，zi＝0，当前时刻为t＝12:10；c32、计算di中距离li最近的位置dmin，由于di中只有一个元素，即dmin＝ls1，令(分钟)，t＝t+ti＝12:20，li＝dmin＝ls1；c33、判断：dmin(即ls1)为订单1的商家位置lski，则令同时用订单1对应的客户位置lcki取代di中的dmin，即di＝{lc1}，tkis＝t＝12:20，zi＝zi+ti×uc＝0+10×0.2＝2元；c34、判断：如果di＝{lc1}≠φ(空集)，则转到步骤c32；c32、计算di中距离li(即ls1)最近的位置dmin，由于di中只有一个元素，即dmin＝lc1，令(分钟)，t＝t+ti＝12:20+14＝12:34，li＝dmin＝lc1；c33、判断：dmin为订单1的客户位置lc1，则同时将dmin从di中移除，即di＝di-{dmin}＝φ，tkit＝t＝12:34，zi＝zi+ti×uc+max{tkit-ltk,0}×dc＝2+14×0.2+max{12:34-12:40,0}×0.2＝4.8；c34、判断：由于di＝φ，则di’＝{ls1,lc1}中元素的顺序即为配送顺序，转到步骤c4；c4、令z＝z+zi＝4.8，i＝i+1＝2，转到步骤c2；i＝2c2、判断：如果配送员序号i＝2≤n，则转到步骤c3；c3、判断：如果配送员i有已指派尚未完成的订单，则估算配送员i的配送成本zi：c31、假定指派给配送员i的订单为ki＝1,2,…,ki，令di＝{配送员i要配送订单的所有商家位置}＝{lski|ki＝1,2,…,ki}，由于订单2、3、6、8都指派给配送员2，所以di＝{ls2,ls3,ls6,ls8}，di’＝φ，位置变量li为配送员i的当前位置，不失一般性，假定当前位置为(0,0)，zi＝0，当前时刻为t＝12:10；c32、计算di中距离li最近的位置dmin＝ls8，令(分钟)，t＝t+ti＝12:19，li＝dmin＝ls8；c33、判断：dmin(即ls8)为订单8的商家位置lski，则令同时用订单8对应的客户位置lc8取代di中的dmin，即di＝{ls2,ls3,ls6,lc8}，tkis＝t＝12:19，zi＝zi+ti×uc＝0+9×0.2＝1.8元；c34、判断：由于di＝{ls2,ls3,ls6,lc8}≠φ(空集)，则转到步骤c32；c32、查表2获得di中距离li(即ls8)最近的位置dmin，即dmin＝lc8，令(分钟)，t＝t+ti＝12:19+5＝12:24，li＝dmin＝lc8；c33、判断：dmin为订单8的客户位置lc8，则同时将dmin从di中移除，即di＝di-{dmin}＝{ls2,ls3,ls6}，tkit＝t＝12:24，zi＝zi+ti×uc+max{tkit-ltk,0}×dc＝1.8+5×0.2+max{12:24-12:50,0}×0.2＝2.8；c34、判断：由于di＝{ls2,ls3,ls6}≠φ(空集)，则转到步骤c32；c32、查表2获得di中距离li(即lc8)最近的位置dmin，即dmin＝ls2，令(分钟)，t＝t+ti＝12:24+13＝12:37，li＝dmin＝ls2；c33、判断：dmin(即ls2)为订单2的商家位置lski，则令同时用订单2对应的客户位置lc2取代di中的dmin，即di＝{lc2,ls3,ls6}，tkis＝t＝12:37，zi＝zi+ti×uc＝2.8+13×0.2＝5.4元；c34、判断：由于di＝{lc2,ls3,ls6}≠φ(空集)，则转到步骤c32；c32、查表2获得di中距离li(即ls2)最近的位置dmin，即dmin＝ls6，令(分钟)，t＝t+ti＝12:37+4＝12:41，li＝dmin＝ls6；c33、判断：dmin(即ls6)为订单6的商家位置lski，则令lc8，ls2,ls6}，同时用订单6对应的客户位置lc6取代di中的dmin，即di＝{lc2,ls3,lc6}，tkis＝t＝12:41，zi＝zi+ti×uc＝5.4+4×0.2＝6.2元；c34、判断：由于di＝{lc2,ls3,lc6}≠φ(空集)，则转到步骤c32；c32、查表2获得di中距离li(即ls6)最近的位置dmin，即dmin＝lc6，令(分钟)，t＝t+ti＝12:41+11＝12:52，li＝dmin＝lc6；c33、判断：dmin为订单6的客户位置lc6，则同时将dmin从di中移除，即di＝di-{dmin}＝{lc2,ls3}，tkit＝t＝12:52，zi＝zi+ti×uc+max{tkit-ltk,0}×dc＝6.2+11×0.2+max{12:52-12:50,0}×0.2＝8.8；c34、判断：由于di＝{lc2,ls3}≠φ(空集)，则转到步骤c32；c32、查表2获得di中距离li(即lc6)最近的位置dmin，即dmin＝lc2，令(分钟)，t＝t+ti＝12:52+11＝13:03，li＝dmin＝lc2；c33、判断：dmin为订单2的客户位置lc2，则同时将dmin从di中移除，即di＝di-{dmin}＝{ls3}，tkit＝t＝13:03，zi＝zi+ti×uc+max{tkit-ltk,0}×dc＝8.8+11×0.2+max{13:03-12:40,0}×0.2＝15.6；c34、判断：由于di＝{ls3}≠φ(空集)，则转到步骤c32；c32、查表2获得di中距离li(即lc2)最近的位置dmin，由于di中只有一个元素，即dmin＝ls3，令(分钟)，t＝t+ti＝13:21，li＝dmin＝ls3；c33、判断：dmin(即ls3)为订单3的商家位置lski，则令同时用订单3对应的客户位置lc3取代di中的dmin，即di＝{lc3}，tkis＝t＝13:21，zi＝zi+ti×uc＝15.6+18×0.2＝19.2元；c34、判断：如果di＝{lc3}≠φ(空集)，则转到步骤c32；c32、计算di中距离li(即ls3)最近的位置dmin，由于di中只有一个元素，即dmin＝lc3，令(分钟)，t＝t+ti＝13:21+15＝13:36，li＝dmin＝lc3；c33、判断：dmin为订单3的客户位置lc3，则同时将dmin从di中移除，即di＝di-{dmin}＝φ，tkit＝t＝13:36，zi＝zi+ti×uc+max{tkit-ltk,0}×dc＝19.2+15×0.2+max{13:36-12:40,0}×0.2＝33.4；c34、判断：由于di＝φ，则di’＝{ls8,lc8，ls2,ls6,lc6,lc2,ls3,lc3}中元素的顺序即为配送顺序，转到步骤c4；c4、令z＝z+zi＝4.8+33.4＝38.2，i＝i+1＝3，转到步骤c2；i＝3c2、判断：如果配送员序号i＝3≤n，则转到步骤c3；c3、判断：如果配送员i有已指派尚未完成的订单，则估算配送员i的配送成本zi：c31、假定指派给配送员i的订单为ki＝1,2,…,ki，令di＝{配送员i要配送订单的所有商家位置}＝{lski|ki＝1,2,…,ki}，由于订单4、5、7都指派给配送员3，所以di＝{ls4,ls5,ls7}，di’＝φ，位置变量li为配送员i的当前位置，不失一般性，假定当前位置为(0,0)，zi＝0，当前时刻为t＝12:10；c32、计算di中距离li最近的位置dmin＝ls5，令(分钟)，t＝t+ti＝12:17，li＝dmin＝ls5；c33、判断：dmin(即ls5)为订单5的商家位置lski，则令同时用订单5对应的客户位置lc5取代di中的dmin，即di＝{ls4,lc5,ls7}，tkis＝t＝12:17，zi＝zi+ti×uc＝0+7×0.2＝1.4元；c34、判断：由于di＝{ls4,lc5,ls7}≠φ(空集)，则转到步骤c32；c32、查表2获得di中距离li(即ls5)最近的位置dmin，即dmin＝ls4，令(分钟)，t＝t+ti＝12:17+6＝12:23，li＝dmin＝ls4；c33、判断：dmin(即ls4)为订单4的商家位置lski，则令同时用订单4对应的客户位置lc4取代di中的dmin，即di＝{lc4,lc5,ls7}，tkis＝t＝12:23，zi＝zi+ti×uc＝1.4+6×0.2＝2.6元；c34、判断：由于di＝{lc4,lc5,ls7}≠φ(空集)，则转到步骤c32；c32、查表2获得di中距离li(即ls4)最近的位置dmin，即dmin＝lc4，令(分钟)，t＝t+ti＝12:23+11＝12:34，li＝dmin＝lc4c33、判断：dmin为订单4的客户位置lc4，则同时将dmin从di中移除，即di＝di-{dmin}＝{lc5,ls7}，tkit＝t＝12:34，zi＝zi+ti×uc+max{tkit-ltk,0}×dc＝2.6+11×0.2+max{12:34-12:40,0}×0.2＝4.8；c34、判断：由于di＝{lc5,ls7}≠φ(空集)，则转到步骤c32；c32、查表2获得di中距离li(即lc4)最近的位置dmin，即dmin＝lc5，令(分钟)，t＝t+ti＝12:34+6＝12:40，li＝dmin＝lc5；c33、判断：dmin为订单5的客户位置lc5，则同时将dmin从di中移除，即di＝di-{dmin}＝{ls7}，tkit＝t＝12:40，zi＝zi+ti×uc+max{tkit-ltk,0}×dc＝4.8+6×0.2+max{12:40-12:40,0}×0.2＝6；c34、判断：由于di＝{ls7}≠φ(空集)，则转到步骤c32；c32、查表2获得di中距离li(即lc5)最近的位置dmin，由于di中只有一个元素，即dmin＝ls7，令(分钟)，t＝t+ti＝12:40+12＝12:52，li＝dmin＝ls7；c33、判断：dmin(即ls7)为订单7的商家位置lski，则令di’＝di’∪{dmin}＝{ls5,ls4,lc4,lc5,ls7}，同时用订单对7应的客户位置lc7取代di中的dmin，即di＝{lc7}，tkis＝t＝12:52，zi＝zi+ti×uc＝6+12×0.2＝8.4元；c34、判断：如果di＝{lc7}≠φ(空集)，则转到步骤c32；c32、计算di中距离li(即ls7)最近的位置dmin，由于di中只有一个元素，即dmin＝lc7，令(分钟)，t＝t+ti＝12:52+8＝13:00，li＝dmin＝lc7；c33、判断：dmin为订单7的客户位置lc7，则同时将dmin从di中移除，即di＝di-{dmin}＝φ，tkit＝t＝13:00，zi＝zi+ti×uc+max{tkit-ltk,0}×dc＝8.4+8×0.2+max{13:00-12:50,0}×0.2＝12；c34、判断：由于di＝φ，则di’＝{ls5,ls4,lc4,lc5,ls7,lc7}中元素的顺序即为配送顺序，转到步骤c4；c4、令z＝z+zi＝38.2+12＝50.2，i＝i+1＝4，转到步骤c2；c2、判断：如果配送员序号i＝4>n，则转到步骤c5；c5、停止计算，输出每个配送员i的最优配送路线di’和总的配送成本z：每个配送员i的最优配送路线为di’，分别为：d1’＝{ls1,lc1}，d2’＝{ls8,lc8，ls2,ls6,lc6,lc2,ls3,lc3}，d3’＝{ls5,ls4,lc4,lc5,ls7,lc7}；总的配送成本z＝50.2元，配送路线如图3所示。上面是本发明提出的方法的一种实施方式，但在某些步骤上，可以进行适当改变，以适应具体情况的要求。例如，在第一阶段的步骤a3利用两点位置求边长，可以根据实际条件需要适当调整为空间距离。例如，在第三阶段估算配送成本时，配送员的配送路线选取策略可以适当调整。本发明不局限于本实施例，任何在本发明披露的技术范围内的等同构思或者改变，均列为本发明的保护范围。当前第1页12