基于离散化第一价格和比例分配模型的点击量拍卖机制的制作方法

本发明涉及互联网广告领域，具体来说涉及网站广告区域的一种为广告主分配点击量的机制。

背景技术：

overture(原名goto)在1998年开始了付费推广搜索服务，使广告商们对关键词进行竞价，得到不同的搜索结果排名。在中国，百度竞价广告借鉴了overture公司的“竞价排名”，依托百度搜索技术而为广告主提供搜索排名服务，即所谓的关键词竞价拍卖。关键词顾名思义，就是在类似百度、谷歌这样的搜索引擎的搜索框中输入一个或多个相关词语。它们会返回给用户一个相关的广告列表，如果用户点击链接浏览广告，就会收取相应的广告商在此机制下所应支付的价格。而关于返回的广告列表的先后顺序则是在此机制下根据广告商所提交的价格所做出的排序。这里的机制也就是关于关键词排名所要研究的竞价拍卖机制。

竞价搜索拍卖机制主要有三种：vcg、gfp和gsp。gfp作为最早期的竞价搜索拍卖模型，为overture公司带来了巨大的收益，引得众公司纷纷效仿。但overture公司发现了此机制存在的一个很严重的问题：广告商的报价在长时间的竞价过程中会产生剧烈的波动，成锯齿状，这无疑为收益带来极大的不稳定。gsp机制解决了gfp机制的锯齿状波动问题，但同时也带来了一个新的问题：gsp机制会存在多个局部无怨平衡，且每个广告商的估价不是它的占优策略。

vickrey于1961年提出的，并由clarke于1971年、groves于1973年发展并完善，所命名的vcg拍卖机制是一种有效机制，作为第二价格拍卖的一种扩展形式，通过设计每个广告主的支付规则使每个广告主报告自己的估价为占优策略，从而分配到最优位置，最大化社会福利。vcg机制的一个优势就是其平衡唯一且为纳什均衡、满足激励相容。但一直没被采用是因为此机制的收益并不高，且设计的支付规则比较复杂难为广告商所理解。

以上三种典型的机制都是将广告区域划分为位置(slot)，根据广告主的报价高低为其分配相应的位置，dfca机制主要是根据广告主的支付价和比例分配模型为其分配相应的点击量(每个广告所占的区域越大，所获得的点击量越高，网站根据每个广告主所需分配的点击量为其分配相应的面积)，理论证明dfca机制存在唯一均衡。

技术实现要素：

发明目的：本发明所要解决的技术问题是提供一种基于离散化第一价格和比例分配模型的点击量拍卖机制——dfca机制，为现如今网站的广告区域如何有效分配所提供的解决方案。

技术方案：

基于离散化第一价格和比例分配模型的点击量拍卖机制，包括步骤：

1)网站确定所需拍卖的点击量t，其中，t为网站根据历史记录统计出这块广告区域的点击量；

2)网站设置一个保留价格b，增量参数α和点击量比例分配函数f，其中b＞0,α＞0，保留价格为广告主允许参与拍卖的最低门槛；

其中，pi为广告主i为一次点击的支付价，fi(pi)为广告主i所预分配的点击量占总点击量t的比例；

3)网站获取参与拍卖的广告主n1,n2,...,nn，并通知广告主开始报价；

4)广告主i为一次点击报价bi；

5)网站接受广告主n1,n2,...,nn提交的报价b1,b2,...,bn，其中广告主i的支付价为pi，如果广告主i的报价bi满足bk+bk+1≤bi＜bk+1+bk+2，其中bk＝b(1+α)^k-1，广告主i的支付价pi为bk+1；

6)如果所有广告主的报价都不更新，跳转到步骤8)；否则，网站根据分配函数f:(p1,p2,...,pn)→rⁿ预分配点击量比例，其中广告主i所预分配的点击量为t*fi(pi)；

7)广告主i根据效用函数ui(pi)选择最优支付价并提交报价，跳转到步骤5)，其中，广告主i的效用函数为ui(pi)＝t*fi(pi)*(vi-pi)；

8)网站根据分配函数为每个广告主分配点击量，并根据区域面积和点击量的关系为每个广告主分配相应的区域。

所述广告所占的面积越大，它所吸引的点击量越高。

有益效果：本发明存在唯一的均衡点，且广告主的报价越高，所分配的点击量也越高，所分配的广告区域也越大，有效的利用了社会资源，并且为每个广告主提供他们所期待的点击量。

附图说明

图1为dfca机制的算法流程图。

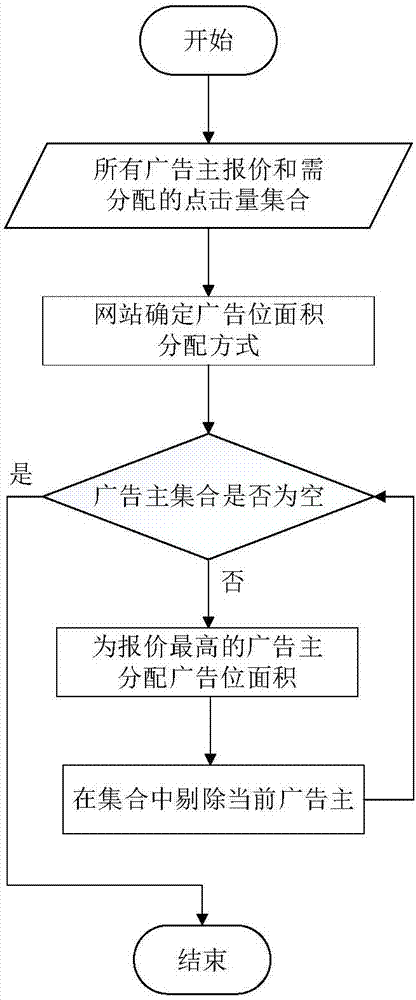
图2为广告主分配广告区域的算法流程图。

具体实施方式

下面结合附图对本发明作更进一步的说明。

本发明机制的具体实施以分配函数为一次函数h(pi)＝pi为例(pi为广告主i为一次点击的支付价)。其中，分配函数可以用一次函数h(pi)＝x*pi+y，二次函数等等定义分配函数(参数x、y和z由网站定义)。

1)网站确定所需拍卖的点击量t(t为网站根据历史记录统计出这块广告区域的点击量)。

2)网站设置一个保留价格b(默认所有广告主的初始报价为保留价格)、增量参数α(b＞0,α＞0，保留价格为广告主允许参与拍卖的最低门槛)和点击量比例分配函数f为

3)网站获取参与拍卖的广告主n1,n2,...,nn，通知广告主开始报价。

4)广告主i为一次点击报价bi。

5)网站接受广告主n1,n2,...,nn提交的报价b1,b2,...,bn，其中广告主i的支付价为pi，如果广告主i的报价bi满足bk+bk+1≤bi＜bk+1+bk+2，其中bk＝b(1+α)^k-1，广告主i的支付价pi为bk+1。

6)如果所有广告主的报价都不更新，跳转到步骤8)；否则，网站根据分配函数f:(p1,p2,...,pn)→rⁿ预分配点击量比例，其中广告主i所预分配的点击量为t*fi(pi)。

广告主i如果评估得出维持当前报价为占优策略，则不更改报价，如果所有广告主都维持当前报价，此机制达到平衡状态，即网站判断的所有广告主的报价都不更新。在此机制下，广告主i的效用函数为

在其策略空间中0＜pi＜vi，ui′＝t*vi*(pi+p-i)^-2，ui″＝t*vi*(-2)*(pi+p-i)^-3易证明ui″＜0，因此其为严格的凹函数。

根据rosen在1965年发表的existenceanduniquenessofequilibriumpointsforconcaven-persongames论文中所证明的定理：在博弈中，如果每个参与者的效用函数在其策略空间内都是严格的凹函数，则该博弈是严格的凹博弈，且每一个n人凹博弈中都存在唯一的一个均衡点。yates在1995年给出了一种标准函数，这种标准函数能够证明通过迭代更新收敛到唯一的不动点。而这种标准函数的意思是在每轮博弈中(其他广告主的报价不改变时)参与者的最优反应唯一，满足该标准函数的博弈具有唯一均衡。

7)广告主i根据效用函数ui(pi)选择支付价其中p-i为其余广告主的支付价。存在一个k值使得bk≤β＜bk+1，最优支付价p满足ui(p)＝max(ui(b),ui(b(1+α))),b＝bk，(如果相同，则选择支付价格高的，在广告主的每一次博弈中，都会选择最优策略)。根据此支付价广告主可以根据事先定义的支付规则选择报价(选择报价时可以选择高价格这样可使排名靠前)，可以看出，这个报价是一个区间，正因为如此才使dfca更易处于平衡之中。提交报价，跳转到步骤5)。

8)网站根据分配函数为每个广告主分配点击量，并根据区域面积和点击量的关系为每个广告主分配相应的区域。假设广告所占的面积(像素点)越大，它所吸引的点击量越高。基于此，通过控制每个广告位置的面积来为其匹配点击量。图2为网站根据每个广告主的点击量为其分配广告位面积的算法流程图。网站根据以前的历史信息得出广告区域和点击量之间的关系，确定广告位面积分配方式，然后根据每个广告主报价的高低依次为他们分配广告区域。

以上所述仅是本发明的优选实施方式，应当指出：对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和润饰，这些改进和润饰也应视为本发明的保护范围。