一种计及非共振传输的中频动响应预示方法与流程

本发明涉及中频动响应预示技术领域，具体涉及一种计及非共振传输的中频动响应预示方法。

背景技术：

复杂系统中可能同时存在较“刚”的部分与较“柔”的部分。在中频段，较“刚”的部分振动波长较长，模态稀疏；较“柔”的部分振动波长较短，存在密集的局部模态。对于该类系统，单一的动响应预示方法不再适用。smeda-sea混合方法能有效解决较“刚”子系统与较“柔”子系统并存时系统的中频动响应预示问题。该方法采用统计模态能量分布分析理论描述较“刚”子系统，采用统计能量分析理论描述较“柔”子系统。

然而，smeda-sea混合方法尚无法考虑非共振模态间的功率传输，即非共振传输。在大阻尼系统中，非共振传输不可忽略，否则会引起分析误差。有必要进一步发展smeda-sea混合方法，计及非共振传输的影响，提高该方法对中频动响应的预示精度。

技术实现要素：

发明目的：针对中频动响应预示方法—smeda-sea混合方法中存在的问题，本发明公开了一种计及非共振传输的中频动响应预示方法，该方法中考虑了非共振模态间的功率传输，能够精确预示较“刚”子系统与较“柔”子系统并存的大阻尼系统的中频动响应。

技术方案：为实现上述目的，本发明采用的技术方案为：

一种计及非共振传输的中频动响应预示方法，包括以下步骤：

步骤1：将系统划分成连续耦合的子系统；

步骤2：计算子系统的模态；

步骤3：计算相邻子系统中模态间的耦合参数；

步骤4：建立系统功率平衡方程，并计算子系统中频动响应。

进一步地，所述步骤1中用虚构的界面将系统划分成连续耦合的子系统，并对子系统在耦合界面上的边界条件进行近似，假定较“刚”子系统在耦合界面上为自由边界，并用位移模态描述该子系统的振动；假定较“柔”子系统在耦合界面上受到固定支撑，并用应力模态描述该子系统的振动。

进一步地，所述步骤2中基于有限元法计算了子系统的模态参数和模态振型。

进一步地，所述步骤3中相邻子系统中模态间的耦合参数由下式计算得到：

其中γmn为位移模态m与应力模态n之间的耦合参数，为位移模态m的第i个分量，s为空间位置，为应力模态n的应力张量，nj为应力模态n所在子系统在耦合边界上单位外法向向量的第j个分量，sc为相邻子系统的耦合界面，mm和mn分别为模态m和模态n的模态质量。

进一步地，所述步骤4中，基于如下系统功率平衡方程可计算得到子系统的中频动响应：

其中ass为ns×ns阶对角矩阵，bcc为nω×nω阶对角矩阵，bsc为ns×nω阶满阵，bcs为nω×ns阶满阵，ns为所有分析频带内较“刚”子系统中的模态总数，nω为分析频带的个数，和es为ns×1阶向量，和为nω×1阶向量。

进一步地，所述对角矩阵ass的第m个对角元素为：

所述对角矩阵bcc的第j个对角元素为：

所述矩阵bsc的第m行第j列元素为：

所述矩阵bcs的第j行第m列元素为：

在式(3-6)中，和分别为位移模态m的阻尼损耗系数和固有频率，ηj为第j个频带δωj内均一化的应力模态的阻尼损耗系数，ωj为第j个频带δωj的中心频率，为第j个频带δωj内应力模态的个数，和为位移模态m和应力模态n间的模态耦合系数。

进一步地，所述位移模态m和应力模态n间的模态耦合系数由下式给出：

其中γmn为模态间的耦合参数，可由式(1)计算得到，和分别为应力模态n的阻尼损耗系数和固有频率。将式(7)中的下标“m”和“n”对调，并将上标“s”和“c”对调，可得到模态耦合系数

进一步地，所述向量es、和由下式给出：

其中为较“刚”子系统中位移模态m的振动能量，为较“柔”子系统在第j个频带δωj内的应力模态的平均振动能量，为较“刚”子系统中位移模态m上的载荷输入功率，为较“柔”子系统在第j个分析频带δωj内的应力模态上的平均载荷输入功率。

有益效果：本发明公开了一种计及非共振传输的中频动响应预示方法，该方法中考虑了非共振模态间的功率传输，能够精确预示较“刚”子系统与较“柔”子系统并存的大阻尼系统的中频动响应。

附图说明

图1是本发明的逻辑流程框图；

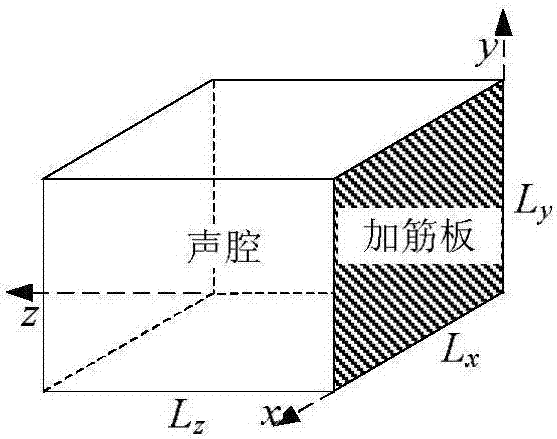
图2是一个加筋板/声腔耦合系统的示意图；

图3是加筋板的有限元模型；

图4是声腔子系统振动能量。

具体实施方式

下面结合附图对本发明作更进一步的说明。

如图1所示为一种计及非共振传输的中频动响应预示方法的逻辑流程框图，主要包括以下步骤：

步骤(1)将系统划分成连续耦合的子系统；用虚构的界面将系统划分成连续耦合的子系统，并对子系统在耦合界面上的边界条件进行近似，假定较“刚”子系统在耦合界面上为自由边界，并用位移模态描述该子系统的振动；假定较“柔”子系统在耦合界面上受到固定支撑，并用应力模态描述该子系统的振动。

步骤(2)计算子系统的模态；具体基于有限元法计算了子系统的模态参数和模态振型。

步骤(3)计算相邻子系统中模态间的耦合参数；具体由下式计算得到：

其中γmn为位移模态m与应力模态n之间的耦合参数，为位移模态m的第i个分量，s为空间位置，为应力模态n的应力张量，nj为应力模态n所在子系统在耦合边界上单位外法向向量的第j个分量，sc为相邻子系统的耦合界面，mm和mn分别为模态m和模态n的模态质量。

步骤(4)中建立系统功率平衡方程，并计算子系统中频动响应；

(4.1)计算位移模态与应力模态间的模态耦合系数：

其中γmn为模态间的耦合参数，可由式(1)计算得到，和分别为位移模态m的阻尼损耗系数和固有频率，和分别为应力模态n的阻尼损耗系数和固有频率。将式(2)中的下标“m”和“n”对调，并将上标“s”和“c”对调，可得到模态耦合系数

(4.2)计算各系数矩阵中的元素，具体包括ns×ns阶对角矩阵ass，nω×nω阶对角矩阵bcc，ns×nω阶满阵bsc，以及nω×ns阶满阵bcs：

ns为所有分析频带内较“刚”子系统中的模态总数，nω为分析频带的个数，ηj为第j个频带δωj内均一化的应力模态的阻尼损耗系数，ωj为第j个频带δωj的中心频率，为第j个频带δωj内应力模态的个数，和为位移模态m和应力模态n间的模态耦合系数。

(4.3)建立系统功率平衡方程：

其中和es为ns×1阶向量，和为nω×1阶向量。

(4.4)计算载荷输入功率：

其中为较“刚”子系统中位移模态m上的载荷输入功率，为较“柔”子系统在第j个分析频带δωj内的应力模态上的平均载荷输入功率。

(4.5)将式(8)代入式(7)，计算得到子系统中频动响应：

其中为较“刚”子系统中位移模态m的振动能量，为较“柔”子系统在第j个频带δωj内的应力模态的平均振动能量。

实施例

以一个加筋板/声腔耦合模型为例，如图2所示。加筋板的边界条件为：四条边上简支，加筋板的有限元模型如图3所示；加筋板的面板的参数由表1给出，筋条的材料参数与面板的材料参数相同，平行于x轴向筋条的尺寸为1m×0.03m×0.005m，间距1/6m，平行于y轴向筋条的尺寸为1m×0.02m×0.005m，间距1/6m。声腔的边界条件为：除与加筋板耦合的面，其余各面为固定边界；声腔的参数由表2给出。

表1加筋板的面板的参数取值

表2声腔的参数取值

在加筋板外表面施加单位完全随机噪声载荷，分别基于传统smeda-sea混合方法和本发明提出的计及非共振传输的smeda-sea混合方法，预示了声腔子系统在各分析频段内的平均模态振动能量，如图4所示。该结果显示，对于该大阻尼加筋板/声腔耦合系统，基于传统的smeda-sea混合方法的预示结果存在误差，而基于本发明提出的计及非共振传输的smeda-sea混合方法能准确预示系统的中频动响应。

本实施例最终取得的效果说明，本发明所提出的方法能有效地解决“刚”子系统与“柔”子系统并存的大阻尼系统的中频动响应预示问题，提高分析的精度。

以上所述仅是本发明的优选实施方式，应当指出：对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和润饰，这些改进和润饰也应视为本发明的保护范围。